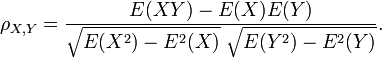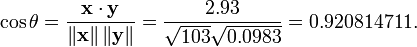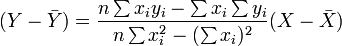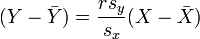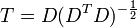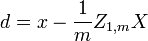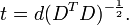Corrélation

Saviez-vous ...

SOS croit que l'éducation donne une meilleure chance dans la vie des enfants dans le monde en développement aussi. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.

Cet article porte sur le coefficient de corrélation entre deux variables. Le terme corrélation peut aussi signifier la corrélation croisée des deux fonctions ou corrélation d'électrons dans des systèmes moléculaires.

Plusieurs ensembles de (x, y) points, le coefficient de corrélation x et y pour chaque ensemble. Notez que la corrélation reflète le caractère bruyant et la direction d'une relation linéaire (rangée du haut), mais pas la pente de cette relation (au milieu), ni de nombreux aspects des relations non linéaires (en bas). NB: le chiffre dans le centre dispose d'une pente de 0 mais dans ce cas, le coefficient de corrélation est définie parce que la variance de Y est zéro.

Dans la théorie des probabilités et statistiques , corrélation, (souvent mesurée comme un coefficient de corrélation), indique la force et la direction d'une relation linéaire entre deux variables aléatoires . Dans l'usage statistique général, la corrélation ou co-relation désigne le départ de deux variables de l'indépendance. Dans ce sens large, il existe plusieurs coefficients, mesurant le degré de corrélation, adaptée à la nature des données.

Un certain nombre de coefficients différents sont utilisés pour différentes situations. Le plus connu est le Pearson coefficient de corrélation produit-moment, qui est obtenu en divisant le covariance des deux variables par le produit de leurs écarts types . Malgré son nom, il a été introduit par Francis Galton.

Le coefficient produit-moment de Pearson

Propriétés mathématiques

Le coefficient de corrélation ρ _{X, Y} entre deux variables aléatoires X et Y avec valeurs attendues μ _X et _Y μ et écarts types σ _X et _Y σ est définie comme:

$\ Rho_ {X, Y} = {\ mathrm {} cov (X, Y) \ over \ sigma_X \ sigma_Y} = {E ((X \ mu_X) (Y \ mu_Y)) \ over \ sigma_X \ sigma_Y} ,$

où E est le opérateur de valeur attendue et cov moyens covariance. Depuis μ _X = E (X), σ _X ² = E (X ²⁾ - ² E (X) et de même pour Y, on peut aussi écrire

$\ Rho_ {X, Y} = \ frac {E (XY) -E (X) E (Y)} {\ sqrt {E (X ^ 2) -E ^ 2 (X)} ~ \ sqrt {E (Y ^ 2) ^ 2 -E (Y)}}.$

La corrélation est définie que si les deux des écarts types sont limitées et deux d'entre eux sont non nuls. Ce est un corollaire de l' inégalité de Cauchy-Schwarz que la corrélation ne peut pas dépasser 1 en valeur absolue .

La corrélation est 1 dans le cas d'une relation linéaire croissante, -1 dans le cas d'une relation linéaire décroissante, et une valeur entre dans tous les autres cas, ce qui indique le degré de dépendance linéaire entre les variables. Plus le coefficient est soit -1 ou 1, plus la corrélation entre les variables.

Si les variables sont indépendant puis la corrélation est égal à 0, mais le contraire ne est pas vrai, parce que le coefficient de corrélation ne détecte que des dépendances linéaires entre les deux variables. Voici un exemple: Supposons que la variable aléatoire X est réparti uniformément sur l'intervalle -1 à 1, et Y = X ^2. Alors Y est complètement déterminée par X, de sorte que X et Y dépendent, mais leur corrélation est égal à zéro; ils sont décorrélées. Toutefois, dans le cas particulier où X et Y représentent conjointement normale, non corrélation est équivalent à l'indépendance.

Une corrélation entre deux variables est dilué en présence d'erreur de mesure autour des estimations de l'un ou les deux variables, auquel cas disattenuation fournit un coefficient plus précis.

Interprétation géométrique de corrélation

Le coefficient de corrélation peut également être considéré comme le cosinus de l' angle entre les deux vecteurs d'échantillons tirés des deux variables aléatoires.

Attention: Cette méthode fonctionne uniquement avec des données centrées, ce est à dire, les données qui ont été décalées de la moyenne de l'échantillon de manière à avoir une moyenne de zéro. Certains praticiens préfèrent une (non-conforme Pearson) coefficient de corrélation décentré. Voir l'exemple ci-dessous pour une comparaison.

A titre d'exemple, supposons que cinq pays sont trouvés d'avoir des produits nationaux bruts de 1, 2, 3, 5 et 8 milliards de dollars, respectivement. Supposons que ces cinq mêmes pays (dans le même ordre) sont trouvés d'avoir 11%, 12%, 13%, 15%, et 18% la pauvreté. Ensuite, laissez x et y être commandés vecteurs 5 éléments contenant les données ci-dessus: x = (1, 2, 3, 5, 8) et y = (0,11, 0,12, 0,13, 0,15, 0,18).

Par la procédure habituelle pour trouver l'angle entre deux vecteurs (voir point produit), le coefficient de corrélation est décentré:

$\ Cos \ theta = \ frac {\ gras {x} \ cdot \ gras {y}} {\ left \ | \ gras {x} \ right \ | \ left \ | \ gras {y} \ right \ |} = \ frac {2,93} {\ sqrt {103} \ sqrt {}} = 0,0983 0,920814711.$

Notez que les données ci-dessus ont été délibérément choisis pour être parfaitement corrélés: y = 0,10 + 0,01 x. Le coefficient de corrélation de Pearson doit donc être exactement un. Centrage des données (décalage x par E (x) = 3,8 et y par E (y) = 0,138) rendements x = (-2,8, -1,8, -0,8, 1,2, 4,2) et y = (-0,028, -0,018, -0,008, 0,012, 0,042), à partir de laquelle

$\ Cos \ theta = \ frac {\ gras {x} \ cdot \ gras {y}} {\ left \ | \ gras {x} \ right \ | \ left \ | \ gras {y} \ right \ |} = \ frac {0,308} {\ sqrt {30,8} \ sqrt {}} = 0,00308 1 = \ {xy} rho_,$

comme prévu.

Motivation pour la forme du coefficient de corrélation

Une autre motivation pour la corrélation vient d'inspecter la méthode d'une simple régression linéaire . Comme ci-dessus, X est le vecteur des variables indépendantes, 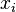$x_i$ Et Y des variables dépendantes, 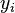$y_i$ Et une relation linéaire simple entre X et Y est recherchée, par une méthode des moindres carrés sur l'estimation de Y:

$\ Y = X \ beta + \ varepsilon. \,$

Ensuite, l'équation de la droite des moindres carrés peut être dérivé à être de la forme:

$(Y - \ bar {Y}) = \ frac {n \ sum x_iy_i- \ sum x_i \ sum y_i} {n \ sum x_i ^ 2 - (\ sum x_i) ^ 2} (X - \ bar {X})$

qui peuvent être réorganisés sous la forme:

$(Y - \ bar {Y}) = \ frac {} {r s_y s_x} (X \ bar {X})$

où r a la forme familière mentionné ci-dessus: 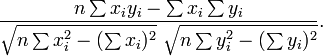$\ Frac {n \ sum x_iy_i- \ sum x_i \ sum y_i} {\ sqrt {n \ sum x_i ^ 2 - (\ sum x_i) ^ 2} ~ \ sqrt {n \ sum y_i ^ 2 - (\ sum y_i) ^ 2}}.$

Interprétation de la taille d'une corrélation

Corrélation	Négatif	Positif
Petit	-0,3 À -0,1	0,1 à 0,3
Moyen	-0,5 À -0,3	0,3 à 0,5
Grand	-1,0 À -0,5	0,5 à 1,0

Plusieurs auteurs ont proposé des lignes directrices pour l'interprétation d'un coefficient de corrélation. Cohen (1988), par exemple, a suggéré les interprétations suivantes des corrélations dans la recherche psychologique, dans le tableau sur la droite.

Comme Cohen lui-même a observé, toutefois, tous ces critères sont en quelque sorte arbitraire et ne doivent pas être observés de manière trop stricte. En effet, l'interprétation d'un coefficient de corrélation dépend du contexte et des objectifs. Une corrélation de 0,9 peut être très faible si l'on vérifie une loi physique en utilisant des instruments de haute qualité, mais peut être considéré comme très élevé dans les sciences sociales, où il peut y avoir une plus grande contribution des facteurs de complication.

Le long de cette veine, il est important de rappeler que «grande» et «petite» ne devrait pas être pris comme synonymes de «bon» et «mauvais» en termes de déterminer qu'une corrélation est d'une certaine taille. Par exemple, une corrélation de 1,0 ou -1,0 indique que les deux variables sont analysées calibrage modulo équivalent. Scientifiquement, cela signifie plus fréquemment le résultat trivial qu'un fracassant une. Par exemple, considérez la découverte d'une corrélation de 1,0 entre le nombre de pieds de hauteur un groupe de personnes sont et le nombre de pouces du fond de leurs pieds au dessus de leurs têtes.

Les coefficients de corrélation non paramétriques

Le coefficient de corrélation de Pearson est un statistique paramétrique et lorsque les distributions ne sont pas normaux, il peut être moins utile que des méthodes de corrélation non paramétriques, tels que Chi-carré, Pointez corrélation bisériale, La ρ de Spearman et Le τ de Kendall. Ils sont un peu moins puissant que les méthodes paramétriques si les hypothèses sous-jacentes ce dernier sont remplies, mais sont moins susceptibles de donner des résultats faussés lorsque les hypothèses échouent.

Autres mesures de dépendance entre les variables aléatoires

Pour obtenir une mesure de plus de dépendances générales dans les données (également non linéaire), il est préférable d'utiliser la rapport de corrélation qui est capable de détecter presque toute dépendance fonctionnelle, ou la basée sur l'entropie information mutuelle / corrélation totale qui est capable de détecter des dépendances même plus générales. Ces derniers sont parfois appelés mesures de corrélation multi-moments, par rapport à ceux qui considèrent seulement 2e instant (par paires ou quadratique) la dépendance.

Le polychoric corrélation est une autre corrélation appliquée aux données ordinales qui vise à estimer la corrélation entre les variables latentes théorisés.

Copules et corrélation

L'information fournie par un coefficient de corrélation ne est pas suffisant pour définir la structure de dépendance entre les variables aléatoires; pour capturer pleinement, nous devons envisager une copule entre eux. Le coefficient de corrélation définit complètement la structure de dépendance que dans des cas très particuliers, par exemple lorsque le fonctions de répartition sont les distributions normales multivariées. Dans le cas des distributions elliptiques elle caractérise les (hyper) ellipses de densité égale, cependant, il ne caractérise pas complètement la structure de dépendance (par exemple, les degrés de liberté de l'un multivariée t de distribution déterminent le niveau de dépendance de queue).

matrices de corrélation

La matrice de corrélation des variables aléatoires X ₁ n, ..., X _n est la matrice n × n dont i, j est entrée corr (X _i, X _j). Si les mesures de corrélation sont utilisés coefficients produit-moment, la matrice de corrélation est le même que le matrice de covariance des variables aléatoires normalisées X _i / SD (X _i) pour i = 1, ..., n. Par conséquent, il est nécessairement un matrice semi-définie positive.

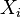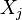La matrice de corrélation est symétrique car la corrélation entre $X_i$ et $X_j$ est la même que la corrélation entre 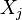$X_j$ et $X_i$ .

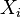Retrait corrélation

Il est toujours possible de supprimer la corrélation entre les variables aléatoires de moyenne nulle avec une transformation linéaire, même si la relation entre les variables est non linéaire. Supposons un vecteur de variables aléatoires n est échantillonné m fois. Soit X une matrice où 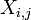$X_ {i, j}$ est le j e variable de l'échantillon i. Laisser 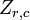$Z_ {r, c}$ être un r par la matrice de c avec chaque élément 1. Alors D est les données transformées de sorte que chaque variable aléatoire a moyenne nulle, et T est les données transformées de façon toutes les variables ont une moyenne nulle, de variance unité, et de zéro corrélation avec toutes les autres variables. Les variables transformées seront pas corrélées, même si elles peuvent ne pas être indépendante.

$D = X - \ frac {1} {m} Z_ {m, m} X$

$T = D (D ^ T D) ^ {- \ frac {1} {2}}$

où un exposant de -1/2 représente la racine carrée de la matrice inverse d'une matrice. La matrice de covariance de T sera la matrice identité. Si un nouvel échantillon de données x est un vecteur ligne de n éléments, la même transformation peut être appliquée à x pour obtenir les vecteurs transformés D et T:

$d = x - \ frac {1} {m} Z_ {1, m} X$

$t = d (D ^ T D) ^ {- \ frac {1} {2}}.$

Idées fausses sur la corrélation

Corrélation et causalité

Le dicton classique qui " corrélation ne implique pas causalité "signifie que la corrélation ne peut être valablement utilisée pour déduire une relation de causalité entre les variables. Cette maxime ne devrait pas être interprété comme signifiant que les corrélations ne peuvent pas révéler des relations causales. Toutefois, les causes sous-jacentes de la corrélation, le cas échéant, peut être indirecte et inconnus. Par conséquent, l'établissement d'une corrélation entre deux variables ne est pas une condition suffisante pour établir une relation causale (dans les deux sens).

Voici un exemple simple: temps chaud peut provoquer les achats de criminalité et de glaces. Par conséquent la criminalité est en corrélation avec les achats glaces. Mais le crime ne provoque pas achats glaces et les achats glaces ne causent pas de crime.

Une corrélation entre l'âge et la hauteur chez les enfants est assez causalement transparent, mais une corrélation entre l'humeur et la santé dans la population est moins. Amélioration de l'humeur ne conduisent à une meilleure santé? Ou est bonne avance de santé à la bonne humeur? Ou ne un autre facteur sous-tendent les deux? Ou est-ce une pure coïncidence? En d'autres termes, une corrélation peut être considéré comme une preuve d'un lien de causalité possible, mais ne peut pas indiquer quelle est la relation de cause à effet, le cas échéant, pourrait être.

Corrélation et linéarité

Quatre ensembles de données avec le même corrélation de 0,81

Bien que la corrélation de Pearson indique la force d'une relation linéaire entre deux variables, sa valeur seule peut ne pas suffire pour évaluer cette relation, en particulier dans le cas où l'hypothèse de normalité est incorrect.

L'image sur la droite affiche nuages de points Quartet d'Anscombe, un ensemble de quatre paires différentes de variables créées par Francis Anscombe. Les quatre $y$ variables ont la même moyenne (7,5), l'écart-type (4,12), la corrélation (0,81) et la ligne de régression ( $y = 3 + 0.5x$ ). Cependant, comme on peut le voir sur les emplacements, la distribution des variables est très différente. La première (en haut à gauche) semble être distribué normalement, et correspond à ce que l'on pourrait se attendre lorsque l'on considère deux variables corrélées et après l'hypothèse de normalité. Le second (en haut à droite) ne est pas distribuée normalement; alors une relation évidente entre les deux variables peut être observé, il ne est pas linéaire, et le coefficient de corrélation de Pearson ne est pas pertinent. Dans le troisième cas (en bas à gauche), la relation linéaire est parfait, sauf une aberrante qui exerce une influence suffisante pour abaisser le coefficient de corrélation de 1 à 0,81. Enfin, l'exemple quatrième (en bas à droite) montre un autre exemple où une valeur aberrante est suffisante pour produire un coefficient de corrélation élevé, même si la relation entre les deux variables ne est pas linéaire.

Ces exemples montrent que le coefficient de corrélation, comme une statistique sommaire, ne peut pas remplacer l'examen individuel des données.

Le calcul de corrélation avec précision en une seule passe

L'algorithme suivant (en pseudo) calculera Corrélation de Pearson avec une bonne stabilité numérique.

 sum_sq_x = 0 = 0 sum_sq_y sum_coproduct = 0 mean_x = x [1] mean_y = y [1] for i in 2 à N: balayage = (i - 1,0) / i delta_x = x [i] - mean_x delta_y = y [i ] - mean_y sum_sq_x + = delta_x * * delta_x balayage sum_sq_y + = delta_y * * delta_y balayage sum_coproduct + = delta_x * * delta_y balayage mean_x + = delta_x / i mean_y + = delta_y / i pop_sd_x = sqrt (sum_sq_x / N) pop_sd_y = sqrt (sum_sq_y / N) = cov_x_y sum_coproduct / N = corrélation cov_x_y / (pop_sd_x * pop_sd_y)

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Correlation_and_dependence&oldid=199055311 "