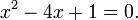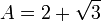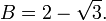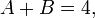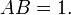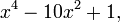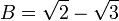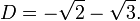La théorie de Galois

Évariste Galois (1811-1832)

En mathématiques , plus précisément dans l'algèbre abstraite , la théorie de Galois, nommé d'après Évariste Galois, fournit une connexion entre théorie des champs et la théorie des groupes . En utilisant la théorie de Galois, certains problèmes en théorie des champs peuvent être réduites à la théorie des groupes, qui est en quelque sorte plus simple et mieux compris.

Originaire de Galois utilisé groupes de permutation pour décrire comment les différents racines d'une donnée polynôme équation sont liés les uns aux autres. L'approche moderne de la théorie de Galois, développé par Richard Dedekind, Leopold Kronecker et Emil Artin, entre autres, consiste à étudier automorphismes de extensions de terrain.

En outre abstraction de la théorie de Galois est réalisée par la théorie de connexions de Galois.

Application aux problèmes classiques

La naissance de la théorie de Galois a été motivée par la question suivante, dont la réponse est connue sous le nom Théorème Abel-Ruffini.

"Pourquoi est-il pas de formule pour les racines d'un cinquième (ou ultérieure) degré équation polynomiale en termes de coefficients du polynôme, en utilisant uniquement les opérations habituelles algébriques (addition, soustraction, multiplication, division) et application des radicaux (racines carrées , racines cubiques, etc.)? "

La théorie de Galois ne fournit pas seulement une belle réponse à cette question, il explique également en détail pourquoi il est possible de résoudre des équations de degré quatre ou moins de la manière ci-dessus, et pourquoi leurs solutions prennent la forme qu'ils font. En outre, il donne un moyen conceptuellement claires, pratiques et souvent, de dire quand une certaine équation particulière de degré supérieur peut être résolu de cette manière.

La théorie de Galois donne aussi un aperçu clair des questions concernant les problèmes en règle et au compas construction. Il donne une caractérisation élégante des rapports de longueurs qui peuvent être construits avec cette méthode. Avec cela, il devient relativement facile de répondre à ces problèmes classiques de la géométrie que

«réguliers Quels polygones sont polygones constructibles? "

"Pourquoi est-il pas possible de trisecter tous les angles? "

Histoire

La théorie de Galois origine dans l'étude des fonctions symétriques - les coefficients d'un polynôme sont (au signe près) le polynômes symétriques élémentaires dans les racines. Par exemple, (x - a) (x - b) = x ² - (a + b) + x ab, où 1, a + b et ab sont des polynômes de degré 0 élémentaires, une et deux à deux variables.

Ce fut d'abord formalisée par le mathématicien français du 16e siècle François Viète, dans Les formules de Viète, pour le cas de racines réelles positives. De l'avis du mathématicien britannique du 18e siècle Charles Hutton, l'expression de coefficients d'un polynôme en termes de racines (non seulement pour les racines positives) a été entendu par le mathématicien français du 17e siècle Albert Girard; Hutton écrit:

... [Girard était] la première personne qui a compris la doctrine générale de la formation des coefficients des puissances de la somme des racines et de leurs produits. Il fut le premier qui a découvert les règles pour sommer les pouvoirs des racines de toute équation.

Dans cette veine, le discriminante est une fonction symétrique dans les racines qui reflète les propriétés des racines - elle est nulle si et seulement si le polynôme a une racine multiple, et pour les polynômes quadratiques et cubiques il est positif si et seulement si toutes les racines sont réels et distinct, et négatif si et seulement se il existe une paire de racines complexes conjuguées distinctes. Voir Discriminante: nature des racines pour plus de détails.

Le cube a d'abord été en partie résolu par la 15 / mathématicien italien du 16ème siècle Scipione del Ferro, qui ne ont cependant pas publier ses résultats; cette méthode seulement résolu une des trois classes, comme les autres personnes impliquées de prendre racines carrées des nombres négatifs et les nombres complexes ne étaient pas connus à l'époque. Cette solution a ensuite été redécouvert en 1535 par Niccolò Fontana Tartaglia, qui a partagé avec Jérôme Cardan, lui demandant de ne pas publier. Cardano ensuite étendu cela aux deux autres cas, en utilisant des racines carrées de négatifs comme des étapes intermédiaires; voir les détails au La méthode de Cardan. Après la découverte du travail de Ferro, il a estimé que la méthode de Tartaglia ne était plus un secret, et donc il a publié son solution complète dans son 1545 Ars Magna. Son élève Lodovico Ferrari résolu le polynôme quartique, quelle solution Cardano également inclus dans Ars Magna.

Une autre étape a été la 1770 papier Réflexions sur la résolution des équations algébrique par le mathématicien français-italien Joseph Louis Lagrange , dans son mode de Résolvantes de Lagrange, où il a analysé la solution de Cardano et Ferrarri des cubiques et quartiques en les considérant en termes de permutations des racines, qui a donné un polynôme auxiliaire de degré inférieur, fournissant une compréhension unifiée des solutions et de jeter les bases de la théorie des groupes et de Galois théorie. Fondamentalement, cependant, qu'il ne considérait pas la composition de permutations. La méthode de Lagrange ne pas se étendre aux équations quintiques ou plus, parce que la résolvante avait degré plus élevé.

Le quintique était presque prouvé ne pas avoir de solutions générales de radicaux par Paolo Ruffini en 1799 , dont l'idée maîtresse était d'utiliser groupes de permutation, et pas seulement une seule permutation. Sa solution contenait un écart, qui Cauchy considéré comme mineur, mais cela n'a pas été patché jusqu'à ce que le travail de mathématicien norvégien Niels Henrik Abel, qui a publié une preuve en 1824, établissant ainsi la Théorème Abel-Ruffini.

Alors que Ruffini et Abel établi que les quintique générale ne pouvait être résolu, certains quintiques particuliers peuvent être résolus, tels que (x - 1) ^5, et le critère précis par lequel un polynôme quintique ou plus donné pourrait être jugée solvable ou non a été donnée par Évariste Galois, qui a montré que si un polynôme est solvable ou non était équivalente à savoir si ou non le groupe de permutation de ses racines - en termes modernes, son Groupe de Galois - eu une certaine structure - en termes modernes, si oui ou non ce était une groupe résoluble. Ce groupe était toujours solvable pour les polynômes de degré quatre ou moins, mais pas toujours aussi pour les polynômes de degré cinq ans et plus, ce qui explique pourquoi il n'y a pas de solution générale au plus haut degré.

L'approche du groupe de permutation à la théorie de Galois

Etant donné un polynôme, il se peut que certaines des racines sont reliées par diverses équations algébriques. Par exemple, il se peut que pour deux des racines, disent A et B, que A ² + ³ = 5 B 7. L'idée centrale de la théorie de Galois est de considérer ces permutations (ou réarrangements) des racines ayant la propriété toute équation algébrique satisfait par les racines est toujours satisfait après les racines ont été permutées. Une condition importante est que nous nous limitons à des équations algébriques dont les coefficients sont des nombres rationnels . (On pourrait au lieu de spécifier un certain domaine dans lequel les coefficients doit mentir, mais, pour les exemples simples ci-dessous, nous allons nous limiter au domaine des nombres rationnels.)

Ces permutations forment ensemble un groupe de permutation, aussi appelé le Groupe de Galois du polynôme (sur les nombres rationnels). Pour illustrer ce point, considérons les exemples suivants:

Premier exemple - une équation quadratique

Prenons l' équation quadratique

En utilisant la formule quadratique , nous constatons que les deux racines sont

Exemples d'équations algébriques satisfaits par A et B comprennent

et

Évidemment, dans l'une de ces équations, si nous échangeons A et B, nous obtenons une autre déclaration vrai. Par exemple, l'équation A + B = 4 devient tout simplement B + A = 4. En outre, il est vrai, mais beaucoup moins évident que cela est possible pour chaque équation algébrique rationnelle coefficients satisfaits par les racines A et B; cela nécessite de prouver la théorie de polynômes symétriques.

Nous concluons que le groupe de Galois du polynôme x ² - 4 x + 1 est constitué de deux permutations: l' identité permutation qui laisse intacte A et B, et la transposition permutation qui échange A et B. Il se agit d'un groupe cyclique d'ordre deux, et par conséquent isomorphe à Z / 2 Z.

On pourrait objecter que A et B sont liés par une autre équation algébrique,

qui ne reste pas vrai lorsque A et B sont échangées. Cependant, cette équation ne nous concerne pas, parce qu'il n'a pas coefficients rationnels; en particulier, est pas rationnel.

Un débat similaire se applique à tout polynôme ax ² + bx + c quadratique, où a, b et c sont des nombres rationnels.

• Si le polynôme a une seule racine, par exemple x ^2-4 x + 4 = (x-2) ^2, puis le groupe de Galois est sans importance; autrement dit, il ne contient que la permutation identité.
• Si elle a deux racines rationnelles distinctes, par exemple x ^2-3 x + 2 = (x -2) (x-1), le groupe de Galois est encore négligeable.
• Si elle a deux racines irrationnelles (y compris le cas où les racines sont complexe ), puis le groupe de Galois contient deux permutations, comme dans l'exemple ci-dessus.

Deuxième exemple

Considérons le polynôme

qui peut également se écrire

Nous tenons à décrire le groupe de Galois de ce polynôme, à nouveau sur le champ de nombres rationnels . Le polynôme a quatre racines:

Il ya 24 façons possibles de permuter ces quatre racines, mais pas tous de ces permutations sont membres du groupe de Galois. Les membres du groupe de Galois doivent préserver toute équation algébrique à coefficients rationnels impliquant A, B, C et D. Une telle équation est

A + D = 0.

Toutefois, étant donné

,

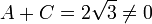la permutation

(A, B, C, D) → (A, B, D, C)

ne est pas autorisé (parce qu'il transforme l'équation valable A + D = 0 dans l'équation invalide A + C = 0).

Une autre équation que les racines satisfont est

Cela exclure d'autres, tels que les permutations

(A, B, C, D) → (A, C, B, D).

Poursuivant dans cette voie, nous constatons que les seules permutations (satisfaisant les deux équations simultanément) restants sont

(A, B, C, D) → (A, B, C, D)

(A, B, C, D) → (C, D, A, B)

(A, B, C, D) → (B, A, D, C)

(A, B, C, D) → (D, C, B, A),

et le groupe de Galois est isomorphe au Groupe de Klein.

L'approche moderne en théorie des champs

Dans l'approche moderne, on part d'un champ extension L / K (lire: L sur K), et examine le groupe de champ automorphismes de L / K (ceux-ci sont mappages α: L → L avec α (x) = x pour tout x dans K). Voir l'article sur groupes de Galois pour de plus amples explications et des exemples.

La liaison entre les deux approches est la suivante. Les coefficients du polynôme en question devraient être choisis dans le domaine de base K. Le champ supérieur L devrait être le champ obtenu en adjoignant les racines du polynôme en question dans le champ base. Toute permutation des racines qui respecte les équations algébriques comme décrit ci-dessus donne lieu à une automorphismes de L / K, et vice versa.

Dans le premier exemple ci-dessus, nous avons étudié l'extension Q (√3) / Q, où Q est le domaine des nombres rationnels , et Q (√3) est le champ obtenu à partir de Q en adjoignant √3. Dans le deuxième exemple, nous avons étudié l'extension Q (A, B, C, D) / Q.

Il ya plusieurs avantages à l'approche moderne à l'approche du groupe de permutation.

• Il permet une déclaration beaucoup plus simple de la théorème fondamental de la théorie de Galois.
• L'utilisation de champs de base autres que Q est crucial dans de nombreux domaines des mathématiques. Par exemple, dans théorie algébrique des nombres, on fait souvent en utilisant la théorie de Galois les champs numériques, champs finis ou champs locaux que le champ de base.
• Il permet d'étudier plus facilement les extensions infinies. Encore une fois ce qui est important en théorie algébrique des nombres, où, par exemple on discute souvent le groupe absolue de Galois de Q, définie comme le groupe de Galois de K / Q où K est un clôture algébrique de Q.
• Il permet de tenir compte des extensions inséparables. Ce problème ne se pose pas dans le cadre classique, car il a toujours été implicitement supposé que l'arithmétique a eu lieu en caractéristique zéro, mais caractéristique non nulle se pose fréquemment dans la théorie des nombres et géométrie algébrique.
• Il supprime la dépendance plutôt artificielle sur la chasse racines de polynômes. Ce est, différents polynômes peuvent produire les mêmes champs d'extension, et l'approche moderne reconnaît le lien entre ces polynômes.

Groupes résolubles et la solution par les radicaux

La notion de groupe résoluble dans la théorie des groupes permet de déterminer si un polynôme est soluble dans les radicaux, selon que son groupe de Galois a la propriété de solvabilité. En substance, chaque champ extension L / K correspond à une groupe de facteurs dans un suite de composition du groupe de Galois. Si un groupe de facteur de la série composition est cyclique d'ordre n, puis si l'extension du champ correspondant est une extension d'un champ contenant un racine primitive de l'unité, il est alors une extension radicale, et les éléments de L peut alors être exprimé en utilisant le n ième racine d'un élément de K.

Si tous les groupes de facteurs dans sa série de composition sont cycliques, le groupe de Galois est appelé résoluble, et tous les éléments du champ correspondant peut être trouvée en prenant plusieurs reprises racines, des produits et des sommes d'éléments du champ de base (généralement Q) .

L'un des grands triomphes de la théorie de Galois était la preuve que pour tout n> 4, il existe des polynômes de degré n qui ne sont pas résoluble par les radicaux-le Théorème Abel-Ruffini. Cela est dû au fait que, pour n> 4, le groupe symétrique S _n contient un simple, non cyclique, sous-groupe normal.

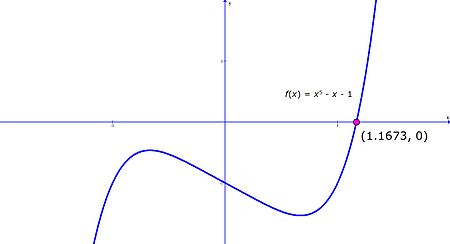
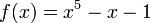Le polynôme . La vraie racine solitaire = 1,1673 ... est algébrique, mais pas exprimable que les radicaux. Les quatre autres racines sont les nombres complexes .

Un exemple quintique non-résoluble

Van der Waerden cite le polynôme 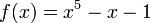. Par le Racine évidente qu'il n'a pas de zéros rationnels. Elle ne dispose pas des facteurs linéaires modulo 2 ou 3.

a la factorisation modulo 2. Cela signifie que son groupe de Galois modulo 2 est cyclique d'ordre six.

a aucun facteur quadratique modulo 3. Ainsi son groupe de Galois modulo 3 est d'ordre 5.

Nous savons qu'un groupe de Galois modulo un premier est isomorphe à un sous-groupe du groupe de Galois sur les rationnels. Un groupe de permutation sur les cinq objets avec des opérations de commandes 6 et 5 doit être le groupe symétrique 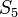, Qui doit être le groupe de Galois de . Ce est l'un des exemples les plus simples d'un quintique polynôme non solvable. Serge Lang dit que Artin aimait cet exemple.

Le problème inverse de Galois

Tous les groupes finis ne produisent que des groupes de Galois. Il est facile de construire des extensions de champ avec ne importe quel groupe fini comme groupe de Galois donné, tant que l'on ne spécifie pas également la champ de terrain.

Pour cela, choisissez un champ K et un groupe fini G. Théorème de Cayley dit que G est (à isomorphisme près) un sous-groupe de la groupe symétrique S sur les éléments de G. Choisissez indéterminées {x} _α, un pour chaque élément α de G, et jouxtent les à K pour obtenir le champ F = K ({x} _α). Contenue dans F est le champ L de symétrie fonctions rationnelles dans le {x} _α. Le groupe de Galois de F / L est S, par un résultat de base de Emil Artin. G agit sur F par restriction d'action de S. Si le champ fixe de cette action est M, puis, par la théorème fondamental de la théorie de Galois, le groupe de Galois de F / M est G.

Ce est un problème ouvert à prouver l'existence d'une extension du champ du champ rationnelle Q avec un groupe fini donné que le groupe de Galois. Hilbert a joué un rôle dans la résolution du problème pour tous les groupes symétriques et en alternance. Igor Shafarevich prouvé que chaque groupe fini résoluble est le groupe de Galois de certains extension de Q. Diverses personnes ont résolu l'inverse de Galois problème pour non-abélienne sélectionnée groupes simples. Existence de solutions a été montré pour tous, mais peut-être un ( Groupe de Mathieu M ₂₃₎ des 26 groupes simples sporadiques. Il ya même un polynôme à coefficients entiers dont le groupe de Galois est le Groupe Monstre.