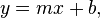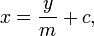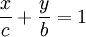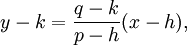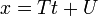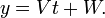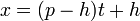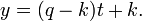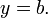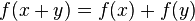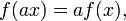Équation linéaire

Renseignements généraux

SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

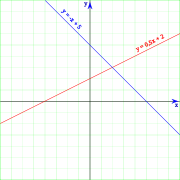
échantillon de graphique d'équations linéaires

Une équation linéaire est un équation algébrique dans laquelle chaque terme est soit un constante ou le produit d'une constante multipliée par la puissance d'un premier variable. Une telle équation est équivalente à assimiler une polynôme du premier degré à zéro. Ces équations sont appelés «linéaire», car ils représentent des lignes droites en coordonnées cartésiennes . Une forme courante d'une équation linéaire dans les deux variables $x$ et $y$ est

$y = mx + b. \,$

Sous cette forme, la constante $m$ déterminera le pente ou gradient de la ligne; et le terme constant $b$ permettra de déterminer le moment où la ligne traverse l'axe des y. Équations impliquant des termes tels que x ², y ^1/3, et xy sont non linéaire.

Formulaires pour 2D équations linéaires

Équations linéaires complexes, telles que celles ci-dessus, peuvent être réécrites en utilisant les lois de l'algèbre élémentaire en plusieurs formes plus simples. Dans ce qui suit x, y et t sont des variables; autres lettres représentent constantes (non précisées mais les numéros fixes).

Forme générale

$Ax + By + C = 0, \,$

où A et B ne sont pas tous deux égaux à zéro. L'équation est généralement écrite de telle sorte que A ≥ 0, par convention. Le graphique de l'équation est une ligne droite , et chaque ligne droite peut être représentée par une équation dans le formulaire ci-dessus. Si A ne est pas nul, alors le x ordonnée à l'origine, ce est le x - coordonnée du point où la courbe croise la axe des x (y vaut zéro), est - C / A. Si B est différent de zéro, alors l'ordonnée à l'origine, ce est le -Coordonner y du point où la courbe croise la axe des y (x est égal à zéro), est - C / B, et la pente de la ligne est - A / B.

Forme standard

$Ax + By = C, \,$

où A, B, et C sont des nombres entiers dont le plus grand facteur commun est 1, A et B ne sont pas tous deux égaux à zéro et A est non-négatif (et si A = 0, alors B doit être positif). Le formulaire standard peut être convertie à la forme générale, mais pas toujours à toutes les autres formes si A ou B est zéro.

Forme d'une pente

Y axe formule

$y = mx + b, \,$

où m est la pente de la droite et b est l'ordonnée à l'origine de y, qui est la y -Coordonner du point où la ligne coupe l'axe des y. Ceci peut être vu en laissant $x = 0$ , Ce qui donne immédiatement $y = b$ .

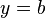Formule axe X

$x = \ frac {y} {} m + c, \,$

où m est la pente de la droite et c est l'ordonnée à l'origine x, où x est le -Coordonner du point où la ligne coupe l'axe x. Ceci peut être vu en laissant 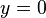$y = 0$ , Ce qui donne immédiatement $x = c$ .

Point-forme pente

$y - y_1 = m \ cdot (x - x 1),$

où m est la pente de la droite et (x _1, y ₁₎ est ne importe quel point sur la ligne. Les formulaires points-pente et la pente d'interception sont facilement interchangeables.

La forme de point pente exprime le fait que la différence de coordonnée y entre deux points sur une ligne (ce est-à 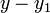$y - y_1$ ) Est proportionnelle à la différence de la coordonnée x (ce est- 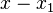$x - x_1$ ). La constante de proportionnalité est m (la pente de la droite).

Intercept forme

$\ Frac {x} {c} + \ frac {y} {b} = 1$

où c et b doivent être non nulle. Le graphique de l'équation a ordonnée à l'origine x c et y b ordonnée à l'origine. La forme d'interception peut être converti en la forme standard en réglant A = 1 / c, B = 1 / b et C = 1.

Sous forme de deux points

$y - k = \ frac {q - k} {p - h} (x - h),$

où p ≠ h. Le graphique passe par les points (h, k) et (p, q), et a une pente m = (q - k) / (p - h).

Forme paramétrique

$x = T t + U \,$

$y = V t + W. \,$

Deux équations simultanées en termes d'un paramètre variable t, avec une pente m = V / T, x ordonnée à l'origine (VU - WT) / V et ordonnée à l'origine (WT - VU) / T.

Cela peut aussi être liée à la forme de deux points, où T = P - H, U = H, V = q - k, et W = k:

$x = (p - h) t + h \,$

$y =. (q - k) t + k \,$

Dans ce cas t varie de 0 au point (h, k) à 1 au point (p, q), avec des valeurs de t entre 0 et 1 fournissant interpolation et d'autres valeurs de t fournir extrapolation.

Forme normale

$y \ sin \ phi + x \ cos \ phi - p = 0, \,$

où φ est l'angle d'inclinaison de la normale et p est la longueur de la normale. La normale est définie comme étant le segment le plus court entre la ligne en question et l'origine. Forme normale peut être dérivée de forme générale en divisant tous les coefficients par $\ Frac {| C |} {- C} \ sqrt {A ^ 2 + B ^ 2}$ . Cette forme aussi appelé Hesse formulaire standard, nommé d'après un mathématicien allemand Ludwig Otto Hesse.

Cas particuliers

$y = b. \,$

Ce est un cas particulier de la forme standard où A = 0 et B = 1, ou de la forme d'une pente où la pente M = 0. Le graphique est une ligne horizontale avec ordonnée à l'origine égale à b. Il n'y a pas x ordonnée à l'origine, à moins que b = 0, auquel cas la courbe de la ligne est la axe des x, et ainsi de tout nombre réel x est une ordonnée à l'origine.

$x = c. \,$

Ce est un cas particulier de la forme standard où A = 1 et B = 0. Le graphique est une ligne verticale avec x ordonnée à l'origine égale à c. La pente ne est pas définie. Il ne est pas ordonnée à l'origine, à moins que c = 0, auquel cas la courbe de la ligne est l'axe des y, et de façon tout nombre réel est une ordonnée à l'origine.

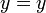$y = y \$ et $x = x. \,$

Dans ce cas, toutes les variables et les constantes ont annulé, laissant un trivialement vraie déclaration. L'équation originale, donc, serait appelé identité et une ne envisageraient pas normalement son graphe (ce serait la toute-Plane xy). Un exemple est de 2 x 4 + y = 2 (x + y) 2. Les deux expressions de chaque côté du signe égal sont toujours égaux, peu importe ce que les valeurs sont utilisées pour x et y.

$e = f. \,$

Dans les situations où la manipulation algébrique conduit à un énoncé tel que 1 = 0, alors l'équation originale est appelé incompatibles, ce qui signifie qu'il ne est pas vrai pour toutes les valeurs de x et y (ie son graphe serait le vide set) Un exemple serait 3 x + 2 = 3 x - 5.

Connexion avec des fonctions linéaires et opérateurs

Dans toutes les formes nommés ci-dessus (en supposant que le graphique ne est pas une ligne verticale), la variable y représente une fonction de x, et le graphe de cette fonction est le graphe de l'équation.

Dans le cas particulier que la ligne traverse l'origine, si l'équation linéaire est écrit sous la forme y = f (x) alors f a les propriétés:

$f (x + y) = f (x) + f (y) \,$

$f (a x) = a f (x), \,$

où a est ne importe quel scalaire. Une fonction qui satisfait à ces propriétés est appelé une fonction linéaire, ou plus généralement un linéaire. Cette propriété rend équations linéaires particulièrement facile à résoudre et de raisonner sur.

Équations linéaires se produisent avec une grande régularité en mathématiques appliquées . Alors qu'ils se posent tout naturellement lors de la modélisation de nombreux phénomènes, ils sont particulièrement utiles car beaucoup équations non linéaires peuvent être réduites à des équations linéaires en supposant que les quantités d'intérêt varient dans une faible mesure seulement d'un état "de fond".

Équations linéaires à plus de deux variables

Une équation linéaire peut impliquer plus de deux variables. L'équation linéaire générale n variables est:

$a_1 x_1 + a_2 x_2 + \ cdots + a_n x_n = b.$

Sous cette forme, a _1, a _2, ..., c _n sont des coefficients, x _1, x _2, ..., x _n sont des variables, et b est égal à la constante. Lorsqu'il se agit de trois ou moins de variables, il est fréquent de remplacer x ₁ avec juste x, x _2, avec y et z x ₃ avec, le cas échéant.

Une telle équation représentera une (n-1) de dimension hyperplan de dimension n dans l'espace euclidien (par exemple, un plan dans l'espace 3).

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Linear_equation&oldid=198721570 "