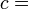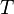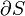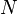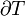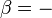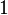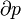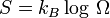Troisième loi de la thermodynamique

Thermodynamique
Le moteur thermique classique Carnot
Branches Classique · statistiques · Chimique Equilibrium / Non-équilibre
Lois Zeroth · Première · Deuxième Troisième ·
Systèmes État: Équation d'état Idéal gaz · Gaz réel Phase de matière · Équilibre Contrôle du volume · Instruments Processus: Isobarique · Isochore · Isothermal Adiabatique · Isentropique · Isenthalpique Quasistatique · Polytropic Libre dilatation Réversibilité · Irréversibilité Endoreversibility Cycles: Les moteurs thermiques · Pompes à chaleur L'efficacité thermique
Propriétés système diagrammes de propriété Propriétés intensives et extensives Fonctions d'Etat: Température / entropie ( intro. ) † Pression / Volume † Potentiel chimique / Particule non. † († Variables conjuguées) La qualité de vapeur Propriétés réduits fonctions du processus: Travail · Heat
Propriétés des matériaux Capacité thermique spécifique Compressibilité Dilatation thermique base de données de propriété
Équations Le théorème de Carnot · Clausius théorème · Relation fondamentale · Loi des gaz parfaits · Relations de Maxwell · Relations réciproques Onsager · Équations thermodynamiques de Bridgman Table des équations thermodynamiques
Potentiels L'énergie gratuite · Entropie gratuit L'énergie interne Enthalpie Énergie libre Énergie libre de Gibbs
Histoire et culture Philosophie: Entropie et l'heure · Entropie et de la vie Cliquet brownien Le démon de Maxwell la mort de chaleur paradoxe Le paradoxe de Loschmidt Synergetics Histoire: Général · Chaleur · Entropy · lois de gaz Mouvement perpétuel Théories: Théorie du calorique · Vis viva Théorie de la chaleur Équivalent mécanique de la chaleur La force motrice Publications: " Un expérimentale ... Enquête sur l'Heat " " Sur l'équilibre des substances hétérogènes " "Réflexions sur la Motive Power of Fire " Échéanciers de: Thermodynamique · Les moteurs thermiques Art: Surface thermodynamique de Maxwell Éducation: Entropie dispersion d'énergie
Les scientifiques Bernoulli · Carnot · Clapeyron · Clausius · von Helmholtz · Carathéodory · Pierre Duhem · Gibbs · Joule · Maxwell · von Mayer · Onsager · Rankine · Smeaton · Stahl · Thompson · Kelvin · Waterson

La troisième loi de la thermodynamique est une loi statistique de la nature concernant l'entropie :

L'entropie d'un cristal parfait se rapproche de zéro lorsque la température se approche de zéro absolu.

Pour d'autres matériaux, la entropie résiduelle ne est pas nécessairement zéro,

Histoire

La troisième loi a été élaboré par le chimiste Walther Nernst pendant les années 1906-1912, et est donc souvent considéré comme le théorème de Nernst ou le postulat de Nernst. La troisième loi de la thermodynamique affirme que la entropie d'un système à zéro absolu est une constante bien définie. En effet, un système à température nulle existe dans son état de base, de sorte que son entropie est déterminée que par la la dégénérescence de l'état du sol. Cela signifie que «il est impossible de ne importe quel mode opératoire, quelle que soit idéalisée, afin de réduire ne importe quel système à la température de zéro absolu dans un nombre fini d'opérations".

Une version alternative de la troisième loi de la thermodynamique comme indiqué par Gilbert N. Lewis et Merle Randall en 1923:

Si l'entropie de chaque élément dans un état (parfait) cristallin être considéré comme nul au zéro absolu de température, chaque substance a une entropie positif finie; mais au zéro absolu de température l'entropie peut devenir nulle, et ne deviennent ainsi dans le cas de substances cristallines parfaites.

Cette version Etats non seulement Δ S atteindront zéro à 0 kelvins, mais S se seront également atteindre le niveau zéro aussi longtemps que le cristal a un état fondamental avec une seule configuration. Des cristaux se forment des défauts qui provoque une entropie résiduelle. Cette entropie résiduelle disparaît lorsque les barrières cinétiques à la transition vers un état du sol sont surmontés.

Avec le développement de la mécanique statistique , la troisième loi de la thermodynamique (comme les autres lois) a changé à partir d'une loi fondamentale (justifiée par des expériences) à un droit dérivé (dérivé de lois encore plus de base). La loi de base à partir de laquelle il est principalement dérivé est la définition statistique de la mécanique de l'entropie pour un grand système:

où S est l'entropie, k _B est la Constante de Boltzmann, et 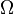est le nombre de micro-compatibles avec la configuration macroscopique.

Vue d'ensemble

En termes simples, la troisième loi stipule que l'entropie d'un cristal parfait se rapproche de zéro lorsque la température se approche de zéro absolu. Cette loi fournit un point de référence pour la détermination absolue de l'entropie. L'entropie déterminée par rapport à ce point est l'entropie absolue.

L'entropie d'un treillis de cristal parfait tel que défini par le théorème de Nernst est zéro (à condition que son état fondamental est unique, de sorte que ln (1) k = 0).

Un exemple d'un système qui ne présente pas un état de base unique est une demi-entier contenant tours, pour lesquels retournement temporel symétrie donne deux états fondamentaux dégénérés (une entropie de ln (2) k, qui est négligeable à l'échelle macroscopique). Certains présentent des systèmes cristallins frustration géométrique, où la structure du réseau cristallin empêche l'émergence d'un état fondamental unique. L'état fondamental de l'hélium (sauf sous pression) reste liquide.

En outre, des lunettes et des solutions solides conservent grande entropie au 0K, parce qu'ils sont de grandes collections de près états dégénérés, dans lequel ils sont piégés hors d'équilibre. Un autre exemple d'un solide avec de nombreux Etats sol près dégénérés, piégés hors d'équilibre, est la glace Ih, qui a «Trouble à protons".

Pour la troisième loi d'appliquer strictement, les moments magnétiques d'un cristal parfaitement ordonné doivent eux-mêmes être parfaitement ordonné; En effet, du point de vue entropique, cela peut être considéré comme faisant partie de la définition de «cristal parfait". Seulement ferromagnétique, antiferromagnétique, et matériaux diamagnétiques peuvent satisfaire à cette condition. Les matériaux qui restent à 0K paramagnétique, en revanche, peuvent avoir de nombreux états fondamentaux presque dégénérés (par exemple, dans un verre de spin), ou peut conserver le désordre dynamique ( liquide de spin ).