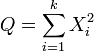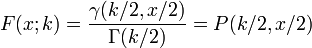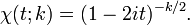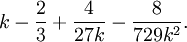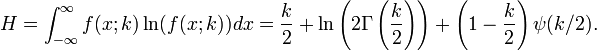Distribución Chi-cuadrado
Sabías ...
Esta selección Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Está disponible como una descarga intranet. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?
La función de densidad de probabilidad 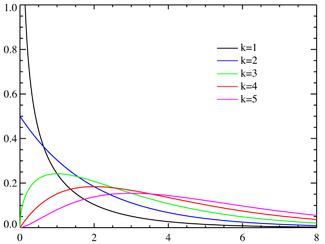 | |
Función de distribución acumulativa  | |
| Parámetros | 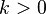 grados de libertad grados de libertad |
|---|---|
| Apoyo |  |
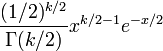 | |
| CDF | 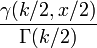 |
| Significar | 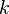 |
| Mediana | aproximadamente 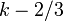 |
| Modo |  si si 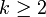 |
| Desacuerdo | 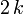 |
| Oblicuidad | 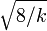 |
| Ex. curtosis | 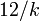 |
| Entropía | 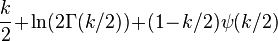 |
| MGF | 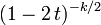 para para  |
| CF | 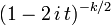 |
En teoría de la probabilidad y estadística , la distribución de chi-cuadrado (también chi-cuadrado o 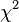 distribución) es uno de los más utilizados teóricos de distribuciones de probabilidad en estadística inferencial, por ejemplo, en pruebas de significación estadística. Es útil porque, bajo supuestos razonables, cantidades calculadas pueden ser fácilmente demostrado tener distribuciones que se aproximan a la distribución chi-cuadrado si el hipótesis nula es verdadera.
distribución) es uno de los más utilizados teóricos de distribuciones de probabilidad en estadística inferencial, por ejemplo, en pruebas de significación estadística. Es útil porque, bajo supuestos razonables, cantidades calculadas pueden ser fácilmente demostrado tener distribuciones que se aproximan a la distribución chi-cuadrado si el hipótesis nula es verdadera.
Si 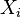 son k independientes, distribuidas normalmente variables aleatorias con media 0 y varianza 1, entonces la variable aleatoria
son k independientes, distribuidas normalmente variables aleatorias con media 0 y varianza 1, entonces la variable aleatoria
se distribuye de acuerdo a la distribución de chi-cuadrado. Esto se suele escribir
La distribución chi-cuadrado tiene un parámetro: 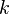 - Un número entero positivo que especifica el número de grados de libertad (es decir, el número de
- Un número entero positivo que especifica el número de grados de libertad (es decir, el número de 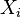 )
)
La distribución chi-cuadrado es un caso especial de la distribución gamma.
Las situaciones más conocidas en el que se utilizan la distribución chi-cuadrado son el común pruebas de chi-cuadrado para bondad de ajuste de una distribución observada a una teórica, y de la independencia de los dos criterios de clasificación de datos cualitativos. Sin embargo, muchas otras pruebas estadísticas conducen a un uso de esta distribución. Un ejemplo es Análisis de Friedman de la varianza por rangos.
Características
La función de densidad de probabilidad
La función de densidad de probabilidad de la distribución chi-cuadrado es
donde  denota la Función Gamma, que toma valores particulares en las semi-enteros.
denota la Función Gamma, que toma valores particulares en las semi-enteros.
Función de distribución acumulativa
Su función de distribución acumulativa es:
donde 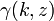 es el menor función gamma incompleta y
es el menor función gamma incompleta y  es el función gamma regularizada.
es el función gamma regularizada.
Las tablas de esta distribución - por lo general en su forma acumulativa - están ampliamente disponibles y la función se incluye en muchos hojas de cálculo y todo paquetes estadísticos.
Función característica
La función característica de la distribución Chi-cuadrado es
Propiedades
La distribución chi-cuadrado tiene numerosas aplicaciones en inferencia estadística , por ejemplo en pruebas de chi-cuadrado y en la estimación de varianzas . Entra en el problema de estimar la media de una población normalmente distribuida y el problema de la estimación de la pendiente de una regresión línea a través de su papel en la distribución t de Student . Entra en todo análisis de los problemas de la varianza a través de su papel en el F-distribución, que es la distribución de la relación de dos chi-cuadrado independientes variables aleatorias divididas por sus respectivos grados de libertad.
Aproximación normal
Si 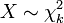 , Entonces como
, Entonces como 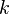 tiende a infinito, la distribución de
tiende a infinito, la distribución de 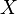 tiende a la normalidad. Sin embargo, la tendencia es lenta (la asimetría es
tiende a la normalidad. Sin embargo, la tendencia es lenta (la asimetría es 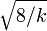 y el exceso de curtosis es
y el exceso de curtosis es 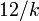 ) Y dos transformaciones se consideran comúnmente, cada uno de los cuales se aproxima a la normalidad más rápido que
) Y dos transformaciones se consideran comúnmente, cada uno de los cuales se aproxima a la normalidad más rápido que 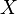 sí:
sí:
Fisher mostró empíricamente que 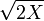 es aproximadamente una distribución normal con media
es aproximadamente una distribución normal con media  y la varianza unidad. Es posible llegar al mismo resultado normal aproximación mediante el uso de momento coincidente. Para ver esto, considere la media y la varianza de una variable aleatoria distribuida-Chi
y la varianza unidad. Es posible llegar al mismo resultado normal aproximación mediante el uso de momento coincidente. Para ver esto, considere la media y la varianza de una variable aleatoria distribuida-Chi  , Que se dan por
, Que se dan por 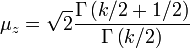 y
y 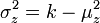 , Donde
, Donde 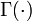 es la función Gamma. La relación particular de las funciones gamma en
es la función Gamma. La relación particular de las funciones gamma en 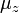 tiene la siguiente expansión de la serie :
tiene la siguiente expansión de la serie :
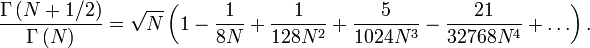 Cuando
Cuando  , Esta relación se puede aproximar como sigue:
, Esta relación se puede aproximar como sigue: 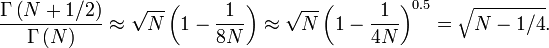
Entonces, simple momento resultados coincidentes en la siguiente aproximación de 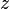 :
: 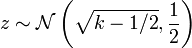 , De la cual se deduce que
, De la cual se deduce que  .
.
Wilson y Hilferty mostraron en 1931 que ![\ Sqrt [3] {X / k}](../../images/185/18595.png) es aproximadamente una distribución normal con media
es aproximadamente una distribución normal con media 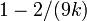 y la varianza
y la varianza 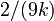 .
.
La valor esperado de una variable aleatoria que tiene una distribución chi-cuadrado con 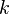 grados de libertad es
grados de libertad es 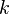 y la varianza es
y la varianza es 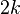 . La mediana está dada aproximadamente por
. La mediana está dada aproximadamente por
Tenga en cuenta que 2 grados de libertad de plomo a una distribución exponencial .
Información entropía
La información de entropía viene dada por
donde 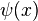 es el Función digamma.
es el Función digamma.
Distribuciones Relacionados
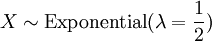 es una distribución exponencial si
es una distribución exponencial si  (Con 2 grados de libertad).
(Con 2 grados de libertad). 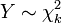 es una distribución chi-cuadrado si
es una distribución chi-cuadrado si  para
para  independiente que se distribuye normalmente .
independiente que se distribuye normalmente . - Si el
 disponer de medios distintos de cero, entonces
disponer de medios distintos de cero, entonces  se extrae de una distribución chi-cuadrado no central.
se extrae de una distribución chi-cuadrado no central. - La distribución de chi-cuadrado
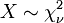 es un caso especial de la distribución gamma, en ese
es un caso especial de la distribución gamma, en ese 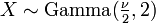 .
.  es una F-distribución si
es una F-distribución si  donde
donde 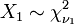 y
y  son independientes con sus respectivos grados de libertad.
son independientes con sus respectivos grados de libertad. 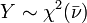 es una distribución chi-cuadrado si
es una distribución chi-cuadrado si 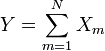 donde
donde 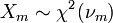 son independientes y
son independientes y 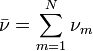 .
. - si
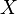 se distribuye chi-cuadrado, entonces
se distribuye chi-cuadrado, entonces  es chi distribuida.
es chi distribuida. - En particular, si
 (Chi-cuadrado con 2 grados de libertad), a continuación,
(Chi-cuadrado con 2 grados de libertad), a continuación,  es Distribución de Rayleigh.
es Distribución de Rayleigh. - si
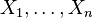 son iid
son iid 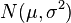 variables aleatorias , entonces
variables aleatorias , entonces 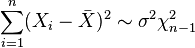 donde
donde 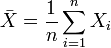 .
. - si
 , A continuación,
, A continuación, 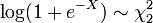
| Nombre | Estadística |
|---|---|
| distribución chi-cuadrado | 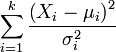 |
| no central chi-cuadrado de distribución | 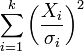 |
| distribución chi |  |
| distribución chi no central |  |