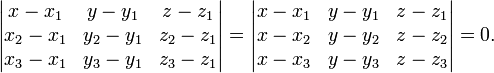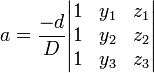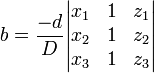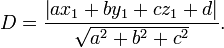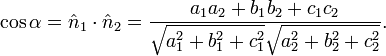Avión (geometría)
Antecedentes
SOS Children produjo este sitio web para las escuelas, así como este sitio web video sobre África . SOS Children ha cuidado de niños en África durante cuarenta años. ¿Puedes ayudar a su trabajo en África ?
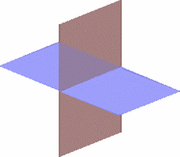
En matemáticas , un avión es un bidimensional colector o superficie que es perfectamente plana. Informalmente, se puede considerar como una hoja infinitamente vasto y infinitesimalmente delgada orientada en algunos espacio. Formalmente, es una espacio afín de dimensión dos.
Cuando se trabaja en el espacio euclidiano de dos dimensiones, se utiliza el artículo definido, el avión, para referirse a todo el espacio. Muchas de las tareas fundamentales en la geometría , la trigonometría , y la representación gráfica se llevan a cabo en el espacio de dos dimensiones, o en otras palabras, en el plano. Una gran cantidad de las matemáticas puede ser y ha sido realizado en el plano, en especial en las áreas de la geometría , trigonometría , la teoría de grafos y gráfica.
Geometría euclidiana
En el espacio euclidiano de un avión es una superficie de tal manera que, dado cualquier dos distintos puntos de la superficie, la superficie también contiene la única línea recta que pasa por esos puntos.
La estructura fundamental de dos de tales aviones siempre será el mismo. En matemáticas esto se describe como la equivalencia topológica . De manera informal, sin embargo, significa que cualquiera de los dos aviones tienen el mismo aspecto.
Un avión se puede determinar claramente por cualquiera de los siguientes (conjuntos de) los objetos:
- tres puntos no colineales (es decir, no puesto en la misma línea )
- una línea y un punto no en la línea
- dos líneas con un punto de intersección
- dos líneas paralelas
Planes incrustados en R 3
Esta sección se ocupa específicamente de aviones incrustados en tres dimensiones: en concreto, en ℝ 3.
Propiedades
En el espacio euclidiano tridimensional, podemos aprovechar los siguientes hechos que no tienen en dimensiones superiores:
- Dos planos son paralelos o que se cruzan en una línea.
- Una línea es ya sea paralelo a un plano o corta que en un solo punto o está contenida en el plano.
- Dos líneas perpendicular al mismo plano debe ser paralelos entre sí.
- Dos planos perpendiculares a la misma línea deben ser paralelos entre sí.
Definir un avión con un punto y un vector normal
En un espacio tridimensional, otra forma importante de la definición de un plano es mediante la especificación de un punto y una vector normal al plano.
Dejar 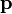 ser el punto que queremos estar en el plano, y deje
ser el punto que queremos estar en el plano, y deje 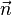 ser un vector normal al plano distinto de cero. El plano deseado es el conjunto de todos los puntos
ser un vector normal al plano distinto de cero. El plano deseado es el conjunto de todos los puntos  de tal manera que
de tal manera que 
Si escribimos  ,
,  y d como el producto escalar
y d como el producto escalar  , Entonces el plano
, Entonces el plano 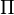 se determina por la condición
se determina por la condición 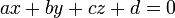 , Donde a, b, c y d son números reales y a, b, y c no son todos cero.
, Donde a, b, c y d son números reales y a, b, y c no son todos cero.
Alternativamente, un plano se puede describir paramétricamente como el conjunto de todos los puntos de la forma  donde s y t rango sobre todos los números reales, y
donde s y t rango sobre todos los números reales, y 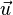 ,
, 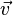 y
y 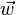 son dados los vectores que definen el plano.
son dados los vectores que definen el plano. 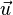 puntos desde el origen hasta un punto arbitrario en el avión, y
puntos desde el origen hasta un punto arbitrario en el avión, y 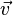 y
y 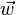 puede ser visualizado como a partir de las
puede ser visualizado como a partir de las 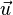 y apuntando en diferentes direcciones a lo largo del plano.
y apuntando en diferentes direcciones a lo largo del plano. 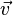 y
y 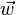 puede, pero no tiene que ser perpendicular (pero no pueden ser alineados).
puede, pero no tiene que ser perpendicular (pero no pueden ser alineados).
Definir un plano que pasa por tres puntos
- El plano que pasa por tres puntos
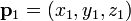 ,
, 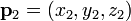 y
y 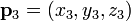 se puede definir como el conjunto de todos los puntos (x, y, z) que satisfacen las siguientes determinantes ecuaciones:
se puede definir como el conjunto de todos los puntos (x, y, z) que satisfacen las siguientes determinantes ecuaciones:
- Para describir el avión como una ecuación en la forma
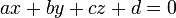 , Resolver el siguiente sistema de ecuaciones:
, Resolver el siguiente sistema de ecuaciones:
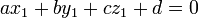
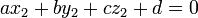
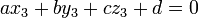 .
.
Este sistema se puede resolver utilizando De Regla y manipulaciones de matrices básicas Cramer. Dejar  . Luego,
. Luego,
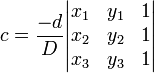 .
.
Estas ecuaciones son paramétricas en d. Configuración d igual a cualquier número distinto de cero y sustituyéndola en estas ecuaciones producirá un conjunto de soluciones.
- Este plano también puede ser descrita por el "punto y un vector normal" receta anterior.
Un vector normal adecuada viene dada por el producto cruzado  y el punto
y el punto 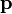 se pueden tomar para ser cualquiera de los puntos dados
se pueden tomar para ser cualquiera de los puntos dados  o
o  .
.
Distancia de un punto a un plano
Para un avión 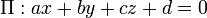 y un punto
y un punto 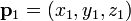 no necesariamente coincide con el plano, la distancia más corta desde
no necesariamente coincide con el plano, la distancia más corta desde 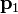 al plano es
al plano es
Resulta que 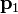 se encuentra en el plano si y sólo si D = 0.
se encuentra en el plano si y sólo si D = 0.
Si  lo que significa que a, b y c se normalizan entonces la ecuación se convierte en
lo que significa que a, b y c se normalizan entonces la ecuación se convierte en
Línea de intersección entre dos planos
Planos que se intersectan Dadas descritos por 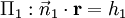 y
y 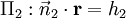 , La línea de intersección es perpendicular tanto
, La línea de intersección es perpendicular tanto 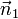 y
y  y por lo tanto paralela a
y por lo tanto paralela a 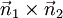 .
.
Si suponemos además que 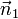 y
y  son ortonormal entonces el punto más cercano en la línea de intersección con el origen es
son ortonormal entonces el punto más cercano en la línea de intersección con el origen es 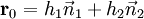 .
.
Ángulo diedro
Dadas dos planos que se cortan descritos por  y
y 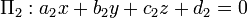 , La ángulo diedro entre ellos se define como el ángulo
, La ángulo diedro entre ellos se define como el ángulo  entre sus direcciones normales:
entre sus direcciones normales:
Planos en diversas áreas de las matemáticas
Además de su familiarizado geométrica estructura, con isomorfismos que son isometrías con respecto al producto interno habitual, el plano se pueden ver en varios otros niveles de abstracción. Cada nivel de abstracción corresponde a una específica categoría.
En un extremo, todo geométrica y conceptos métricas pueden ser bajado a dejar el topológica avión, lo que puede ser pensado como una idealizada homotópicamente lámina de goma trivial infinita, que conserva una noción de proximidad, pero no tiene distancias. El plano topológico tiene un concepto de una trayectoria lineal, pero el concepto de una línea recta. El avión topológico, o su equivalente el disco abierto, es el barrio topológica básico utilizado para construir superficies (o 2-variedades) clasificados en la de pocas dimensiones topología. Isomorfismos del plano topológico son todos continuo biyecciones. El avión topológico es el contexto natural para la rama de la teoría de grafos que se ocupa de grafos planos, y los resultados como el Teorema de los cuatro colores .
El plano también puede ser visto como una espacio afín, cuya isomorfismos son combinaciones de traducciones y mapas lineales no singulares. Desde este punto de vista no hay distancias, pero colinealidad y proporciones de distancias en cualquier línea se conservan.
Geometría diferencial ve un avión como un verdadero 2-dimensional colector , un plano topológica que está provisto de una estructura diferencial. De nuevo en este caso, no hay noción de distancia, pero ahora hay un concepto de suavidad de mapas, por ejemplo, una diferenciable o camino liso (dependiendo del tipo de estructura diferencial aplicada). Los isomorfismos en este caso son biyecciones con el grado elegido de diferenciabilidad.
En la dirección opuesta de la abstracción, podemos aplicar una estructura de campo compatible con el plano geométrico, dando lugar al plano complejo y el área principal de análisis complejo. El campo complejo tiene sólo dos isomorfismos que salen de la recta real fija, la identidad y conjugación.
De la misma manera que en el caso real, el plano también puede ser visto como el más simple, de una sola dimensión (a través de los números complejos) múltiple compleja, a veces llamada la línea compleja. Sin embargo, este punto de vista contrasta con el caso del avión como un colector real de 2-dimensional. Los isomorfismos son todos biyecciones de conformación del plano complejo, pero las únicas posibilidades son mapas que corresponden a la composición de una multiplicación por un número complejo y de una traducción.
Además, la geometría euclidiana (que tiene cero curvatura en todas partes) no es la única geometría que el avión puede tener. El plano se puede dar una geometría esférica mediante el uso de la proyección estereográfica. Esto puede ser pensado como la colocación de una esfera sobre el plano (al igual que una pelota en el suelo), la eliminación del punto superior, y la proyección de la esfera sobre el plano de este punto). Esta es una de las proyecciones que pueden utilizarse en la fabricación de un mapa plano de una parte de la superficie de la Tierra. La geometría resultante tiene curvatura positiva constante.
Alternativamente, el avión se puede también dar una métrica que le da curvatura negativa constante dando la plano hiperbólico. Esta última posibilidad se encuentra una aplicación de la teoría de la relatividad especial en el caso simplificado, donde hay dos dimensiones espaciales y una dimensión temporal. (El plano hiperbólico es una timelike hipersuperficie en tres dimensiones El espacio de Minkowski.)