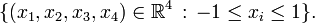Tesseract

Tesseract (8 celdas) 4-cube
Diagrama de Schlegel
Tipo	Polychoron Regular
Familia	hipercubo
Las células	8 ( 4.4.4 )
Caras	24 {4}
Bordes	32
Vértices	16
Figura de la cima	( 3.3.3 )
Símbolos Schläfli	{4,3,3} {4,3} {x} {4} x {4} {4} x {} {} x {} X {} x {} {} x
Diagramas Coxeter-Dynkin
Grupo de simetría	B 4, [3,3,4]
Dual	16 células
Propiedades	convexo

En geometría , el Tesseract, también llamado de 8 celdas o octachoron, es la analógica de cuatro dimensiones del cubo , que es a su vez el tres análogo tridimensional de la plaza . El tesseract es el cubo como el cubo es a la plaza ; o, más formalmente, el tesseract puede ser descrito como una convexa 4-politopo regular de cuya frontera se compone de ocho cúbica las células.

Una generalización del cubo de dimensiones mayores que tres se llama un " hipercubo "," n-cubo "o" polytope medida ". El tesseract es el hipercubo de cuatro dimensiones o 4-cubo.

Rotación de sombra de un hipercubo que gira sobre un eje único

De acuerdo con la Diccionario Inglés de Oxford, la palabra Tesseract fue acuñado y utilizado por primera vez en 1888 por Charles Howard Hinton en su libro Una nueva era de pensamiento, del griego "τέσσερεις ακτίνες" ("cuatro rayos"), en referencia a las cuatro líneas de cada vértice a otros vértices. Algunas personas han llamado a la misma figura una "tetracube", y también simplemente un "hipercubo" (aunque un hipercubo pueden ser de cualquier dimensión).

Geometría

El tesseract se puede construir en un número de maneras diferentes. Como un politopo regular de construido por tres cubos dobladas juntas alrededor de cada borde, tiene Schläfli símbolo {4,3,3}. Construido como un 4D Hyperprism hecho de dos cubos paralelos, que puede ser nombrado como un símbolo compuesto Schläfli {4,3} x {}. Como un duoprism, una Producto cartesiano de dos plazas , puede ser nombrado por un símbolo de Schläfli {4} compuesto x {4}.

Dado que cada vértice de un tesseract es adyacente a cuatro bordes, la figura de la cima del tesseract es un habitual tetraedro . La dual polytope del tesseract se llama hexadecachoron o 16 células, con Schläfli símbolo {3,3,4}.

El tesseract estándar en euclidiana 4-espacio se da como la envolvente convexa de los puntos (± 1, ± 1, ± 1, ± 1). Es decir, que consta de los puntos:

Un tesseract está limitada por ocho hiperplanos (x _i = ± 1). Cada par de hiperplanos no paralelas se cruza para formar 24 caras cuadradas en un tesseract. Tres cubos y tres plazas se cruzan en cada orilla. Hay cuatro cubos, seis cuadrados, y cuatro bordes reunidos en cada vértice. En definitiva, se trata de 8 cubos, 24 plazas, 32 aristas y 16 vértices.

Las proyecciones para 2 dimensiones

La construcción de un hipercubo se puede imaginar la siguiente manera:

• 1-dimensional: Dos puntos A y B se pueden conectar a una línea, dando una nueva línea AB.
• 2-dimensional: Dos líneas paralelas AB y CD se pueden conectar para convertirse en un cuadrado, con las esquinas marcadas como ABCD.
• 3-dimensional: Dos cuadrados paralelos ABCD y EFGH se pueden conectar para convertirse en un cubo, con las esquinas marcadas como ABCDEFGH.
• 4-dimensional: Dos cubos paralelas ABCDEFGH y IJKLMNOP se puede conectar a convertirse en un hipercubo, con las esquinas marcadas como ABCDEFGHIJKLMNOP.

Esta estructura no se imagina fácilmente pero es posible proyectar tesseracts en espacios de tres o de dos dimensiones. Además, las proyecciones sobre el plano 2D se vuelven más instructivo por la reordenación de las posiciones de los vértices proyectados. De esta manera, se pueden obtener imágenes que ya no reflejan las relaciones espaciales dentro de la tesseract, pero que ilustran la estructura de conexión de los vértices, como en los siguientes ejemplos:

Un tesseract está, en principio, obtiene combinando dos cubos. El esquema es similar a la construcción de un cubo de dos cuadrados: yuxtaponer dos copias del cubo dimensional inferior y conectar los vértices correspondientes. Cada borde de un tesseract es de la misma longitud. Una multitud de cubos que están muy bien interconectados. Los vértices del tesseract con respecto a la distancia a lo largo de los bordes, con respecto al punto inferior. Este punto de vista es de interés cuando se utiliza tesseracts como la base para una topología de la red para enlazar múltiples procesadores en computación paralela: la distancia entre dos nodos es como máximo de 4 y hay muchos caminos diferentes para permitir el equilibrio de peso.

Tesseracts son también grafos bipartitos, al igual que un camino, cuadrado, cubo y el árbol son.

Las proyecciones para 3 dimensiones

El dodecaedro rómbico forma el casco de la proyección-vértice primero de un tesseract a 3 dimensiones

Sobres de Proyección de la Tesseract. (Cada célula se dibuja con rostros de color diferentes, las células son invertidos no dispuesto)

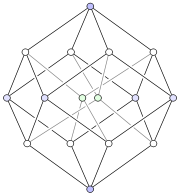
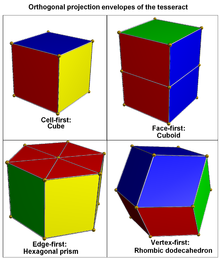
El paralelo de células primero proyección de la tesseract en el espacio 3-dimensional tiene una cúbica sobre. Las células más cercanos y más lejanos se proyectan en el cubo, y los 6 restantes células se proyectan en las 6 caras cuadradas del cubo.

La proyección paralela cara primero del tesseract en el espacio de 3 dimensiones tiene un sobre cúbico. Dos pares de células proyectan para las mitades superior e inferior de este sobre, y los 4 restantes células proyectan a las caras laterales.

La proyección paralela de borde de la primera tesseract en el espacio 3-dimensional tiene un sobre en la forma de un prisma hexagonal. Seis células proyectan en prismas rómbicos, que se colocan en el prisma hexagonal de manera análoga a como las caras del proyecto de cubo 3D en 6 rombos en un sobre hexagonal menores de proyección-vértice primero. Las dos células restantes proyectan sobre las bases del prisma.

La proyección paralela vértice de la primera tesseract en el espacio 3-dimensional tiene una dotación dodecaédrica romboidal. Hay exactamente dos maneras de descomponer un dodecaedro rómbico en 4 congruentes paralelepípedos, dando un total de 8 posibles paralelepípedos. Las imágenes de las células del tesseract bajo esta proyección son precisamente estos 8 paralelepípedos. Esta proyección es también el uno con el volumen máximo.

Despliegue de la Tesseract

El tesseract puede ser desplegada en ocho cubos, al igual que el cubo puede ser desplegada en seis cuadrados. Un despliegue de un politopo es llamado neta. Hay 261 redes distintas de la Tesseract. Los desdoblamientos de la Tesseract se pueden contar por la cartografía de las redes a los árboles apareados (a árbol junto con una juego perfecto en su complemento).

Tesseracts en la cultura popular

Libros / impresión

• La novela de Madeline L'Engle A Wrinkle in Time utiliza tesseracts como una manera para que Meg Murry y sus compañeros para viajar a otros planetas y dimensiones, sin embargo la descripción es más compatible con un agujero de gusano.
• Carl Sagan describe el Tesseract en gran detalle el uso de los términos del laico en Cosmos, el episodio 10.
• En La novela de Edwin A. Abbott Flatland, 1884, un hipercubo es imaginada por el narrador.
• Robert A. Heinlein mencionó hipercubos en al menos tres de sus historias de ciencia ficción. En "-Y Construyó una Crooked House-" (1940), describió una casa construida como una red (es decir, un desarrollo de las células en el espacio tridimensional) de un tesseract. Se derrumbó, convirtiéndose en un verdadero tesseract 4 dimensiones. 1963 la novela de Heinlein Camino a la gloria incluido el foldbox, una caja de embalaje hiperdimensional que era más grande por dentro que por fuera.
• Hipercubos y todo tipo de espacios y estructuras multidimensionales estrella ocupa un lugar destacado en muchos libros de Rudy Rucker.
• Un hipercubo se utiliza como la principal deus ex machina de El libro de Robert J. Sawyer Factoring Humanidad, incluso a aparecer en la portada de América del Norte.
• La novela de Piers Anthony Cubo ruta también cuenta con un tesseract.
• El segundo libro de Alex Garland se llama "Tesseract: una novela".
• La DC Comics cruce DC One Million mostró un futuro de la Tierra en el que las ciudades ocupadas áreas extradimensional llamado tesseracts, dejando la superficie del planeta virgen. Una tecnología similar se utilizó para Superman actual 's Fortaleza de la Soledad, y fue utilizado como espacio de almacenamiento en la sede de la encarnación original (pre- Hora cero) de la Legión de Superhéroes.
• Ciencia ficción Fantástico de Ian Irvine 'Tetrarca' libro dos de la 'El Pozo de Ecos Quartet'.
• David Lubar de 'Sleeping Freshmen Nunca Lie'. Tesseract que significa "espiral hacia otra dimensión."
• Cuento clásico de Lewis Padgett, ' Mimsy Were características borogoves los 'dos niños que construyen un tesseract utilizando la información del futuro. Ellos finalmente desaparecen en otra dimensión.
• Umberto Eco hace referencia en tesseracts El péndulo de Foucault

Artes visuales

• La pintura Crucifixión (Corpus Hypercubus), por Salvador Dalí, de 1954, representa el crucificado Jesús en la red de un hipercubo. Se ofrece en el Museo Metropolitano de Arte de Nueva York, EE.UU. .

Televisión y cine

• La programa de televisión Andrómeda hace uso de generadores tesseract como dispositivo del diagrama. Estos están destinados principalmente para manipular el espacio (también conocido como desplazamiento de fase), pero a menudo causar problemas con el tiempo también.
• Un personaje en el programa de televisión Numb3rs muestra un modelo de un tesseract en el Rampage episodio de la segunda temporada, durante una discusión de la utilización de una perspectiva de 4-dimensional para analizar un evento.
• El programa de TV El Colegio del Agujero Negro tiene un episodio en el campus de la escuela se transforma en un hipercubo auto-plegado.
• La película Cube 2: Hypercube se centra en ocho extraños atrapados dentro de una red de cubos conectados o quizás algún tipo de tesseract que desplaza en la dirección de las 8 extraños movimientos en cualquier dirección, haciendo un continuum aparentemente interminable de cubos singulares.
• La película The Last Mimzy menciona tesseracts en una lista de otras formas geométricas, cuando los niños están soñando con el puente a través del universo, al igual que el cuento en el que se basa, ' Mimsy Were las Borogoves "(mencionados anteriormente). Esto también puede ser en homenaje a A Wrinkle in Time .

Negocios

• Tesseract Libros fue un prominente editor de libros de ciencia ficción canadienses. La empresa es ahora una huella de Hades Publishing Inc.

Video Juegos

• Starflight incluyó un tesseract como un artefacto que podría encontrarse al explorar las superficies planetarias.

Juegos

• Un tesseract forma la base de la fantasía Advanced Dungeons & Dragons módulo La cabaña de Baba Yaga, que apareció en una edición temprana de la revista Dragón, con el Tesseract existente como el interior de la titular Hut.