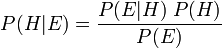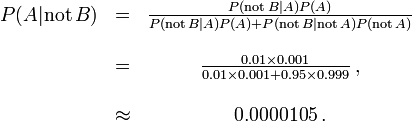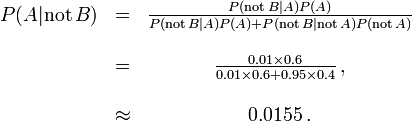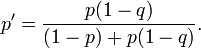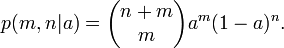Inférence bayésienne

À propos de ce écoles sélection Wikipedia

Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

Inférence bayésienne est inférence statistique dans lequel des preuves ou des observations sont utilisés pour mettre à jour ou nouvellement déduire la probabilité qu'une hypothèse peut être vrai. Le nom "bayésien" vient de l'utilisation fréquente de Le théorème de Bayes dans le processus d'inférence. Le théorème de Bayes a été dérivé du travail du révérend Thomas Bayes.

Preuves et changer les croyances

L'inférence bayésienne utilise les aspects de la méthode scientifique, qui implique la collecte preuve qui est censé être compatible ou incompatible avec une donnée hypothèse. Comme preuve se accumule, le degré de croyance en une hypothèse doit changer. Avec suffisamment de preuves, il devrait devenir très élevé ou très faible. Ainsi, les partisans de l'inférence bayésienne disent qu'il peut être utilisé pour discriminer entre les hypothèses contradictoires: hypothèses à très haute soutien devraient être acceptées comme vraies et ceux qui ont très peu de soutien devraient être rejetés comme faux. Cependant, les détracteurs disent que cette méthode d'inférence peut être biaisée en raison de croyances initiales que l'on doit tenir avant que la preuve ne est jamais recueillies.

Inférence bayésienne utilise une estimation numérique du degré de croyance en une hypothèse avant que la preuve a été observé et calcule une estimation chiffrée du degré de croyance dans l'hypothèse après que la preuve a été observé. Inférence bayésienne repose généralement sur degrés de croyance, ou probabilités subjectives, dans le processus d'induction et ne prétend pas nécessairement de fournir une méthode objective de l'induction. Néanmoins, certains statisticiens bayésiens croire probabilités peuvent avoir une valeur objective et donc inférence bayésienne peut fournir une méthode objective de l'induction. Voir méthode scientifique.

Le théorème de Bayes ajuste probabilités données nouvelles preuves de la façon suivante:

$P (H | E) = \ frac {P (E | H) \; P (H)} {P (E)}$

où

$H$ représente une hypothèse spécifique, qui peuvent ou peuvent ne pas être quelque hypothèse nulle.
$P (H)$ est appelé le de probabilité a priori $H$ qui a été déduit avant de nouvelles preuves, $E$ , Est devenu disponible.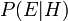
$P (E | H)$ est appelé le probabilité conditionnelle de voir la preuve $E$ si l'hypothèse $H$ passe pour être vrai. Il est aussi appelé un fonction de vraisemblance lorsque l'on considère comme une fonction de $H$ pour fixe $E$ .
$P (E)$ est appelé le de probabilité marginale $E$ : La probabilité a priori d'être témoin de la nouvelle preuve $E$ sous toutes les hypothèses possibles. Il peut être calculé comme la somme du produit de toutes les probabilités de ne importe quel ensemble complet d'hypothèses mutuellement exclusives et probabilités conditionnelles correspondantes: $P (E) = \ sum P (E | h_i) P (h_i)$ .
$P (H | E)$ est appelé le probabilité postérieure de $H$ donné $E$ .

Le facteur $P (E | M) / P (E)$ représente l'incidence que la preuve a sur la croyance dans l'hypothèse. Se il est probable que la preuve $E$ serait observée lorsque l'hypothèse à l'étude est vrai, mais peu probable que $E$ aurait été le résultat de l'observation, ce facteur sera grand. La multiplication de la probabilité a priori de l'hypothèse par ce facteur se traduirait par une plus grande probabilité a posteriori de l'hypothèse étant donné la preuve. Inversement, se il est peu probable que la preuve $E$ serait observée si l'hypothèse à l'étude est vrai, mais a priori probable que $E$ serait observée, le facteur réduirait la probabilité a posteriori pour $H$ . Sous l'inférence bayésienne, le théorème de Bayes mesure donc combien de nouveaux éléments de preuve devrait modifier une croyance en une hypothèse.

Statisticiens bayésiens soutiennent que même lorsque les gens sont très différentes probabilités subjectives antérieures, de nouvelles preuves à partir d'observations répétées aura tendance à apporter leurs postérieurs probabilités subjectives rapprocher. Cependant, d'autres soutiennent que lorsque les gens tiennent largement différente subjective avant leurs probabilités postérieures probabilités subjectives ne peuvent jamais converger même avec la collecte répétée de preuves. Ces critiques font valoir que les visions du monde qui sont complètement différentes d'abord peuvent rester complètement différente au fil du temps malgré une forte accumulation de preuves.

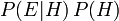Multipliant la probabilité a priori $P (H)$ par le facteur $P (E | M) / P (E)$ ne sera jamais donné une probabilité qui est supérieure à 1, étant donné que $P (E)$ est au moins aussi grande que $P (E \ cap H)$ (Où $\ Cap$ désigne "et"), ce qui équivaut à $P (E | H) \, P (H)$ (Voir probabilité conjointe).

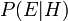La probabilité de $E$ donné $H$ , $P (E | H)$ , Peut être représenté comme une fonction de son second argument avec son premier argument maintenu fixe. Une telle fonction est appelée fonction de vraisemblance; ce est une fonction de $H$ seul, avec $E$ traité comme un paramètre. Un rapport de deux fonctions de vraisemblance est appelé un rapport de vraisemblance, 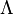$\ Lambda$ . Par exemple,

$\ Lambda_E = \ frac {L (H | E)} {L (\ mathrm {pas} \, H | E)} = \ frac {P (E | H)} {P (E | \ mathrm {pas} \ , H)}$ ,

où la dépendance de $\ Lambda_E$ sur $H$ est supprimée pour plus de simplicité (comme $E$ aurait pu être, sauf que nous aurons besoin d'utiliser ce paramètre ci-dessous).

Depuis $H$ et non- $H$ sont mutuellement exclusives et couvrent toutes les possibilités, la somme précédemment donnée pour la probabilité marginale réduit à $P (E) = P (E | H) \, P (H) + P (E | \ mathrm {pas} \, H) \, P (\ mathrm {pas} \, H)$ . Par conséquent, nous pouvons réécrire le théorème de Bayes que

$P (H | E) = \ frac {P (E | H) \, P (H)} {P (E | H) \, P (H) + P (E | \ mathrm {pas} \, H) \, P (\ mathrm {pas} \, H)} = \ frac {\ Lambda_E P (H)} {\ Lambda_E P (H) + P (\ mathrm {pas} \, H)}$ .

Nous pourrions alors exploiter l'identité $P (\ mathrm {pas} \, H) = 1 - P (H)$ à exposer $P (H | E)$ en fonction de la juste $P (H)$ (Et $\ Lambda_E$ , Qui est calculé directement à partir de la preuve).

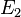Avec deux pièces indépendantes de preuve $E_1$ et $E_2$ , Inférence bayésienne peut être appliquée de manière itérative. Nous pourrions utiliser le premier élément de preuve pour calculer une probabilité postérieure initiale, puis utiliser cette probabilité a posteriori comme une nouvelle probabilité a priori pour calculer une seconde probabilité a posteriori donnée le deuxième élément de preuve. Le théorème de Bayes donne appliqué de manière itérative

$P (H | E_1 \ cap E_2) = \ frac {P (E_2 | H) \; P (E_1 | H) \, P (H)} {P (E_2) \; P (E_1)}$

Utilisation de rapports de vraisemblance, nous constatons que

$P (H | E_1 \ cap E_2) = \ frac {\ Lambda_1 \ Lambda_2 P (H)} {[\ Lambda_1 P (H) + P (\ mathrm {pas} \, H)] \; [\ Lambda_2 P ( H) + P (\ mathrm {pas} \, H)]}$ ,

Cette itération de l'inférence bayésienne pourrait être étendue avec des morceaux plus indépendantes de preuve.

Inférence bayésienne est utilisée pour calculer les probabilités pour la prise de décision en situation d'incertitude. En plus des probabilités, une fonction de perte doit être évalué pour tenir compte de l'impact relatif des alternatives.

Des exemples simples de l'inférence bayésienne

À partir de laquelle bol est le cookie?

Pour illustrer, supposons qu'il y ait deux coupes pleines de biscuits. Bowl n ° 1 a 10 pépites de chocolat et 30 biscuits secs, tout en bol n ° 2 a 20 de chaque. Notre ami Fred prend un bol au hasard, puis prend un cookie au hasard. On peut supposer qu'il n'y a pas de raison de croire Fred traite une cuvette différemment d'un autre, même pour les cookies. Le cookie se avère être un simple. Comment est-il probable que Fred a pris hors de bol n ° 1?

Intuitivement, il semble clair que la réponse devrait être plus de la moitié, car il ya des cookies plus simples dans un bol # 1. La réponse précise est donnée par le théorème de Bayes. Laisser $H_1$ correspondre à bol n ° 1, et $H_2$ bol # 2. Elle est donnée que les bols sont identiques du point de vue de Fred, ainsi $P (H_1) = P (H_2)$ , Et les deux doivent être égales à 1, de sorte que les deux sont égaux à 0,5. L'événement $E$ est l'observation d'un cookie plaine. A partir des contenus des cuvettes, on sait que $P (E | H_1) = 30/40 = 0,75$ et $P (E | H_2) = 20/40 = 0,5$ . La formule de Bayes donne alors

$\ Begin {matrix} P (H_1 | E) & = & \ frac {P (E | H_1) \, P (H_1)} {P (E | H_1) \, P (H_1) \; + \; P ( E | H_2) \, P (H_2)} \\ \\ \ & = & \ frac {0,75 \ fois 0,5} {\ 0,75 fois 0,5 + 0,5 \ times 0,5} \\ \\ \ & = & 0,6 \ end { matrix}$

Avant nous avons observé le cookie, la probabilité nous avons attribué pour Fred ayant choisi bol n ° 1 était la probabilité a priori, 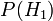$P (H_1)$ , Qui était de 0,5. Après avoir observé le cookie, nous devons réviser la probabilité de $P (H_1 | E)$ , Qui est de 0,6.

Les faux positifs dans un test médical

Les faux positifs se produisent lorsque un test faussement ou mal fait état d'un résultat positif. Par exemple, un test médical pour une maladie peut renvoyer un résultat positif indiquant que le patient a une maladie, même si le patient n'a pas la maladie. Nous pouvons utiliser le théorème de Bayes pour déterminer la probabilité qu'un résultat positif est en fait un faux positif. Nous constatons que si une maladie est rare, alors la majorité des résultats positifs peut être faux positifs, même si le test est exacte.

Supposons qu'un test pour une maladie génère les résultats suivants:

Si un patient a testé la maladie, le test renvoie un résultat positif 99% du temps, ou avec une probabilité de 0,99
Si un patient testé n'a pas la maladie, le test renvoie un résultat positif de 5% du temps, ou avec une probabilité de 0,05.

Naïvement, on pourrait penser que seulement 5% des résultats positifs sont faux, mais ce est tout à fait tort, comme nous le verrons.

Supposons que seulement 0,1% de la population a cette maladie, de sorte que le patient sélectionné au hasard a une probabilité a priori d'avoir la maladie 0,001.

Nous pouvons utiliser le théorème de Bayes pour calculer la probabilité qu'un résultat positif est un faux positif.

Soit A représente la condition dans laquelle le patient présente la maladie, et B représentent la déposition d'un résultat de test positif. Ensuite, la probabilité que le patient a effectivement la maladie étant donné le résultat de test positif est

$\ Begin {matrix} P (A | B) & = & \ frac {P (B | A) P (A)} {P (B | A) P (A) + P (B | \ mathrm {pas} \ , A) P (\ mathrm {pas} \, A)} \\ \\ & = & \ frac {0,99 \ fois 0,001} {\ 0,99 fois 0,001 + 0,05 \ times 0,999} ~ \\ \\ & \ approx & 0 0,019. \ end {matrix}$

et donc la probabilité qu'un résultat positif est un faux positif est d'environ 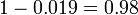$1 à 0,019 = 0,98$ , Ou 98%.

Malgré la haute précision apparente de l'essai, l'incidence de la maladie est si faible que la grande majorité des patients séropositifs ne ont pas la maladie. Néanmoins, la fraction des patients séropositifs qui ne ont la maladie (0,019) est 19 fois la fraction de personnes qui ne ont pas encore passé le test qui ont la maladie (0,001). Ainsi, le test ne est pas inutile, et re-tests peut améliorer la fiabilité du résultat.

Afin de réduire le problème des faux positifs, un test doit être très précis dans des rapports de résultat négatif lorsque le patient n'a pas la maladie. Si le test a rapporté un résultat négatif chez les patients sans la maladie avec une probabilité de 0,999, alors

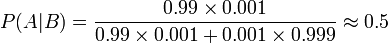$P (A | B) = \ frac {0,99 \ fois 0,001} {\ 0,99 fois 0,001 + 0,001 0,999} \ times \ environ 0,5$ ,

de sorte que 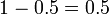$1 à 0,5 = 0,5$ Il est maintenant la probabilité d'un faux positif.

D'autre part, faux négatifs se produisent lorsque un test faussement ou mal fait état d'un résultat négatif. Par exemple, un test médical pour une maladie peut renvoyer un résultat négatif indiquant que le patient n'a pas une maladie, même si le patient a réellement la maladie. Nous pouvons également utiliser le théorème de Bayes pour calculer la probabilité d'un faux négatif. Dans le premier exemple ci-dessus,

$\ Begin {matrix} P (A | \ mathrm {pas} \, B) & = & \ frac {P (\ mathrm {pas} \, B | A) P (A)} {P (\ mathrm {} pas \, B | A) P (A) + P (\ mathrm {pas} \, B | \ mathrm {pas} \, A) P (\ mathrm {pas} \, A)} \\ \\ & = & \ frac {0,01 \ fois 0,001} {\ 0,01 fois 0,001 + 0,95 \ times 0,999} \, \\ ~ \\ & \ & environ 0,0000105 \,. \ end {matrix}$

La probabilité qu'un résultat négatif est un faux négatif est d'environ 0,00105% ou 0.0000105. Quand une maladie est rare, les faux négatifs ne seront pas un problème majeur avec le test.

Mais si 60% de la population avait la maladie, alors la probabilité d'un faux négatif serait plus grande. Avec le test ci-dessus, la probabilité d'un faux négatif serait

$\ Begin {matrix} P (A | \ mathrm {pas} \, B) & = & \ frac {P (\ mathrm {pas} \, B | A) P (A)} {P (\ mathrm {} pas \, B | A) P (A) + P (\ mathrm {pas} \, B | \ mathrm {pas} \, A) P (\ mathrm {pas} \, A)} \\ \\ & = & \ frac {0,01 \ fois 0,6} {\ 0,01 fois 0,6 + 0,95 \ times 0,4} \, \\ ~ \\ & \ & environ 0,0155 \,. \ end {matrix}$

La probabilité qu'un résultat négatif est un faux négatif se élève à 0,0155 ou 1,55%.

Dans la salle d'audience

Inférence bayésienne peut être utilisé dans un cadre judiciaire par un des jurés de se accumuler de manière cohérente les preuves pour et contre la culpabilité de l'accusé, et de voir si, dans sa totalité, il satisfait leur seuil personnelle pour «au-delà de tout doute raisonnable».

Laisser 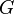$Sol$ désigner le cas où l'accusé est coupable.

Laisser $E$ désigner le cas où l'ADN de l'accusé correspond à l'ADN trouvé sur les lieux du crime.

Laisser 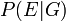$P (E | G)$ désigner la probabilité de l'événement voir $E$ si le défendeur est effectivement coupable. (Habituellement, cela serait considéré comme unité.)

Laisser 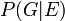$P (G | E)$ désigner la probabilité que l'accusé est coupable en supposant que le match de l'ADN (événement $E$ ).

Laisser $P (G)$ désigner estimation personnelle du juré de la probabilité que l'accusé est coupable, sur la base de la preuve autre que le match d'ADN. Ce pourrait être basé sur ses réponses au titre du questionnement, ou la preuve présentée précédemment.

Inférence bayésienne nous dit que si nous pouvons attribuer une probabilité p (G) à la culpabilité de l'accusé avant de prendre la preuve d'ADN en compte, alors nous pouvons réviser cette probabilité à la probabilité conditionnelle 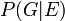$P (G | E)$ Car

$P (G | E) = \ frac {P (G) P (E | G)} {P (E)}$

Supposons, sur la base d'autres éléments de preuve, un juré décide qu'il ya une chance de 30% que l'accusé est coupable. Supposons également que le témoignage judiciaire était que la probabilité qu'une personne choisie au hasard aurait ADN qui correspondait à celui à la scène de crime est de 1 sur un million, ou 10 ^-6.

L'événement E peut se produire de deux façons. Soit l'accusé est coupable (avec une probabilité avant 0,3) et donc son ADN est présent avec une probabilité 1, ou qu'il est innocent (avec une probabilité de 0,7 avant) et il est assez malchanceux pour être l'un des 1 à un million le rapprochement des personnes.

Ainsi le juré pourrait réviser son opinion de manière cohérente afin de tenir compte de la la preuve d'ADN comme suit:

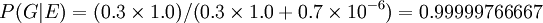$P (G | E) = (0,3 \ 1,0 fois) /(0.3 \ times 1,0 + 0,7 \ times 10 ^ {- 6}) = ,99999766667$ .

L'avantage de l'adoption d'une approche bayésienne est qu'elle donne le juré un mécanisme formel pour combiner la preuve présentée. L'approche peut être appliquée successivement à tous les éléments de preuve présentés au tribunal, avec la partie postérieure d'une étape de devenir l'avant pour la prochaine.

Le juré aurait encore d'avoir une estimation préalable de la probabilité de la culpabilité avant le premier élément de preuve est considéré. Il a été suggéré que cela pourrait être raisonnablement la probabilité d'une personne aléatoire tiré de la population admissible de culpabilité. Ainsi, pour un crime connu pour avoir été commis par un adulte de sexe masculin vivant dans une ville contenant 50 000 hommes adultes, la probabilité a priori initiale appropriée pourrait être 1/50000.

Ajout jusqu'à preuve.

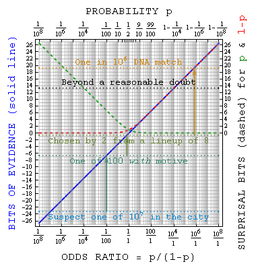
Pour le but d'expliquer le théorème de Bayes aux jurés, il sera généralement approprié de donner dans la forme de Pari plutôt que des probabilités, que ceux-ci sont plus largement compris. Dans les Etats théorème de Bayes que ce formulaire

cotes postérieures = antérieures cotes x Facteur de Bayes

Dans l'exemple ci-dessus, le juré qui a une probabilité a priori de 0,3 pour le défendeur coupable serait désormais exprimer que sous la forme de cote de 3: 7 en faveur de l'accusé coupable, le facteur de Bayes est d'un million, et la résultante cotes postérieures sont 3 millions à 7 ou à propos de 429 000 à un en faveur de la culpabilité.

Un approche logarithmique qui remplace multiplication par addition et réduit la plage des numéros concernés pourrait être plus facile pour un jury de gérer. Cette approche, développée par Alan Turing pendant la Seconde Guerre mondiale et plus tard promu par IJ Bien et ET Jaynes entre autres, revient à l'utilisation de entropie de l'information.

Au Royaume-Uni, le théorème de Bayes a été expliqué au jury sous la forme de cotes par un statisticien témoin expert dans le cas du viol Regina contre Denis John Adams. Une condamnation a été fixée mais le litige en appel, car aucun moyen d'accumulation de preuves avaient été fournis pour les jurés qui ne veulent pas utiliser le théorème de Bayes. La Cour d'appel a confirmé la condamnation, mais a également donné leur avis que «Pour introduire le théorème de Bayes, ou toute autre méthode similaire, dans un procès criminel plonge le Jury dans les royaumes inappropriés et inutiles de la théorie et de la complexité, les déviant de leur tâche propre. " Aucune autre appel a été accueilli et la question de l'évaluation bayésienne des données d'ADN médico-légale reste controversée.

Gardner-Medwin fait valoir que le critère sur lequel devrait se fonder un verdict dans un procès criminel ne est pas la probabilité de culpabilité, mais plutôt la probabilité de la preuve, étant donné que le défendeur est innocent (semblable à un fréquentiste p-valeur). Il fait valoir que si la probabilité postérieure de culpabilité doit être calculée par le théorème de Bayes, la probabilité a priori de culpabilité doit être connue. Cela dépendra de l'incidence de la criminalité, qui est un élément de preuve inhabituelle à considérer dans un procès criminel. Considérons les trois propositions suivantes:

A: les faits et les témoignages connus qui auraient pu surgir si l'accusé est coupable,

B: Les faits et témoignages connus auraient pu survenir si le défendeur est innocent,

C: L'accusé est coupable.

Gardner-Medwin fait valoir que le jury doit croire à la fois A et non-B pour condamner. A et non-B implique la vérité de C, mais l'inverse ne est pas vrai. Il est possible que B et C sont à la fois vrai, mais dans ce cas il fait valoir que le jury doit acquitter, même se ils savent qu'ils seront laissent certaines personnes coupables en liberté. Voir également Le paradoxe de Lindley.

Autres affaires judiciaires dans lesquelles des arguments probabilistes joué un certain rôle étaient les Howland sera faux procès, le Cas Sally Clark, et de la Lucia de Berk cas.

la théorie de la Recherche

En mai 1968, le sous-marin nucléaire d'US Scorpion (SSN-589) ne est pas arrivé comme prévu à son port d'attache Norfolk, en Virginie. L'US Navy a été convaincu que le navire avait été perdu au large de la côte Est, mais une recherche approfondie échoué à découvrir l'épave. Expert en eau profonde de l'US Navy, John Craven USN, a estimé qu'il était ailleurs et il a organisé une recherche sud-ouest de la Açores basée sur une triangulation approximative controversée par des hydrophones. Il a été alloué un seul navire, le Mizar, et il a pris les conseils d'un cabinet de mathématiciens de consultants afin de maximiser ses ressources. Une méthodologie de recherche bayésienne a été adopté. Commandants de sous-marins expérimentés ont été interrogés pour construire des hypothèses sur ce qui pourrait avoir causé la perte du Scorpion.

La zone de la mer a été divisée en cases de la grille et une probabilité attribuée à chaque carré, sous chacune des hypothèses, de donner un certain nombre de grilles de probabilité, une pour chaque hypothèse. Ils ont ensuite été ajoutés ensemble pour produire une grille globale de probabilité. La probabilité attaché à chaque place était alors la probabilité que l'épave était dans ce carré. Une seconde grille a été construit avec des probabilités qui représentent la probabilité de trouver avec succès l'épave si cette place devait être recherché et l'épave devait être vraiment là. Ce est une fonction connue de la profondeur de l'eau. Le résultat de la combinaison cette grille avec la grille précédente est une grille qui donne la probabilité de trouver l'épave dans chaque carré de la grille de la mer si elle devait être recherché.

Cette grille de mer était systématiquement recherchée d'une manière qui a commencé avec les régions élevées de probabilité première et travaillé jusque dans les régions de faible probabilité derniers. Chaque fois qu'un carré de la grille a été fouillé et trouvé vide sa probabilité a été réévaluée en utilisant Le théorème de Bayes. Ce ensuite forcé les probabilités de toutes les autres cases de la grille d'être réévalués (vers le haut), aussi par le théorème de Bayes. L'utilisation de cette approche a été un défi majeur pour le calcul du temps, mais il a finalement été couronnée de succès et le Scorpion a été retrouvée à environ 740 km sud-ouest de la Açores en Octobre de cette année. Supposons qu'un carré de la grille a une probabilité p de contenir l'épave et que la probabilité de détecter avec succès l'épave si ce est il ya q. Si la place est fouillé et aucune épave ne est trouvé, alors, par le théorème de Bayes, la probabilité révisée de l'épave étant sur la place est donnée par

$p '= \ frac {p (1-q)} {(1-p) + p (1-q)}.$

Plus exemples mathématiques

Classification naïve bayésienne

Voir naïve classificateur de Bayes.

La distribution a posteriori du paramètre binomiale

Dans cet exemple, nous considérons le calcul de la distribution a posteriori pour le paramètre binomial. Ce est le même problème considéré par Bayes dans la proposition 9 de son essai.

On nous donne m observé succès et échecs n observé dans une expérience binomiale. L'expérience peut être jeter une pièce de monnaie, en tirant une balle dans une urne, ou demander à quelqu'un de leur avis, parmi beaucoup d'autres possibilités. Ce que nous savons sur le paramètre (appelons-le a) est indiqué que la distribution a priori, p (a).

Pour une valeur donnée de a, la probabilité de succès en m m + n est essais

$p (m, n | a) = \ begin {} pmatrix n + m \\ m \ end {} pmatrix un ^ m (1-a) ^ n.$

Étant donné que m et n sont fixes, et a est inconnu, ce est une fonction de la probabilité pour un. De la forme continue de la loi de probabilité total, nous avons

$p (a | m, n) = \ frac {p (m, n | a) \, P (A)} {\ ^ int_0 1 p (m, n | a) \, p (a) \, da} = \ frac {\ begin {} pmatrix n + m \\ m \ end {} pmatrix un ^ m (1-a) ^ n \, p (a)} {\ int_0 ^ 1 \ begin {} pmatrix n + m \\ m \ end {} pmatrix un ^ m (1-a) ^ n \, p (a) \, da}.$

Pour certains choix particulier de la distribution a priori p (a), l'intégrale peut être résolu et la partie arrière prend une forme commode. En particulier, si p (a) est un la distribution bêta avec des paramètres m et n _{0 0,} puis la partie postérieure est également une distribution bêta avec des paramètres m + ₀ m et n + n _0.

Un Conjugué avant est une distribution a priori, tels que la distribution bêta dans l'exemple ci-dessus, qui a la propriété que la partie postérieure est le même type de distribution.

Ce qui est "bayésien" à propos de la Proposition 9 est que Bayes présenté comme une probabilité pour le paramètre a. Ce est, non seulement une probabilités de calcul pour les résultats expérimentaux, mais aussi pour le paramètre qui les régit, et même l'algèbre est utilisé pour faire des inférences de type soit possible. Fait intéressant, Bayes affirme effectivement sa question d'une manière qui pourrait faire l'idée d'attribuer une distribution de probabilité à un paramètre acceptable pour un fréquentiste. Il suppose que une boule de billard est jeté au hasard sur une table de billard, et que les probabilités p et q sont les probabilités que les boules de billard suivantes tomberont dessus ou en dessous de la première balle. En faisant le paramètre binomial un dépend d'un événement aléatoire, il se échappe habilement un bourbier philosophique qui était une question qu'il était probablement même pas au courant.

Applications informatiques

Inférence bayésienne a des applications dans l'intelligence artificielle et systèmes experts. Techniques d'inférence bayésienne ont été un élément fondamental du informatisée techniques de reconnaissance des formes depuis la fin des années 1950. Il ya aussi une connexion sans cesse croissant entre les méthodes bayésienne et axés sur la simulation Monte Carlo techniques puisque les modèles complexes ne peuvent pas être traitées sous forme fermée par une analyse bayésienne, tandis que le structure de modèle graphique inhérente aux modèles statistiques, peut permettre algorithmes de simulation efficaces comme le Échantillonnage de Gibbs et autres Régimes de l'algorithme de Metropolis-Hastings. Récemment inférence bayésienne a gagné en popularité parmi les communauté phylogénétique pour ces raisons; des applications telles que BEAST, MrBayes et P4 permettre à de nombreux paramètres démographiques et évolutifs à estimer simultanément.

Appliqué à classification statistique, inférence bayésienne a été utilisée ces dernières années pour développer des algorithmes pour identifier non sollicité en vrac e-mail du spam. Les applications qui font usage de l'inférence bayésienne pour le filtrage de spam comprennent DSPAM, Bogofilter, SpamAssassin, InBoxer, et Mozilla. classement de Spam est traité plus en détail dans l'article sur le naïve classificateur de Bayes.

Dans certaines applications, la logique floue est une alternative à l'inférence bayésienne. La logique floue et l'inférence bayésienne, cependant, sont mathématiquement et sémantiquement pas compatible: Vous ne pouvez pas, en général, comprendre le degré de vérité dans la logique floue que la probabilité et vice versa.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Bayesian_inference&oldid=202156209 "

Privacy Policy and Contacts (IT)