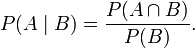Probabilité
Contexte des écoles Wikipédia
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. parrainage SOS enfant est cool!
| série Certitude |
|---|
|
Probabilité la probabilité ou la chance que quelque chose est le cas ou va se passer. La théorie des probabilités est largement utilisé dans des domaines tels que les statistiques , les mathématiques , la science et la philosophie de tirer des conclusions quant à la probabilité d'événements potentiels et les mécanismes sous-jacents des systèmes complexes.
Interprétations
Le mot probabilité n'a pas une définition cohérente directe. En fait, il ya deux grandes catégories d'interprétations de probabilité: Fréquentistes parlent de probabilités que lorsqu'il se agit de bien défini expériences aléatoires. La fréquence relative de l'occurrence du résultat de l'expérience, quand on répète l'expérience, est une mesure de la probabilité de ce phénomène aléatoire. Bayésiens, cependant, attribuer des probabilités à toute déclaration que ce soit, même si aucun processus aléatoire est impliqué, comme un moyen de représenter sa plausibilité subjective.
Histoire
L'étude scientifique de la probabilité est un développement moderne. Le jeu montre qu'il ya eu un intérêt à quantifier les idées de probabilité pour des millénaires, mais des descriptions mathématiques exactes d'utilisation dans ces problèmes ne se pose beaucoup plus tard.
Selon Richard Jeffrey, "Avant le milieu du XVIIe siècle, le terme (de probabilis latine)" probable "signifiait approuvabilité, et a été appliqué dans ce sens, de manière univoque, à l'opinion et à l'action. Une action ou opinion probable était une telle que les gens sensés se engageraient ou de détenir, dans les circonstances. "
Mis à part quelques considérations élémentaires faites par Jérôme Cardan au 16ème siècle, la doctrine des probabilités remonte à la correspondance de Pierre de Fermat et Blaise Pascal (1654). Christiaan Huygens (1657) a donné le traitement scientifique la plus ancienne connue du sujet. Jakob Bernoulli de Ars Conjectandi (posthume, 1713) et Abraham de Moivre de Doctrine de Chances (1718) traite le sujet comme une branche des mathématiques. Voir Ian Hacking est l'émergence de la probabilité pour une histoire du développement précoce de la notion même de probabilité mathématique.
La théorie des erreurs peut être retracée à De Roger Cotes Opera Miscellanea (posthume, 1722), mais un mémoire préparé par Thomas Simpson en 1755 (imprimé 1756) d'abord appliqué la théorie à la discussion des erreurs d'observation. La réimpression (1757) de ce mémoire fixe les axiomes que les erreurs positives et négatives sont également probables, et qu'il ya certaines limites assignables dans lequel toutes les erreurs peuvent être censés tomber; des erreurs continues sont discutés et une courbe de probabilité est donnée.
Pierre-Simon Laplace (1774) fait la première tentative de déduire une règle pour la combinaison des observations des principes de la théorie des probabilités. Il a représenté la loi de probabilité des erreurs par une courbe  ,
, 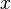 étant une erreur et
étant une erreur et  sa probabilité, et a posé trois propriétés de cette courbe:
sa probabilité, et a posé trois propriétés de cette courbe:
- il est symétrique par rapport à la
 axe des;
axe des; - la
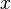 est un axe des asymptote, la probabilité de l'erreur
est un axe des asymptote, la probabilité de l'erreur 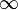 étant égal à 0;
étant égal à 0; - l'espace clos est de 1, il est certain qu'une erreur existe.
Il en déduit une formule pour la moyenne de trois observations. Il a également donné (1781) une formule pour la loi de l'installation d'erreur (un terme en raison de Lagrange, 1774), mais celui qui a conduit à des équations ingérables. Daniel Bernoulli (1778) a introduit le principe du produit maximum les probabilités d'un système d'erreurs simultanées.
La méthode des moindres carrés est due à Adrien-Marie Legendre (1805), qui l'a introduit dans ses Nouvelles Méthodes verser la détermination des Orbites des comètes (Nouvelles méthodes pour déterminer les orbites des comètes). Dans l'ignorance de la contribution de Legendre, un écrivain irlando-américain, Robert Adrain, rédacteur en chef de "The Analyst" (1808), d'abord déduit la loi de l'installation de l'erreur,
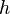 étant une constante fonction de la précision de l'observation, et
étant une constante fonction de la précision de l'observation, et  un facteur d'échelle en sorte que l'aire sous la courbe est égale à 1. Il a donné deux épreuves, la deuxième étant essentiellement la même que John Herschel (1850). Gauss a donné la première preuve qui semble avoir été connu en Europe (le troisième après Adrain de) en 1809. D'autres preuves ont été données par Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), WF Donkin (1844, 1856), et Morgan Crofton (1870). Autres contributeurs étaient Ellis (1844), De Morgan (1864), Glaisher (1872), et Giovanni Schiaparelli (1875). (1856) formule de Peters pour
un facteur d'échelle en sorte que l'aire sous la courbe est égale à 1. Il a donné deux épreuves, la deuxième étant essentiellement la même que John Herschel (1850). Gauss a donné la première preuve qui semble avoir été connu en Europe (le troisième après Adrain de) en 1809. D'autres preuves ont été données par Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), WF Donkin (1844, 1856), et Morgan Crofton (1870). Autres contributeurs étaient Ellis (1844), De Morgan (1864), Glaisher (1872), et Giovanni Schiaparelli (1875). (1856) formule de Peters pour  , L'erreur probable d'une seule observation, est bien connue.
, L'erreur probable d'une seule observation, est bien connue.
Dans les dix-neuvième siècle auteurs sur la théorie générale inclus Laplace , Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, et Karl Pearson. Augustus De Morgan et George Boole a amélioré l'exposé de la théorie.
Sur le côté géométrique (voir géométrie) apportent une contribution essentielle à Les temps étaient éducatifs influente (Miller, Crofton, McColl, Wolstenholme, Watson, et Artemas Martin).
Traitement mathématique
En mathématiques une probabilité d'un cas, A est représenté par un nombre réel dans la gamme de 0 à 1 et écrit comme P (A), P (A) ou Pr (A). Un événement impossible a une probabilité de 0, et un certain événement a une probabilité de 1. Toutefois, les converses sont pas toujours vrai: la probabilité 0 événements ne sont pas toujours impossible, ni une probabilité certaine événements. La distinction assez subtile entre «certaine» et «probabilité 1" est traité plus en détail dans l'article sur " presque sûrement ".
Le complément ou en face d'un événement est l'événement A [non A] (qui est, le cas de pas se produire); sa probabilité est donnée par
. A titre d'exemple, la probabilité de ne pas rouler un six sur un dé à six faces est
=  . Voir Événement complémentaires pour un traitement plus complet.
. Voir Événement complémentaires pour un traitement plus complet.
Si deux événements, A et B sont indépendante alors le probabilité conjointe est
par exemple, si deux pièces sont retournées la chance des deux étant chefs est  .
.
Si deux événements sont mutuellement exclusives alors la probabilité de soit d'origine est
Par exemple, le risque d'un roulement 1 ou 2 sur un dé à six faces est  .
.
Si les événements ne sont pas mutuellement exclusives alors
 .
.
Probabilité conditionnelle est la probabilité d'un événement A, étant donné l'occurrence de quelque autre événement B. Probabilité conditionnelle est écrit P (A | B), et est lu "la probabilité de A, B donnée". Elle est définie par
Si 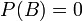 puis
puis 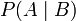 est undefined.
est undefined.
| Événement | Probabilité |
|---|---|
| Un | ![P (A) \ in [0,1] \,](../../images/135/13538.png) |
| Un pas |  |
| A ou B | 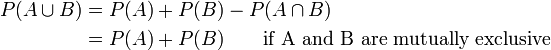 |
| A et B | 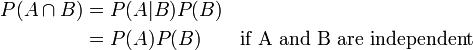 |
| Une donnée B | 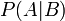 |
Théorie
Comme les autres théories, la théorie des probabilités est une représentation des concepts probabilistes en termes formels qui est, en termes qui peuvent être considérés séparément de leur sens. Ces termes formels sont manipulés par les règles des mathématiques et de la logique, et tous les résultats sont ensuite interprétés ou traduits de nouveau dans le domaine du problème.
Il ya eu au moins deux tentatives réussies pour formaliser probabilité, à savoir la La formulation et l'Kolmogorov Cox formulation. Dans la formulation de Kolmogorov (voir l'espace de probabilité ), ensembles sont interprétées comme des événements et de la probabilité se en tant que mesurer sur une classe d'ensembles. En Théorème, la probabilité de Cox est considéré comme une primitive (ce est pas encore analysé) et l'accent est mis sur la construction d'une affectation cohérente des valeurs de probabilité à des propositions. Dans les deux cas, la lois de probabilité sont les mêmes, sauf pour les détails techniques.
Il existe d'autres procédés pour quantifier l'incertitude, comme le Théorie de Dempster-Shafer et la théorie des possibilités, mais ce sont essentiellement différents et non compatibles avec les lois de la probabilité car ils sont généralement comprises.
Applications
Deux principales applications de la théorie des probabilités dans la vie quotidienne sont en évaluation des risques et dans le commerce sur les marchés des produits de base. Les gouvernements se appliquent généralement à des méthodes probabilistes réglementation environnementale où il est appelé " l'analyse des voies », souvent mesurer le bien-être en utilisant des méthodes qui sont de nature stochastique, et le choix des projets à entreprendre repose sur des analyses statistiques de leur effet probable sur la population dans son ensemble. Il ne est pas exact de dire que les statistiques sont impliqués dans la modélisation elle-même, comme typiquement les évaluations de risques sont un temps et nécessite donc des modèles de probabilité plus fondamentales, par exemple, "la probabilité d'un autre 9/11". Un loi des petits nombres tend à se appliquer à tous ces choix et la perception de l'effet de ces choix, ce qui rend les mesures de probabilité sur une matière politique.
Un bon exemple est l'effet de la probabilité perçue de tout conflit au Moyen-Orient généralisée sur les prix du pétrole - qui ont des effets d'entraînement dans l'économie dans son ensemble. Une évaluation par un commerçant de produits de base que la guerre est plus probable contre moins susceptibles envoie les prix vers le haut ou vers le bas, et les signaux d'autres commerçants de cet avis. En conséquence, les probabilités ne sont pas évalués de manière indépendante ni nécessairement très rationnelle. La théorie de la finance comportementale émergé pour décrire l'effet d'une telle la pensée de groupe sur les prix, sur la politique et sur la paix et les conflits.
On peut raisonnablement dire que la découverte de méthodes rigoureuses pour évaluer et combiner des évaluations de probabilité a eu un effet profond sur la société moderne. En conséquence, il peut être d'une certaine importance à la plupart des citoyens de comprendre comment les cotes et les évaluations de probabilité sont faites, et comment ils contribuent à la réputation et aux décisions, surtout dans une démocratie .
Une autre application importante de la théorie des probabilités dans la vie quotidienne est la fiabilité. De nombreux produits de consommation, tels que les voitures et les appareils électroniques grand public, d'utiliser théorie de la fiabilité dans la conception du produit afin de réduire la probabilité de défaillance. La probabilité de défaillance est aussi étroitement associé avec le produit de garantie.
Rapport à l'aléatoire
Dans un univers déterministe basé sur Newton concepts, il n'y a aucune probabilité si toutes les conditions sont connues. Dans le cas d'une roue de roulette, si la force de la main et la période de cette force sont connus, le numéro sur lequel la bille se arrêtera serait une certitude. Bien sûr, cela suppose également une connaissance de l'inertie et le frottement de la roue, le poids, la douceur et la rondeur de la balle, les variations de vitesse de la main au cours de la rotation et ainsi de suite. Une description probabiliste peut donc être plus utile que la mécanique newtonienne pour analyser la tendance des résultats de rouleaux répétées de roulette. Les physiciens sont confrontés à la même situation théorie cinétique des gaz, où le système, tandis que déterministe, en principe, est si complexe (avec le nombre de molécules généralement de l'ordre de grandeur de constante d'Avogadro ( 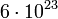 ) Que seule description statistique de ses propriétés est faisable.
) Que seule description statistique de ses propriétés est faisable.
Une découverte révolutionnaire de la physique du 20ème siècle était le caractère aléatoire de tous les processus physiques qui se produisent à l'échelle microscopique et sont régis par les lois de la mécanique quantique . Le fonction d'onde se évolue de manière déterministe tant qu'aucune observation est faite, mais, selon la vigueur Interprétation de Copenhague, le caractère aléatoire causée par la fonction d'onde se effondrer quand une observation est faite, est fondamentale. Cela signifie que la théorie des probabilités est nécessaire pour décrire la nature. D'autres ne sont jamais venus à des peines avec la perte du déterminisme. Albert Einstein célèbre fait remarquer dans une lettre à Max Born: jedenfalls bin ich überzeugt, dass der Alte nicht würfelt (Je suis convaincu que Dieu ne joue pas aux dés).. Bien que les points de vue différents existent, comme celle de décohérence quantique être la cause d'un effondrement aléatoire apparente, à l'heure actuelle il ya un consensus solide parmi les physiciens que la théorie des probabilités est nécessaire de décrire les phénomènes quantiques.
Citations
- Damon Runyon, "Il se peut que la course ne est pas toujours aux agiles, ni la bataille de la forte - mais ce est la façon de parier."
- Pierre-Simon Laplace "Il est remarquable que la science qui a commencé avec la prise en compte des jeux de hasard aurait dû devenir l'objet le plus important de la connaissance humaine." Théorie Analytique des Probabilités, 1812.
- Richard von Mises "L'extension illimitée de la validité des sciences exactes est un trait caractéristique de la rationalisme exagérée du XVIIIe siècle" (en référence à Laplace). Probabilités, Statistiques, et la Vérité, p 9. édition Dover, 1981 (réédition la deuxième édition anglaise, 1957).