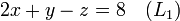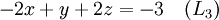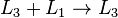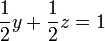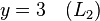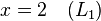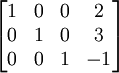Élimination de Gauss

En algèbre linéaire , élimination de Gauss est une algorithme qui peut être utilisé pour déterminer les solutions d'un système d'équations linéaires , de trouver la un rang de matrice , et pour calculer l'inverse d'un matrice carrée inversible. Élimination de Gauss est nommé d'après le mathématicien et scientifique allemand Carl Friedrich Gauss .

Opérations élémentaires sur les lignes sont utilisées dans l'algorithme. L'algorithme comporte deux parties, dont chacun considère les lignes de la matrice dans l'ordre. La première partie réduit la matrice Matrice échelonnée tandis que le second réduit la matrice à la suite de forme réduite de Gauss. La première partie seule est suffisante pour de nombreuses applications.

Un algorithme connexes, mais moins efficace, Gauss-Jordan élimination, apporte une matrice à forme réduite de Gauss en un seul passage.

Histoire

La méthode d'élimination de Gauss apparaît dans le chapitre huit, rectangulaires tableaux, de l'importante chinoise texte mathématique ou Jiuzhang suanshu Les Neuf Chapitres sur l'art mathématique. Son utilisation est illustrée sur dix-huit problèmes, de deux à cinq équations. La première référence à l'ouvrage de ce titre est daté à 179 CE, mais certaines parties ont été écrites dès environ 150 BCE.

Cependant, la méthode a été inventée en Europe indépendamment. Il est nommé d'après le mathématicien Carl Friedrich Gauss .

Aperçu Algorithme

Le processus d'élimination gaussienne comporte deux parties. La première partie (avant élimination) réduit un système donné soit triangulaire ou forme échelonnée, ou les résultats dans un équation dégénéré sans solution, indiquant que le système n'a pas de solution. Ceci est accompli par l'utilisation de opérations élémentaires sur les lignes. Les utilisations seconde étape substitution en arrière pour trouver la solution du système ci-dessus.

Déclaré équivalente pour les matrices, la première partie réduit à une matrice rangée forme échelon aide opérations élémentaires sur les lignes tandis que le second, il se réduit à forme réduite de Gauss, ou ramer forme canonique.

Un autre point de vue, qui se avère être très utile d'analyser l'algorithme, ce est que l'élimination de Gauss calcule une matrice décomposition. Les trois opérations élémentaires sur les lignes utilisées dans l'élimination de Gauss (multiplication de lignes, la commutation de lignes, et en ajoutant un multiple de lignes à d'autres lignes) montant à la multiplication de la matrice d'origine avec des matrices inversibles de la gauche. La première partie de l'algorithme calcule une LU décomposition, tandis que la deuxième partie écrit la matrice d'origine comme le produit d'une matrice inversible uniquement déterminé et un réduit matrice rangée échelonnée uniquement déterminée.

Exemple

Supposons que le but est de trouver et de décrire la solution (s), le cas échéant, de ce qui suit système d'équations linéaires :

L'algorithme est le suivant: à éliminer 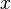à partir de toutes les équations ci-dessous 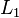, Puis éliminer à partir de toutes les équations ci-dessous . Cela mettra le système en forme triangulaire. Puis, en utilisant de nouveau la substitution, chaque inconnu peut être résolue pour.

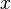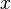Dans notre exemple, nous éliminons à partir de en ajoutant à , Puis nous éliminons à partir de 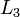en ajoutant 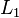à 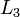. Formellement:

Le résultat est le suivant:

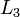Maintenant, nous éliminons à partir de en ajoutant 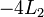à :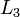

Le résultat est le suivant:

Ce résultat est un système d'équations linéaires en forme triangulaire, de sorte que la première partie de l'algorithme est terminé.

La deuxième partie, back-substitution, consiste à résoudre pour les inconnues dans l'ordre inverse. Ainsi, nous pouvons facilement voir que

Ensuite, 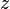peut être substitué en , Qui peut ensuite être résolu facilement obtenir

Suivan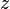t, et peut être substitué en 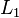, Qui peut être réglé pour obtenir

Ainsi, le système est réglé.

Cet algorithme fonctionne pour ne importe quel système d'équations linéaires. Il est possible que le système ne peut pas être réduite à la forme triangulaire, mais toujours avoir au moins une solution valable: par exemple, si ne est pas survenu dans et 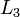après notre première étape ci-dessus, l'algorithme aurait été incapable de réduire le système à la forme triangulaire. Toutefois, il serait encore réduit le système de forme échelonnée. Dans ce cas, le système n'a pas de solution unique, car il contient au moins un variable libre. L'ensemble de la solution peut alors être exprimé paramétrique (ce est, en termes de variables libres, de sorte que si les valeurs pour les variables libres sont choisis, une solution sera généré).

En pratique, on ne traite pas habituellement avec les systèmes réels en termes des équations, mais fait plutôt l'utilisation de la matrice augmentée (ce qui est également approprié pour des manipulations informatiques). Ce, alors, est l'algorithme gaussien appliqué à l'élimination augmentée matrice du système ci-dessus, commençant par:

qui, à la fin de la première partie de l'algorithme se présente comme suit:

Ce est à dire qu'il se trouve dans formulaire de Gauss.

A la fin de l'algorithme, on se retrouve avec

Ce est à dire qu'il se trouve dans forme réduite de Gauss de, ou la ligne forme canonique.

D'autres applications

Trouver l'inverse d'une matrice

Supposer 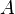est un Matrix et vous avez besoin de calculer sa inverse. Le matrice d'identité est augmentée vers la droite de 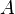, Formant une 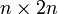matrice (le matrice de bloc ). Grâce à l'application des opérations élémentaires sur les lignes et l'algorithme d'élimination gaussienne, le bloc de gauche de peut être réduite à la matrice d'identité , Ce qui laisse dans le bloc de droite de .

Si l'algorithme est incapable de réduire 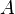à la forme triangulaire, puis 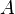ne est pas inversible.

Dans la pratique, inversant une matrice est rarement nécessaire. La plupart du temps, on ne est vraiment après que la solution d'un système d'équations linéaires particulier.

L'algorithme général pour calculer les rangs et bases

L'algorithme d'élimination gaussienne peut être appliquée à ne importe quel 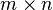matrice 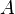. Si nous obtenons «coincés» dans une colonne donnée, nous passons à la colonne suivante. De cette façon, par exemple, certaines 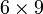matrices peuvent être transformés en une matrice qui a une rangée forme échelonnée réduite comme

(Les * s 'sont des entrées arbitraires). Cette matrice d'échelon contient une mine d'informations sur 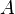: Le rang de 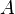est 5 car il existe cinq rangées non nulles dans ; l' espace vectoriel engendré par les colonnes de 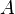a une base constituée de la première, troisième, quatrième, septième et neuvième colonne de 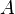(les colonnes de celles de ), Et le * 's vous dire comment les autres colonnes de 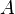peut se écrire comme des combinaisons linéaires des colonnes de base.

Analyse

Élimination de Gauss sur une matrice n × n nécessite environ 2 n ^3/3 opérations. Donc, il a une complexité de .

Cet algorithme peut être utilisé sur un ordinateur pour les systèmes avec des milliers d'équations et d'inconnues. Cependant, le coût devient prohibitif pour les systèmes avec des millions d'équations. Ces grands systèmes sont généralement résolus en utilisant méthodes itératives. Méthodes spécifiques existent pour les systèmes dont les coefficients suivent un schéma régulier (voir système d'équations linéaires ).

L'élimination de Gauss peut être effectuée sur tout domaine.

Élimination de Gauss est numériquement stable pour diagonale dominante ou matrices définies positives. Pour les matrices générales, élimination de Gauss est généralement considéré comme stable dans la pratique si vous utilisez pivot partiel tel que décrit ci-dessous, même si il ya des exemples pour lesquels il est instable.

Pseudocode

Comme expliqué ci-dessus, l'élimination de Gauss écrit une donnée m × n matrice A uniquement comme un produit d'un m × m inversible matrice S et une matrice de Gauss T. Ici, S est le produit des matrices correspondant aux opérations effectuées en rangée.

L'algorithme pour calculer formelle à partir de 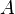suit. Nous écrivons pour l'entrée dans la rangée , Colonne 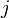en matrice 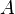. La transformation est effectuée «en place», ce qui signifie que la matrice originale 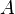est perdu et successivement remplacé par .

i := 1 j := 1 while (i ≤ m and j ≤ n) do Find pivot in column j, starting in row i: maxi := i for k := i+1 to m do if abs(A[k,j]) > abs(A[maxi,j]) then maxi := k end if end for if A[maxi,j] ≠ 0 then swap rows i and maxi, but do not change the value of i Now A[i,j] will contain the old value of A[maxi,j]. divide each entry in row i by A[i,j] Now A[i,j] will have the value 1. for u := i+1 to m do subtract A[u,j] * row i from row u Now A[u,j] will be 0, since A[u,j] - A[i,j] * A[u,j] = A[u,j] - 1 * A[u,j] = 0. end for i := i + 1 end if j := j + 1 end while 

Cet algorithme diffère légèrement de celui évoqué plus tôt, parce que avant d'éliminer une variable, il échange des premières rangées pour déplacer l'entrée avec la plus grande valeur absolue à la "position de pivot". Tel que procédure de pivotement permet d'améliorer la stabilité numérique de l'algorithme; certaines variantes sont également en cours d'utilisation.

La colonne en cours de transformation est appelée la colonne de pivotement. Procédez de gauche à droite, laissant la colonne pivot soit la première colonne, puis la deuxième colonne, etc. et enfin la dernière colonne avant la ligne verticale. Pour chaque colonne pivot, faire les deux étapes suivantes avant de passer à la colonne pivot suivante:

1. Recherchez l'élément en diagonale dans la colonne de pivot. Cet élément est appelé pivot. La ligne contenant le pivot est appelé la ligne de pivot. Diviser chaque élément de la ligne pivot par le pivot d'obtenir une nouvelle ligne de pivot avec un 1 dans la position de pivot.
2. Obtenir un 0 à chaque position au-dessous de la position de pivotement en soustrayant un multiple approprié de la ligne de pivotement de chacune des rangées au-dessous.

À l'issue de cette procédure, la matrice augmentée sera en forme échelonnée et peut être résolu en arrière-substitution.