Carl Friedrich Gauss

Carl Friedrich Gauss
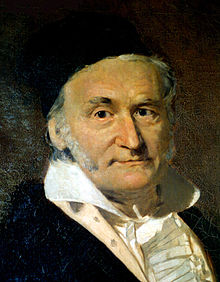Carl Friedrich Gauss (1777-1855), peint par Christian Albrecht Jensen
Né	(30/04/1777) 30 Avril 1777 Braunschweig, Duché de Brunswick-Wolfenbüttel, Saint-Empire romain
Mort	23 Février 1855 (23/02/1855) (77 ans) Göttingen, Royaume de Hanovre
Résidence	Royaume de Hanovre
Nationalité	Allemand
Les champs	Mathématiques et physique
Institutions	Université de Göttingen
Alma mater	Université de Helmstedt
Conseiller de doctorat	Johann Friedrich Pfaff
Autres conseillers pédagogiques	Johann Christian Martin Bartels
Doctorants	Friedrich Bessel Christoph Gudermann Christian Ludwig Gerling Richard Dedekind Johann Encke Johann Annonce Bernhard Riemann Christian Peters Moritz Cantor
D'autres étudiants remarquables	Johann Dirichlet Gotthold Eisenstein Carl Wolfgang Benjamin Goldschmidt Gustav Kirchhoff Ernst Kummer Août Ferdinand Möbius LC Schnürlein Julius Weisbach
Connu pour	Voir la liste complète
Influencé	Sophie Germain
Prix remarquables	Médaille Copley (1838)
Signature

Johann Carl Friedrich Gauss (pron .: / ɡ aʊ s /; allemande : Gauss, prononcée [ɡaʊs]; latine : Carolus Fridericus Gauss) (30 Avril 1777 au 23 Février 1855) était un Allemand mathématicien et physicien qui ont contribué de manière significative à de nombreux domaines, y compris la théorie des nombres , l'algèbre , statistiques , analyse , géométrie différentielle , géodésie, géophysique, électrostatique, l'astronomie et l'optique .

Parfois dénommé Mathematicorum Princeps ( latine , "le prince des mathématiciens» ou «le premier des mathématiciens») et «plus grand mathématicien depuis l'antiquité", Gauss a eu une influence remarquable dans de nombreux domaines des mathématiques et de la science et se classe comme l'un des mathématiciens les plus influents de l'histoire. Il se est référé aux mathématiques comme «la reine des sciences».

Les premières années (1777-1798)

Statue de Gauss dans sa ville natale, Braunschweig

Carl Friedrich Gauss est né le 30 Avril 1777 à Braunschweig (Brunswick), dans le Duché de Braunschweig-Wolfenbüttel, fait maintenant partie de Basse-Saxe, Allemagne , comme le fils de parents pauvres de la classe ouvrière. En effet, sa mère était analphabète et n'a jamais enregistré la date de sa naissance, se souvenant seulement qu'il était né un mercredi, huit jours avant la Fête de l'Ascension, qui se se produit 40 jours après Pâques . Gauss plus tard résoudre ce puzzle sur sa date de naissance dans le contexte de trouver la date de Pâques, l'établissement de méthodes pour calculer la date dans les deux années passées et futures. Il a été baptisé et confirmé dans une église près de l'école il a assisté comme un enfant.

Gauss était enfant prodige. Il existe de nombreuses anecdotes sur sa précocité tandis qu'un enfant en bas âge, et il a fait ses premières découvertes mathématiques révolutionnaires alors qu'il était encore adolescent. Il a complété Disquisitiones Arithmeticae, son magnum opus, en 1798 à l'âge de 21 ans, se il n'a pas été publié jusqu'en 1801. Ce travail a été fondamental dans la consolidation de la théorie des nombres en tant que discipline et a façonné le champ à nos jours.

Capacités intellectuelles de Gauss ont attiré l'attention de la Duc de Brunswick, qui l'a envoyé à l'Collegium Carolinum (maintenant Technische Universität Braunschweig), auquel il a assisté de 1792 à 1795, et à la Université de Göttingen de 1795 à 1798. Pendant son séjour à l'université, Gauss redécouvert indépendamment plusieurs théorèmes importants; sa percée a eu lieu en 1796 quand il a montré que toute régulier polygone avec un nombre de côtés qui est un Fermat premier (et, par conséquent, ces polygones avec ne importe quel nombre de côtés qui est le produit de nombres premiers de Fermat distincts et une puissance de 2) peut être construit en règle et au compas . Ce était une découverte majeure dans un domaine important des mathématiques; problèmes de construction avaient occupé les mathématiciens depuis l'époque des Grecs anciens , et la découverte de Gauss a finalement conduit à choisir les mathématiques au lieu de philologie comme une carrière. Gauss était si heureux de ce résultat qu'il a demandé qu'un régulière Heptadécagone être inscrit sur sa pierre tombale. Le maçon a refusé, disant que la construction serait difficile essentiellement ressembler à un cercle.

L'année 1796 a été la plus productive pour les deux Gauss et la théorie des nombres. Il a découvert une construction de la Heptadécagone le 30 Mars. Il se avança encore arithmétique modulaire , ce qui simplifie grandement les manipulations en théorie des nombres. Le 8 Avril, il est devenu le premier à prouver la la loi de réciprocité quadratique. Cette loi permet mathématiciens remarquablement générale pour déterminer la solvabilité d'une équation quadratique en arithmétique modulaire. Le théorème des nombres premiers, conjecturé le 31 mai, donne une bonne compréhension de la façon dont les nombres premiers sont répartis entre les nombres entiers. Gauss a également découvert que chaque nombre entier positif est représentable comme la somme d'au plus trois nombres triangulaires le 10 Juillet et puis notaient dans son journal la fameuse note: " ΕΥΡΗΚΑ! num = Δ + Δ + Δ ". Le 1er Octobre, il a publié un résultat sur le nombre de solutions de polynômes à coefficients dans les corps finis, qui ont conduit 150 ans plus tard à la Conjectures de Weil.

Moyen années (1799-1830)

Dans son doctorat en 1799 contumace, une nouvelle preuve du théorème que chaque fonction algébrique rationnelle intégrante d'une variable peut être résolu en facteurs réels du premier ou du second degré, Gauss a prouvé la théorème fondamental de l'algèbre qui stipule que chaque seule variable non constante polynôme à coefficients complexes a au moins un complexe racine. Les mathématiciens y compris Jean le Rond d'Alembert avait produit de fausses preuves devant lui, et la dissertation de Gauss contient une critique du travail de d'Alembert. Ironie du sort, par le niveau d'aujourd'hui, propre tentative de Gauss ne est pas acceptable, en raison de l'utilisation implicite de la Théorème de Jordan. Toutefois, il a produit par la suite trois autres preuves, le dernier en 1849 étant généralement rigoureux. Ses tentatives de clarifier le concept des nombres complexes considérablement le long du chemin.

Gauss a également fait d'importantes contributions à la théorie des nombres avec son livre 1801 Disquisitiones Arithmeticae ( latine , arithmétiques enquêtes), qui, parmi les choses, introduit le symbole ≡ la congruence et utilisé dans une présentation propre de l'arithmétique modulaire , contenait les deux premières épreuves de la loi du réciprocité quadratique, développé les théories de binaires et ternaires formes quadratiques, a déclaré le classe problème de nombre pour eux, et a montré qu'un régulière Heptadécagone (polygone de 17 côtés) peut être construit avec règle et le compas .

Page de titre de Gauss Disquisitiones Arithmeticae

Dans la même année, italienne astronome Giuseppe Piazzi a découvert le planète naine Cérès . Piazzi ne pouvait suivre Ceres pendant quelques mois, à la suite pour trois degrés dans le ciel de nuit. Puis il a disparu temporairement derrière l'éclat du Soleil Plusieurs mois plus tard, quand Ceres auraient réapparu, Piazzi ne pouvait pas le localiser: les outils mathématiques de l'époque ne étaient pas en mesure d'extrapoler une position d'une telle quantité de données peu-trois degrés représentent moins de 1% de l'orbite totale.

Gauss, qui avait 23 ans à l'époque, a entendu parler du problème et qu'il a abordé. Après trois mois de travail intense, il a prédit une position pour Ceres en Décembre 1801, juste un an après sa première observation et cela se est avéré être précis dans un demi-degré quand il a été redécouvert par Franz Xaver von Zach le 31 Décembre au Gotha, et un jour plus tard par Heinrich Olbers dans Brême.

La méthode de Gauss a consisté à déterminer une section conique dans l'espace, étant donné une mise au point (le Soleil) et l'intersection de la conique avec trois lignes données (lignes de vue de la Terre, qui est lui-même le déplacement sur une ellipse, à la planète) et étant donné le temps qu'il prend la planète à traverser les arcs déterminées par ces lignes (à partir de laquelle les longueurs des arcs peuvent être calculés par la deuxième loi de Kepler). Ce problème conduit à une équation du huitième degré, dont une solution, l'orbite de la Terre, est connue. La solution recherché est ensuite séparé de la six restants sur la base de conditions physiques. Dans ce travail, Gauss a utilisé des méthodes d'approximation complets qu'il a créé à cette fin.

Un tel procédé est le transformée de Fourier rapide. Bien que cette méthode est traditionnellement attribué à un document 1965 par JW Cooley et JW Tukey, Gauss développé comme une méthode d'interpolation trigonométrique. Son papier, Theoria Interpolationis Methodo Nouvelle Tractata, ne fut publié à titre posthume dans le volume 3 de ses œuvres complètes. Ce document est antérieur à la première présentation par Joseph Fourier sur le sujet en 1807.

Zach a noté que «sans le travail intelligent et calculs du docteur Gauss nous ne aurions pas trouvé Ceres nouveau". Bien que Gauss avait jusque-là été soutenu financièrement par son traitement du duc, il douté de la sécurité de cet arrangement, et n'a pas non plus croire que les mathématiques pures pour être suffisamment important pour mériter l'appui. Ainsi il a cherché une position dans l'astronomie, et en 1807 a été nommé professeur d'astronomie et directeur de l'astronomie observatoire de Göttingen, un poste qu'il a occupé pendant le reste de sa vie.

La découverte de Cérès conduit Gauss à son travail sur une théorie du mouvement des planétoïdes perturbé par de grandes planètes, éventuellement publiées en 1809 comme Theoria motus corporum coelestium dans sectionibus conicis solem Ambientum (théorie du mouvement des corps célestes se déplaçant dans les sections coniques autour de la Sun). Dans le processus, il le rationalisé les mathématiques lourdeur de prévision orbitale du 18ème siècle que son travail demeure une pierre angulaire du calcul astronomique. Il a introduit le Constante gravitationnelle gaussien, et contenait un traitement influent de la méthode des moindres carrés , une procédure utilisée dans toutes les sciences à ce jour afin de minimiser l'impact de l'erreur de mesure. Gauss a prouvé la méthode dans l'hypothèse d' une distribution normale des erreurs (voir Théorème de Gauss-Markov; voir aussi Gaussienne). Le procédé a été décrit précédemment par Adrien-Marie Legendre en 1805, mais Gauss affirmé qu'il avait été utilisé depuis 1795.

Le portrait de Gauss publié en Astronomische Nachrichten 1828

En 1818, Gauss, mettant ses compétences de calcul en pratique, réalisé une géodésiques de la Royaume de Hanovre, le lien avec les précédents danois enquêtes. Pour aider l'enquête, Gauss a inventé le héliotrope, un instrument qui utilise un miroir pour refléter la lumière du soleil sur de grandes distances, pour mesurer les positions.

Gauss a également affirmé avoir découvert la possibilité de géométries non-euclidiennes, mais jamais publié il. Cette découverte a été un changement de paradigme majeur dans les mathématiques, car il a libéré les mathématiciens de la croyance erronée que les axiomes d'Euclide étaient le seul moyen de faire la géométrie cohérente et non contradictoire. La recherche sur ces géométries conduit, entre autres choses, Einstein la théorie de la relativité générale, qui décrit l'univers comme non-euclidienne. Son ami Farkas Wolfgang Bolyai avec qui Gauss avait juré "la fraternité et la bannière de la vérité" en tant qu'étudiant, avait essayé en vain pendant de nombreuses années pour prouver le postulat parallèle auprès d'autres axiomes de la géométrie d'Euclide. Le fils de Bolyai, János Bolyai, découvrit géométrie non-euclidienne en 1829; son travail a été publié en 1832. Après l'avoir vu, Gauss écrivit à Farkas Bolyai: "Pour l'éloge reviendrait à me louer Pour l'ensemble du contenu de l'œuvre ... coïncide presque exactement avec mes propres méditations qui ont occupé mon esprit. les trente ou trente-cinq dernières années. "

Quatre distributions gaussiennes dans les statistiques

Cette déclaration non prouvée mis une pression sur sa relation avec János Bolyai (qui pensait que Gauss a été "volé" son idée), mais il est maintenant généralement prises à leur valeur nominale. Lettres de Gauss années avant 1829 révèlent lui obscurément discuter le problème de lignes parallèles. Waldo Dunnington, un biographe de Gauss, plaide en Gauss, Titan de la science que Gauss était en fait en pleine possession de géométrie non-euclidienne longtemps avant qu'il a été publié par János Bolyai, mais qu'il a refusé de publier quoi que ce soit à cause de sa peur de la controverse.

L'enquête de Hanovre a alimenté l'intérêt de Gauss dans la géométrie différentielle , un domaine des mathématiques traitant de courbes et surfaces. Entre autres choses, il est venu avec la notion de Courbure gaussienne. Cela a conduit en 1828 à un théorème important, le Theorema egregium (théorème remarquable), instituant une propriété importante de la notion de courbure. De façon informelle, le théorème dit que la courbure d'une surface peut être déterminée entièrement par la mesure des angles et des distances sur la surface. Ce est-à courbure ne dépend pas de la façon dont la surface peut être incorporé dans l'espace à 3 dimensions ou espace 2 dimensions.

En 1821, il a été nommé membre étranger de la Académie royale des sciences de Suède.

Ans plus tard, la mort (1831-1855)

Daguerréotype de Gauss sur son lit de mort, 1855.

Grave de Gauss au Albanifriedhof dans Göttingen, Allemagne .

En 1831, Gauss a développé une collaboration fructueuse avec le professeur de physique Wilhelm Weber, conduisant à de nouvelles connaissances dans le magnétisme (y compris trouver une représentation pour l'unité du magnétisme en termes de masse, de longueur et de temps) et la découverte de Lois de Kirchhoff de l'électricité. Ce est durant cette période qu'il a formulé son homonyme loi . Ils ont construit le premier télégraphe électromécanique en 1833, qui reliait l'observatoire avec l'institut de physique à Göttingen. Gauss a ordonné un champ magnétique observatoire pour être construit dans le jardin de l'observatoire, et avec Weber a fondé le "Magnetischer Verein" (club magnétique dans allemand ), qui a soutenu les mesures du champ magnétique de la Terre dans de nombreuses régions du monde. Il a développé une méthode de mesure de l'intensité horizontale du champ magnétique qui était en usage jusque dans la seconde moitié du 20ème siècle, et a travaillé sur la théorie mathématique pour séparer l'intérieur et extérieur ( magnétosphère) sources du champ magnétique de la Terre.

En 1840, Gauss a publié son influent Dioptrische Untersuchungen, dans lequel il a donné la première analyse systématique sur la formation d'images sous un approximation paraxiale ( Optique de type Gauss). Parmi ses résultats, Gauss a montré que, dans une approximation paraxiale un système optique peut être caractérisé par son points cardinaux et il dérivés de la formule de la lentille de Gauss.

En 1854, Gauss notamment choisi le thème de Bernhard Riemann s 'désormais célèbre Habilitationvortrag, Über die Hypothesen, welche der Geometrie zu Grunde liegen. Sur le chemin du retour de la conférence de Riemann, Weber a indiqué que Gauss était plein d'éloges et d'excitation.

Gauss est mort à Göttingen, dans le Royaume de Hanovre (maintenant partie de Basse-Saxe, Allemagne) en 1855 et est enterré dans le Albanifriedhof cimetière là. Deux individus ont donné des éloges à son enterrement: Gauss fils-frère Heinrich Ewald et Wolfgang von Waltershausen Sartorius, qui était proche ami et biographe de Gauss. Son cerveau a été conservé et a été étudié par Rudolf Wagner qui a trouvé sa masse soit 1492 grammes et la zone cérébrale égal à 219 588 millimètres carrés (340,362 pouces carrés). Circonvolutions très développés ont également été trouvés, ce qui dans le début du 20e siècle a été suggéré que l'explication de son génie.

Religion

Bühler écrit que, selon la correspondance avec Rudolf Wagner, Gauss ne semble pas croire en un dieu personnel. Il a été dit être un déiste. Il affirme en outre que, bien que Gauss croyait fermement en l'immortalité de l'âme et en quelque sorte de la vie après la mort, ce ne était pas d'une manière qui pourrait être interprétée comme chrétienne.

Selon Dunnington, la religion de Gauss a été basée sur la recherche de la vérité. Il croyait en "l'immortalité de l'individualité spirituelle, dans une permanence personnelle après la mort, dans un dernier ordre des choses, dans un Dieu éternel, juste, omniscient et omnipotent". Gauss a également confirmé la tolérance religieuse, croyant à tort déranger les autres qui étaient en paix avec leurs propres croyances.

Famille

Gauss de la fille Thérèse (1816-1864)

Vie personnelle de Gauss a été éclipsé par la mort prématurée de sa première femme, Johanna Osthoff, en 1809, bientôt suivi par la mort d'un enfant, Louis. Gauss plongé dans une la dépression à partir de laquelle il n'a jamais complètement récupéré. Il se est marié à nouveau, au meilleur ami de Johanna nommé Friederica Wilhelmine Waldeck mais communément connu comme Minna. Quand sa seconde épouse est décédée en 1831 après une longue maladie, une de ses filles, Thérèse, a repris le ménage et soignés Gauss jusqu'à la fin de sa vie. Sa mère a vécu dans sa maison de 1817 jusqu'à sa mort en 1839.

Gauss avait six enfants. Avec Johanna (1780-1809), ses enfants étaient Joseph (1806-1873), Wilhelmina (1808-1846) et Louis (1809-1810). De tous les enfants de Gauss, Wilhelmina a dit être venu plus proche de son talent, mais elle est morte jeune. Avec Minna Waldeck il a également eu trois enfants: Eugène (1811-1896), Wilhelm (1813-1879) et Thérèse (1816-1864). Eugene partagé une bonne mesure du talent de Gauss en langues et calcul. Thérèse tenait la maison pour Gauss jusqu'à sa mort, après quoi elle se est mariée.

Gauss a finalement dû conflits avec ses fils. Il ne voulait pas de ses fils pour entrer mathématiques ou les sciences pour "peur de l'abaissement du nom de famille". Gauss voulait Eugene pour devenir un avocat, mais Eugène voulait étudier les langues. Ils avaient un argument sur une partie Eugene lieu, qui Gauss a refusé de payer. Le fils a quitté dans la colère et, dans environ 1832, a émigré aux États-Unis, où il était tout à fait réussie. Wilhelm a également réglé dans Missouri, en commençant par un fermier et plus tard, devenir riche dans le domaine de la chaussure dans St. Louis. Il a fallu de nombreuses années pour le succès de Eugene pour contrecarrer sa réputation parmi les amis et collègues de Gauss. Voir également la lettre de Robert Gauss à Félix Klein le 3 Septembre 1912.

Personnalité

Gauss était un ardent perfectionniste et un travailleur acharné. Il n'a jamais été un écrivain prolifique, refusant de publier des travaux dont il n'a pas jugé complet et dessus de toute critique. Ce était conforme à sa devise personnelle pauca de matura sed ("quelques-uns, mais mûrs"). Ses journaux intimes indiquent qu'il avait fait plusieurs années ou décennies des découvertes mathématiques importantes avant ses contemporains les publier. Historien mathématique Eric Temple Bell a estimé que, si Gauss publié tous ses découvertes en temps opportun, il aurait avancé mathématiques en cinquante ans.

Bien qu'il ne prenne en quelques étudiants, Gauss a été connu pour ne pas aimer l'enseignement. Il est dit qu'il a assisté à une seule conférence scientifique, qui était dans Berlin en 1828. Cependant, plusieurs de ses étudiants est devenu mathématiciens influents, parmi eux Richard Dedekind, Bernhard Riemann , et Friedrich Bessel. Avant de mourir, Sophie Germain a été recommandé par Gauss pour recevoir son diplôme honorifique.

Gauss généralement refusé de présenter l'intuition derrière ses souvent très élégantes preuves-il les préférait à apparaître "à partir de rien" et effacé toutes les traces de la façon dont il les a découverts. Cela se justifie, si insatisfaisante, par Gauss dans son " Disquisitiones Arithmeticae ", où il affirme que toutes les analyses (ce est à dire, les chemins une parcourir pour atteindre la solution d'un problème) doit être supprimée par souci de brièveté.

Gauss a soutenu la monarchie et se oppose à Napoléon , qu'il voyait comme une excroissance de la révolution .

Anecdotes

Il ya plusieurs histoires de son début de génie. Selon un, ses dons sont devenus très apparente à l'âge de trois ans quand il a corrigé, mentalement et sans faute dans ses calculs, une erreur son père avait fait sur le papier tout en calculant les finances.

Un autre célèbre histoire veut que dans l'école primaire après que le jeune Gauss se conduit mal, son professeur, JG Büttner, lui a donné une tâche: ajouter une liste de nombres entiers dans progression arithmétique; que l'histoire est le plus souvent dit, ce sont les nombres de 1 à 100. Le jeune Gauss produit réputé la bonne réponse en quelques secondes, à l'étonnement de son professeur et son assistant Martin Bartels.

Méthode présumée de Gauss était de réaliser que l'addition par paire de termes à partir des extrémités opposées de la liste sommes intermédiaires donnaient identiques: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, et ainsi de suite, pour un montant total de 50 × 101 = 5050. Toutefois, les détails de l'histoire sont, au mieux, incertaine (voir la discussion de l'original Source de Wolfgang von Waltershausen Sartorius et les changements dans d'autres versions); certains auteurs, comme Joseph Rotman dans son livre Un premier cours de Abstract Algebra, se demandent se il ne se était passé.

Selon Isaac Asimov , Gauss a été une fois interrompu au milieu d'un problème et a dit que sa femme était en train de mourir. Il est censé avoir dit: «Dites-lui d'attendre un moment jusqu'à ce que je en ai fini." Cette anecdote est brièvement discutée dans Gauss G. Waldo Dunnington, Titan de la Science où il est suggéré que ce est un apocryphe histoire.

Commémorations

10- allemande Deutsche Mark billets (1993; abandonnées) avec Gauss

Gauss (âgé d'environ 26) sur Allemagne de l'Est timbre produite en 1977. A côté de lui: Heptadécagone, règle et au compas .

De 1989 à 2001, le portrait de Gauss, une courbe de distribution normale et certains de premier plan Göttingen bâtiments ont été présentés sur les dix-mark allemand billet. L'inverse en vedette le héliotrope et un approche de triangulation pour Hannover. L'Allemagne a également émis trois timbres honorant Gauss. Un (. 725 pas) est apparu en 1955 sur le centième anniversaire de sa mort; deux autres, nos. 1246 et 1811, en 1977, le 200e anniversaire de sa naissance.

2005 roman de Daniel Kehlmann Die Welt der Vermessung, traduit en anglais par Arpenteurs du monde (2006), explore la vie de Gauss et de travailler à travers une lentille de la fiction historique, les opposant à celles de l'explorateur allemand Alexander von Humboldt.

En 2007, un buste de Gauss a été placée dans le Temple Walhalla.

Choses nommées en l'honneur de Gauss comprennent:

• Démagnétisation, le processus d'élimination d'un champ magnétique.
• Le CGS Unité pour champ magnétique a été nommé gauss en son honneur,
• Le cratère Gauss sur la Lune ,
• Astéroïde 1001 Gaussia,
• Le bateau Gauss, utilisé dans la Gauss expédition en Antarctique,
• Mont Gauss, un volcan éteint découvert par l'expédition mentionnés ci-dessus,
• Gaußturm, une tour d'observation dans Dransfeld, l'Allemagne ,
• Dans les écoles secondaires de premier cycle canadiens, un concours annuel de mathématiques (concurrence mathématiques Gauss) administré par le Centre d'éducation en mathématiques et en informatique est nommé en l'honneur de Gauss,
• En Université de Californie, Santa Cruz, à College Couronne, un bâtiment dortoir est nommé d'après lui,
• Le Gauss Haus, un Centre RMN au Université de l'Utah,
• Le Carl-Friedrich-Gauß école pour les mathématiques, informatique, administration des affaires, économie et sciences sociales de Université de Braunschweig,
• Le bâtiment Gauss - Université de l'Idaho (College of Engineering).

En 1929, le Polonais mathématicien Marian Rejewski, qui permettrait de résoudre le allemand Enigma machine de chiffrement en Décembre 1932, a commencé à étudier statistiques actuarielles à Göttingen. À la demande de son Professeur à l'Université de Poznań, Zdzisław Krygowski, en arrivant à Göttingen Rejewski a déposé des fleurs sur la tombe de Gauss.

Écrits

• 1799: Thèse de doctorat sur la Théorème fondamental de l'algèbre, avec le titre: Demonstratio nova theorematis omnem functionem algebraicam rationalem INTEGRAM unius variabilis dans factores reales primi vel secundi gradus resolvi posse ("Nouvelle preuve du théorème que chaque fonction algébrique intégrante d'une variable peut être résolu en facteurs réels ( ce est à dire, les polynômes) du premier ou du deuxième degré ")
• 1801: Disquisitiones Arithmeticae. Traduction allemande par H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae et autres documents sur la théorie des nombres) (Deuxième édition). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 1-453. Traduction anglaise par Arthur A. Clarke Disquisitiones Arithemeticae (Deuxième édition, corrigée). New York: Springer. 1986. ISBN 0-387-96254-9.
• 1808: Theorematis arithmetici demonstratio nova. Göttingen: Commentaire. Soc. regiae sci, Göttingen XVI. Traduction allemande par H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae et autres documents sur la théorie des nombres) (Deuxième édition). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 457-462 [lance Lemme de Gauss, l'utilise dans la troisième preuve de réciprocité quadratique]
• 1809: Theoria Motus Corporum Coelestium dans sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne dans Kegelschnitten umkreisen), traduction anglaise par CH Davis, réimprimé 1963, Dover, New York.
• 1811: Summatio serierun quarundam singularium. Göttingen: Commentaire. Soc. regiae sci, Göttingen. Traduction allemande par H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae et autres documents sur la théorie des nombres) (Deuxième édition). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 463-495 [Détermination du signe de la quadratique somme de Gauss, utilise pour donner la quatrième preuve de réciprocité quadratique]
• 1812: Disquisitiones Generales Circa Seriem Infinitam
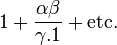
• 1818: Theorematis fundamentallis dans doctrina de residuis quadraticis demonstrationes et amplicationes novae. Göttingen: Commentaire. Soc. regiae sci, Göttingen. Traduction allemande par H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae et autres documents sur la théorie des nombres) (Deuxième édition). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 496-510 [Cinquième et sixième épreuves de réciprocité quadratique]
• 1821, 1823 et 1826: Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend die als Grundlage Wahrscheinlichkeitsrechnung des Gauß'schen Fehlerfortpflanzungsgesetzes. (Trois essais concernant le calcul des probabilités que la base de la loi gaussienne de propagation d'erreur) de traduction anglais par GW Stewart, 1987, Société pour les mathématiques industrielles.
• 1827: Disquisitiones generales circa superficies curvas, Commentationes societatis Regiae Scientiarum Gottingesis recentiores. Volume VI, pp. 99-146. " Enquêtes générales de surfaces courbes "(1965) publiés Raven Press, New York, traduits par AMHiltebeitel et JCMorehead.
• 1828: Theoria biquadraticorum de residuorum, Commentatio prima. Göttingen: Commentaire. Soc. regiae sci, Göttingen 6. traduction allemande par H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae et autres documents sur la théorie des nombres) (deuxième édition). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 511-533 [faits élémentaires sur résidus biquadratiques, prouve l'un des suppléments de la loi du la réciprocité biquadratique (le caractère biquadratique de 2)]
• 1832: Theoria biquadraticorum de residuorum, Commentatio secunda. Göttingen: Commentaire. Soc. regiae sci, Göttingen sept. Traduction allemand par H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae et autres documents sur la théorie des nombres) (deuxième édition). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 534-586 [lance le Entiers de Gauss, des États (sans preuve) de la loi la réciprocité biquadratique, prouve la loi supplémentaire pour 1 + i]
• 1843-1844: Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung, Abhandlungen der Gesellschaft der Wissenschaften Königlichen à Göttingen. Zweiter Band, pp. 3-46
• 1846-1847: Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung, Abhandlungen der Gesellschaft der Wissenschaften Königlichen à Göttingen. Dritter Band, pp. 3-44
• Mathematisches Tagebuch 1796-1814, Ostwaldts Klassiker, Harri Deutsch Verlag 2005, mit Anmerkungen von Neumamn, ISBN 978-3-8171-3402-1 (traduction anglaise avec annotations par Jeremy Gray:. Expositiones Math 1984)
• Œuvres collectives de Gauss sont en ligne ici, dont les traductions allemandes de textes latins et commentaires par diverses autorités