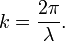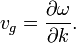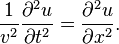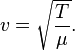Vague

Une vague est une perturbation qui se propage à travers l'espace et le temps , généralement avec le transfert de l'énergie . Alors une onde mécanique existe dans un moyen (déformation sur laquelle est capable de produire des forces de rappel élastiques), les ondes de rayonnement électromagnétique (et probablement rayonnement gravitationnel) peut voyager à travers vide, qui est, sans aucun support. Ondes se propagent et de transférer l'énergie d'un point à un autre, souvent avec peu ou pas de déplacement permanent des particules du milieu (ce est, avec peu ou pas de transport de masse associé); à la place il ya oscillations autour presque positions fixes.

Les ondes de surface dans l'eau

Définitions

Accord sur une définition unique et englobe tout pour l'onde terme est non négligeable. Un vibrations peut être définie comme un mouvement de va-et-vient autour d'un point m autour d'une valeur de référence. Cependant, définissant les caractéristiques nécessaires et suffisantes qui sont admissibles à un phénomène appelé une onde est, au moins, flexible. Le terme est souvent comprise intuitivement que le transport de perturbations dans l'espace, ne est pas associé avec le mouvement du milieu occuper cet espace comme un tout. Dans une vague, l' énergie d'un vibration se éloigne de la source sous la forme d'une perturbation dans le milieu environnant (Hall, 1980: 8). Toutefois, cette notion est problématique pour un onde stationnaire (par exemple, une vague sur une chaîne), où l'énergie se déplace dans les deux sens aussi, ou pour des ondes électromagnétiques / lumière dans un vide, où le concept de milieu ne se applique pas.

Pour ces raisons, la théorie des ondes représente une branche particulière de la physique qui est concerné par les propriétés de processus ondulatoires indépendamment de leur origine physique (Ostrovsky et Potapov, 1999). La particularité réside dans le fait que cette indépendance de l'origine physique se accompagne d'une forte dépendance sur l'origine pour décrire toute instance spécifique d'un processus d'onde. Par exemple, l'acoustique se distingue de l'optique dans que les ondes sonores sont liées à une mécanique plutôt qu'une ondes électromagnétiques comme le transfert / transformation de vibration énergétique . Des concepts tels que la masse , dynamique , inertie, ou élasticité, deviennent donc crucial dans la description acoustique (par opposition à optique) les procédés d'onde. Cette différence d'origine présente des caractéristiques particulières certain d'onde pour les propriétés du milieu impliqué (par exemple, dans le cas de l'air: les tourbillons, la pression de radiation, ondes de choc, etc., dans le cas des solides: Des ondes de Rayleigh, dispersion, etc., et ainsi de suite).

Autres propriétés, cependant, même se ils sont généralement décrits d'une manière spécifique d'origine, peuvent être généralisés à toutes les vagues. Par exemple, sur la base de l'origine mécanique des ondes acoustiques il peut y avoir une perturbation se déplaçant dans l'espace-temps si et seulement si le milieu ne est ni impliqué infiniment rigides ni infiniment souple. Si toutes les parties qui composent un milieu étaient strictement liés, ils seraient tous vibrer comme un seul, sans retard dans la transmission de la vibration et donc pas de mouvement de vague (ou mouvement des vagues plutôt infiniment rapide). D'autre part, si toutes les parties étaient indépendants, alors il n'y aurait pas de transmission de la vibration et encore, pas de mouvement d'onde (ou le mouvement des vagues plutôt infiniment lente). Bien que les énoncés ci-dessus ne ont aucun sens dans le cas des ondes qui ne nécessitent pas un milieu, ils révèlent une caractéristique qui est pertinent pour toutes les vagues indépendamment d'origine: dans une vague, le phase d'une vibration (ce est-à sa position dans le cycle de vibration) est différente pour les points adjacents dans l'espace, car la vibration atteint ces points à des moments différents.

De même, les processus d'ondes révélées par l'étude des phénomènes d'ondes avec des origines différentes de celle des ondes sonores peuvent être tout aussi importante à la compréhension des phénomènes sonores. Un exemple pertinent est le principe de Young d'interférence (Young, 1802, Hunt, 1978: 132). Ce principe a été introduit dans l'étude de Young, de la lumière et, dans certains contextes spécifiques (par exemple, la diffusion du son par son), est encore une zone de recherches dans l'étude du son.

Caractéristiques

Ondes périodiques sont caractérisées par écussons (sommets) et auges (plus bas), et peuvent généralement être classés comme soit longitudinale ou transversale. Ondes transversales sont ceux avec des vibrations perpendiculaires à la direction de la propagation de l'onde; exemples comprennent des vagues sur une chaîne et ondes électromagnétiques. Les ondes longitudinales sont ceux avec des vibrations parallèles à la direction de la propagation de l'onde; exemples comprennent vagues les plus sonores.

Quand un objet monte et descend sur une ondulation dans un étang, il éprouve une trajectoire orbitale parce ondulations ne sont pas simples ondes sinusoïdales transversales.

A = en eau profonde.
B = En eau peu profonde. Le mouvement circulaire d'une particule de surface devient elliptique avec la diminution de profondeur.
1 = Progression de la vague
2 = Crest
3 = Trough

Ondulations sur la surface d'un bassin sont en fait une combinaison d'ondes transversales et longitudinales; par conséquent, les points de la surface suivent des chemins orbitaux.

Tous les vagues ont un comportement commun en vertu d'un certain nombre de situations standard. Tous les vagues peuvent éprouver les suivantes:

• Réflexion - ondes changement de direction de frapper une surface réfléchissante
• Refraction - ondes changement de direction d'entrer dans un nouveau média
• circulaire d'onde propagation de pénétrer dans un trou d'une taille comparable à leurs longueurs d'onde - de diffraction
• Ingérence - superposition de deux ondes qui entrent en contact les uns avec les autres (en collision)
• fractionnement d'onde par la fréquence - de dispersion
• Propagation rectiligne - Le mouvement d'onde lumineuse dans une ligne droite

Polarisation

Une vague est polarisé se il ne peut osciller dans une direction. La polarisation d'une onde transverse décrit la direction d'oscillation dans le plan perpendiculaire à la direction de Voyage. Les ondes longitudinales telles que les ondes sonores ne présentent pas la polarisation, parce que ces ondes de la direction d'oscillation est le long de la direction de Voyage. Une vague peut être polarisée par l'utilisation d'un filtre polarisant.

Exemples

Une onde de surface de l'océan se écraser sur les rochers

Des exemples d'ondes comprennent:

• Océan ondes de surface, qui sont des perturbations qui se propagent dans l'eau.
• Les ondes radio, micro-ondes, les rayons infrarouges, la lumière visible , les rayons ultraviolets , des rayons X, et Les rayons gamma représentent un rayonnement électromagnétique . Dans ce cas, la propagation est possible sans un milieu, par le vide. Ces ondes électromagnétiques se déplacent à 299 792 458 m / s dans le vide.
• Son - une onde mécanique qui se propage dans l'air, liquide ou solide.
• vagues de la circulation (ce est-à propagation de différentes densités de véhicules à moteur, etc.) - ceux-ci peuvent être modélisés comme vagues cinématiques, comme le premier présenté par Sir MJ Lighthill
• Les ondes sismiques dans les tremblements de terre , dont il existe trois types, appelés S, P et L.
• Les ondes gravitationnelles, qui sont les fluctuations de la courbure de l'espace-temps prédites par la relativité générale . Ces ondes sont non linéaire, et doivent encore être observé empiriquement.
• Ondes d'inertie, qui se produisent dans les fluides tournants et restaurés par le Effet de Coriolis.

Description mathématique

Une vague d'amplitude constante.

Illustration d'une onde (la courbe bleue variant rapide) et son enveloppe (la courbe rouge variation plus lente).

D'un point de vue mathématique, la vague la plus primitive (ou fondamentale) est harmonique (sinusoïdales) onde qui est décrit par l'équation 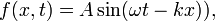où 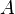est le amplitude d'une onde - une mesure de la perturbation maximale dans le milieu pendant un cycle d'onde (la distance maximale entre le point de la crête la plus élevée à l'équilibre). Dans l'illustration à droite, ce est la distance verticale maximale entre la ligne de base et la vague. Les unités de l'amplitude dépend du type de vague - ondes sur une chaîne ont une amplitude exprimée par une distance (m), les ondes sonores en tant que pression (Pa) et les ondes électromagnétiques que l'amplitude du champ électrique (Volts / mètre). L'amplitude peut être constante (dans ce cas, l'onde est une cw ou onde continue), ou peuvent varier avec le temps et / ou de position. La forme de la variation d'amplitude est appelé l'enveloppe de l'onde.

Le longueur d'onde (notée ) Est la distance entre deux crêtes successives (ou creux). Cela a généralement l'unité de mètres; il est aussi communément mesurée en nanomètre pour la partie optique de la spectre électromagnétique.

Un nombre d'onde peut être associée à la longueur d'onde par la relation

Les vagues peuvent être représentés par mouvement harmonique simple.

Le période Le temps est venu pour un cycle complet pour une oscillation d'une onde. Le fréquence (Également fréquemment désignée comme 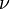) Est le nombre de périodes par unité de temps (par exemple une seconde) et est mesurée en hertz. Elles sont liées par:

En d'autres termes, la fréquence et la période d'une onde sont inverses les uns des autres.

Le fréquence angulaire 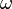représente la fréquence en termes de radians par seconde. Elle est liée à la fréquence par

Il existe deux vitesses qui sont associés à vagues. Le premier est le vitesse de phase, ce qui donne la vitesse à laquelle l'onde se propage, est donnée par

Le second est le vitesse de groupe, ce qui donne la vitesse à laquelle les variations de la forme de l'amplitude de l'onde se propagent à travers l'espace. Ce est la vitesse à laquelle l'information peut être transmise par l'onde. Elle est donnée par

L'équation d'onde

L'équation d'onde est une équation différentielle qui décrit l'évolution d'une onde harmonique au fil du temps. L'équation a des formes légèrement différentes selon la façon dont l'onde est transmise, et le milieu, il voyage à travers. Considérant une vague unidimensionnel qui se déplace vers le bas une corde le long de la axe des x avec une vitesse 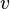et l'amplitude 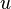(Qui dépend généralement de x et t), l'équation d'onde est

En trois dimensions, cela devient

où est le Laplace.

La vitesse v dépendra à la fois le type d'onde et le milieu à travers lequel il est transmis.

Une solution générale de l'équation des ondes dans une dimension est donnée par d'Alembert. C'est

Cela peut être considéré comme deux impulsions voyage long de la corde dans des directions opposées; F dans la direction + x, et G dans la - direction x. Si nous substituons x ci-dessus, le remplaçant par les directions x, y, z, nous avons ensuite pouvons décrire une onde se propageant dans les trois dimensions.

Le Équation de Schrödinger décrit le comportement ondulatoire des particules dans la mécanique quantique . Les solutions de cette équation sont fonctions d'onde qui peuvent être utilisés pour décrire la densité de probabilité d'une particule. La mécanique quantique décrit également des propriétés de particules que d'autres vagues, tels que la lumière et le son, ont à l'échelle atomique et au-dessous.

Ondes progressives

Simple vague ou onde progressive, parfois aussi appelé onde progressive est une perturbation qui varie à la fois avec le temps 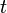et la distance 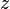de la manière suivante:

où est l'enveloppe d'amplitude de l'onde, est le nombre d'onde et est le phase. Le vitesse de phase v _p de cette onde est donnée par

où est le longueur d'onde de l'onde.

Onde stationnaire

Onde stationnaire dans un milieu stationnaire. Les points rouges représentent la vague nœuds

Une onde stationnaire, aussi connu comme une onde stationnaire, est une onde qui reste dans une position constante. Ce phénomène peut se produire parce que le support se déplace dans la direction opposée à la vague, ou il peut se produire dans un milieu stationnaire en raison de les interférences entre deux ondes se propageant dans des directions opposées.

La somme de deux ondes de contre-propagation (de même fréquence et amplitude) crée une onde stationnaire. Les ondes stationnaires surviennent souvent lorsqu'un blocs aux limites encore de propagation de l'onde, causant ainsi la réflexion des ondes, et en introduisant donc une vague de contre-propagation. Par exemple quand un violon chaîne est déplacé, ondes longitudinales se propagent à l'endroit où la chaîne est maintenu en place à la Bridge et de la " écrou ", où sur les ondes sont réfléchies. Au pont et" écrou ", les deux ondes opposées sont en opposition de phase et d'annuler l'autre, la production d'un noeud. A mi-chemin entre deux nœuds il ya une ventre, où les deux ondes contra-propagatives se renforcent mutuellement au maximum. Il est en moyenne pas de propagation net d'énergie.

Voir aussi: Résonance acoustique, Résonateur de Helmholtz, et tuyau d'orgue

Propagation à travers les chaînes

La vitesse d'une onde se propageant le long d'une corde vibrante (v) est directement proportionnelle à la racine carrée de la la tension (T) sur la densité linéaire (μ):

Support de transmission

Le support qui porte une onde se appelle un support de transmission. Il peut être classé dans l'une ou plusieurs des catégories suivantes:

• Un milieu linéaire si les amplitudes des différentes vagues à un moment précis dans le milieu peuvent être ajoutés.
• Un milieu bornée si elle est finie dans quelle mesure, sinon un milieu sans limite.
• Un milieu uniforme si ses propriétés physiques sont inchangées à différents endroits dans l'espace.
• Un milieu isotrope si ses propriétés physiques sont les mêmes dans des directions différentes.