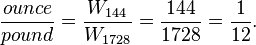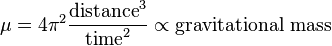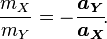Masse

Dans la physique , la masse (de grec μᾶζα «gâteau d'orge, forfaitaire (de pâte)») se réfère à la quantité de matière dans un objet. Plus précisément, la masse inertielle est une mesure quantitative de la résistance d'un objet à l'accélération . En plus de cela, la masse gravitationnelle est une mesure quantitative qui est proportionnelle à l'amplitude de la la force de gravité qui est

1. exercée par un objet (de masse gravitationnelle actif), ou
2. vécue par un objet (force gravitationnelle passive)

lors de l'interaction avec un second objet. Le Unité de mesure de masse est le kilogramme (kg).

En utilisation quotidienne, la masse est parfois appelée " poids ", dont les parts peuvent être livres ou en kilogrammes (par exemple, le poids d'une personne peut être déclaré comme 75 kg). Lors de l'utilisation scientifique, cependant, le terme« poids »se réfère à un différent, mais connexe, propriété de la matière. Le poids est la force gravitationnelle agissant sur un corps-qui, étant donné diffère selon l'attraction gravitationnelle du corps adverse (par exemple, le poids d'une personne sur la Terre vs sur la Lune ) - tandis que la masse est une propriété intrinsèque de ce corps qui ne change jamais. En d'autres termes, le poids d'un objet dépend de son environnement, tandis que sa masse ne est pas. Sur la surface de la Terre, un objet d'une masse de 50 kg pèse 491 newtons; sur la surface de la Lune, le même objet a encore une masse de 50 kg, mais ne pèse que 81,5 newtons. Retraité en termes mathématiques, sur la surface de la Terre, le poids W d'un objet est lié à sa masse m par W = m g, où g = 9,806 6 5 m / s ² est la Le champ gravitationnel de la Terre, (exprimée en accélération subie par un objet en chute libre).

La masse d'inertie d'un objet détermine son accélération en présence d'une force appliquée. Selon la deuxième loi de Newton sur le mouvement , si un corps de masse m fixe est soumis à une force unique F, son accélération est donnée par un ^F / _m. A la masse de corps détermine également le degré auquel il génère ou est affecté par une champ gravitationnel. Si un premier corps de masse m _A est placé à une distance r (de centre de masse et le centre de masse) d'un deuxième corps de masse m _B, chaque corps subit une jolie force F _g = Gm _A m _B / r ^2, où G = 6,67 × 10 ^-11 kg N ^-2 m ² est le «universel .. constante gravitationnelle "Ce est parfois appelée masse gravitationnelle expériences répétées depuis le 17ème siècle ont démontré que la masse inertielle et gravitationnelle sont équivalentes; depuis 1915, cette observation a été entraîné a priori dans le principe d'équivalence de la relativité générale .

Relativité restreinte montre que masse au repos (ou masse invariante) et l'énergie de repos sont essentiellement équivalents, par l'intermédiaire de la relation bien connue E = mc ^2. Cette même équation se connecte également masse relativiste et «l'énergie relativiste" (de l'énergie totale du système). Ces deux derniers masse et l'énergie "relativiste" sont des concepts qui sont liés à leurs homologues «repos», mais ils ne ont pas la même valeur que leurs homologues de repos dans les systèmes où il ya une impulsion nette. Afin de déduire l'une de ces quatre quantités de l'un des autres, dans ne importe quel système qui a une impulsion nette, une équation qui prend en compte l'élan est nécessaire. Mass (tant que le type et la définition de la masse est convenu) est une quantité conservée au fil du temps. Du point de vue de tout observateur non accéléré seule, la masse ne peut être ni créée ni détruite, et la relativité restreinte ne change pas cette compréhension. Tous les observateurs non accéléré accord sur le montant des masse invariante dans des systèmes fermés en tout temps, et bien que différents observateurs peuvent ne pas être d'accord avec l'autre sur combien masse relativiste est présent dans un tel système, tous conviennent que le montant ne change pas au fil du temps.

Macroscopiquement, la masse est associé à la matière importe -bien, contrairement à la masse, est mal défini dans la science. Sur l'échelle sub-atomique, non seulement fermions, les particules souvent associées avec la matière, mais aussi certains bosons, les particules qui agissent comme transporteurs vigueur, ont masse au repos. Un autre problème pour la définition facile est qu'une grande partie de la masse au repos de la matière ordinaire dérive de la masse invariante contribué à la matière par les particules et les énergies cinétiques qui ne ont pas de masse au repos eux-mêmes (seulement 1% de la masse reste de la matière se explique par le reste masse de ses quarks fermioniques et électrons). Du point de vue de la physique fondamentale, la masse est le nombre décrivant dans lesquelles le représentation de la petit groupe de la Groupe de Poincaré transforme une particule. Dans le modèle standard de la physique des particules, cette symétrie est décrit comme découlant d'une conséquence d'un couplage des particules avec masse au repos à un plus postulée domaine, connu sous le nom Champ de Higgs.

La masse totale de l' univers observable est estimé à entre 10 et ⁵² kg ⁵³ kg 10, correspondant à la masse au repos comprise entre 10 ⁷⁹ et 10 ⁸⁰ protons .

Unités de masse

Le kilogramme est l'un des sept unités de base du SI ; parmi ceux-ci, il est l'un des trois, y compris la seconde et le kelvin , qui sont définies ad hoc, sans référence à une autre unité de base. Depuis 1889, le kilogramme a été défini au moyen du prototype international kg .

échelles de la balance permettent de comparer directement la masse gravitationnelle dans un champ gravitationnel. Ces dispositifs ont été en usage depuis au moins le Moyen Âge du Bronze (montré est un équilibre pour peser le tabac datant du milieu du 19e siècle).

Dans le Système international d'unités (SI), la masse est mesurée en kilogrammes (kg). Le gramme (g) est _^1/1000 d'un kilogramme. Le programme a d'abord été introduit en 1795, avec une définition basée sur la densité de l'eau (de sorte qu'à la température de fusion de la glace , un centimètre cube d'eau aurait une masse d'un gramme, tandis que le compteur au moment été définie comme la 10000000ème partie de la distance de l' équateur de la Terre à la Pôle Nord). Depuis 1889, le kilogramme a été défini comme la masse du prototype international kg , et en tant que tel est indépendant du compteur, ou les propriétés de l'eau. En Octobre 2011, le 24 Conférence générale des poids et mesures résolues à «prendre note de l'intention" de redéfinir le kilogramme en termes de La constante de Planck, prévue pour 2014.

D'autres unités sont acceptées pour une utilisation dans SI:

• Le tonne (t) est égale à 1000 kg.
• Le électronvolt (eV) est principalement une unité de l'énergie , mais à cause de la l'équivalence masse-énergie, il peut également fonctionner comme une unité de masse. Dans ce contexte, il est noté eV / c ^2, ou tout simplement comme eV. L'électronvolt est commun dans la physique des particules .
• Le unité de masse atomique (u) est définie de sorte qu'un seul atome de carbone-12 a une masse de 12 u; U 1 est d'environ 1,66 × 10 ^-27 kg. L'unité de masse atomique est pratique pour exprimer les masses des atomes et des molécules.

En dehors du système SI, une variété de différentes unités de masse sont utilisés, selon le contexte, comme la slug (sl), le livre (lb), le Masse de Planck (m _P), et de la masse solaire.

En situation normale, le poids d'un objet est proportionnelle à sa masse, ce qui fait qu'il est souvent pose pas de problème à utiliser la même unité pour les deux concepts. Cependant, la distinction entre la masse et le poids devient important pour les mesures avec une précision meilleure que quelques pour cent (en raison de légères différences dans l'intensité de la Champ gravitationnel à différents endroits de la Terre), et pour les lieux éloignés de la surface de la Terre, tels que dans l'espace ou sur d'autres planètes.

Une masse peut parfois être exprimée en termes de longueur. La masse d'une très petite particule peut être identifié avec son inverse Compton longueur d'onde (cm ^-1 1 ≈ 3,52 x 10 ^-41 kg). La masse d'une très grande étoile ou trou noir peut être identifié avec son Rayon de Schwarzschild (1 cm ≈ 6,73 × 10 ²⁴ kg).

Résumé des concepts et formalismes de masse

Dans la mécanique classique , la masse a un rôle central dans la détermination du comportement des corps. seconde loi de Newton concerne la vigueur F exercée dans un corps de masse m du corps accélération de un:

.

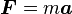En outre, la masse d'un corps concerne dynamique p à son linéaire vitesse v:

,

et le corps de l'énergie cinétique K à sa vitesse:

.

Dans la relativité restreinte , masse relativiste est un formalisme qui tient compte des effets relativistes en ayant l'augmentation de la masse avec la vitesse.

Puisque l'énergie dépend de la trame de référence (à l'observateur), il est commode de formuler les équations de la physique de telle sorte que les valeurs de masse sont invariantes (ne pas changer) entre les observateurs, et de sorte que les équations sont indépendants l'un de l'observateur. Pour une seule particule, cette quantité est la masse au repos; pour un système de particules reliées ou non, cette quantité est la masse invariante. La masse invariante M d'un corps est lié à son énergie E et l'ampleur de son élan par p

où c est la vitesse de la lumière .

Résumé des concepts liés à la masse

La relation entre les propriétés de la masse et de leurs constantes physiques associés. Chaque objet massif est censé présenter tous les cinq propriétés. Toutefois, en raison de très grandes ou très petites constantes, il est généralement impossible de vérifier plus de deux ou trois propriétés pour ne importe quel objet.

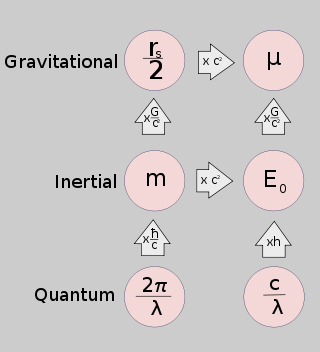
• Le Rayon de Schwarzschild (r _s) représente la capacité de la masse pour provoquer une courbure dans l'espace et le temps.
• Le gravitationnelle paramètre standard (μ) représente la capacité d'un corps massif pour exercer des forces de gravitation de Newton sur d'autres organes.
• Masse inertielle (m) représente la réponse newtonienne de la masse des forces.
• Énergie au repos (E ₀₎ représente la capacité de la masse pour être converti en d'autres formes d'énergie.
• Le Compton longueur d'onde (λ) représente la réponse quantique de la masse à la géométrie locale.

En sciences physiques , on peut distinguer conceptuellement entre au moins sept aspects différents de la masse, ou sept notions physiques qui impliquent le concept de masse:

• La quantité de la matière dans certains types d'échantillons peut être exactement déterminée par électrodéposition ou d'autres processus précis . La masse d'un échantillon exact est déterminé en partie par le nombre et le type d'atomes ou de molécules qu'il contient, et en partie par l'énergie impliquée dans la liaison ensemble (ce qui contribue un négatif "masse manquante", ou le déficit de masse).

• Masse inertielle est une mesure de la résistance d'un objet à l'évolution de son état de mouvement lorsqu'un vigueur est appliquée. Elle est déterminée en appliquant une force à un objet et de mesure de l'accélération résultant de cette force. Un objet avec une petite masse inertielle permettra d'accélérer plus qu'un objet avec une grande masse d'inertie sous l'action de la même force. On dit le corps de plus grande masse a une plus grande inertie.

• Masse gravitationnelle active (* voir ci-dessous) est une mesure de la force d'un objet de gravitationnelle flux (flux gravitationnel est égale à l'intégrale de surface du champ de gravité sur une surface de délimitation). Champ gravitationnel peut être mesurée en permettant un petit 'objet de test »pour tomber librement et en mesurant sa accélération en chute libre. Par exemple, un objet en chute libre près de la Lune va éprouver moins de champ gravitationnel, et donc accélérer plus lent que le même objet serait si elle était en chute libre près de la Terre. Le champ gravitationnel près de la Lune est plus faible parce que la Lune a une masse gravitationnelle moins actif.

• Masse gravitationnelle Passif (* voir ci-dessous) est une mesure de la force de l'interaction de l'objet avec une champ gravitationnel. Masse gravitationnelle passif est déterminée en divisant le poids d'un objet par son accélération en chute libre. Deux objets dans le même champ gravitationnel connaîtront la même accélération; Toutefois, l'objet avec une masse gravitationnelle petit passive connaîtra une force plus petite (moins de poids) que l'objet d'une plus grande masse gravitationnelle passive.

• L'énergie a également massique selon le principe de équivalence masse-énergie. Cette équivalence est illustré dans un grand nombre de processus physiques, y compris la production de paires, fusion nucléaire, et la gravitation flexion de la lumière. la production de paires et la fusion nucléaire sont des processus à travers lequel des quantités mesurables de masse et l'énergie sont converties dans l'autre. Dans la courbure gravitationnelle de la lumière, les photons d'énergie pure sont présentés à présenter un comportement similaire à la masse gravitationnelle passive.

• Courbure de l'espace-temps est une manifestation relativiste de l'existence de la masse. Courbure est extrêmement faible et difficile à mesurer. Pour cette raison, la courbure n'a pas été découvert jusqu'à ce qu'il a été prédit par la théorie d'Einstein de la relativité générale. Extrêmement précise horloges atomiques à la surface de la terre, par exemple, se trouvent à mesurer moins de temps (plus lent) que les horloges semblables dans l'espace. Cette différence de temps écoulé est une forme de courbure appelée gravitationnelle dilatation du temps. D'autres formes de courbure ont été mesurés à l'aide du Gravity Probe B par satellite.

• Quantum masse se manifeste comme une différence entre le montant d'un objet sa fréquence et nombre d'onde. La masse quantique d'un électron, le Compton longueur d'onde, peut être déterminé par diverses formes de spectroscopie et est étroitement liée à la Constante de Rydberg, le Rayon de Bohr, et la Électron. La masse quantique des objets plus grands peut être directement mesurée en utilisant un équilibre watts. En mécanique quantique relativiste, la masse est l'une des étiquettes de représentation irréductibles du groupe de Poincaré.

* NOTE: La distinction entre "actif" et "passif" masse gravitationnelle ne existe pas dans la vue de gravité newtonienne que l'on trouve dans la mécanique classique , et peut être ignoré par les laïcs. (Dans la plupart des applications pratiques, la gravitation newtonienne est utilisé parce qu'il est généralement suffisamment précise, et est plus simple que la relativité générale, par exemple, la NASA utilise la gravité principalement newtonienne de concevoir des missions spatiales, bien que "des précisions sont régulièrement améliorés en tenant compte de minuscules effets relativistes" .) La distinction entre "actif" et "passif" est très abstrait, et se applique à des applications de niveau post-universitaire de la Relativité Générale à certains problèmes dans la cosmologie, et est par ailleurs pas utilisé. Il ya, néanmoins, une distinction conceptuelle importante en physique newtonienne entre "masse d'inertie" et "masse gravitationnelle", bien que ces quantités sont identiques; la distinction conceptuelle entre ces deux définitions fondamentales de la masse est maintenu à des fins d'enseignement car ils impliquent deux méthodes distinctes de mesure. Il a été longtemps considéré comme anormal que les deux mesures distinctes de masse (inertiels et gravitationnels) ont donné le résultat identique. La propriété observé, noté par Galileo, selon laquelle des objets de différentes chute de masse avec le même taux d'accélération (en ignorant la résistance de l'air), est une expression du fait que la masse inertielle et gravitationnelle sont identiques.

Pour résumer, chaque expérience à ce jour a montré les sept valeurs ci-dessus pour être proportionnel, et dans certains cas d'égalité, cette proportionnalité et donne lieu à la notion abstraite de masse. Si, dans certains future expérience, l'un des phénomènes liés à la masse se avère pas proportionnelle aux autres, alors ce phénomène spécifique ne sera plus considérée comme une partie de la notion abstraite de la masse.

Poids et le montant

Représentation de début des balances dans le Papyrus de Hounéfer (daté du 19ème dynastie, ca. 1285 BC). Les spectacles de scène Anubis pesée du coeur de Hounéfer.

Poids, par définition, est une mesure de la force qui doit être appliquée pour soutenir un objet (ie, maintenez-le au repos) dans un champ gravitationnel. Le champ gravitationnel de la Terre provoque des éléments proches de la Terre ont un poids. Typiquement, les champs gravitationnels ne changent que marginalement sur de courtes distances, et le champ de la Terre est presque uniforme à tous les endroits sur la surface de la Terre; par conséquent, le poids d'un objet change légèrement quand il est déplacé d'un endroit à un autre, et ces petits changements est passé inaperçu pendant la majeure partie de l'histoire. Cela peut avoir donné les premiers humains l'impression que le poids est une propriété fondamentale immuable des objets dans le monde matériel. En outre, la mesure de poids en utilisant une balance ne est pas affectée par les variations de force du champ gravitationnel, et donc ce était un non-problème dans les premiers temps.

Dans l'Egyptien illustration religieuse vers la droite, Anubis utilise une balance pour peser le coeur de Hounéfer. Un échelle de balance équilibre la force du poids d'un objet contre la force du poids d'un autre objet. Les deux côtés de l'échelle de l'équilibre sont suffisamment proche pour que les objets subissent champs gravitationnels similaires. Par conséquent, se ils ont des masses similaires alors leurs poids seront également similaire. Cela permet l'échelle, par des poids comparant, à comparer également masses, et lui donne la particularité d'être une des plus anciennes dispositifs connus capables de mesurer la masse.

Le concept de montant est très vieux et antérieure à l'histoire, de sorte que toute description de l'évolution rapide de ce concept est de nature spéculative. Cependant, on peut raisonnablement supposer que les humains, à un époque début, ont compris que le poids d'une collection d'objets similaires était directement proportionnelle au nombre d'objets de la collection:

où W est le poids de la collection d'objets similaires, et n est le nombre d'objets dans la collection. La proportionnalité, par définition, implique que les deux valeurs ont une constante rapport:

, Ou de manière équivalente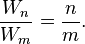

Par conséquent, les normes de poids historiques étaient souvent définis en termes de quantités. Les Romains, par exemple, utilisé le graine de caroube ( carats ou siliqua) comme étalon de mesure. Si le poids d'un objet est équivalent à 1728 graines de caroube, l'objet a été dit à peser une livre romaine. Si, d'autre part, le poids de l'objet était équivalente à 144 graines de caroube puis l'objet a été dit à peser une once romaine (uncia). Le livre romaine et onces ont tous deux été définies en termes de taille différentes collections de la même norme masse commune, la graine de caroube. Le rapport d'une once romaine (144 graines de caroube) à un livre romaine (1728 graines de caroube) était:

Cet exemple illustre un phénomène fréquent dans la science physique: lorsque les valeurs sont liées par des fractions simples, il ya une bonne possibilité que les valeurs proviennent d'une source commune.

Divers atomes et des molécules comme illustré dans John Dalton un nouveau système d 'de la philosophie chimique (1808)

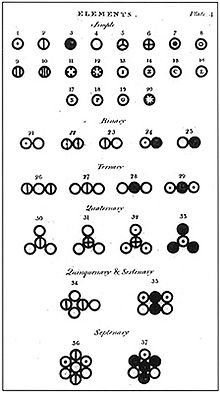
Le nom atome vient du grec ἄτομος / átomos, α-τέμνω, ce qui signifie insécable, quelque chose qui ne peut être divisé plus loin. Le concept philosophique qui pourrait être composé de matière unités discrètes qui ne peuvent être divisées a été autour depuis millénaires. Toutefois, la preuve empirique et l'acceptation universelle de l'existence des atomes ne se produisent pas jusqu'à ce que le début du 20e siècle.

Comme la science de la chimie mûri, preuve expérimentale de l'existence des atomes est venu de la loi des proportions multiples. Lorsque deux ou plusieurs éléments combinés pour former un composé, leurs masses sont toujours dans un rapport fixe et déterminé. Par exemple, le rapport massique de l'azote à l'oxygène dans l'oxyde nitrique est sept huit. L'ammoniac a un hydrogène à l'azote rapport massique de trois quatorzièmes. Le fait que les masses élémentaires combinés dans des fractions simples suggère que tous masse élémentaire provient d'une source commune. En principe, la situation de la masse atomique est analogue à l'exemple ci-dessus des unités de masse romains. Le livre romaine et onces ont tous deux été définies en termes de taille différentes collections de graines de caroube, et par conséquent, les deux unités de masse ont été liés les uns aux autres par une fraction simple. Comparativement, puisque toutes les masses atomiques sont liés entre eux par des fractions simples, alors peut-être les masses atomiques sont juste différentes collections de taille de certains unité fondamentale commune de masse.

En 1805, le chimiste John Dalton a publié sa première table de poids atomiques relatives, énumérant six éléments, hydrogène , oxygène , azote , carbone , soufre et phosphore , et l'attribution de l'hydrogène une masse atomique de 1. Et en 1815, le chimiste William Prout a conclu que l'atome d'hydrogène est en fait l'unité de masse fondamentale à partir de laquelle toutes les autres masses atomiques ont été dérivées.

Les atomes de carbone dans le graphite (image obtenue avec un tunnel à balayage de microscope)

Si L'hypothèse de Prout avait avérées exactes, alors le concept abstrait de la masse, comme nous le savons maintenant il, ne auraient jamais évolué, depuis la masse pourrait toujours être défini en termes de montants de la masse atomique de l'hydrogène. L'hypothèse de Prout; cependant, se est avéré être inexacts dans deux grands égards. Premièrement, de nouvelles avancées scientifiques ont révélé l'existence de particules plus petites, telles que des électrons et quarks , dont les masses ne sont pas liés par des fractions simples. Et en second lieu, les masses élémentaires se sont révélées ne pas être un multiple exact de l'atome d'hydrogène de masse, mais plutôt, ils étaient près multiples. La théorie de la relativité d'Einstein a expliqué que lorsque les protons et les neutrons sont réunis pour former un noyau atomique , une partie de la masse du noyau est libérée sous forme de énergie de liaison. Le plus étroitement lié le noyau, plus l'énergie est perdue lors de la formation et de cette perte d'énergie de liaison provoque les masses élémentaires à ne pas être liés par des fractions simples.

Un atome d'hydrogène, par exemple, avec un proton, a un poids atomique d'1.007825 u. Le plus abondant isotope de fer a 26 protons et 30 neutrons, donc on pourrait se attendre à son poids atomique d'être 56 fois supérieur à celui de l'atome d'hydrogène, mais en fait, son poids atomique est seulement 55,9383 u, ce qui ne est clairement pas un nombre entier multiple de 1,007825. L'hypothèse de Prout a été prouvé inexactes à bien des égards, mais les concepts abstraits de masse atomique et le montant de continuer à jouer un rôle influent dans la chimie, et la unité de masse atomique continue d'être l'unité de choix pour de très petites mesures de masse.

Messes pour une utilisation avec des balances

Quand les Français a inventé le système métrique à la fin du 18ème siècle, ils ont utilisé un montant à définir leur unité de masse. La kg a été initialement défini comme étant égal à la masse de la quantité de l'eau pure contenue dans un récipient d'un litre. Cette définition, cependant, était insuffisant pour les exigences de précision de la technologie moderne, et le kilogramme métrique a été redéfinie en termes de un bar platine-iridium artificiel connu sous le nom kg internationale de prototype.

La masse gravitationnelle

Masse gravitationnelle actif est une propriété de la masse d'un objet qui produit un champ gravitationnel dans l'espace entourant l'objet, et ces champs gravitationnels régissent les structures à grande échelle dans l' Univers . Champs gravitationnels détiennent les galaxies ensemble. Ils provoquent des nuages de gaz et poussière se concentre en étoiles et planètes . Ils fournissent la pression nécessaire pour la fusion nucléaire de se produire dans les étoiles. Et ils déterminent la orbites de divers objets dans le système solaire . Depuis effets gravitationnels sont tout autour de nous, il est impossible de cerner la date exacte à laquelle les humains d'abord découvert la masse gravitationnelle. Cependant, il est possible d'identifier certaines des étapes importantes vers notre compréhension moderne de la masse gravitationnelle et sa relation avec les autres phénomènes de masse. Certains termes associés à la masse gravitationnelle et ses effets sont les Gaussienne constante gravitationnelle, la paramètre gravitationnelle standard et le Rayon de Schwarzschild.

Masse gravitationnelle de Kepler

Johannes Kepler 1610

Anglais nom		Les planètes de Kepler
		Demi-grand axe	Période orbitale sidéral	Messe de Sun
Mercure		0,387 099 UA	0,240 842 année sidérale
Vénus		0,723 332 UA	0,615 187 année sidérale
Terre		1,000 000 UA	1,000 000 année sidérale
Mars		1,523 662 UA	1,880 816 année sidérale
Jupiter		5,203 363 UA	11,861 776 année sidérale
Saturne		9,537 070 UA	29,456 626 année sidérale

Johannes Kepler était le premier à donner une description précise des orbites des planètes, et, ce faisant; il fut le premier à décrire la masse gravitationnelle. En 1600, Kepler a cherché un emploi avec Tycho Brahe et par conséquent a eu accès à des données astronomiques d'une précision supérieure à ceux qui sont déjà disponibles. En utilisant des observations précises de Brahe de la planète Mars, Kepler est rendu compte que les méthodes traditionnelles astronomiques étaient inexactes dans leurs prédictions, et il a passé les cinq prochaines années à développer sa propre méthode pour caractériser le mouvement des planètes.

En définitive modèle planétaire de Kepler, il a décrit avec succès orbites planétaires comme suivant elliptiques chemins avec le Soleil en un point focal de l'ellipse. Le concept de masse gravitationnelle actif est une conséquence immédiate de Kepler de la troisième loi du mouvement planétaire . Kepler a découvert que le carré de la période orbitale de chaque planète est directement proportionnelle à la cube de la demi-grand axe de son orbite, ou de manière équivalente, que le rapport de ces deux valeurs est constante pour toutes les planètes dans le système solaire . Ce rapport constant est une mesure directe de la masse gravitationnelle active du Soleil, elle a unités de distance cubes par temps au carré, et est connu comme le Paramètre gravitationnel standard:

Anglais nom		Les lunes galiléennes
		Demi-grand axe	Période orbitale sidéral	Masse de Jupiter
Io		0,002 819 UA	0,004 843 année sidérale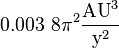
Europa		0,004 486 UA	0,009 722 année sidérale
Ganymède		0,007 155 UA	0,019 589 année sidérale
Callisto		0,012 585 UA	0,045 694 année sidérale

En 1609, Johannes Kepler a publié ses trois règles connus comme Lois de Kepler, en expliquant comment les planètes suivent des orbites elliptiques sous l'influence du Soleil Le 25 Août de la même année, Galileo Galilei de démontrer son premier télescope à un groupe de marchands vénitiens, et au début de Janvier de 1610, Galileo a observé quatre objets faibles près de Jupiter, qu'il prenait pour étoiles. Cependant, après quelques jours d'observation, Galileo est rendu compte que ces «étoiles» étaient en fait en orbite autour de Jupiter. Ces quatre objets (nommés plus tard, le Lunes galiléennes en l'honneur de leur découvreur) ont été les premiers corps célestes observés en orbite quelque chose d'autre que la Terre et du Soleil Galileo a continué à observer ces lunes au cours des dix-huit prochains mois, et par le milieu de 1611, il avait obtenu des estimations remarquablement précises pour leurs périodes. Plus tard, le demi-grand axe de chaque moon a également estimé, permettant ainsi la masse gravitationnelle de Jupiter pour être déterminé à partir des orbites de ses lunes. La masse gravitationnelle de Jupiter a été trouvé à environ un millième de la masse gravitationnelle du Soleil

Champ gravitationnel galiléen

Galileo Galilei 1636

Distance parcourue par une balle en chute libre est proportionnelle au carré du temps écoulé

Quelque temps avant 1638, Galileo a tourné son attention sur le phénomène de chute d'objets sous l'influence de la gravité terrestre, et il a été activement tente de caractériser ces motions. Galileo ne était pas le premier à enquêter sur le champ gravitationnel de la Terre, il ne était pas le premier à décrire avec précision ses caractéristiques fondamentales. Toutefois, la dépendance de Galileo sur l'expérimentation scientifique pour établir des principes physiques aurait un effet profond sur les futures générations de scientifiques. Galileo a utilisé un certain nombre d'expériences scientifiques pour caractériser le mouvement de chute libre. On ne sait pas se il se agissait simplement expériences hypothétiques utilisés pour illustrer un concept, ou se ils étaient de véritables expériences réalisées par Galileo, mais les résultats obtenus à partir de ces expériences étaient à la fois réaliste et convaincante. Une biographie par l'élève de Galileo Vincenzo Viviani a déclaré que Galilée avait chuté boules de la même matière, mais des masses différentes, de la Tour de Pise pour démontrer que leur temps de descente était indépendante de leur masse. À l'appui de cette conclusion, Galileo avait avancé l'argument théorique suivante: Il m'a demandé si deux corps de masses différentes et différents taux de chute sont liés par une chaîne, le système combiné ne tombe plus vite parce qu'il est maintenant plus massive, ou fait le briquet corps dans sa chute lente retenir le corps plus lourd? La seule solution convaincante à cette question est que tous les organismes doivent se situer au même rythme.

Une expérience plus tard, a été décrit dans deux nouvelles sciences de Galileo publiés en 1638. Un des personnages fictifs de Galilée, Salviati, décrit une expérience utilisant une boule de bronze et une rampe en bois. La rampe en bois était "12 coudées de long, une demi-coudée de large et trois de doigt d'épaisseur" avec une ligne droite, lisse et polie rainure. La gorge était bordée de " parchemin, aussi lisse et polie que possible ". Et dans cette gorge a été placé« un dur, lisse et très rond bronze balle ". La rampe a été incliné à différents angles pour ralentir l'accélération assez pour que le temps écoulé peut être mesurée. Le . balle a été autorisé à rouler sur une distance connue bas de la rampe, et le temps pris pour la balle de se déplacer de la distance connue a été mesurée Le temps a été mesurée en utilisant une horloge à eau décrite comme suit:

"Un grand récipient d'eau placé dans une position élevée; au fond de ce navire a été soudé un tuyau de petit diamètre donnant une mince jet d'eau, qui nous avons recueilli dans un petit verre pendant le temps de chaque descente, que ce soit pour l'ensemble longueur du canal ou pour une partie de sa longueur, l'eau ainsi recueillie a été pesé, après chaque descente, sur un équilibre très précis; les différences et les rapports de ces poids nous ont donné les différences et les rapports de l'époque, et cela avec une telle précision que, bien que l'opération a été répétée de nombreuses fois, il n'y avait aucune différence appréciable dans les résultats ".

Galileo a constaté que pour un objet en chute libre, la distance que l'objet est tombé est toujours proportionnelle au carré du temps écoulé:

Galileo Galilei est mort à Arcetri, Italie (près de Florence), le 8 Janvier 1642. Galileo avait montré que les objets en chute libre sous l'influence du champ gravitationnel de la Terre ont une accélération constante, et contemporain, Johannes Kepler de Galilée, avait montré que les planètes suivre des trajectoires elliptiques sous l'influence de la masse gravitationnelle du Soleil. Cependant, la relation entre le champ gravitationnel de Galileo et masse gravitationnelle de Kepler ne était pas compris pendant la vie de Galilée.

Masse gravitationnelle de Newton

Isaac Newton 1689

Lune		Masse de la Terre
Demi-grand axe	Période orbitale sidéral
0,002 569 UA	0,074 802 année sidérale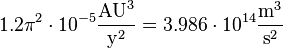
La gravité de la Terre	Rayon de la Terre
65 9,806 m / s 2	6 375 km

Robert Hooke a publié son concept de forces gravitationnelles en 1674, déclarant que, tous les organes Cœlestial que ce soit, ont une attraction ou le pouvoir gravitant vers leurs propres centres [et] ils ne attirent également tous les autres organes Cœlestial qui sont dans la sphère de leur activité . Il affirme en outre que l'attraction gravitationnelle augmente de combien le plus près du corps forgé sur est de leur propre centre. Dans une correspondance de 1679-1680 entre Robert Hooke et Newton , Hooke conjecture que les forces gravitationnelles pourraient baisser, selon le double de la distance entre les deux organes. Hooke a exhorté Newton, qui a été un pionnier dans le développement de calcul , de travailler à travers les détails mathématiques de orbites de Kepler pour déterminer si l'hypothèse de Hooke était correcte. Propres enquêtes de Newton vérifié que Hooke était correcte, mais en raison de différences personnelles entre les deux hommes, Newton choisi de ne pas révéler ce à Hooke. Isaac Newton a gardé le silence sur ses découvertes jusqu'à 1684, date à laquelle il dit à un ami, Edmond Halley , qu'il avait résolu le problème des orbites gravitationnelles, mais avait égaré la solution dans son bureau. Après avoir été encouragé par Halley, Newton a décidé de développer ses idées sur la gravité et de publier l'ensemble de ses conclusions. En Novembre 1684, Isaac Newton a envoyé un document à Edmund Halley, désormais perdu, mais présumé avoir été intitulé De motu corporum dans gyrum (latin pour "Sur le mouvement des corps dans une orbite"). Halley a présenté les conclusions de Newton à la Royal Society de Londres, avec une promesse qu'une présentation plus complète suivrait. Newton a enregistré plus tard ses idées dans un ensemble de trois livres, intitulé Philosophiae Naturalis Principia Mathematica (latin: «Principes mathématiques de la philosophie naturelle"). Le premier a été reçu par la Royal Society le 28 Avril 1685 à 6, la seconde le 2 Mars 1686 au 7, et le troisième le 6 Avril 1686-7. La Royal Society a publié toute la collection de Newton à leurs propres frais mai 1686-7.

Isaac Newton avait comblé l'écart entre la masse gravitationnelle de Kepler et de Galilée accélération gravitationnelle, et prouvé la relation suivante:

oùgest l'accélération apparente d'un corps qui passe dans une région de l'espace où les champs gravitationnels existent,μest la masse gravitationnelle (paramètre gravitationnel standard) du corps causant champs gravitationnels, etRest la coordonnée radiale (la distance entre le centres des deux organes).

En trouvant la relation exacte entre la masse gravitationnelle d'un corps et son champ gravitationnel, Newton a fourni une seconde méthode pour mesurer la masse gravitationnelle. La masse de la Terre peut être déterminée en utilisant la méthode de Kepler (à partir de l'orbite de la Lune), ou elle peut être déterminée par mesure de l'accélération gravitationnelle sur la surface de la Terre, et en multipliant ce par le carré du rayon de la Terre. La masse de la Terre est d'environ trois millionièmes de la masse du Soleil À ce jour, aucune autre méthode précise pour mesurer la masse gravitationnelle a été découvert.

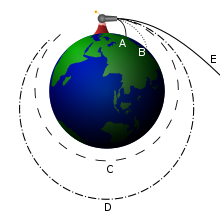
Le boulet de canon de Newton

Canon de Newton était un pensé expérience utilisé pour combler le fossé entre l'accélération gravitationnelle de Galileo et des orbites elliptiques de Kepler. Il est apparu en 1728 le livre de Newton Traité du système du monde . Selon le concept de Galileo de la gravitation, une pierre chuté tombe avec une accélération constante descendant vers la Terre. Cependant, Newton explique que quand on jette une pierre horizontalement (ce qui signifie le côté ou perpendiculaire à la gravité terrestre), il suit une trajectoire courbe. "Pour une pierre projetée est par la pression de son propre poids forcée hors de la trajectoire rectiligne, qui, par la projection seul, il aurait poursuivi et fait de décrire une ligne courbe dans l'air; et par le biais de cette façon tordue est enfin ramené au sol. Et plus la vitesse est avec laquelle il est prévu, plus elle va avant qu'il ne tombe à la Terre ".

Newton autres raisons que si un objet a été "projeté dans une direction horizontale depuis le sommet d'une haute montagne» avec une vitesse suffisante, "il serait tout à fait atteindre à la fin delà de la circonférence de la Terre, et de retour à la montagne à partir de laquelle il a été projeté . "L'expérience de pensée de Newton est illustré dans l'image vers la droite. Un canon au sommet d'une montagne très élevée tire un boulet de canon dans une direction horizontale. Si la vitesse est faible, il tombe tout simplement de retour sur Terre (chemins A et B). Cependant, si la vitesse est égale ou supérieure à un certain seuil ( de la vitesse orbitale), mais pas suffisamment élevée pour laisser Terre complètement ( vitesse de libération, chemin E), il continuera tournant autour de la terre le long d'une orbite elliptique (C et D).

Masse gravitationnelle universelle et la quantité

Le boulet de canon de Newton illustre la relation entre la masse gravitationnelle de la Terre et son champ gravitationnel; cependant, un certain nombre d'autres ambiguïtés restait encore. Robert Hooke avait affirmé en 1674 que: "Tous les corps célestes que ce soit, ont une attraction ou le pouvoir gravitant vers leurs propres centres", mais Hooke eu ni expliqué pourquoi cette attraction gravitant était unique de corps célestes, ni eu il a expliqué pourquoi l'attraction a été réalisé vers le centre d'un corps céleste.

Selon la théorie de Newton de la gravitation universelle, chaque graine de caroube produit champs gravitationnels. Par conséquent, si l'on devait rassembler un nombre immense de graines de caroube et de les former en une sphère énorme, alors le champ gravitationnel de la sphère serait proportionnelle au nombre de graines de caroube dans le domaine. Par conséquent, il devrait être théoriquement possible de déterminer le nombre exact de graines de caroube qui seraient nécessaires pour produire un champ gravitationnel similaire à celle de la Terre ou Soleil Et puisque les unités de poids romains ont tous été définis en termes de graines de caroube, alors la connaissance de la Terre, ou "la masse de graine de caroube" de Sun permettrait de calculer la masse en livres romains, ou en onces romains, ou toute autre unité romaine.

Vertical dessin de la section de torsion l'instrument de la balance de Cavendish y compris le bâtiment dans lequel il a été logé. Les grandes boules ont été suspendus à un cadre afin qu'ils puissent être tournés en position à côté des petites boules par une poulie de l'extérieur. Figure 1 du document de Cavendish.

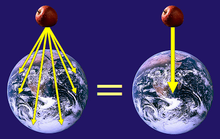
Cette possibilité va au-delà unités romaines et de la graine de caroube. La livre avoirdupois britannique, par exemple, a été défini à l'origine pour être égale à 7,000 grains d'orge. Par conséquent, si l'on pouvait déterminer "la masse de grain d'orge" de la Terre (le nombre de grains d'orge nécessaires pour produire un champ gravitationnel similaire à celle de la Terre), alors cela permettrait de calculer la masse de la Terre en livres avoirdupois. En outre, le kilogramme d'origine a été défini comme étant égal à la masse à un litre d'eau pure (le kg moderne est définie par l'artificiel kg de prototype international). Ainsi, la masse de la Terre en kilogrammes pourrait théoriquement être déterminée par déterminer combien de litres d'eau pure (ou kilogrammes prototypes internationaux) seraient nécessaires pour produire des champs gravitationnels similaires à celles de la Terre. En fait, il est une simple question de l'abstraction à réaliser que toute unité de masse traditionnels peut théoriquement être utilisé pour mesurer la masse gravitationnelle.

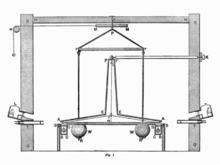
Mesurer la masse gravitationnelle en termes d'unités de masse traditionnels est simple dans son principe, mais extrêmement difficile dans la pratique. Selon la théorie de Newton tous les objets produisent des champs gravitationnels et il est théoriquement possible de recueillir un nombre immense de petits objets et de les former en une énorme sphère de gravitation. Cependant, d'un point de vue pratique, les champs gravitationnels de petits objets sont extrêmement faibles et difficiles à mesurer. Et si l'on devait recueillir un nombre immense d'objets, la sphère résultant serait probablement trop grand pour construire sur la surface de la Terre, et trop coûteux à construire dans l'espace. Les livres de Newton sur la gravitation universelle ont été publiés dans les années 1680, mais la première mesure de succès de la masse de la Terre en termes d'unités de masse traditionnels, l' expérience Cavendish, n'a pas eu lieu jusqu'en 1797, plus de cent ans plus tard. Cavendish a constaté que la densité de la Terre était 5.448 ± 0.033 fois supérieure à celle de l'eau. En 2009, la masse de la Terre en kilogrammes est connu seulement à environ cinq chiffres de précision, tandis que sa masse gravitationnelle est connu pour plus de neuf chiffres significatifs.

Inertielle et masse gravitationnelle

Bien que la masse d'inertie, la masse gravitationnelle passive et masse gravitationnelle actif sont conceptuellement distincts, aucune expérience n'a jamais clairement démontré aucune différence entre eux. Dans la mécanique classique , la troisième loi de Newton implique que la masse gravitationnelle active et passive doit toujours être identiques (ou au moins proportionnelle), mais la théorie classique propose aucune raison convaincante pour laquelle la masse gravitationnelle doit être égale à la masse d'inertie. Ce qu'il fait est simplement un fait empirique.

Albert Einstein a développé sa théorie de la relativité générale départ de l'hypothèse que cette correspondance entre inertie et (passive) masse gravitationnelle est pas accidentel: qu'aucune expérience ne sera jamais détecter une différence entre eux (la version faible de la principe d'équivalence). Cependant, dans la théorie qui en résulte, la gravitation est pas une force et donc pas soumis à la troisième loi de Newton, si «l'égalité des inertielle et actif masse gravitationnelle [...] demeure énigmatique que jamais ".

Masse inertielle

Masse d'inertieest la masse d'un objet mesuré par sa résistance à l'accélération.

Pour comprendre ce que la masse d'inertie d'un corps est, on commence avec la mécanique classique et Lois du mouvement de Newton . Plus tard, nous allons voir comment notre définition classique de la masse doit être modifié si l'on prend en considération la théorie de la relativité restreinte , qui est plus précis que la mécanique classique. Toutefois, les implications de la relativité restreinte ne seront pas changer le sens de la «masse» dans toute façon essentielle.

Selonla deuxième loi de Newton, nous disons que le corps a une massemsi, à tout instant, il obéit à l'équation du mouvement

où F est la résultante la force agissant sur ​​le corps et un est l' accélération du centre de masse du corps. Pour le moment, nous allons mettre de côté la question de ce que "la force agissant sur ​​le corps" signifie réellement.

Cette équation montre comment se rapporte à la masse d'inertie d'un corps. Considérons deux objets de masses différentes. Si nous appliquons une force identique à chacun, l'objet avec une plus grande masse connaîtra une accélération plus petit, et l'objet avec une plus petite masse connaîtra une plus grande accélération. Nous pourrions dire que la plus grande masse exerce une plus grande "résistance" à l'évolution de son état ​​de mouvement en réponse à la force.

Toutefois, cette notion de l'application de forces "identiques" à des objets différents qui nous ramène au fait que nous avons pas vraiment défini ce une force est. Nous ne pouvons contourner cette difficulté avec l'aide de la troisième loi de Newton , qui stipule que si un objet exerce une force sur un second objet, il connaîtra une force égale et opposée. Pour être précis, supposons que nous avons deux objets x et y, avec constants inertie des masses m _X et m _Y . On isole les deux objets à partir de toutes les autres influences physiques, de sorte que les seules forces en présence sont la force exercée sur X par Y, que l'on note F _XY , et la force exercée sur Y par X, que l'on note F _YX . La deuxième loi de Newton affirme que

où un _X et un _Y sont les accélérations de X et Y, respectivement. Supposons que ces accélérations sont non nulles, de sorte que les forces entre les deux objets sont non nuls. Cela se produit, par exemple, si les deux objets sont sur ​​le point d'entrer en collision avec l'autre. La troisième loi de Newton déclare ensuite que

et ainsi

Notez que notre exigenced'un _Xêtre non-zéro assure que la fraction est bien défini.

Ceci est, en principe, comment nous pourrions mesurer la masse d'inertie d'un objet. Nous choisissons un objet "de référence" et de définir sa masse m _Y que (par exemple) un kilogramme. Ensuite, nous pouvons mesurer la masse de tout autre objet dans l'univers par la collision avec l'objet de référence et de mesurer les accélérations.

Masse gravitationnelle de Newton

Le concept newtonien de masse gravitationnelle repose sur La loi de la gravitation de Newton. Supposons que nous avons deux objets A et B, séparés par une distance R _AB . La loi de la gravitation stipule que si A et B ont des masses gravitationnelles M _UNE et M _B , respectivement, puis chaque objet exerce une force gravitationnelle sur l'autre, de grandeur

,

oùGest l'universel constante gravitationnelle.La déclaration ci-dessus peut être reformulée de la façon suivante: sigest l'ampleur à un endroit donné dans un champ gravitationnel, alors la force gravitationnelle sur un objet avec une masse gravitationnelleMest

.

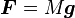Ceci est la base de masses qui sont déterminées par pesée. En simples balances à ressort, par exemple, la force F est proportionnelle au déplacement du printemps sous le plateau de pesée, selon la loi de Hooke, et les échelles sont étalonnée pour tenir g en compte, permettant la masse M à lire off. Un équilibre mesures de masse gravitationnelle; seul le ressort des mesures à l'échelle de poids.

Equivalence des masses d'inertie et gravitationnels

L'équivalence des masses d'inertie et gravitation est parfois appelé le «principe d'équivalence galiléen» ou le « principe d'équivalence faible ». La conséquence la plus importante de ce principe d'équivalence applique à des objets en chute libre. Supposons que nous ayons un objet avec inertiels et gravitationnels masses m et M , respectivement. Si la seule force agissant sur ​​l'objet vient d'un champ gravitationnel g , combinant la deuxième loi de Newton et la loi de gravitation donne l'accélération

Ceci indique que le rapport de la masse d'inertie gravitationnelle d'un objet quelconque est égale à une constante K si et seulement si tous les objets tombent à la même vitesse dans un champ gravitationnel donné. Ce phénomène est appelé le "universalité de la chute libre». (En outre, la constante K peut être considéré comme 1 en définissant nos unités de manière appropriée.)

Les premières expériences démontrant l'universalité de la chute libre ont été réalisées par Galileo . Il est communément dit que Galileo a obtenu ses résultats par la chute d'objets à partir de la tour penchée de Pise , mais cela est probablement apocryphe; en fait, il a effectué ses expériences avec des boules de roulement en baisse de près frictionaless plans inclinés pour ralentir le mouvement et d'augmenter la précision de la synchronisation. Expériences de plus en plus précises ont été réalisées, telles que celles effectuées par Loránd Eötvös, en utilisant la torsion équilibre pendule, en 1889. En 2008, aucun écart par rapport à l'universalité, et donc de l'équivalence de Galilée, n'a jamais été trouvé, au moins à la précision 10 ^-12 . efforts expérimentaux plus précis sont encore en cours.

L'universalité de la chute libre applique uniquement aux systèmes dans lesquels la gravité est la seule force agissant. Tous les autres forces, en particulier frottement et la résistance de l'air, doivent être absents ou au moins négligeable. Par exemple, si un marteau et une plume sont supprimés de la même hauteur dans l'air sur la Terre, la plume prendra beaucoup plus de temps pour atteindre le sol; la plume est pas vraiment en libre -fall parce que la force de résistance de l'air vers le haut contre la plume est comparable à la force vers le bas de la gravité. D'autre part, si l'expérience est effectuée dans un vide, dans lequel il n'y a pas de résistance de l'air, le marteau et l'angle de croisement doit frapper le sol à la même heure (en supposant que l'accélération des deux objets l'un vers l'autre, et de la sol vers les deux objets, pour sa part, est négligeable). Cela peut facilement être fait dans un laboratoire de haute école en laissant tomber les objets dans des tubes transparents qui ont l'air enlevé avec une pompe à vide. Il est encore plus dramatique lorsqu'il est effectué dans un environnement qui a naturellement un vide, comme David Scott a fait sur ​​la surface de la Lune au cours Apollo 15.

Une version plus forte du principe d'équivalence, connu comme le principe d'équivalence d'Einstein ou principe d'équivalence forte , se trouve au cœur de la théorie de la relativité générale . Le principe d'équivalence d'Einstein affirme que, dans suffisamment petites régions de l'espace-temps, il est impossible de distinguer entre une accélération uniforme et un champ gravitationnel uniforme. Ainsi, la théorie postule que la force agissant sur ​​un objet massif causé par un champ gravitationnel est le résultat de la tendance de l'objet à déplacer en ligne droite (en d'autres termes son inertie) et devrait donc être fonction de sa masse inertielle et de la la force du champ gravitationnel.

Masse et d'énergie dans la relativité spéciale

Le terme de masse en relativité restreinte se réfère généralement à la masse au repos de l'objet, qui est la masse newtonienne telle que mesurée par un observateur se déplaçant avec l'objet. Le masse invariante est un autre nom pour la masse au repos de particules simples. Cependant, plus la masse invariante générale (calculée par une formule plus complexe) peut également être appliquée à des systèmes de particules en mouvement relatif, et de ce fait, est habituellement réservée aux systèmes qui sont constitués de particules de haute énergie largement séparées. La masse invariante de systèmes est le même pour tous les observateurs et les cadres d'inertie, et ne peut pas être détruite, et est ainsi conservée, tant que le système est fermé. Dans ce cas, «fermeture» implique qu'une limite idéalisée est tracé autour du système, et pas de masse / énergie est autorisé à travers elle.

Dans la mesure où l'énergie est conservée dans des systèmes fermés de la relativité, la masse d'un système est également une quantité qui est conservée: cela signifie qu'il ne change pas au fil du temps, même si certains types de particules sont convertis en d'autres. Pour tout observateur donné, la masse de tout système est conservé séparément et ne peut pas changer au fil du temps, tout comme l'énergie est conservée séparément et ne peut pas changer au fil du temps. L'idée populaire erronée que la masse peut être converti en (sans masse) d'énergie en relativité est parce que certains matière particules peuvent dans certains cas être convertis en types d'énergie qui ne sont pas la matière (comme la lumière, l'énergie cinétique et l'énergie potentielle magnétique, électrique, et d'autres domaines). Cependant, cette confond «matière» (une chose non conservé et mal défini) de masse (qui est bien définie et est conservée). Même si pas considéré comme «matière», tous les types d'énergie continuent à présenter de masse dans la relativité. Ainsi, la masse et l'énergie ne changent pas dans l'autre dans la relativité; plutôt, les deux sont des noms pour la même chose, et ni masse ni l'énergie semble sans l'autre. Particules "matière" ne peuvent pas être conservés dans les réactions à la relativité, mais la masse-système fermé est toujours.

Par exemple, une bombe nucléaire dans une boîte de super-forte idéalisée, assis sur une échelle, serait en théorie montrer aucun changement dans la masse quand explosé (bien que l'intérieur de la boîte serait beaucoup plus chaud). Dans un tel système, la masse de la boîte allait changer que si l'énergie ont été autorisés à sortir de la boîte comme la lumière ou à la chaleur. Cependant, dans ce cas, l'énergie retirée prendrait sa masse qui lui est associée. Laisser la chaleur d'un tel système est tout simplement une façon d'enlever la masse. Ainsi, la masse, comme l'énergie, ne peut être détruit, mais seulement déplacé d'un endroit à l'autre.

Dans les systèmes liés, l' énergie de liaison doit (souvent) être soustraite de la masse du système non lié, tout simplement parce que cette énergie a une masse, et cette masse est soustrait du système quand il se dégage, au moment où il est lié. La messe est pas conservée dans ce processus parce que le système ne soit pas fermé pendant le processus de liaison. Un exemple bien connu est l'énergie de liaison des noyaux atomiques , qui apparaît comme d'autres types d'énergie (tels que les rayons gamma) lorsque les noyaux sont formés, et (après avoir été dégagée) des résultats dans des nucléides qui ont moins de masse que les particules libres ( nucléons ) dont elles sont composées.

Le terme masse relativiste est également utilisé, et cela est la quantité totale d'énergie dans un corps ou d'un système (divisé par c ² ). La masse relativiste (d'un corps ou d'un système de corps) comprend une contribution de l'énergie cinétique du corps, et est plus gros plus vite le corps se déplace, si différent de la masse invariante, la masse relativiste dépend de l'observateur de cadre de réference. Toutefois, pour donnée unique cadres de référence et pour des systèmes fermés, la masse relativiste est également une quantité conservée.

Parce que la masse relativiste est proportionnelle à l'énergie, il a peu à peu tombé en désuétude parmi les physiciens. Il ya désaccord quant à savoir si le concept reste pédagogiquement utile.

Messe en la relativité générale

Dans la relativité générale , le principe d'équivalence est un des nombreux concepts connexes portant sur ​​l'équivalence des gravitationnelle et la masse inertielle . Au cœur de cette affirmation est d'Albert Einstein l'idée que la force gravitationnelle telle qu'elle est vécue au niveau local tout en se tenant sur ​​un corps massif (comme la Terre) est le même que le pseudo-force de l'expérience par un observateur dans un non inertiel (accélérée) de référence.

Cependant, il se trouve qu'il est impossible de trouver une définition générale objective pour le concept de masse invariante en relativité générale. Au coeur du problème réside dans la non-linéarité des équations de champ d'Einstein, ce qui rend impossible d'écrire l'énergie du champ de gravitation dans le cadre du tenseur de contrainte-énergie d'une manière qui est invariante pour toutes les observateurs. Pour un observateur donné, ceci peut être réalisé par le stress pseudotensoriel-impulsion-énergie.

Messe dans la physique quantique

Dansla mécanique classique, la masse inerte d'une particule apparaît dans l'équation d'Euler-Lagrange comme un paramètrem,

.

Après quantification, en remplaçant le vecteur de positionxavec unefonction d'onde, le paramètremapparaît dans l'énergie cinétiqueopérateur,

.

Dans la ostensiblementcovariant (relativiste invariant)équation de Dirac, etunités naturelles, cela devient

Lorsque la "masse "paramètremest maintenant simplement une constante associée à l'quantique décrit par la fonction d'onde ψ.

Dans le modèle standard de la physique des particules tels que développés dans les années 1960, il est la proposition que ce terme provient de l'accouplement de l'ψ de champ à un Φ de champ supplémentaire, la soi-disant Champ de Higgs. Dans le cas des fermions, les résultats de mécanisme de Higgs dans le remplacement du terme m ψ dans le lagrangien avec 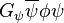. Cette décale le explanandum de la valeur pour la masse de chaque particule élémentaire à la valeur de la accouplements inconnue G _ψ . La découverte d'un massif boson de Higgs serait considérée comme une forte confirmation de cette théorie. Mais il ya des preuves indirectes de la réalité de la brisure de symétrie électrofaible tel que décrit par le mécanisme de Higgs, et de la non-existence du boson de Higgs pourrait indiquer un " Description Higgsless "de ce mécanisme.

Origine de la masse

En physique théorique, un mécanisme de masse de génération est une théorie qui tente d'expliquer l'origine de la masse des lois les plus fondamentales de la physique . À ce jour, un certain nombre de différents modèles ont été proposés qui prônent des opinions différentes à l'origine de la masse. Le problème est compliqué par le fait que la notion de masse est fortement liée à l' interaction gravitationnelle , mais une théorie de ce dernier n'a pas encore été réconcilié avec le modèle actuellement populaire de la physique des particules , connu comme le Modèle Standard .

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Mass&oldid=545481593 "