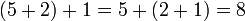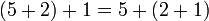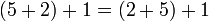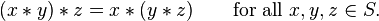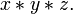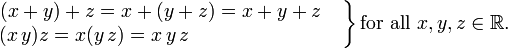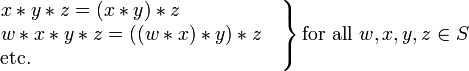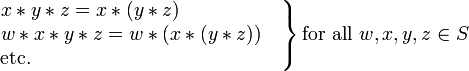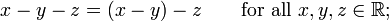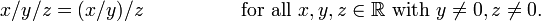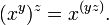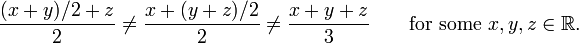Associativité

Saviez-vous ...

Cette sélection se fait pour les écoles par la charité pour enfants lire la suite . Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays

En mathématiques , l'associativité est une propriété qui a opération binaire peut avoir. Cela signifie que, dans une expression contenant deux ou plusieurs des mêmes opérateurs associatifs dans une rangée, l'ordre des opérations n'a pas d'importance tant que la séquence de la opérandes ne est pas modifiée. Autrement dit, le réarrangement parenthèses dans une telle expression ne changera pas sa valeur. Considérons par exemple l'équation

$(5 + 2) + 1 = 5 + (2 + 1) = 8$

Même si les parenthèses ont été réarrangées, la valeur de l'expression ne était pas modifiée. Comme ce est vrai lors de l'exécution plus sur les nombres réels , nous disons que "plus des nombres réels est une opération associative."

Associativité ne doit pas être confondue avec la commutativité . Commutativité justifie de modifier l'ordre ou la séquence des opérandes dans une expression tout associativité ne est pas. Par exemple,

$(5 + 2) + 1 = 5 + (2 + 1)$

est un exemple de l'associativité parce que les parenthèses ont été modifiées (et par conséquent l'ordre des opérations au cours de l'évaluation), tandis que les opérandes 5, 2 et 1 apparaissent dans le même ordre de gauche à droite dans l'expression.

$(5 + 2) + 1 = (2 + 5) 1$

ne est pas un exemple de l'associativité parce que la séquence d'opérande modifié lorsque le 2 5 et changé de place.

Opérations associatives sont abondants en mathématiques, et en fait la plupart des structures algébriques exigent explicitement leurs opérations binaires d'être associative. Cependant, de nombreuses opérations importantes et intéressantes sont non-associative; un exemple commun serait le produit vecteur de croix .

Définition

Formellement, une opération binaire $* \! \! \!$ sur un ensemble S est appelé associative se il satisfait à la loi associative:

$(X * y) z = * x * (y * z) \ qquad \ mbox {} pour tout x, y, z \ in S.$

L'ordre d'évaluation ne affecte pas la valeur de ces expressions, et il peut être démontré que la même chose pour les expressions contenant un certain nombre de $* \! \! \!$ opérations. Ainsi, lorsque $* \! \! \!$ est associative, l'ordre d'évaluation peut donc être omis sans causer ambiguïté, en omettant les parenthèses et écrire simplement:

$x * y * z. \,$

Cependant, il est important de se rappeler que changer l'ordre des opérations ne implique pas ou permettre la modification des opérations proprement dites en déplaçant les opérandes autour dans l'expression.

Exemples

Certains exemples d'opérations associatifs sont les suivantes.

En arithmétique , plus et la multiplication des nombres réels sont associative; ce est à dire,

$\ Left. \ Begin {matrix} (x + y) + z = x + (y + z) = x + y + z \ quad \\ (x \, y) z = x (y \, z) = x \, y \ , z \ qquad \ qquad \ qquad \ quad \ \ \, \ end {matrix} \ right \} \ mbox {} pour tous x, y, z \ in \ mathbb {R}.$

L'addition et la multiplication des nombres complexes et quaternions est associative. L'addition de octonions est également associatif, mais de multiplication octonions est non associatif.

Le plus grand commun diviseur et multiples fonctions moins communes agissent associative.

$\ Left. \ Begin {matrix} \ {operatorname pgcd} (\ operatorname {} pgcd (x, y), z) = \ operatorname {} pgcd (x, \ operatorname {} pgcd (y, z)) = \ operatorname {} GCD (x, y, z) \ \ quad \\ \ operatorname {} LCM (\ operatorname {} LCM (x, y), z) = \ operatorname {} LCM (x, \ operatorname {} LCM (y, z) ) = \ operatorname {} LCM (x, y, z) \ quad \ end {matrix} \ right \} \ mbox {} pour tous x, y, z \ in \ mathbb {Z}.$

Parce que transformations linéaires sont des fonctions qui peuvent être représentées par des matrices de multiplication matricielle étant la représentation fonctionnelle de la composition, on peut conclure que la matrice immédiatement multiplication est associative.

Prendre le intersection ou le union de ensembles:

$\ Left. \ Begin {matrix} (A \ cap B) \ cap C = A \ cap (B \ cap C) = A \ cap B \ cap C \ quad \\ (A \ cup B) \ cup C = A \ tasse ( B \ cup C) = A \ cup B \ cup C \ quad \ end {matrix} \ right \} \ mbox {} pour tous les ensembles A, B, C.$

Si M est un certain ensemble et S désigne l'ensemble de toutes les fonctions de M à M, alors l'opération de composition fonctionnelle sur S est associative:

$(F \ circ g) \ circ h = f \ circ (g \ circ h) = f \ circ g \ circ h \ qquad \ mbox {} pour tous f, g, h \ S.$

Un peu plus généralement, compte tenu de quatre séries M, N, P et Q, avec h: M à N, g: P à N, et f: P à Q, puis

$(F \ circ g) \ circ h = f \ circ (g \ circ h) = f \ circ g \ circ h$

comme avant. En bref, la composition de cartes est toujours associative.

Considérons un ensemble de trois éléments, A, B, et C. L'opération suivante:

×	Un	B	C
+
Un	Un	Un	Un
B	Un	B	C
C	Un	Un	Un

est associatif. Ainsi, par exemple, A (BC) = (AB) C. Cette cartographie ne est pas commutative.

Non-associativité

Une opération binaire 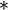$*$ sur un ensemble S qui ne satisfait pas à la loi associative est appelé non-associative. Symboliquement,

$(X * y) * z \ ne x * (y * z) \ qquad \ mbox {} pour un certain x, y, z \ in S.$

Pour une telle opération l'ordre d'évaluation de l'importance. soustraction , division et exponentiation sont des exemples bien connus des opérations non associatifs:

$\ Begin {matrix} (5-3) -2 \ ne 5- (3-2) \ quad \\ (4/2) / 2 \ ne 4 / (2/2) \ qquad \ qquad \\ 2 ^ { (1 ^ 2)} \ ne (2 ^ 1) ^ 2. \ quad \ qquad \ qquad \ end {matrix}$

En général, les parenthèses doivent être utilisés pour indiquer le ordre d'évaluation si une opération non-associative apparaît plus d'une fois dans une expression. Cependant, les mathématiciens se accordent sur un ordre particulier de l'évaluation pour plusieurs opérations non associatifs communs. Ce est tout simplement une convention syntaxique pour éviter parenthèses.

Une opération de gauche est une opération associative non associatif qui est classiquement évaluée de gauche à droite, ce est à dire,

$\ Left. \ Begin {matrix} x * y * z = (x * y) * z \ qquad \ qquad \ quad \, \\ w * x * y * z = ((w * x) * y) * z \ quad \ \ \ mbox {etc.} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ \ \, \ end {matrix} \ right \} \ mbox {} pour tous les w, x, y, z \ in S$

pendant qu'une opération associatif à droite est classiquement évaluée de droite à gauche:

$\ Left. \ Begin {matrix} x * y * z = x * (y * z) \ qquad \ qquad \ quad \, \\ w * x * y * z = w * (x * (y * z)) \ quad \ \ \ mbox {etc.} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ \ \, \ end {matrix} \ right \} \ mbox {} pour tous les w, x, y, z \ in S$

Les deux opérations gauche associatifs et à droite associatifs se produisent; des exemples sont donnés ci-dessous.

Plus d'exemples

Left-associatif opérations sont les suivantes.

Soustraction et la division des nombres réels:

$xyz = (xy) z \ qquad \ mbox {} pour tous x, y, z \ in \ mathbb {R};$

$x / y / z = (x / y) / z \ qquad \ qquad \ quad \ mbox {} pour tous x, y, z \ in \ mathbb {R} \ mbox {} avec y \ ne0, z \ ne0.$

Opérations droit associatifs sont les suivantes.

Exponentiation des nombres réels:

$x ^ {y ^ z} = x ^ {(y ^ z)}. \,$

La raison en est exponentiation de droit associatif est qu'une opération d'exponentiation gauche associative répétée serait moins utile. Apparences multiples pourraient (et devraient) être réécrites avec la multiplication:

$(X ^ y) ^ z = x ^ {(yz)}. \,$

Opérations non associatifs pour lesquels aucun ordre d'évaluation conventionnelle est définie sont les suivantes.

Prenant la paire moyenne des nombres réels:

${(X + y) / 2 + z \ over2} \ ne {x + (y + z) / 2 \ over2} \ ne {x + y + z \ over3} \ qquad \ mbox {pour certains} x, y, z \ in \ mathbb {R}.$

Prendre le complément relative des ensembles:

$(A \ barre oblique inverse B) \ barre oblique inverse C \ ne A \ barre oblique inverse (B \ barre oblique inverse C) \ qquad \ mbox {} pour certaines séries A, B, C.$

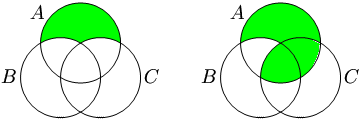
$Diagramme de Venn des compléments relatifs (A \ B) \ C et A \ (B \ C)$

La partie verte de la gauche diagramme de Venn représente (A \ B) \ C. La partie verte dans le diagramme de Venn droite représente A \ (B \ C).

En utilisant la notation associatif à droite pour Implication peut être motivé par exemple par Curry-Howard correspondance: voir par exemple comparaison des deux premiers axiomes du système de déduction Hilbert-style avec combinateurs base de la logique combinatoire.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Associative_property&oldid=202029355 "