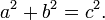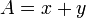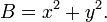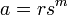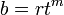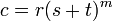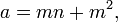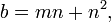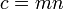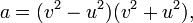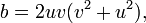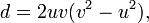Le dernier théorème de Fermat

L'édition 1670 du Diophante Arithmetica comprend le commentaire de Fermat, en particulier son «dernier théorème" (Observatio Domini Petri de Fermat).

Dans la théorie des nombres , le dernier théorème de Fermat (parfois appelé la conjecture de Fermat, en particulier dans les textes plus anciens) stipule qu'aucune trois positifs entiers a, b, et c peuvent satisfaire à l'équation a ⁿ + b ⁿ = c ⁿ pour chaque valeur entière de n supérieur à deux.

Ce théorème a été le premier conjecturé par Pierre de Fermat en 1637, célèbre dans la marge d'une copie de Arithmetica où il a affirmé qu'il avait une preuve qui était trop grand pour tenir dans la marge. Aucune preuve de succès a été publié jusqu'en 1995 malgré les efforts d'innombrables mathématiciens pendant les 358 années qui ont suivi. Le problème non résolu stimulé le développement de théorie algébrique des nombres dans le 19ème siècle et la preuve de la modularité théorème dans le 20e siècle. Il est parmi les plus célèbres théorèmes les dans le histoire des mathématiques et avant son 1995 était la preuve dans le Livre Guinness des Records du Monde pour "problèmes mathématiques les plus difficiles".

Histoire

Fermat n'a laissé aucune preuve de la conjecture pour tout n, mais il a fait preuve le cas particulier n = 4. Cela a réduit le problème à démontrer le théorème pour exposants n qui sont des nombres premiers . Au cours des deux prochains siècles (1637-1839), la conjecture a été prouvé que pour les primes 3, 5 et 7, bien que Sophie Germain se est avéré un cas particulier pour tous les nombres premiers inférieur à 100. Dans le milieu du 19e siècle, Ernst Kummer a prouvé le théorème pour nombres premiers réguliers. Se appuyant sur les travaux de Kummer et en utilisant des études informatiques sophistiqués, d'autres mathématiciens ont pu démontrer la conjecture pour tous les nombres premiers impairs jusqu'à quatre millions.

La preuve définitive de la conjecture pour tout n est venu à la fin du 20ème siècle. En 1984, Gerhard Frey a suggéré l'approche de prouver la conjecture par une preuve de la modularité théorème pour les courbes elliptiques . Se appuyant sur les travaux de Ken Ribet, Andrew Wiles réussi à prouver le théorème assez de modularité pour prouver le dernier théorème de Fermat, avec l'aide de Richard Taylor. La réalisation de Wiles a été largement rapportées par la presse populaire, et a été popularisé dans les livres et les programmes de télévision.

Contexte mathématique

Triplets pythagoriciens

Un triplet de Pythagore est un ensemble de trois entiers (a, b, c) qui satisfont un cas particulier de l'équation de Fermat (n = 2)

Des exemples de triplets de Pythagore comprennent (3, 4, 5) et (5, 12, 13). Il ya une infinité de ces triples, et les méthodes pour générer ces triples ont été étudiés dans de nombreuses cultures, en commençant par le Babyloniens et plus tard le grec ancien, Chinois et Indiens mathématiciens. L'intérêt traditionnel pour triplets pythagoriciens se connecte avec le théorème de Pythagore ; dans sa forme inverse, il stipule qu'un triangle avec des côtés de longueurs a, b, c et a une angle droit entre l'un et les jambes b lorsque les chiffres sont un triplet pythagoricien. Perpendiculairement avoir diverses applications de pratiques, telles que arpentage, la menuiserie, maçonnerie, et construction. Le dernier théorème de Fermat est une extension de ce problème à des puissances plus élevées, indiquant qu'aucune solution existe lorsque l'exposant 2 est remplacé par un entier supérieur.

Équations diophantiennes

Équation x ^{le n} de Fermat + y ⁿ = z ⁿ est un exemple d'une équation diophantienne. Une équation diophantienne est une équation polynomiale dans laquelle les solutions doivent être des entiers. Leur nom dérive du 3ème siècle Alexandrie mathématicien, Diophante, qui a développé des méthodes pour leur solution. Un problème diophantienne typique est de trouver deux entiers x et y tels que leur somme, et la somme de leurs carrés, égale deux nombres donnés A et B, respectivement:

Œuvre majeure de Diophante est le Arithmetica, dont une partie seulement a survécu. La conjecture de Fermat de son dernier théorème a été inspiré lors de la lecture d'une nouvelle édition de la Arithmetica, qui a été traduit en latin et publié en 1621 par Claude Bachet.

Équations diophantiennes ont été étudiés depuis des milliers d'années. Par exemple, les solutions de l'équation quadratique Diophantine x ² + y ² = z ² sont données par le Triplets pythagoriciens, l'origine résolus par les Babyloniens (c. 1800 BC). Solutions d'équations linéaires diophantiennes, tels que 26 x 65 + y = 13, peuvent être trouvés en utilisant le Euclidienne algorithme (c. 5ème siècle avant JC). Beaucoup Équations diophantiennes avoir une forme similaire à l'équation du dernier théorème de Fermat du point de vue de l'algèbre, en ce qu'ils ne ont pas de termes croisés mélange de deux lettres, sans partager ses propriétés particulières. Par exemple, il est connu qu'il existe une infinité d'entiers positifs x, y et z de telle sorte que x + y ^{n n} = z ^m où n et m sont nombres naturels relativement premiers.

La conjecture de Fermat

II.8 problème dans l'édition 1621 de la Arithmetica de Diophante. Sur la droite se trouve le célèbre marge qui était trop petite pour contenir la preuve alléguée de Fermat de son «dernier théorème".

II.8 du problème Arithmetica demande comment un certain nombre carré donné est divisé en deux autres places; en d'autres termes, une donnée de nombre rationnel k, pour des nombres rationnels u et v tels que k ² = u ² + v ^2. Diophante montre comment résoudre cette somme des carrés problème pour k = 4 (les solutions étant u = 16/5 et v = 12/5).

Autour de 1637, Fermat a écrit son dernier théorème dans la marge de son exemplaire de la Arithmetica côté de la somme des carrés problème de Diophante:

Bien que la preuve générale de Fermat est inconnue, sa preuve d'un cas (n = 4) par descente infinie a survécu. Fermat a posé les cas de n = 4 et n = 3 comme des défis à ses correspondants mathématiques, comme Marin Mersenne, Blaise Pascal , et John Wallis. Cependant, dans les trente dernières années de sa vie, Fermat jamais écrit de sa «preuve vraiment merveilleux" du cas général.

Après la mort de Fermat en 1665, son fils Samuel Clément-Fermat a produit une nouvelle édition du livre (1670) augmentée avec les commentaires de son père. La note de la marge est devenu connu comme le dernier théorème de Fermat, que ce était la dernière des théorèmes de Fermat revendiqués à rester à prouver.

Les épreuves pour les exposants spécifiques

Un seul preuve mathématique par Fermat a survécu, dans lequel Fermat utilise la technique de descente infinie de montrer que l'aire d'un triangle dont les côtés entiers ne peut jamais égaler la place d'un entier. Sa preuve est équivalent à démontrer que l'équation

n'a pas de solutions primitives en entiers (pas solutions de premiers entre eux deux à deux). À son tour, cela prouve le dernier théorème de Fermat pour le cas n = 4, puisque l'équation d'un ⁴ + b = c ^{4 4} peut être écrit comme c ⁴ - b = ^{4 (2) 2.}

Preuves alternatives de l'affaire n = 4 ont été développés plus tard par Frénicle de Bessy (1676), Leonhard Euler (1738), Kausler (1802), Peter Barlow (1811), Adrien-Marie Legendre (1830), Schopis (1825), Terquem (1846), Joseph Bertrand (1851), Victor Lebesgue (1853, 1859, 1862), Théophile Pepin (1883), Tafelmacher (1893), David Hilbert (1897), Bendz (1901), Gambioli (1901), Leopold Kronecker (1901), Bang (1905), Sommer (1907), Bottari (1908), Karel Rychlík (1910), Nutzhorn (1912), Robert Carmichael (1913), Hancock (1931), et Vrǎnceanu (1966).

Pour autre preuve pour n = 4 par descente infinie, voir Infini descente: non-solvabilité de r ² + ⁴ = ⁴ t. Pour diverses preuves pour n = 4 par descente infinie, voir Grant et Perella (1999), Barbara (2007), et Dolan (2011).

Après Fermat se est avéré le cas particulier n = 4, la preuve générale pour tout n exigeait seulement que le théorème être établi pour tous les exposants premiers impairs. En d'autres termes, il était nécessaire de prouver seulement que l'équation a + b ^{n n} = c ⁿ n'a pas de solutions entières (a, b, c) lorsque n est un nombre impair nombre premier . Ceci fait suite à cause d'une solution (a, b, c) pour un n donné est équivalente à une solution à tous les facteurs de n. À titre d'illustration, soit N pris en compte dans d et e, n = de. L'équation générale

un ⁿ + b = c ^{n n}

implique que (a ^j, b ^j, c ^d) est une solution pour l'exposant e

(A ^{d) e} + (b ^{d) e} = (c ^{d) e.}

Ainsi, pour prouver que l'équation de Fermat n'a pas de solutions pour n> 2, il suffit de prouver qu'il n'a pas de solution pour au moins un facteur premier de tous les n. Tous les entiers n> 2 contiennent un facteur de 4, ou un nombre premier impair, ou les deux. Par conséquent, le dernier théorème de Fermat peut être prouvé pour tout n se il peut être prouvé pour n = 4 et pour tous les nombres premiers p impair (le seul nombre premier est le numéro 2).

Dans les deux siècles suivants sa conjecture (1637-1839), le dernier théorème de Fermat a été prouvé pendant trois exposants premiers impairs p = 3, 5 et 7. Le cas p = 3 a été la première fois par Al-Khujandi (10ème siècle), mais sa démonstration du théorème était incorrecte. En 1770, Leonhard Euler a donné une preuve de p = 3, mais sa preuve en descente infinie contenait une lacune majeure. Cependant, depuis Euler se était révélé le lemme nécessaire pour compléter la preuve dans d'autres travaux, il est généralement crédité de la première preuve. Preuves indépendantes ont été publiées par Kausler (1802), Legendre (1823, 1830), Calzolari (1855), Gabriel Lamé (1865), Peter Guthrie Tait (1872), Günther (1878), Gambioli (1901), Krey (1909), Rychlík (1910), Stockhaus (1910), Carmichael (1915), Johannes van der Corput (1915), Axel Thue (1917), et Duarte (1944). Le cas p = 5 a été prouvé de façon indépendante par Legendre et Peter Dirichlet vers 1825. preuves alternatifs ont été développés par Carl Friedrich Gauss (1875, posthume), Lebesgue (1843), Lamé (1847), Gambioli (1901), Werebrusow (1905), Rychlík (1910), van der Corput (1915) et Guy Terjanian (1987). Le cas p = 7 a été prouvé par Lamé en 1839. Sa preuve assez compliqué a été simplifiée en 1840 par Lebesgue, et les preuves toujours plus simples ont été publiés par Angelo Genocchi en 1864, 1874 et 1876. preuves alternatifs ont été développés par Théophile Pépin (1876) et Edmond Maillet (1897).

Le dernier théorème de Fermat a également été prouvé pour les exposants n = 6, 10, et 14. Les preuves pour n = 6 ont été publiés par Kausler, Thue, Tafelmacher, Lind, Kapferer, Swift et Breusch. De même, Dirichlet et Terjanian chaque prouvé le cas n = 14, tandis que Kapferer et Breusch chaque prouvé le cas n = 10. Strictement parlant, ces preuves ne sont pas nécessaires, étant donné que ces cas découlent des preuves pour n = 3, 5 et 7, respectivement. Néanmoins, le raisonnement de ces preuves encore-exposant diffère de leurs homologues impair exposant. La preuve de Dirichlet pour n = 14 a été publié en 1832, avant 1839 la preuve de Lamé pour n = 7.

Beaucoup de preuves pour exposants spécifiques utilisent la technique de Fermat descente infinie, qui Fermat utilisé pour prouver le cas n = 4, mais beaucoup ne le font pas. Cependant, les détails et arguments auxiliaires sont souvent ad hoc et liés à l'exposant individuelle à l'étude. Depuis ils sont devenus de plus en plus compliqué que p augmenté, il semblait peu probable que le cas général du dernier théorème de Fermat pouvait être prouvé en se appuyant sur les preuves pour les exposants individuels. Bien que certains résultats généraux sur le dernier théorème de Fermat ont été publiés au début du 19ème siècle par Niels Henrik Abel et Peter Barlow, le premier travail important sur le théorème général a été fait par Sophie Germain.

Sophie Germain

Au début du 19e siècle, Sophie Germain a développé plusieurs nouvelles approches pour prouver le dernier théorème de Fermat pour tous les exposants. D'abord, elle a défini un ensemble de nombres premiers auxiliaires θ construits à partir de l'exposant premier p par l'équation θ = 2 ch 1, où h est tout entier non divisible par trois. Elle a montré que, si aucun des nombres entiers élevés à la puissance ^p-ième étaient (la condition de non-consécutivité) de modulo adjacent, alors θ doit diviser le produit xyz. Son but était d'utiliser induction mathématique pour prouver que, pour tout p donné, infinité de nombres premiers auxiliaires θ satisfait à la condition non-consécutivité et donc divisés xyz; depuis le xyz produit peut avoir au plus un nombre fini de facteurs premiers, cette preuve aurait établi le dernier théorème de Fermat. Même si elle a développé de nombreuses techniques pour établir la condition de non-consécutivité, elle n'a pas réussi dans son objectif stratégique. Elle a également travaillé à fixer des limites inférieures sur la taille de solutions à l'équation de Fermat pour un exposant p donné, une version modifiée de ce qui a été publié par Adrien-Marie Legendre. En tant que sous-produit de ce dernier travail, elle se est avérée Théorème de Sophie Germain, qui a vérifié le premier cas du dernier théorème de Fermat (à savoir, dans le cas où p ne divise pas xyz) pour chaque exposant premier impair inférieur à 100. Germain a tenté en vain de prouver le premier cas du dernier théorème de Fermat pour tous, même exposants, en particulier pour n = 2 p, qui a été prouvé par Guy Terjanian en 1977. En 1985, Leonard Adleman, Roger Heath-Brown et Étienne Fouvry prouvé que le premier cas du dernier théorème de Fermat détient pour une infinité de nombres premiers impairs p.

Ernst Kummer et la théorie des idéaux

En 1847, Gabriel Lamé présenté une preuve du dernier théorème de Fermat sur la base de l'affacturage l'équation x + y ^{p p p} = z dans les nombres complexes, en particulier la cyclotomique champ sur la base du racines de la numéro 1. Sa preuve ne ont pas, cependant, car il suppose à tort que ces nombres complexes peuvent être pris en compte uniquement en nombres premiers, semblables à des nombres entiers. Cet écart a été signalé immédiatement Joseph Liouville, qui plus tard a lu un papier qui a démontré cet échec de factorisation unique écrit par Ernst Kummer.

Kummer se est donné pour tâche de déterminer si le corps cyclotomique pourrait être généralisé pour inclure de nouveaux nombres premiers tels que la factorisation unique a été restauré. Il a réussi dans cette tâche par le développement du numéros idéales. En utilisant l'approche générale décrite par Lamé, Kummer a prouvé les deux cas du dernier théorème de Fermat pour tous nombres premiers réguliers. Cependant, il ne pouvait pas prouver le théorème pour les primes exceptionnelles ( primes irrégulières) qui se produisent conjecturalement environ 39% du temps; les seuls nombres premiers irréguliers inférieures à 100 sont 37, 59 et 67.

Mordell conjecture

Dans les années 1920, Louis Mordell posé une conjecture qui implique que l'équation de Fermat a au plus un nombre fini de solutions entières primitives non triviaux si l'exposant n est supérieur à deux. Cette conjecture a été prouvée en 1983 par Gerd Faltings, et est maintenant connu sous le nom Théorème de Faltings.

Les études computationnelles

Dans la seconde moitié du 20e siècle, les méthodes de calcul ont été utilisés pour étendre l'approche de Kummer aux nombres premiers irréguliers. En 1954, Harry Vandiver a utilisé une CSAO ordinateur pour prouver le dernier théorème de Fermat pour tous les nombres premiers jusqu'à 2521. En 1978, Samuel Wagstaff avait étendu ce à tous les nombres premiers inférieurs 125,000. En 1993, le dernier théorème de Fermat avait été éprouvée pour tous les nombres premiers moins de quatre millions d'euros.

Connexion avec les courbes elliptiques

La stratégie finalement couronnée de succès pour prouver le dernier théorème de Fermat était en prouvant la modularité théorème. La stratégie a été décrite par Gerhard Frey en 1984. Frey a noté que si l'équation de Fermat avait une solution (a, b, c) pour exposant p> 2, le correspondant courbe elliptique

y ² = x (x - un ^p) (x + ^p b)

aurait de telles propriétés inhabituelles que la courbe serait susceptible de violer le théorème de modularité. Ce théorème, d'abord conjecturé au milieu des années 1950 et affiné progressivement dans les années 1960, stipule que chaque courbe elliptique est modulaire, ce qui signifie qu'il peut être associé à un unique, forme modulaire.

Suivant cette stratégie, la preuve du dernier théorème de Fermat a nécessité deux étapes. Tout d'abord, il était nécessaire de montrer que l'intuition de Frey était correcte: que la courbe elliptique ci-dessus, si elle existe, est toujours non modulaire. Frey n'a pas réussi à prouver cette rigueur; la pièce manquante a été identifié par Jean-Pierre Serre. Cette pièce manquante, la soi-disant " epsilon conjectures ", a été prouvée par Ken Ribet en 1986. Deuxièmement, il était nécessaire de prouver un cas particulier du théorème de modularité. Ce cas particulier (pour courbes elliptiques semi-stables) a été prouvée par Andrew Wiles en 1995.

Ainsi, la conjecture epsilon a montré que la solution de l'équation de Fermat pourrait être utilisée pour générer une courbe elliptique semi-stable non modulaire, tandis que la preuve de Wiles a montré que toutes ces courbes elliptiques doivent être modulaire. Cette contradiction implique qu'il ne peut y avoir de solution à l'équation de Fermat, prouvant ainsi le dernier théorème de Fermat.

Démonstration générale de Wiles

Mathématicien britannique Andrew Wiles

La preuve de Ribet de la epsilon conjecture en 1986 accompli la première moitié de la stratégie de Frey pour prouver le dernier théorème de Fermat. Après audition de la preuve de Ribet, Andrew Wiles a décidé de se engager à accomplir la seconde moitié: prouver un cas particulier de la modularité théorème (alors connu comme la conjecture de Shimura-Taniyama) pour les courbes elliptiques semi-stables. Wiles a travaillé sur cette tâche pendant six ans dans le secret presque complète. Il a fondé son approche initiale sur son domaine d'expertise, Théorie d'Iwasawa Horizontal, mais d'ici l'été 1991, cette approche semblait insuffisante pour la tâche. En réponse, il a exploité un Euler système récemment développé par Victor et Kolyvagin Matthias Flach. Depuis Wiles était pas familier avec ces méthodes, il a demandé à son collègue de Princeton, Nick Katz, pour vérifier son raisonnement sur le semestre de printemps 1993.

À la mi-1993, Wiles était suffisamment confiant de ses résultats qu'il les présente en trois conférences prononcées sur Juin 21-23 1993, à la Isaac Newton Institute for Mathematical Sciences. Plus précisément, Wiles a présenté sa preuve de la conjecture de Shimura-Taniyama pour les courbes elliptiques semi-stables; avec la preuve de Ribet de la conjecture de epsilon, cela impliquait le dernier théorème de Fermat. Cependant, il est vite apparu que la preuve initiale de Wiles était incorrecte. Une partie essentielle de la preuve contenait une erreur dans une borne sur l'ordre d'un particulier groupe . L'erreur a été capturé par plusieurs mathématiciens arbitrage d manuscrit de Wiles y compris Katz, qui a alerté le 23 Août Wiles 1993.

Wiles et son ancien élève Richard Taylor a passé près d'un an à essayer de réparer la preuve, sans succès. Le 19 Septembre 1994, Wiles avait un éclair d'intelligence que la preuve pourrait être sauvé par retourner à son approche de la théorie d'Iwasawa horizontale originale, qu'il avait abandonné en faveur de l'approche Kolyvagin-Flach. Le 24 Octobre 1994, Wiles a présenté deux manuscrits, «courbes elliptiques modulaires et le dernier théorème de Fermat» et «propriétés théoriques de sonnerie de certaines algèbres de Hecke", dont la seconde a été co-écrit avec Taylor. Les deux documents ont été examinées et publiées que l'intégralité de la question de mai 1995 Annales de mathématiques. Ces documents établis le théorème de modularité pour les courbes elliptiques semi-stables, la dernière étape à prouver le dernier théorème de Fermat, 358 années après qu'il a été conjecturé.

Exposants autres que des nombres entiers positifs

Exposants rationnels

Toutes les solutions de l'équation diophantienne 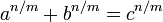lorsque n = 1 ont été calculés par Lenstra en 1992. Dans le cas où la m ^ième racines doivent être réels et positifs, toutes les solutions sont donnés par

pour les entiers positifs r, s, t avec s et t premiers entre eux.

En 2004, pour n> 2, Bennett, verre, et Szekely prouvé que si pgcd (n, m) = 1, alors il existe des solutions entières si et seulement si 6 divise m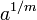, 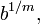et , et 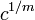sont différents 6e racines complexes du même nombre réel.

Exposants négatifs

n = -1

Tous les premiers entre eux (par paire) solutions entières primitifs à 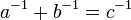peut se écrire

pour le positif, Nombres premiers entre eux m, n.

n = -2

Le cas n = -2 a aussi une infinité de solutions, et ceux-ci ont une interprétation géométrique en termes de triangles rectangles avec des côtés entiers et une altitude entier à l'hypoténuse. Toutes les solutions primitives à sont donnés par

pour les premiers entre eux entiers u, v avec v> u. L'interprétation géométrique est que a et b sont des nombres entiers les jambes d'un triangle rectangle et d est la hauteur entière de l'hypoténuse. Ensuite, l'hypoténuse lui-même est le nombre entier

si (a, b, c) est un Triplet pythagoricien.

Integer n <-2

Il n'y a pas de solutions en entiers pour 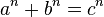pour n entier <-2. Se il y avait, l'équation pourrait être multiplié par par 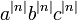obtenir , Ce qui est impossible par le dernier théorème de Fermat.

Avez-Fermat possède une preuve générale?

Les techniques mathématiques utilisés dans la preuve «merveilleux» de Fermat sont inconnus. Seulement une preuve détaillée de Fermat a survécu, la preuve ci-dessus qu'aucune trois entiers premiers entre eux (x, y, z) satisfont l'équation x ⁴ - ⁴ y = z ^2.

La preuve de Taylor et Wiles se appuie sur des techniques mathématiques développées au XXe siècle, ce qui serait inconnu de mathématiciens qui avaient travaillé sur le dernier théorème de Fermat même un siècle plus tôt. Prétendue «preuve merveilleuse" de Fermat, par comparaison, aurait dû être élémentaire, donné connaissance mathématique du temps, et ainsi ne aurait pas été la même que la preuve de Wiles. La plupart des mathématiciens et historiens des sciences douter que Fermat avait une preuve valable de son théorème pour tous les exposants n.

Harvey Friedman grande conjecture implique que le dernier théorème de Fermat peut être prouvé en arithmétique élémentaire, une forme plutôt faible de l'arithmétique avec addition, multiplication, exponentiation, et une forme limitée d'induction pour les formules avec quantificateurs bornés. Une telle preuve serait élémentaire mais peut-être trop long à écrire.

Des prix en argent

En 1816 et de nouveau en 1850, le Académie française des sciences a offert un prix pour une preuve générale du dernier théorème de Fermat. En 1857, l'Académie reçu 3000 francs et une médaille d'or à Kummer pour ses recherches sur le nombre idéal, même se il ne avait pas présenté une entrée pour le prix. Un autre prix a été offert en 1883 par l'Académie de Bruxelles.

En 1908, le mathématicien industriel et amateur allemand Paul Wolfskehl légué 100 000 marques à l'Académie des sciences de Göttingen qui seront offerts comme prix pour une preuve complète du dernier théorème de Fermat. Le 27 Juin 1908, l'Académie a publié neuf règles pour l'attribution du prix. Entre autres choses, ces règles exigent que la preuve sera publié dans une revue à comité de lecture; le prix ne serait pas attribué que deux ans après la publication; et qu'aucun prix serait donné après le 13 Septembre 2007, à peu près un siècle après la compétition a commencé. Wiles recueilli l'argent du prix Wolfskehl, alors vaut $ 50 000, le 27 Juin 1997.

Avant la preuve de Wiles, des milliers de preuves incorrectes ont été soumises au comité Wolfskehl, se élevant à environ 10 pieds (3 mètres) de correspondance. Dans la première année (1907-1908), 621 tentatives de preuves ont été présentées, bien que par les années 1970, le taux de soumission avait diminué à environ 3-4 tentatives de preuves par mois. Selon F. Schlichting, un examinateur Wolfskehl, la plupart des preuves ont été basées sur les méthodes enseignées dans les écoles élémentaires, et souvent soumis par des «personnes ayant une formation technique mais une carrière échoué". Dans les mots de l'historien mathématique Howard Eves, "le dernier théorème de Fermat a la particularité singulière d'être le problème mathématique pour lequel le plus grand nombre de preuves incorrectes ont été publiés."

Dans la culture populaire

• Un épisode de la série de télévision Star Trek: The Next Generation, intitulé " La Royale ", se réfère au théorème dans le premier acte Riker visite capitaine Jean-Luc Picard dans sa chambre prête à signaler seulement pour trouver Picard énigmatique sur le dernier théorème de Fermat l'intérêt de Picard dans ce théorème va au-delà de la difficulté du puzzle;.. Il aussi se sent humilié que malgré leur technologie de pointe, ils sont encore incapables de résoudre un problème posé par un homme qui ne avait pas l'ordinateur. Un épisode Star Trek: Deep Space 9, intitulé " Facettes ", se réfère au théorème ainsi. Dans une scène impliquant O'Brien, Tobin Dax mentionne les travaux sur sa propre tentative pour résoudre le dernier théorème de Fermat continue.
• "La Preuve" - Nova ( PBS) documentaire sur la preuve d'Andrew Wiles du dernier théorème de Fermat.
• Le 17 Août 2011, un Google doodle a été montré sur la page d'accueil Google, montrant un tableau noir avec le théorème sur elle. Lorsque plané au-dessus, il affiche le texte "je ai découvert une preuve vraiment merveilleux de ce théorème, dont ce doodle est trop petit pour contenir." Ce est une référence à la note faite par Fermat en marge de Arithmetica. Il commémore la naissance 410e anniversaire de de Fermat.
• Dans le livre La Fille qui rêvait d'un bidon d'essence et d'une allumette, Lisbeth Salander personnage principal devient obsédé par le théorème dans les premiers chapitres du livre. Son effort continu pour venir avec une preuve de sa propre est un sous-terrain en cours d'exécution à travers l'histoire, et est utilisé comme un moyen de démontrer son intelligence exceptionnelle. A la fin elle arrive avec une preuve (la preuve réelle ne est pas sélectionnée dans le livre). Mais après avoir reçu une balle dans la tête et survivant, elle a perdu la preuve.
• Dans le Harold Ramis re-make du film Bedazzled, avec Brendan Fraser et Elizabeth Hurley, le dernier théorème de Fermat semble écrit sur le tableau dans la classe que le protagoniste Elliot se retrouve téléporté à après qu'il abandonne son quatrième souhait échoué. Dans le commentaire du réalisateur pour la sortie en DVD, directeur Ramis commente que personne n'a semblé remarquer que l'équation sur la carte est le dernier théorème de Fermat.
• Dans Doctor Who , Saison 5 Episode 1 " The Eleventh Hour ", le Docteur transmet une preuve du dernier théorème de Fermat en le tapant dans quelques secondes sur l'ordinateur portable de Jeff de prouver son génie à une collection de chefs de file mondiaux discuter de la dernière menace pour la race humaine. Cela implique que le docteur savait une preuve qui était assez courte et facile pour les autres à comprendre.
• En The IT Crowd, série 3 Episode 6 " Calendrier Geeks "dernier théorème de Fermat est référencé au cours d'une séance photo pour un calendrier sur les geeks et les réalisations en sciences et en mathématiques.
• La chanson "Baby Genius Bizarro» par MC Frontalot contient les paroles "Et aucune poussière retombée quand elle avait réfuté Fermat en trouvant A ³ + B = C ³ que ^trois".
• Dans le manga et l'anime série de Zatch Bell! Une des questions du portier Unko Tintin était de prouver le dernier théorème de Fermat. Le protagoniste principal a réussi à l'éviter en se demandant si Unko Tintin pourrait répondre lui-même, qu'il ne pouvait pas.