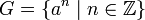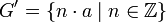Groupe (mathématiques)
À propos de ce écoles sélection Wikipedia
Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?
Un groupe est l'un des objets fondamentaux d'études dans le domaine des mathématiques connues comme l'algèbre abstraite . La branche de l'algèbre qui étudie les groupes se appelle la théorie des groupes . La théorie des groupes a des applications étendues dans les mathématiques, les sciences et l'ingénierie. De nombreuses structures algébriques tels que les champs et les espaces vectoriels peuvent être définis de manière concise en termes de groupes, et la théorie de groupe fournit un outil important pour étudier la symétrie , depuis les symétries de tout objet forment un groupe. Groupes sont donc des abstractions essentielles dans les branches de la physique impliquant symétrie principes, tels que la relativité , la mécanique quantique et la physique des particules . De plus, leur capacité à représenter géométriques transformations trouve des applications en chimie , infographie, et d'autres domaines.
| La théorie des groupes |
|---|
Notions de base
homomorphismes de groupe
|
Groupes finis
Classification des finie groupes simples
Groupes Mathieu
Groupes Conway
Groupes Janko
Groupes Fischer
|
Groupes modulaires
|
Topologique / groupes de Lie
Groupe de Lie de dimension infinie
|
Groupes algébriques |
De nombreuses structures étudiées en mathématiques se avèrent être des groupes. Il se agit notamment des systèmes familiers de nombre, telles que: les nombres entiers , les nombres rationnels , les nombres réels , et les nombres complexes sous plus, ainsi que les rationnels non nuls, réels, et les nombres complexes sous la multiplication. Autres exemples importants sont: le groupe de non-singuliers matrices sous la multiplication, et le groupe de fonctions inversibles dans la composition . La théorie des groupes permet aux propriétés de ces structures à étudier dans un cadre général.
Définition
Un groupe (G, *) est un Set G avec un opération binaire * qui satisfait les quatre suivantes axiomes:
- Fermeture: Pour tout a, b dans G, le résultat d'une * b est aussi dans G.
- Associativité : Pour tout a, b et c dans G, (a * b) * c = a * (b * c).
- élément de l'identité: Il existe un élément e dans G tel que pour tout a dans G, e * a = a * e = a.
- Élément Inverse: Pour chaque un à G, il existe un élément b de G tel que b = a * b * a = e, où e est un élément d'identité.
Certains textes omettent l'exigence explicite de la fermeture, depuis la fermeture du groupe résulte de la définition d'un opération binaire.
En utilisant la propriété de l'élément d'identité, il peut être montré qu'un groupe a exactement un élément d'identité. Voir la preuve ci-dessous.
L'inverse d'un élément a peut également être démontré unique, et il est généralement écrit un -1 (mais voir l' notation ci-dessous pour les groupes additive écrites).
Un groupe (G, *) est souvent notée simplement G où il n'y a pas d'ambiguïté quant à ce que l'opération est.
Illustration de la définition

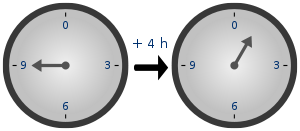
Un exemple va expliquer certaines propriétés de groupes. Considérons un carré . Nous sommes intéressés par les symétries de la place. Il existe des types de symétries suivantes:
- rotation d'environ 90 °, 180 ° et 270 ° (sens horaire). Nous allons écrire ces symétries que la pourriture 90 °, 180 ° pourrir et pourrir 270 °, respectivement. A noter que les rotations dans le sens horaire contre-sont inclus ici, par exemple en rotation dans le sens horaire de 270 ° de rotation est égale à 90 ° dans le sens antihoraire.
- réflexion le long de la ligne médiane verticale ou horizontale, ou le long des deux diagonales. Ecrivons les réflexions que ref V, ref H, ref D1 et D2 ref, respectivement.
- Enfin, l'opération id identiques laissant tout inchangé, ce est aussi une symétrie.
Tous les garder la forme du carré inchangé. (Dans les images, les sommets sont colorés seulement pour faire les opérations claires).
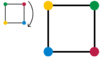 |  |  |  |  | 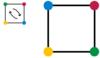 |  |
| Rotation vers la droite de 90 ° à 90 ° rot | Rotation vers la droite de 180 ° 180 ° rot | Rotation vers la droite de 270 ° 270 ° rot | Réflexion sur la ref vertical V | Réflexion sur la ref horizontal H | La réflexion le long d'une diagonale D1 ref | La réflexion le long de l'autre diagonale D2 ref |
Cet ensemble G des symétries est un exemple pour un groupe, la soi-disant . groupe dièdre d'ordre 8 étant un groupe signifie ce qui suit:
- Deux symétries peuvent être composés, soit donné deux symétries a et b, nous pouvons d'abord effectuer un, puis b et le résultat sera toujours une symétrie. Nous écrivons le résultat b * a (qui signifie «b après une"). Par exemple, la rotation de 270 °, puis par rotation de 180 ° est égal à une rotation de 90 °, ce est à dire en utilisant les symboles ci-dessus, nous avons
- rot 180 ° * ° = 270 rot rot 90 °.
- Dans un langage plus formel, G est doté d'un * opération binaire, soit deux éléments peut être composé à un troisième élément.
Appliqué à cet exemple le groupe, la définition se lit:
- Associativité : étant donné trois éléments a, b et c de G, (a * b) * c = a * (b * c).
- élément de l'identité: Il existe un élément e dans G tel que pour tout a dans G, e * a = a * e = a. Dans l'exemple, e est que la symétrie qui laisse tout inchangé.
- Élément Inverse: Pour chaque un à G, il existe un élément b de G tel que b = a * b * a = e, où e est un élément d'identité. Dans l'exemple, tourner un angle horaire donnée, puis en rotation par le même angle dans le sens antihoraire laissera la place inchangé et la même chose est vrai si nous inversons l'ordre, ce est à dire d'abord dans le sens antihoraire, puis dans le sens horaire. En outre, ce qui reflète le long d'une diagonale, par exemple, peut être inversée en appliquant à nouveau la même réflexion. Dans symboles:
- Rot 270 ° * rot 90 ° = 90 ° * rot rot 270 ° = id et ref D1 * ref D1 = id.
Histoire
Des groupes de permutations étaient déjà à l'étude dans le 18ème siècle et ont été appliquées pour résoudre les problèmes dans la théorie des équations. Cependant, la notion formelle d'un groupe n'a pas été publié jusqu'à la fin du 19ème siècle , et à ce moment les groupes avait trouvé des applications dans la théorie des nombres ainsi que dans la géométrie .
Concepts de base en théorie des groupes
Sous-groupes
Un sous-ensemble H ⊂ G est appelé le sous-groupe si la restriction de * H est une opération de groupe sur H. En d'autres termes, il se agit d'un groupe à l'aide de la restriction de l'opération définie sur G. Dans l'exemple ci-dessus, les rotations constituent un sous-groupe, étant donné qu'une rotation composée avec une rotation est encore une rotation.
Le test de sous-groupe est une condition nécessaire et suffisante pour un sous-ensemble H d'un groupe G d'être un sous-groupe: il suffit de vérifier que g -1 h ∈ H pour tout g, h ∈ H. Le fermeture, dans le cadre de l'opération de groupe et d'inversion, de ne importe quel sous-ensemble non vide d'un groupe est un sous-groupe.
Si G est un groupe fini, alors il en est H. En outre, l'ordre de H divise l'ordre de G ( Le théorème de Lagrange).
Les pouvoirs d'un élément d'un et leurs inverses (ce est-a 0 = e, a, a 2, a 3, a 4, ..., -1, -2, -3, -4 un, ...) toujours former un sous-groupe de l'ensemble du groupe. Il est dit que un sous-groupe qui génère.
Un sous-groupe H définit toujours un ensemble de gauche et de droite cosets. Étant donné un élément g arbitraire dans G, le classe à gauche de H contenant g est
et le droit coset de H contenant g est
L'ensemble des classes à gauche de H forme une partition des éléments de G; ce est, deux classes à gauche sont égaux ou avoir un vide intersection . La même chose est vraie des bonnes cosets de H. En général, les classes à gauche de H ne sont pas nécessairement égales aux classes à droite de H. Si ce est le cas que pour tout g dans G, gH = Hg, alors H est dit être un sous-groupe normal.
groupes quotients
Si N est un sous-groupe de G, l'ensemble de ses classes à gauche et classes à droite sont les mêmes et l'on peut parler simplement de l'ensemble des classes à de N. Dans ce cas, l'ensemble de co-ensembles de N peut être équipé d'une opération (parfois appelé co-ensemble de multiplication ou addition de co-ensemble) pour former un nouveau groupe, appelé le groupe quotient G / N. L'opération entre les classes à se comporte de la plus belle façon possible: (Ng) · (NH) = N (gh) pour tout g et h dans G. Notez que l'ensemble conjugué N se sert de l'identité de ce groupe, et l'inverse de Ng dans le groupe de quotient est (Ng)  = N (g
= N (g  ).
).
Groupes simples
Si un groupe G ne est pas le groupe trivial et de ses sous-groupes seulement normales sont le groupe trivial et le groupe lui-même, il est appelé un groupe simple. Avec la notion de groupes quotients, elle peut être formulée de manière équivalente comme: Un groupe avec seulement le groupe trivial et le groupe lui-même comme groupes quotients est simple.
homomorphismes de groupe
Si G et H sont deux groupes, un groupe homomorphisme f est une application f: G → H qui préserve la structure des groupes en question. La structure des groupes étant déterminé par l'opération de groupe, ceci signifie ce qui suit: si g et k sont tous deux des éléments en G, puis
- f (gk) = f (g) f (k).
Cette condition garantit que f (G 1) = H 1, et aussi f (g) = f -1 (g -1) pour tout g dans G.
Deux groupes G et H sont appelés isomorphes se il existe un homomorphisme du groupe f entre G et H, qui est à la fois surjective (sur) et injective (one-to-one).
Le noyau d'un homomorphisme f est noté ker f et est l'ensemble des éléments de G qui sont mappés à l'identité dans H. Ce est-ker f = {g en G: f (g) = 1 H}. Le noyau d'un homomorphisme est toujours un sous-groupe normal. Le Première isomorphisme Théorème indique que le image d'un homomorphisme du groupe, f (G) est isomorphe au groupe quotient G / ker f. Un fait utiles concernant homomorphismes est qu'ils sont injective si et seulement si leur noyau est trivial (ie ker f = {1} G).
Groupes abéliens
Un groupe 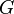 est dit être abélien ou commutative, si l'opération répond à la loi commutative. Autrement dit, pour toute
est dit être abélien ou commutative, si l'opération répond à la loi commutative. Autrement dit, pour toute 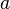 et
et  en
en 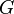 ,
,  . Sinon, le groupe est appelé non commutatif ou non-commutative. Le nom "abélien» vient du mathématicien norvégien Niels Abel. L'exemple ci-dessus des symétries de la place est non-abélienne, parce
. Sinon, le groupe est appelé non commutatif ou non-commutative. Le nom "abélien» vient du mathématicien norvégien Niels Abel. L'exemple ci-dessus des symétries de la place est non-abélienne, parce
- pourrir 90 ° * ref = V ref D2 de ref D1 = ref V * pourriture 90 ° les
Le centre d'un groupe est un sous-groupe constitué par les éléments qui commutent avec tous les autres éléments dans le groupe. Dans un groupe commutatif le centre est l'ensemble du groupe; à l'autre extrême, il ya des groupes dont le centre est trivial, ce est à dire qu'il ne se compose que de l'élément d'identité.
Les groupes cycliques
Un groupe cyclique est un groupe dont les éléments peuvent être successif généré par composition de l'opération de groupe étant appliqué à un seul élément de ce groupe. Un élément de cette propriété est appelée un générateur ou d'un élément primitif du groupe. Les groupes cycliques sont abélien.
Un groupe cyclique multiplicatif dans laquelle G est le groupe, et a est un générateur:
Un groupe cyclique additif, avec générateur d'une:
Si la composition successive de l'opération définissant le groupe est appliqué à un élément non primitif du groupe, un sous-groupe cyclique est généré. Selon Le théorème de Lagrange, l'ordre du sous-groupe cyclique divise l'ordre du groupe. Ainsi, si l'ordre d'un groupe fini est premier , l'ensemble de ses éléments, à l'exception du identité, sont des éléments primitifs du groupe.
Ordre de groupes et éléments
Le commande d'un groupe G, généralement désigné par | G | ou occasionnellement par o (G), est le nombre d'éléments de l'ensemble G. Si l'ordre ne est pas fini, alors le groupe est un groupe infini, noté | G | = ∞.
La commande d'un élément dans un groupe G est le nombre entier positif n de telle sorte que a n = e, où n représente un 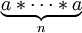 , À savoir l'application de l'opération de * n copies de la valeur a. (Si * représente la multiplication, puis a n correspond à la n ième puissance de a.) Si un tel n existe, alors l'ordre de un est dit être infini. La commande d'un élément est le même que l'ordre du sous-groupe cyclique généré par cet élément.
, À savoir l'application de l'opération de * n copies de la valeur a. (Si * représente la multiplication, puis a n correspond à la n ième puissance de a.) Si un tel n existe, alors l'ordre de un est dit être infini. La commande d'un élément est le même que l'ordre du sous-groupe cyclique généré par cet élément.
L'ordre du groupe de l'échantillon ci-dessus est de huit, de l'ordre de 90 ° pourriture est quatre, parce tourner 4 fois par 90 ° ne est pas rien changer. L'ordre des éléments de réflexion ref V, etc. est deux.
Notations et remarques
opération de groupe
Les groupes peuvent utiliser la notation différente selon le contexte et le fonctionnement du groupe.
- Groupes additifs utilisent + pour désigner plus, et le signe moins - pour désigner inverses. Par exemple, un + (- a) = 0 dans Z.
- Groupes multiplicatifs utilisent *,
 Ou le symbole plus général «composition»
Ou le symbole plus général «composition»  pour désigner la multiplication et l'exposant -1 pour désigner inverses. Par exemple, un * -1 = 1. Il est très fréquent de laisser tomber le * et il suffit d'écrire aa -1 place.
pour désigner la multiplication et l'exposant -1 pour désigner inverses. Par exemple, un * -1 = 1. Il est très fréquent de laisser tomber le * et il suffit d'écrire aa -1 place. - Groupes de fonctions utilisent • pour désigner la composition de fonctions, et l'exposant -1 pour désigner inverses. Par exemple, g • g -1 = e. Il est très fréquent de laisser tomber le • et il suffit d'écrire gg -1 place.
Omettant un symbole pour une opération est généralement acceptable, et laisse au lecteur le soin de connaître le contexte et le fonctionnement du groupe.
Lors de la définition des groupes, il est solfège à utiliser parenthèses dans la définition du groupe et son fonctionnement. Par exemple, (H +) représente le groupe formé par l'ensemble H avec addition comme opération de groupe. Pour des groupes comme (Z n, +) et (F q *, *), le groupe multiplicatif des éléments non nuls dans le corps fini F q, il est courant de déposer les parenthèses et le fonctionnement (depuis une seule opération rend ces mis en un groupe), que Z n et F q *. Il est également bon de se référer à un groupe par son identificateur de jeu, par exemple H ou 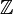 Ou pour définir le groupe en notation set-constructeur, pourvu qu'il soit clair quelle opération groupe est destiné.
Ou pour définir le groupe en notation set-constructeur, pourvu qu'il soit clair quelle opération groupe est destiné.
élément d'identité
En utilisant la propriété de l'élément d'identité, il peut être montré qu'un groupe a exactement un élément d'identité. Par conséquent, on parle généralement de l'identité: supposent à la fois e et f sont des éléments d'identité. Ensuite, parce que f est une (à droite) l'identité élément e * f = e, et parce que e est un (à gauche) l'identité élément e * f = f, où e = f.
L'élément d'identité électronique est parfois appelé «l'élément neutre", et est parfois désigné par un autre symbole, en fonction du groupe:
- Dans les groupes multiplicatifs, l'élément d'identité peut être désigné par une.
- Dans inversible les groupes de la matrice, l'élément d'identité est habituellement désignés par I ou Id.
- Dans les groupes d'additifs, l'élément d'identité peut être désigné par 0.
- Dans les groupes de fonctions, l'élément d'identité est habituellement désignée par f 0.
Si S est un sous-ensemble de G et x un élément de G, puis, dans la notation multiplicatif, XS est l'ensemble de tous les produits {xs: s en S}; De même, la notation Sx = {sx: s en S}; et pour deux sous-ensembles S et T de G, nous écrivons ST pour {er: s dans S, t en T}. Dans notation additive, nous écrivons x + S, S + x, et S + T pour les ensembles respectifs (voir cosets).
Inverse
L'inverse d'un élément A peut aussi être démontrée unique, et il est généralement écrit un -1 ou - a, selon le contexte. Supposons donné un inverse l et un autre inverse r. Puis
- l = l * e = l * (a * r) = (L * a) * r = e * r = r.
En outre, si dans un groupe, nous savons seulement que b * a = e, alors cela suffit pour conclure que b est l'élément inverse d'une (depuis un inverse recto-verso d'une garantie est d'exister, puis b doit être égale à il). De même a * b = e suffit à la même conclusion.
(Cependant, un ensemble avec une opération binaire peut comporter de nombreux éléments d'identité de gauche ou de nombreux éléments d'identité bonnes, à condition qu'il ne en a pas du genre opposé: prendre exemple sur aucun ensemble de l'opération définie par un * b = b, puis ne importe quel élément est un élément de l'identité gauche, mais aucune ne est un élément de l'identité droite même dans un monoïde un élément peut avoir plusieurs éléments inverses gauche, à condition qu'il n'a pas d'éléments bons inverses (et vice versa):. l'ensemble des cartes à partir d'un ensemble infini X lui-même est un monoïde dans la composition de fonctions, dans lequel chaque carte injective a un inverse à gauche, et chaque application surjective a un inverse à droite, mais aucun de ces inverses est unique en général. Pourtant, si tous les éléments dans un monoïde ont un inverse à gauche, le monoid peut être démontré un groupe.)
Associativité
Pour une séquence de facteurs multiples dans un ordre donné, on peut former un produit de nombreuses façons différentes en insérant entre parenthèses; Toutefois, par plusieurs applications de la propriété d'associativité, toute deux d'entre eux peuvent être démontré égale. Pour cette raison, l'expression
- 1 *, 2 * ··· * un n
est sans ambiguïté et les parenthèses sont généralement omis dans ces expressions. En conséquence, il ne est presque jamais nécessaire d'invoquer explicitement la propriété d'associativité.
Des variantes de la définition
Certaines définitions d'un groupe utilisent conditions apparemment plus faibles de l'identité et des éléments inverses. Au lieu d'exiger un élément d'identité recto-verso, on peut séparément exiger l'existence d'un élément de l'identité gauche et à droite, et de même on peut séparément exiger l'existence d'un des éléments inverses gauche et droite: dans les deux cas, les éléments de gauche et de droite peut être montré être la même (et chacun est unique).
Des exemples de groupes
Les entiers sous plus
Le groupe sans doute le plus connu est le groupe des entiers sous plus . On peut penser à des axiomes d'un groupe étant calqué sur les propriétés des nombres entiers Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...} , conjointement avec l'opération de groupe "+", qui désigne, comme d'habitude, l'addition. Les axiomes à vérifier sont:
- Fermeture: si a et b sont des nombres entiers alors a + b est un nombre entier.
- Associativité: si a, b, et c sont des nombres entiers, alors (a + b) + c = a + (b + c).
- Elément d'identité: 0 est un nombre entier et pour tout entier a, 0 + a = a + 0 = a.
- Éléments inverses: Si a est un nombre entier, le nombre entier - A satisfait les règles inverses: a + (- a) = (- a) + a = 0.
Ce groupe est aussi parce abélien a + b = b + a.
Si l'on prolonge en outre par cet exemple considérant les deux des nombres entiers avec addition et de multiplication, il forme une structure algébrique plus complexe appelée anneau. (Mais, notez que les nombres entiers avec multiplications ne sont pas un groupe.)
Certains groupes multiplicatifs
Le terme groupe multiplicatif désigne des groupes dont le fonctionnement découle de multiplication d'une certaine manière (en fonction du contexte).
Les entiers de moins de multiplication
Pour commencer, nous donnons un contre: les nombres entiers avec l'opération de multiplication, notée "·". Selon la notation générale, ce est noté (Z, ·). Il répond à la clôture, associativité et d'identité axiomes, mais ne parvient pas à avoir inverses: il ne est pas vrai que chaque fois qu'un est un nombre entier, il existe un entier b tel que ab = ba = 1. Par exemple, a = 2 est un entier, mais la seule solution de l'équation ab = 1 dans ce cas est b = 1/2. Nous ne pouvons pas choisir b = 1/2 parce moitié ne est pas un nombre entier. Etant donné que chaque élément de pas (Z, ·) présente un inverse (multiplicatif), (Z, ·) ne est pas un groupe. Il est, cependant, un commutative monoid, qui est une structure semblable à un groupe, mais ne nécessite pas d'éléments inverses.
Les nombres rationnels non nuls
Le étape naturelle pour remédier à cette envisage l'ensemble des nombres rationnels Q, l'ensemble de toutes les fractions de nombres entiers a / b, où a et b sont des nombres entiers et b est non nul, et l'opération de multiplication, à nouveau désigné par "·". Étant donné que le nombre rationnel de 0 n'a pas inverse multiplicatif, (Q, ·), comme (Z, ·), ne est pas un groupe.
Cependant, si nous utilisons à la place l'ensemble de tous les nombres rationnels non nulle Q \ {0}, puis (Q \ {0}, ·) ne forment un groupe abélien. En effet, fermeture, associativité et d'éléments d'identité axiomes sont faciles à vérifier et suivre des propriétés des nombres entiers (nous ne perdons pas de fermeture en supprimant zéro, parce que le produit de deux nombres rationnels non nuls ne est jamais nul). Enfin, l'inverse de a / b est b / a, donc l'axiome de l'élément inverse est satisfaite.
De même que les nombres entiers forment un anneau, les nombres rationnels forment la structure algébrique d'un champ, permettant les opérations d'addition, soustraction, multiplication et division.
Groupes multiplicatifs cycliques
En (Q, ·), il ya les sous-groupes cycliques
- G = {a n, n ∈ Z} ⊂ Q
où N est le n ième exponentiations de l'élément primitif a de ce groupe. Par exemple, si a est 2, alors
Ce groupe est un exemple d'un groupe abélien libre de une rang: le rang est une, car G est engendré par un élément (ou de manière équivalente un a -1) et l'indice d'égouttage se réfère au fait qu'aucune les relations entre les pouvoirs de ce générateur se produisent. Par conséquent, G, est isomorphe au groupe de nombres entiers (sous plus) présenté ci-dessus.
Consindering le groupe
- {A n, n ∈ Z / m Z},
le module m lie le groupe dans un ensemble fini avec un ensemble non-fractionnée d'éléments, depuis l'inverse (et  , Etc.) serait dans l'ensemble.
, Etc.) serait dans l'ensemble.
Les entiers non nuls modulo un premier
Les classes non nuls d'entiers modulo p, un nombre premier , forment un groupe pour la multiplication. Le produit de deux entiers dont aucun ne est divisible par p ne est pas divisible par p soit (car p est premier), ce qui montre que l'ensemble des classes indiqué est fermé sous la multiplication. Associativité est clair, et la classe de 1 est l'identité pour la multiplication, il reste à prouver, ce est que chaque élément a un inverse: étant donné un entier a pas divisible par p, il faut trouver un entier b tel que
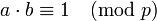 .
.
Ceci peut être démontré en utilisant le L'algorithme d'Euclide, par exemple. En fait, cet exemple est similaire à (Q \ {0}, ·) ci-dessus, car il se révèle être le groupe d'éléments non nuls dans la champ fini F p. Cependant, il est nettement différent du second groupe cyclique multiplicatif mentionné ci-dessus.
Groupes finis
Si le nombre d'éléments d'un groupe G est fini, alors G lui-même est appelé groupe fini. Ce qui précède groupe dièdre d'ordre 8 est un exemple. Deux classes importantes sont les suivantes:
- (abéliennes) les groupes cycliques Z / n Z traitées ci-dessus. Tout groupe fini abélien est un ensemble fini somme directe de groupes de ce genre, cela fait partie de la théorème fondamental de groupes abéliens de type fini.
- la groupe symétrique S N: il se agit du groupe de permutations de N lettres. Par exemple, le groupe symétrique sur 3 lettres S 3 est le groupe constitué de tous les swaps possibles des trois lettres ABC, ce est à dire contient les éléments ABC, ACB, ..., jusqu'à l'ABC, au total six (ou 3 factoriels ) éléments. Parallèlement au groupe de symétries de la place ci-dessus, S 3 peut également être interprété comme le groupe des symétries d'un triangle équilatéral.
Le théorème de Cayley prévoit que tout groupe fini (pas nécessairement abélien) peut être exprimée comme un sous-groupe d'un groupe symétrique S N.
La théorie des groupes primaire
La théorie des groupes primaire concerne les faits de base qui détiennent pour tous les groupes. Par exemple:
- Vous pouvez effectuer la division en groupes; ce est-donné les éléments A et B du groupe G, il ya exactement une solution en x G à la équation x * a = b et exactement une solution G y dans l'équation y = a * b. En fait, la droite, respectivement gauche multiplication de l'équation par un -1 donne la solution x = b * -1 respectivement y = a * b -1.
- (chaussettes et chaussures) L'inverse d'un produit est le produit des inverses dans l'ordre inverse: (a * b) -1 = b * -1 -1.
- Preuve: Nous allons démontrer que (a * b) * (b * -1 -1) = e, qui, comme mentionné ci-dessus suffit de prouver que b * -1 -1 est l'inverse de a * b.
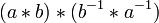
= 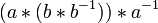
(Associativité) = 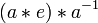
(Définition de inverse) = 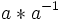
(Définition de l'élément neutre) = 
(Définition de inverse)
Construire de nouveaux groupes de celles données
Outre les sous-groupes et groupes quotients ya deux façons de base de la construction de nouveaux groupes de celles indiquées. D'autres techniques de manipulation comprennent:
- Produit direct: Si (G, *) et (H, •) sont des groupes, l'ensemble G × H avec l'opération (g 1, 1 h) (g 2, 2 h) = (1 g * g 2, • h 1 h 2) est un groupe. Le produit direct peut également être défini avec un nombre quelconque de termes, finis ou infinis, en utilisant le Produit cartésien et de définir le fonctionnement coordonnent-sage.
- Produit semi-direct: Si N et H sont des groupes et φ: H → Aut (N) est un homomorphisme de groupes, puis le produit semi-direct de N et H par rapport à φ est le groupe (N x H, *), avec * défini comme
- (N 1, h 1) * (n 2, h 2) = (n φ 1 (1 h) (n 2), h 1 h 2)
- Direct somme externe: La somme externe directe d'une famille de groupes est le sous-groupe du produit constitué par des éléments qui ont un nombre fini de coordonnées non-identité. Si la famille est la somme directe finie et le produit sont équivalentes.
Généralisations
| structures de groupe comme | |||||
| Totalité * | Associativité | Identité | Inverses | Commutativité | |
|---|---|---|---|---|---|
| Magma | Oui | Aucun | Aucun | Aucun | Aucun |
| Semigroup | Oui | Oui | Aucun | Aucun | Aucun |
| Monoid | Oui | Oui | Oui | Aucun | Aucun |
| Groupe | Oui | Oui | Oui | Oui | Aucun |
| Groupe abélien | Oui | Oui | Oui | Oui | Oui |
| Boucle | Oui | Aucun | Oui | Oui | Aucun |
| Quasigroupe | Oui | Aucun | Aucun | Oui | Aucun |
| Groupoïde | Aucun | Oui | Oui | Oui | Aucun |
| Catégorie | Aucun | Oui | Oui | Aucun | Aucun |
| Semicategory | Aucun | Oui | Aucun | Aucun | Aucun |
| * Fermeture, qui est utilisé dans de nombreuses sources pour définir les structures des groupes comme, est un axiome équivalent à la totalité, bien défini différemment. | |||||
En algèbre abstraite , des structures plus générales se posent en assouplissant certaines des axiomes définissant un groupe.
- Éliminer l'exigence que chaque élément possède un inverse, la structure algébrique résultant est appelé une monoïde.
- Un monoïde sans identité est appelé semi-groupe.
- Alternativement, assouplissement de l'exigence que l'opération soit associative , tout en exigeant la possibilité de division , la structure algébrique résultant est un boucle.
- Une boucle sans identité est appelé quasigroupe.
- Enfin, laisser tomber tous les axiomes de la relation binaire, la structure algébrique résultant est appelé une magma.
Groupoïdes, qui sont semblables à des groupes, sauf que la composition a * b ne doit pas être définie pour tout a et b, se pose dans l'étude des types plus complexes de symétries, souvent dans des structures topologiques et analytiques. Groupoïdes, à leur tour, sont de sortes spéciales catégories.
Supergroupes et Algèbres de Hopf sont autres généralisations, et sont donc tas.
Groupes abéliens forment le prototype pour le concept d'un catégorie abélienne, qui a des applications à des espaces vectoriels et au-delà.
Lois de groupe formelles sont certains séries formelles qui ont des propriétés un peu comme une exploitation de groupe.
En géométrie différentielle , la géométrie algébrique et la topologie , la notion de groupe est spécialisé pour inclure des groupes avec une structure supplémentaire. groupes de Lie, groupes algébriques et groupes topologiques sont des exemples de grouper des objets: structures des groupes comme assis dans un catégorie autre que la catégorie ordinaire des ensembles.