
Tesseract
Saviez-vous ...
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.
| Tesseract (8 cellules) 4-cube | |
|---|---|
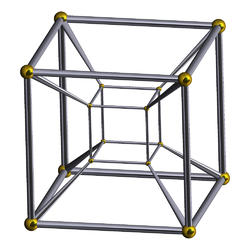 Diagramme de Schlegel | |
| Type | Polychoron régulière |
| Famille | hypercube |
| Cellules | 8 ( 4.4.4 ) |
| Visages | 24 {4} |
| Bords | 32 |
| Sommets | 16 |
| Figure de sommet | ( 3.3.3 ) |
| Symboles Schläfli | {4,3,3} {4,3} x {} {4} x {4} {4} {x} x {} X {} {} {} x {x} |
| Diagrammes de Coxeter-Dynkin | |
| Groupe Symétrie | B 4, [3,3,4] |
| Double | 16 cellules |
| Propriétés | convexe |
En géométrie , le Tesseract, également appelé 8-cellule ou octachoron, est le analogique à quatre dimensions du cube , qui est à son tour les trois dimensions de l'analogique carré . Le Tesseract est au cube comme le cube est à la place ; ou, plus formellement, le tesseract peut être décrit comme un convexe 4-polytope régulier dont la frontière se compose de huit cubique cellules.
Une généralisation du cube à trois dimensions supérieures est appelé un " hypercube »,« n-cube »ou« mesure polytope ". Le Tesseract est l'hypercube en quatre dimensions ou 4-cube.

Selon le Oxford English Dictionary, le mot a été inventé Tesseract et le premier utilisé en 1888 par Charles Howard Hinton dans son livre Une nouvelle ère de la pensée, de la grecque "τέσσερεις ακτίνες" ("quatre rayons»), se référant aux quatre lignes de chaque sommet à d'autres sommets. Certaines personnes ont demandé la même figure un «tetracube", et aussi tout simplement un «hypercube» (même si un hypercube peuvent être de ne importe quelle dimension).
Géométrie
Le tesseract peut être construite dans un certain nombre de façons différentes. Comme un polytope régulier construit par trois cubes pliées ensemble autour de chaque bord, elle a Symbole Schläfli {4,3,3}. Construit comme un 4D Hyperprism fait de deux cubes parallèles, il peut être désigné comme un symbole Schläfli {4,3} composite x {}. Comme un Duoprisme, un Produit cartésien de deux carrés , il peut être appelé par un symbole composite Schläfli {4} x {4}.
Étant donné que chaque sommet d'un tesseract est adjacente à quatre côtés, le vertex figure du Tesseract est un habitué tétraèdre . Le double polytope du tesseract est appelé hexadecachoron, ou 16 cellules, avec le symbole Schläfli {3,3,4}.
Le Tesseract standard dans euclidienne 4-espace est donné comme le enveloppe convexe des points (± 1, ± 1, ± 1, ± 1). Autrement dit, il se compose de points:
Un Tesseract est délimitée par huit hyperplans (x i = ± 1). Chaque paire de hyperplans non parallèles coupe pour former 24 faces carrées dans un tesseract. Trois cubes et trois places se croisent à chaque bord. Il ya quatre cubes, six places, et quatre bords réunis à chaque sommet. Dans l'ensemble, il se compose de huit cubes, 24 places, 32 arêtes et 16 sommets.
Projections à deux dimensions
La construction d'un hypercube peut être imaginé de la manière suivante:
- 1 dimensions: deux points A et B peuvent être connectés à une ligne, ce qui donne une nouvelle ligne AB.
- Deux dimensions: deux lignes parallèles AB et CD peuvent être reliés pour devenir un carré, avec des coins marquées comme étant ABCD.
- Trois dimensions: Deux carrés ABCD et EFGH parallèles peuvent être reliés pour devenir un cube, avec des angles marqués comme ABCDEFGH.
- Quatre dimensions: deux cubes parallèles ABCDEFGH IJKLMNOP et peut être relié à devenir un hypercube, avec des angles marqués comme ABCDEFGHIJKLMNOP.
Cette structure ne est pas facilement imaginé mais il est possible de projeter dans les espaces tesseracts trois ou deux dimensions. En outre, les projections sur le plan 2D deviennent plus instructif en réarrangeant les positions des sommets projetés. De cette manière, on peut obtenir des images qui ne reflètent plus les relations spatiales au sein du tesseract, mais qui illustrent la structure de connexion des sommets, comme dans les exemples suivants:
Un Tesseract est en principe obtenu par la combinaison de deux cubes. Le schéma est similaire à la construction d'un cube de deux carrés: juxtaposer deux copies du cube de moindre dimension et de connecter les sommets correspondants. Chaque bord d'un tesseract est de la même longueur. Une multitude de cubes qui sont bien reliées entre elles. Les sommets du tesseract par rapport à la distance le long des bords, par rapport au point bas. Ce point de vue est d'un intérêt pour l'utilisation de tesseracts de base à un topologie de réseau pour relier plusieurs processeurs dans calcul parallèle: la distance entre deux nœuds est au plus quatre et il ya de nombreux chemins différents pour permettre masse d'équilibrage.
Sont également Tesseracts graphes bipartites, tout comme un chemin, carré, cube et arbre sont.
Projections à trois dimensions
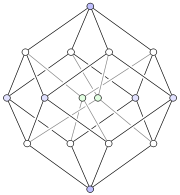
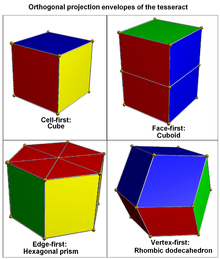
La première cellule parallèle projection du tesseract dans l'espace trois dimensions a une forme cubique enveloppe. Les cellules les plus proches et les plus éloignés sont projetées sur le cube, et les six cellules restantes sont projetées sur les six faces carrées du cube.
La projection parallèle tête la première de la Tesseract dans l'espace en 3 dimensions a une enveloppe cubique. Deux paires de cellules de projeter les moitiés supérieure et inférieure de cette enveloppe, et les quatre cellules restantes font saillie sur les faces latérales.
La projection parallèle de bord de la première tesseract dans l'espace à 3 dimensions dans une enveloppe a la forme d'un prisme hexagonal. Six cellules projettent sur prismes rhombiques, qui sont énoncées dans le prisme hexagonal d'une manière analogue à la façon dont les faces du projet de cube 3D SUR DES six losanges dans une enveloppe hexagonale sous projection de vertex-première. Les deux cellules restantes projettent sur les bases du prisme.
La projection parallèle-premier sommet de la tesseract dans l'espace à 3 dimensions a un enveloppe dodécaèdre rhombique. Il ya exactement deux façons de décomposer un dodécaèdre rhombique dans quatre congruent parallélépipèdes, donnant un total de huit parallélépipèdes possibles. Les images des cellules de Tesseract sous cette projection sont précisément ces huit parallélépipèdes. Cette projection est aussi celui avec le volume maximal.
Déplier le tesseract
Le Tesseract peut être déplié en huit cubes, tout comme le cube peut être déplié en six carrés. Un déroulement d'un polytope est appelé net. Il ya 261 filets distincts du tesseract. Les déploiements de la tesseract peuvent être comptés par la cartographie des filets aux arbres appariés (un un arbre avec appariement parfait dans son complément).
Tesseracts dans la culture populaire
Livres / print
- Le roman de Madeline L'Engle A Wrinkle in Time utilise tesseracts comme un moyen pour Meg Murry et ses compagnons de voyager vers d'autres planètes et les dimensions, mais la description correspond davantage à un trou de ver.
- Carl Sagan décrit le tesseract en détail en utilisant des termes simples dans Cosmos, l'épisode 10.
- En Le roman de Edwin A. Abbott Flatland, 1884, un hypercube est imaginé par le narrateur.
- Robert A. Heinlein mentionné hypercubes dans au moins trois de ses histoires de science-fiction. En «-Et Il a construit une Crooked Maison-" (1940), il a décrit une maison construite comme un filet (c.-à-un déploiement des cellules dans l'espace en trois dimensions) d'un tesseract. Il se est effondré, devenant un véritable tesseract quatre dimensions. 1963 roman de Heinlein Glory Road inclus l'foldbox, une caisse d'emballage hyperdimensionnel qui était plus grand à l'intérieur qu'à l'extérieur.
- Hypercubes et toutes sortes d'espace et de structures multi-dimensionnelle étoiles en bonne place dans de nombreux livres par Rudy Rucker.
- Un hypercube est utilisé comme principal deus ex machina de Le livre de Robert J. Sawyer Affacturage humanité, apparaissant même sur sa couverture en Amérique du Nord.
- Le roman de Piers Anthony Cube Route dispose également d'un tesseract.
- Le deuxième livre de Alex Garland est appelé "Tesseract: a novel".
- Le DC Comics croisé DC One Million montré une Terre future dans laquelle les villes occupées zones extradimensionnels appelés tesseracts, laissant la surface de la planète intacte. Une technologie similaire a été utilisée pour Superman actuelle de l ' Forteresse de Solitude, et a été utilisé comme espace de stockage dans le siège de l'incarnation originale (pré- Zero Hour) de la Légion des Super-Héros.
- Sci-Fi Fantasy Ian Irvine 'tétrarque «Livre deux du' The Well of Echoes Quartet».
- David Lubar de «Sleeping Freshmen ne mentent jamais». Tesseract signifiant «spirale dans une autre dimension."
- Bref classique de Lewis Padgett, ' Caractéristiques des borogoves Enmîmés sont deux enfants qui construisent un tesseract utilisant les informations de l'avenir. Ils disparaissent finalement dans une autre dimension.
- Umberto Eco référence dans tesseracts Pendule de Foucault
Arts visuels
- La peinture Crucifixion (Corpus Hypercubus), par Salvador Dalí, 1954, représente le crucifié Jésus sur le net d'un hypercube. Il est présenté à la Metropolitan Museum of Art de New York, États-Unis .
Télévision et le cinéma
- Le programme de télévision Andromeda fait usage de générateurs de Tesseract comme un appareil de complot. Elles sont principalement destinées à manipuler l'espace (aussi appelé déphasage) mais provoquent souvent des problèmes avec le temps ainsi.
- Un caractère dans le programme de télévision Numb3rs montre un modèle d'un tesseract dans l'épisode Rampage deuxième saison, lors d'une discussion de l'utilisation d'un point de vue quatre dimensions pour analyser un événement.
- Le programme TV Les Secrets de Blake Holsey a un épisode où le campus de l'école se transforme en un hypercube auto-pliage.
- Le film Cube 2 se concentre sur huit étrangers piégés à l'intérieur d'un filet de cubes connectés ou peut-être une sorte de Tesseract qui décale dans le sens des huit inconnus mouvements dans toutes les directions, faisant un continuum apparemment sans fin de cubes singuliers.
- Le film The Last Mimzy mentionne tesseracts dans une liste d'autres formes géométriques lorsque les enfants rêvent sur le pont à travers l'univers, comme le fait la courte histoire sur laquelle il est basé, ' Tout smouales étaient les Borogoves »(ci-dessus). Cela peut aussi être en hommage à A Wrinkle in Time .
Entreprise
- Tesseract Books était un éditeur de premier plan de livres canadiens de science-fiction. La société est maintenant une empreinte de Hadès Publishing Inc.
Jeux Vidéo
- Starflight comprenait un tesseract comme un artefact qui pourrait être trouvé en explorant la surface des planètes.
Jeux
- Un tesseract constitue la base de la fantaisie Advanced Dungeons & Dragons Module Hut de Baba Yaga, paru dans un numéro au début de Dragon Magazine, avec le tesseract existante que l'intérieur de la cabane titulaire.

