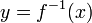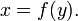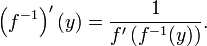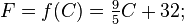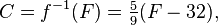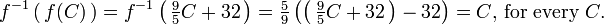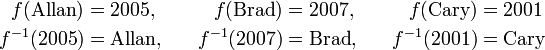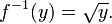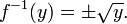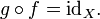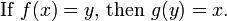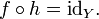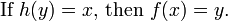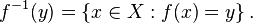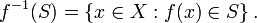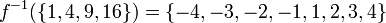Función inversa
Antecedentes
SOS Children, una organización benéfica educación , organizó esta selección. Ver http://www.soschildren.org/sponsor-a-child para averiguar sobre el apadrinamiento de niños.
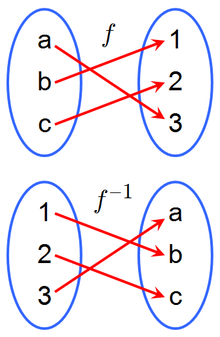
En matemáticas , una función inversa es una función que deshace otra función: Si un x entrada en la función f produce una salida y, a continuación, poner y en la función inversa g produce la salida x, y viceversa. es decir, f (x) = y, y g (y) = x. Más directamente, g (f (x)) = x, es decir, g (x) compuestos con f (x) x deja sin cambios.
Una función f que tiene una inversa se llama invertible; la función inversa es entonces determinada únicamente por f y se denota por f -1 (lectura inversa f, que no debe confundirse con la exponenciación ).
Definiciones
La palabra inverso se relaciona con la palabra invertido significa revertir, gire al revés, hacer lo contrario.
| Buscar inversa en Wikcionario, el diccionario libre. |

En lugar de considerar las inversas de las entradas y salidas individuales, se puede pensar en la función como el envío de todo el conjunto de entradas, la de dominio, a un conjunto de salidas, las gama. Sea f una función cuyo dominio es el conjunto X, y cuyo rango es el conjunto Y. Entonces f es invertible si existe una función g con dominio Y y gama X, con la característica:
Si f es invertible, la función g es único; en otras palabras, no es exactamente una función g satisfacer esta propiedad (ni más ni menos). Esa función g se llama entonces la inversa de f, y por lo general denota como f -1.
Dicho de otra manera, una función es invertible si y sólo si su relación inversa es una función en el rango Y, en cuyo caso la relación inversa es la función inversa.
No todas las funciones tienen un inverso. Por esta regla sea aplicable, cada elemento y ∈ Y debe corresponder a no más de un x ∈ X; una función f con esta propiedad se llama uno a uno, o la información de preservación, o un inyección.
Operaciones inversas que conducen a la inversa funciones: Ejemplo
Operaciones inversas son lo contrario de las funciones de variación directa. Función de la variación directa se basan en la multiplicación; y = kx. La operación inversa de la multiplicación es la división y una función de variación inversa es y = k / x.
Ejemplo: cuadratura y funciones de las raíces cuadradas
La función f (x) = x 2 puede o no puede ser invertible, en función del dominio.
Si el dominio es los números reales, a continuación, cada elemento en Y correspondería a dos elementos diferentes en X (± x), y por lo tanto f no sería invertible. Más precisamente, la cuadrada de x no es invertible, ya que es imposible deducir de su salida la señal de su entrada. Tal función se llama no inyectiva o información perdida. Tenga en cuenta que ni la raíz cuadrada ni la raíz cuadrada principal función es la inversa de x 2 debido a que el primero no es rendimientos de un solo valor, y la segunda - x cuando x es negativo.
Si el dominio se compone de los números no negativos, entonces la función es inyectiva y invertible.
Inversas en matemáticas superiores
La definición dada anteriormente es adoptado comúnmente en la teoría de conjuntos y cálculo . En matemáticas superiores, la notación
significa "f es una serie de elementos de correlación de funciones de un conjunto X a elementos de un conjunto Y". La fuente, X, se llama el dominio de f, y el objetivo, Y, se llama la codominio. El codominio contiene el rango de f como un subconjunto , y se considera parte de la definición de f.
Al usar codomains, la inversa de una función f: X → Y se requiere que tengan dominio Y y codominio X. Para la inversa a definirse en todos Y, cada elemento de Y debe estar en el rango de la función f. Una función con esta propiedad se llama a una o surjection. Por lo tanto, una función con un codomain es invertible si y sólo si es tanto inyectiva (uno-a-uno) y sobreyectiva (a). Tal función se llama uno-a-uno o una biyección, y tiene la propiedad de que cada elemento y ∈ Y corresponde a exactamente un elemento x ∈ X.
Inversas y composición
Si f es una función invertible con el dominio X y el rango Y, a continuación,
Esta declaración es equivalente a la primera de las definiciones de la inversa antes indicados, y se vuelve equivalente a la segunda definición si Y coincide con el codomain de f. Uso de la composición de funciones se puede reescribir esta declaración como sigue:
donde id es la X función identidad en el conjunto X; es decir, la función que deja X sin cambios. En la teoría de categorías, esta declaración se utiliza como la definición de una inversa morfismo.
Si pensamos en la composición como una especie de multiplicación de funciones, esta identidad dice que la inversa de una función es análoga a una inverso multiplicativo. Esto explica el origen de la notación f -1.
Nota sobre la notación
La notación superíndice para inversas a veces se puede confundir con otros usos de superíndices, especialmente cuando se trata de trigonométricas y funciones hiperbólicas. Para evitar esta confusión, las notaciones f [-1] o con el "-1" por encima de la f son utilizadas habitualmente.
Es importante darse cuenta de que f -1 (x) no es el mismo que f (x) -1. En f -1 (x), el exponente "-1" no es un exponente . Una notación similar se utiliza para funciones iteradas. Por ejemplo, f 2 denota dos iteraciones de la función f; si f (x) = x 2 - 1, entonces f 2 (x) = f (f (x)) = f (x 2 - 1) = (x 2 - 1) 2 - 1, lo que simplifica al x 4 - 2 x 2. En símbolos:
En cálculo, f (n), con paréntesis, indica la enésima derivada de una función f. Por ejemplo:
En trigonometría , por razones históricas, el pecado 2 x por lo general significa que sean la plaza del pecado x:
Sin embargo, los pecados expresión -1 x lo general no representa el inverso multiplicativo de pecar x, pero la inversa de la función seno aplicado a x (en realidad un inverso parcial , véase más adelante). Para evitar confusiones, una función trigonométrica inversa se indica a menudo por el prefijo "arco". Por ejemplo, la inversa de la función seno se denomina normalmente el función arco seno, escrito como arcsin, que es, como el pecado, convencionalmente denotado en tipo romano y no en cursiva (nota que las bibliotecas de software de funciones matemáticas a menudo utilizar el nombre asin):
La función (sen x) -1 es el inverso multiplicativo al seno, y se llama la cosecante . Por lo general se denota csc x:
Funciones hiperbólicas comportan de manera similar, utilizando el prefijo "ar", como en arsinh para la función inversa de Sinh, y csch x para el inverso multiplicativo de senh x.
Propiedades
Unicidad
Si existe una función inversa de una función f dada, es único: debe ser el relación inversa.
Simetría
Hay una simetría entre una función y su inversa. Específicamente, si f es una función invertible con el dominio X y el rango Y, a continuación, su inversa f -1 tiene dominio de Y y X gama, y la inversa de f -1 es la función original f. En símbolos, por f una función con dominio X y rango Y, yg una función con dominio Y y gama X:
Esto se deduce de la conexión entre la función inversa y relación inversa, porque inversión de las relaciones es una involución.
Esta declaración es una consecuencia obvia de la deducción que para f sea invertible debe ser inyectiva (primera definición de la inversa) o biyectiva (segunda definición). La propiedad de simetría se puede expresar de forma concisa por la siguiente fórmula:
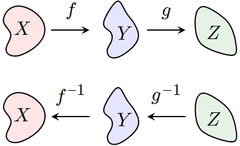
La inversa de una composición de funciones está dada por la fórmula
Observe que el orden de g y f se han invertido; para deshacer f seguido de g, primero tenemos que deshacer g y luego deshacer f.
Por ejemplo, sea f (x) = x 3 y sea g (x) = x + 5 Entonces la composición g o f es la función que primero se multiplica por tres y luego añade cinco.:
Para revertir este proceso, primero tenemos que restar cinco, y luego dividir por tres:
Esta es la composición (f -1 o g -1) (y).
Auto-inversas
Si X es un conjunto, entonces el función identidad sobre X es su propio inverso:
Más en general, una función f: X → X es igual a su propia inversa si y sólo si la composición f o f es igual a X ID. Tal función se llama una involución.
Inversas en el cálculo
Single-variable de cálculo se refiere principalmente a las funciones que se asignan números reales a los números reales. Tales funciones se definen a menudo a través de fórmulas , tales como:
Una función f de los números reales a los números reales posee una inversa con tal de que es uno-a-uno, es decir, mientras la gráfica de y = f (x) tiene, para cada posible valor de y sólo un correspondiente valor x , y pasa así la prueba de la línea horizontal.
La siguiente tabla muestra varias funciones estándar y sus inversas:
La función f (x) F Inverse -1 (y) Notas x + a y - una a - x a - y mx a / m m ≠ 0 1 / x 1 / y x, y ≠ 0 x 2 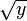
x, y ≥ 0 sólo x 3 ![\ Sqrt [3] {y}](../../images/2472/247204.png)
ninguna restricción en x e y x p y 1 / p (es decir, ![\ Sqrt [p] {y}](../../images/2472/247205.png) )
) x, y ≥ 0, en general, p ≠ 0 e x ln y y> 0 una x ingrese una y y> 0 y> 0 funciones trigonométricas funciones trigonométricas inversas diversas restricciones (ver tabla abajo)
Fórmula para la inversa
Un enfoque para encontrar una fórmula para f -1, si existe, es resolver la ecuación y = f (x) para x. Por ejemplo, si f es la función de
entonces tenemos que resolver la ecuación y = (2 x + 8) 3 para x:
Así, la función inversa f -1 viene dado por la fórmula
A veces, la inversa de una función no puede ser expresado por una fórmula con un número finito de términos. Por ejemplo, si f es la función de
entonces f es uno-a-uno, y por lo tanto posee una función inversa f -1. La fórmula para este inversa tiene un número infinito de términos:
Gráfico de la inversa
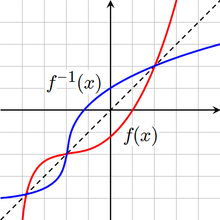
Si f y f -1 son inversas, entonces la gráfica de la función de
es la misma que la gráfica de la ecuación
Esto es idéntico a la ecuación y = f (x) que define la gráfica de f, excepto que las funciones de X e Y se han invertido. Así, el gráfico de f -1 puede obtenerse a partir de la gráfica de f al cambiar las posiciones de los ejes x e y. Esto es equivalente a lo que refleja el gráfico a la recta y = x.
Inversas y derivados
La función continua f es uno-a-uno (y por lo tanto invertible) si y sólo si es ya sea estrictamente aumentando o disminuyendo (sin locales máximos o mínimos). Por ejemplo, la función de
es invertible, ya que el derivado de f '(x) = 3 x 2 + 1 es siempre positivo.
Si la función f es diferenciable, entonces la inversa f -1 será diferenciable siempre que f '(x) ≠ 0. El derivado de la inversa es dada por el función inversa teorema:
Si fijamos x = f -1 (y), entonces la fórmula anterior se puede escribir
Este resultado se deduce de la regla de la cadena (ver el artículo sobre Derivada de la función inversa).
El teorema de la función inversa se puede generalizar a funciones de varias variables. Específicamente, una función diferenciable f: R → R n n es invertible en un entorno de un punto p, siempre y cuando la Jacobiano matriz de f en p es invertible. En este caso, el Jacobiano de f -1 en f (p) es la matriz inversa del Jacobiano de f en p.
Ejemplos del mundo real
Por ejemplo, sea f la función que convierte una temperatura en grados Celsius a una temperatura en grados Fahrenheit:
entonces su función inversa convierte grados Fahrenheit a grados Celsius:
desde
O supongamos que f asigna a cada niño en una familia de su año de nacimiento. Una función inversa sería de salida que niño nació en un año determinado. Sin embargo, si la familia tiene gemelos (o trillizos), la salida no puede ser conocido cuando la entrada es el año de nacimiento común. Además, si se le da un año en el que ningún niño nace entonces un niño no puede ser nombrado. Pero si cada niño nacido en un año distinto, y si restringimos la atención a los tres años en los que ha nacido un niño, entonces sí tenemos una función inversa. Por ejemplo,
Las generalizaciones
Inversos parciales
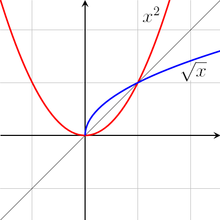
Incluso si una función f no es uno-a-uno, puede ser posible definir un inverso parcial de f por restringir el dominio. Por ejemplo, la función de
no es uno-a-uno, ya que x = 2 (- x) 2. Sin embargo, la función se convierte en uno-a-uno si se restringe el dominio x ≥ 0, en cuyo caso
(Si nos restringimos lugar al dominio x ≤ 0, entonces la inversa es el negativo de la raíz cuadrada de y.) Por otra parte, no hay necesidad de restringir el dominio si nos contentamos con la inversa de ser un función de varios valores:
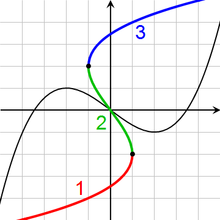
A veces esto inversa de varios valores se llama la inversa llena de f, y las porciones (como √ x y -√ x) se llaman ramas. La rama más importante de una función de varios valores (por ejemplo, la raíz cuadrada positiva) se denomina la rama principal, y su valor en y se llama el valor principal de f -1 (y).
Para una función continua en la línea real, se requiere una rama entre cada par de extremos locales. Por ejemplo, la inversa de una función cúbica, con un máximo local y mínimo local tiene tres ramas (ver la imagen a la derecha).
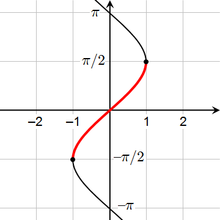
Estas consideraciones son especialmente importantes para la definición de las inversas de las funciones trigonométricas . Por ejemplo, el función seno no es uno-a-uno, ya
Para cada x reales (y más generalmente sin (x + 2π n) = sen (x) para cada número entero n). Sin embargo, el seno es uno-a-uno en el intervalo [- π / 2, π / 2], y la inversa parcial correspondiente se llama el arcoseno. Esta es considerada la rama principal del seno inverso, por lo que el valor principal de la inversa del seno está siempre entre - π / 2 y π / 2. La siguiente tabla describe la rama principal de cada función trigonométrica inversa:
función Gama de costumbre valor principal sin -1 - Π / 2 ≤ sin -1 (x) ≤ π / 2 cos -1 0 ≤ cos -1 (x) ≤ π tan -1 - Π / 2 <tan -1 (x) <π / 2 cuna -1 0 <cuna -1 (x) <π seg -1 0 ≤ s-1 (x) ≤ π csc -1 - Π / 2 ≤ -1 csc (x) ≤ π / 2
Inversas izquierda y derecha
Si f: X → Y, una inversa izquierda para f (o retracción de f) es una función g: Y → X tal que
Es decir, la función g satisface la regla
Por lo tanto, g debe ser igual a la inversa de f en el rango de f, pero puede tomar cualquier valor para los elementos de Y no en el rango. Una función f con una inversa izquierda es necesariamente inyectiva. En la matemática clásica, toda función f inyectiva tiene necesariamente una inversa por la izquierda; sin embargo, esto puede fallar en matemáticas constructivas. Por ejemplo, una inversa izquierda de la inclusión {0,1} → R de los dos elementos fijado en los reales viola indescomponibilidad dando un la retracción de la línea real para el conjunto {0,1}.
Un inversa derecha para f (o la sección de f) es una función h: Y → X tal que
Es decir, la función h satisface la regla
Por lo tanto, h (y) puede ser cualquiera de los elementos de X que se asignan a y bajo f. Una función f tiene una inversa derecha si y sólo si es sobreyectiva (aunque la construcción de una inversa como en general requiere la axioma de elección).
Un inversa que es a la vez a la izquierda y derecha inversa deben ser únicos. Del mismo modo, si g es una inversa izquierda de f, entonces g puede o no ser una inversa derecha de f; y si g es una inversa derecha de f, entonces g no es necesariamente una inversa izquierda para f. Por ejemplo sea f: R → [0, ∞) denota el mapa cuadratura, tal que f (x) = x 2 para todo x en R, y sea g: [0, ∞) → R denotar el mapa raíz cuadrada, tal que g (x) = √x para todos x≥0. Entonces f (g (x)) = x para todo x en [0, ∞); es decir, g es un inverso derecho a f. Sin embargo, g no es una inversa izquierda a F, ya que, por ejemplo, g (f (-1)) = 1 ≠ -1.
Preimages
Si f: X → Y es una función cualquiera (no necesariamente invertible), la imagen inversa (o imagen inversa) de un elemento y ∈ Y es el conjunto de todos los elementos de X que se correlacionan con y:
La preimagen de y puede ser pensado como la imagen de y bajo la (varios valores) inverso total de la función f.
Del mismo modo, si S es cualquier subconjunto de Y, la imagen inversa de S es el conjunto de todos los elementos de X que se asignan a S:
Por ejemplo, tener una función f: R → R, donde f: x ↦ x 2. Esta función no es invertible por las razones discutidas anteriormente . Sin embargo preimages pueden definirse para subconjuntos de la codominio:
La preimagen de un solo elemento y ∈ Y - una singleton conjunto {y} - a veces se llama la fibra de y. Cuando Y es el conjunto de números reales, es común referirse a f -1 (y) como una establecer el nivel.
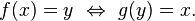
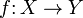

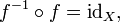

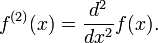
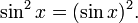
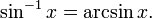
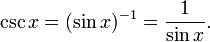
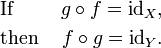
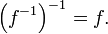
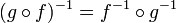
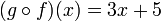

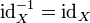
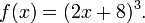
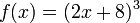
![\ Begin {align} y & = (2x + 8) ^ 3 \\ \ sqrt [3] {y} y = 2x + 8 \\ \ sqrt [3] {y} - 8 y = 2x \\ \ dfrac { \ sqrt [3] {y} - 8} {2} y = x. \ End {align}](../../images/2472/247207.png)
![f ^ {- 1} (y) = \ dfrac {\ sqrt [3] {y} - 8} {2}. \, \!](../../images/2472/247208.png)
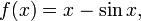
![f ^ {- 1} (y) = \ displaystyle \ sum_ {n = 1} ^ {\ infty} {! \ frac {y ^ {\ frac {n} {3}}} {n}} \ lim_ {\ theta \ a 0} \ left (\ frac {\ mathrm {d} ^ {\, n-1}} {\ mathrm {d} \ theta ^ {\, n-1}} \ left (\ frac {\ theta } {\ sqrt [3] {\ theta - \ sin (\ theta)}} ^ n \ right) \ right)](../../images/2472/247210.png)