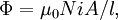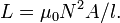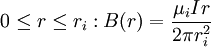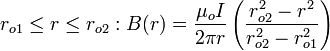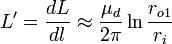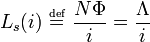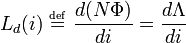Inductancia
Acerca de este escuelas selección Wikipedia
Los artículos de esta selección escuelas se han organizado por tema currículo gracias a voluntarios SOS. Haga clic aquí para obtener información sobre el apadrinamiento de niños.
| Electromagnetismo |
|---|
 |
Electrostática
|
Magnetoestática
|
Electrodinámica
|
Red eléctrica
|
Formulación covariante Tensor electromagnético ( tensor de tensión-energía)
|
En el electromagnetismo y la electrónica , la inductancia es propiedad de una conductor por el cual un cambio en corriente en el conductor "induce" (crea) una voltaje ( fuerza electromotriz), tanto en el propio conductor (autoinducción) y en ningún conductores cercanos (inductancia mutua). Este efecto se deriva de dos observaciones fundamentales de la física: En primer lugar, que una corriente constante crea un campo magnético constante ( De la ley Oersted) y en segundo lugar, que un campo magnético variable en el tiempo induce una tensión en un conductor en las inmediaciones ( Ley de Faraday). Desde La ley de Lenz, en una circuito eléctrico, una corriente eléctrica cambiante a través de un circuito que tiene inductancia induce una tensión proporcional que se opone al cambio en la corriente (autoinductancia). El campo variable en este circuito también puede inducir una fem en un circuito (inductancia mutua) vecino.
El término "inductancia" fue acuñado por Oliver Heaviside en febrero de 1886. Se acostumbra a utilizar el símbolo L para inductancia, en honor del físico Heinrich Lenz. En el Sistema SI la unidad de inductancia es el henry, llamado así en honor al científico que descubrió la inductancia, Joseph Henry.
Para añadir inductancia de un circuito, eléctrica o componentes electrónicos llamados se utilizan inductores, que consiste típicamente en rollos de alambre para concentrar el campo magnético y para que el campo magnético se integran en el circuito más de una vez.
La relación entre la autoinductancia L de un circuito eléctrico en henrios, el voltaje y la corriente es
donde v denota la tensión en voltios y i la corriente en amperios. El voltaje a través de un inductor es igual al producto de su inductancia y la tasa de tiempo de cambio de la corriente a través de él.
Todos los circuitos prácticos tienen alguna inductancia, que puede proporcionar efectos beneficiosos o perjudiciales. En un inductancia de circuito sintonizado se utiliza para proporcionar un circuito de frecuencia selectiva. Inductores prácticos pueden ser utilizados para proporcionar la filtración o el almacenamiento de energía en un sistema. La inductancia de una línea de transmisión es una de las propiedades que determina su impedancia característica; el equilibrio de la inductancia y capacitancia de los cables es importante para la distorsión de libre telegrafía y telefonía. La inductancia de largas líneas de transmisión de energía limita la alimentación de CA que se pueden enviar a través de ellos. Circuitos sensibles tales como micrófono y cables de la red de ordenadores pueden utilizar construcciones de cable especiales para limitar la inductancia mutua entre los circuitos de señal.
En el análisis de circuitos
La generalización para el caso de circuitos eléctricos con corrientes de K i M y tensiones v m lee
Inductancia aquí hay una matriz simétrica. La diagonal coeficientes L m, m son llamados coeficientes de autoinducción, los elementos fuera de la diagonal son llamados coeficientes de inductancia mutua. Los coeficientes de inductancia son constantes mientras no material magnetizable con características no lineales está involucrado. Esto es una consecuencia directa de la linealidad de las ecuaciones de Maxwell en los campos y la densidad de corriente. Los coeficientes de la inductancia se convierten en funciones de las corrientes en el caso no lineal, ver la inductancia no lineal .
Derivación de la ley de Faraday de la inductancia
Las ecuaciones de inductancia anteriores son consecuencia de las ecuaciones de Maxwell . No es una derivación directa en el caso importante de circuitos eléctricos que consisten en alambres delgados.
Considere un sistema de bucles de alambre K, cada uno con una o varias vueltas de alambre. La enlace de flujo de bucle m está dado por
Aquí N m denota el número de vueltas en bucle m, Φ m el flujo magnético a través de este bucle, y L m, n son algunas constantes. Esta ecuación se sigue de La ley de Ampere - campos y flujos magnéticos son funciones lineales de las corrientes. Por Ley de Faraday tenemos
donde v m denota la tensión inducida en el circuito m. Esto concuerda con la definición de la inductancia por encima de si los coeficientes L m, n se identifican con los coeficientes de inductancia. Debido a las corrientes totales N n i n contribuyen a Φ m también se deduce que L m, n es proporcional al producto de vueltas N m N n.
Inductancia y la energía del campo magnético
Multiplicando la ecuación para v m anteriormente con i m dt y sumando sobre m da la energía transferida al sistema en el intervalo de tiempo dt,
Este debe estar de acuerdo con el cambio de la energía magnética W campo causado por las corrientes. La condición de integrabilidad
requiere L m, n = L n, m. La matriz de inductancia L m, n por lo tanto es simétrica. La integral de la transferencia de energía es la energía del campo magnético como una función de las corrientes,
Esta ecuación también es una consecuencia directa de la linealidad de las ecuaciones de Maxwell. Es útil para asociar el cambio corrientes eléctricas con una acumulación o disminución de la energía del campo magnético. La transferencia de energía correspondiente requiere o genera un voltaje. Una analogía mecánica en el caso K = 1 con la energía del campo magnético (1/2) Li 2 es un cuerpo con masa M, velocidad u y la energía cinética (1/2) Mu 2. La velocidad de cambio de la velocidad (actual) multiplicado por la masa (inductancia) requiere o genera una fuerza (tensión eléctrica).
Inductores acoplados

Inductancia mutua se produce cuando el cambio en la corriente en un inductor induce un voltaje en otro inductor cerca. Es importante que el mecanismo por el cual transformadores de trabajo, pero también pueden causar el acoplamiento no deseado entre los conductores en un circuito.
La inductancia mutua, M, es también una medida del acoplamiento entre dos inductores. La inductancia mutua por el circuito en el circuito i j viene dada por la integral doble Fórmula Neumann, consulte técnicas de cálculo
La inductancia mutua también tiene la relación:
donde
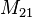 es la inductancia mutua, y el subíndice especifica la relación de la tensión inducida en la bobina 2 debido a la corriente en la bobina 1.
es la inductancia mutua, y el subíndice especifica la relación de la tensión inducida en la bobina 2 debido a la corriente en la bobina 1. - N 1 es el número de vueltas en la bobina 1,
- N 2 es el número de vueltas en la bobina 2,
- P 21 es el permeabilidad del espacio ocupado por el flujo.
La inductancia mutua también tiene una relación con el coeficiente de acoplamiento. El coeficiente de acoplamiento es siempre entre 1 y 0, y es una manera conveniente para especificar la relación entre una determinada orientación de inductores con inductancia arbitraria:
donde
- k es el coeficiente de acoplamiento y 0 ≤ k ≤ 1,
- L 1 es la inductancia de la primera bobina, y
- L 2 es la inductancia de la segunda bobina.
Una vez que la inductancia mutua, M, se determina a partir de este factor, que puede ser utilizado para predecir el comportamiento de un circuito:
donde
- V 1 es el voltaje a través del inductor de interés,
- L 1 es la inductancia del inductor de interés,
- d I 1 / d t es la derivada, con respecto al tiempo, de la corriente a través del inductor de interés,
- d I 2 / d t es la derivada, con respecto al tiempo, de la corriente a través del inductor que está acoplado a la primera inductor, y
- M es la inductancia mutua.
El signo menos surge debido a el sentido de la corriente I 2 se ha definido en el diagrama. Con las dos corrientes definidas entrar en los puntos de la señal de M será positivo.
Cuando un inductor está estrechamente acoplado a otro inductor a través de la inductancia mutua, tal como en una transformador, tensiones, corrientes, y el número de vueltas puede ser relacionados de la siguiente manera:
donde
- V s es el voltaje a través del inductor secundario,
- V p es el voltaje a través del inductor primario (el que está conectado a una fuente de energía),
- N s es el número de vueltas en la bobina secundaria, y
- N p es el número de vueltas en la bobina primaria.
Por el contrario la corriente:
donde
- I s es la corriente a través del inductor secundario,
- I p es la corriente a través del inductor primario (el que está conectado a una fuente de energía),
- N s es el número de vueltas en la bobina secundaria, y
- N p es el número de vueltas en la bobina primaria.
Tenga en cuenta que la potencia a través de un inductor es la misma que la potencia a través de la otra. También tenga en cuenta que estas ecuaciones no funcionan si ambos transformadores están obligados (con fuentes de energía).
Cuando cualquiera de los lados del transformador es una circuito sintonizado, la cantidad de inductancia mutua entre los dos devanados determina la forma de la curva de respuesta de frecuencia. Aunque no hay límites se definen, esto se refiere a menudo como loose-, criticidad, y el exceso de acoplamiento. Cuando dos circuitos sintonizados están débilmente acoplados a través de la inductancia mutua, el ancho de banda será estrecha. Como aumenta la cantidad de inductancia mutua, el ancho de banda continúa creciendo. Cuando la inductancia mutua se incrementa más allá de un punto crítico, el pico en la curva de respuesta comienza a caer, y la frecuencia central se atenúa más fuertemente que sus bandas laterales directas. Esto se conoce como sobreacoplamiento.
Las técnicas de cálculo
En el caso más general, la inductancia se puede calcular a partir de las ecuaciones de Maxwell. Muchos casos importantes se pueden resolver mediante simplificaciones. Cuando se consideran corrientes de alta frecuencia, con efecto de la piel, las densidades de corriente de superficie y el campo magnético se puede obtener resolviendo la ecuación de Laplace. Cuando los conductores son alambres delgados, autoinductancia todavía depende del radio del alambre y la distribución de la corriente en el alambre. Esta distribución de la corriente es aproximadamente constante (en la superficie o en el volumen del alambre) para una radio del alambre mucho más pequeña que otras escalas de longitud.
Inductancia mutua de dos bucles de alambre
La inductancia mutua por un circuito de filamento i en un circuito j filamentosa está dada por la integral doble Fórmula Neumann
El símbolo μ 0 indica la constante magnética (4π × 10 -7 H / m), C i y C j son las curvas atravesado por los cables, R ij es la distancia entre dos puntos. Ver una derivación de esta ecuación.
Autoinductancia de un asa de alambre
Formalmente, la auto-inductancia de un bucle de alambre estaría dada por la ecuación anterior con i = j. El problema, sin embargo, es que 1 / R se convierte ahora en infinito, lo que es necesario tomar el radio del alambre finito A y la distribución de la corriente en el alambre en cuenta. Quedan la contribución de la integral sobre todos los puntos con | R |> a plazo / 2 y una corrección,
Aquí una y el radio l denotan y la longitud del alambre, e Y es una constante que depende de la distribución de la corriente en el cable: Y = 0 cuando la corriente fluye en la superficie del alambre ( efecto de la piel), Y = 1/4 cuando la corriente es homogénea a través del cable. Esta aproximación es exacta cuando los cables están mucho en comparación con sus dimensiones en sección transversal.
Método de imágenes
En algunos casos diferentes distribuciones actuales generan el mismo campo magnético en alguna sección del espacio. Este hecho puede ser usado para referirse inductancias auto ( método de las imágenes). Como ejemplo, consideremos los dos sistemas:
- Un alambre a una distancia d / 2 en frente de una pared perfectamente conductor (que es el retorno)
- Dos alambres paralelos a una distancia d, con la corriente opuesta
El campo magnético de los dos sistemas coincide (en un medio espacio). La energía del campo magnético y la inductancia del segundo sistema así son dos veces tan grande como la del primero sistema.
Relación entre la inductancia y capacitancia
Inductancia por longitud L 'y capacitancia por unidad de longitud C 'están relacionados entre sí en el caso especial de líneas de transmisión formado por dos conductores perfectos paralelos de sección transversal arbitraria pero constante,
Aquí ε y μ denotar constante dieléctrica y permeabilidad magnética del medio de los conductores están incrustados en. No hay eléctrico y ningún campo magnético dentro de los conductores (completa efecto de la piel, de alta frecuencia). La corriente fluye hacia abajo en una línea y vuelve por el otro. Las señales se propagan a lo largo de la línea de transmisión a la velocidad de la radiación electromagnética en el medio no conductor que envuelve los conductores.
Autoinducción de circuitos eléctricos sencillos en el aire
La autoinducción de muchos tipos de circuitos eléctricos se puede dar en forma cerrada. Los ejemplos se enumeran en la tabla.
| Tipo | Inductancia | Comentario |
|---|---|---|
| De una sola capa solenoide | 
|  : Número de vueltas : Número de vueltas r: Radio l: Longitud w = r / l   : Integrales elípticas : Integrales elípticas |
| Cable coaxial, alta frecuencia |  | 1: Radio exterior R: Radio interior l: Longitud |
| Bucle Circular |  | r: Loop radio R: radio de alambre |
| Rectángulo |  | b, d: longitud Fronteriza d >> a, b >> una R: radio de alambre |
| Par de paralelo cables | 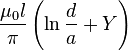 | R: radio de alambre d: Distancia, d ≥ 2 bis l: Longitud del par |
| Par de paralelo cables de alta frecuencia | 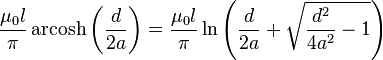 | R: radio de alambre d: Distancia, d ≥ 2 bis l: Longitud del par |
| Alambre paralelo a perfectamente pared conducir |  | R: radio de alambre d: Distancia, d ≥ a l: Longitud |
| Alambre paralelo a la realización de la pared, alta frecuencia | 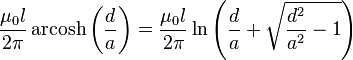 | R: radio de alambre d: Distancia, d ≥ a l: Longitud |
El símbolo μ 0 indica la constante magnética (4π × 10 -7 H / m). Para altas frecuencias la corriente eléctrica fluye en la superficie del conductor ( efecto piel), y en función de la geometría a veces es necesario distinguir inductancias alta y baja frecuencia. Este es el propósito de la constante Y: Y = 0 cuando la corriente se distribuye uniformemente sobre la superficie del alambre (efecto piel), Y = 1/4 cuando la corriente se distribuye uniformemente sobre la sección transversal del alambre. En el caso de alta frecuencia, si los conductores se aproximan entre sí, una corriente inspección adicional fluye en su superficie, y expresiones que contengan Y no serán válidas.
Inductancia con simetría física
Inductancia de un solenoide
La solenoide es un largo, la bobina delgada, es decir, una bobina cuya longitud es mucho mayor que el diámetro. En estas condiciones, y sin ningún material magnético utilizado, la densidad de flujo magnético 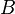 dentro de la bobina es prácticamente constante y está dada por
dentro de la bobina es prácticamente constante y está dada por
donde 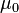 es el magnético constante,
es el magnético constante,  el número de vueltas,
el número de vueltas, 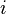 la corriente y
la corriente y 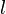 la longitud de la bobina. Ignorando efectos finales el flujo magnético total a través de la bobina se obtiene multiplicando la densidad de flujo
la longitud de la bobina. Ignorando efectos finales el flujo magnético total a través de la bobina se obtiene multiplicando la densidad de flujo 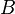 por el área de sección transversal
por el área de sección transversal  y el número de vueltas
y el número de vueltas  :
:
Cuando esto se combina con la definición de la inductancia,
se deduce que la inductancia de un solenoide está dada por:
Una tabla de inductancia para solenoides cortos de diversos diámetros a relaciones de longitud ha sido calculada por Dellinger, Whittmore y Ould
Esto, y la inductancia de formas más complicadas, se puede derivar de las ecuaciones de Maxwell . Para bobinas de núcleo de aire rígidos, la inductancia es una función de la geometría de la bobina y el número de vueltas, y es independiente de la corriente.
Un análisis similar se aplica a un solenoide con un núcleo magnético, pero sólo si la longitud de la bobina es mucho mayor que el producto de la permeabilidad relativa del núcleo magnético y el diámetro. Esto limita el análisis simple de núcleos de baja permeabilidad, o solenoides delgadas extremadamente largos. Aunque suele ser útil, las ecuaciones son,
donde 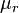 la permeabilidad relativa del material dentro del solenoide,
la permeabilidad relativa del material dentro del solenoide,
de la que se deduce que la inductancia de un solenoide está dada por:
donde N es cuadrado debido a la definición de la inductancia.
Tenga en cuenta que, dado que la permeabilidad de los materiales ferromagnéticos con los cambios de flujo magnético aplicado, la inductancia de una bobina con un núcleo ferromagnético generalmente variará con actual.
Inductancia de una línea coaxial
Deje que el conductor interior tiene un radio 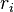 y permeabilidad
y permeabilidad  , Dejar que el dieléctrico entre el conductor interior y exterior tienen permeabilidad
, Dejar que el dieléctrico entre el conductor interior y exterior tienen permeabilidad 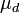 , Y dejar que el conductor externo tiene radio interior
, Y dejar que el conductor externo tiene radio interior  , Radio exterior
, Radio exterior  , Y la permeabilidad
, Y la permeabilidad 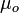 . Supongamos que una corriente continua
. Supongamos que una corriente continua 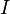 fluye en direcciones opuestas en los dos conductores, con densidad de corriente uniforme. El campo magnético generado por estas corrientes apunta en la dirección azimutal y es una función del radio de
fluye en direcciones opuestas en los dos conductores, con densidad de corriente uniforme. El campo magnético generado por estas corrientes apunta en la dirección azimutal y es una función del radio de  ; puede ser calculada utilizando La ley de Ampère:
; puede ser calculada utilizando La ley de Ampère:
El flujo por longitud 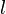 en la región entre los conductores puede ser calculada mediante la elaboración de una superficie que contiene el eje:
en la región entre los conductores puede ser calculada mediante la elaboración de una superficie que contiene el eje:
Dentro de los conductores, L puede calcularse igualando la energía almacenada en un inductor, 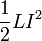 , Con la energía almacenada en el campo magnético:
, Con la energía almacenada en el campo magnético:
Para una geometría cilíndrica sin 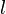 la dependencia, la energía por unidad de longitud es
la dependencia, la energía por unidad de longitud es
donde  es la inductancia por unidad de longitud. Para el conductor interior, la integral en el mano-lado es
es la inductancia por unidad de longitud. Para el conductor interior, la integral en el mano-lado es  ; para el conductor exterior que es
; para el conductor exterior que es 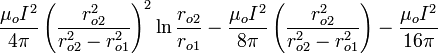
Despejando  y la suma de los términos para cada región, junto da una inductancia total por unidad de longitud:
y la suma de los términos para cada región, junto da una inductancia total por unidad de longitud:
Sin embargo, para una aplicación típica línea coaxial estamos interesados en pasar señales (no-DC) a frecuencias para las que el resistiva efecto de la piel no se puede descuidar. En la mayoría de casos, los términos conductor interior y exterior son insignificantes, en cuyo caso se puede aproximar
Análisis de circuitos de fasores y la impedancia
Uso fasores, el equivalente impedancia de una inductancia está dada por:
donde
- j es la unidad imaginaria ,
- L es la inductancia,
- ω = 2πf es la frecuencia angular,
- f es la frecuencia y
- ωL = X L es el inductivo reactancia.
Inductancia no lineal
Muchos inductores hacen uso de materiales magnéticos . Estos materiales en un amplio rango suficiente exhiben una permeabilidad no lineal con efectos tales como saturación. Esto hace que en vez de la inductancia en función de la corriente aplicada resultante. Ley de Faraday, pero aún mantiene la inductancia es ambigua y es diferente si se está calculando los parámetros de circuitos o flujos magnéticos.
La inductancia secante o de gran señal se utiliza en los cálculos de flujo. Se define como:
El diferencial o de pequeña señal inductancia, por otro lado, se utiliza en el cálculo de voltaje. Se define como:
La tensión de circuito para un inductor no lineal se obtiene a través de la inductancia diferencial como se muestra por la Ley de Faraday y la regla de la cadena de cálculo.
Existen definiciones similares para inductancias mutuas no lineales.


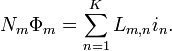



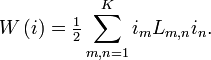








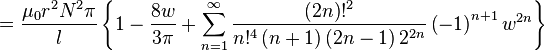
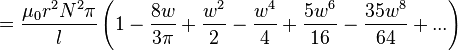 para w << 1
para w << 1  para w >> 1
para w >> 1