La logique booléenne

Contexte des écoles Wikipédia

Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays

La logique booléenne est un système complet Système de logique opérations. Il a été nommé d'après George Boole, qui a défini d'abord un système algébrique de la logique dans le milieu du 19ème siècle . La logique booléenne a de nombreuses applications dans l'électronique, du matériel informatique et des logiciels, et est la base de l'électronique numérique. En 1938 , Claude Shannon a montré comment les circuits électriques avec relais étaient un modèle pour la logique booléenne. Ce fait est vite révélée énormément consécutifs avec l'émergence de l'électronique ordinateur .

En utilisant le algèbre des ensembles, cet article contient une introduction de base à ensembles, opérations booléennes, les diagrammes de Venn , tables de vérité, et les applications booléennes. Le L'article de l'algèbre de Boole traite un type de structure algébrique qui satisfait les axiomes de la logique booléenne. L' arithmétique binaire article traite de l'utilisation des binaires chiffres dans l'ordinateur systèmes.

Réglez la logique par rapport logique booléenne

Les jeux peuvent contenir des éléments. Nous allons d'abord commencer par discuter de la logique générale de jeu, puis nous limiter à la logique booléenne, où les éléments (ou "bits") contiennent chacun seulement deux valeurs possibles, appelé divers noms, tels que «vrai» et «faux», «oui» et "non", "on" et "off", ou "1" et "0".

Termes

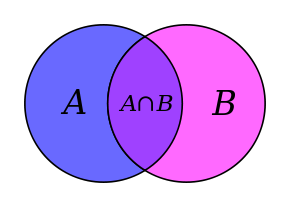
Diagramme de Venn montrant l'intersection des ensembles "A et B" (en violet / ombrage foncé), l'union des ensembles "A ou B" (toutes les régions de couleur / ombragées), et le cas OU exclusif "ensemble A XOR B" ( toutes les régions, sauf les couleurs / seules les régions ombragées légèrement violets). Le «univers» est représenté par toute la région dans le cadre rectangulaire.

Soit X un ensemble:

Un élément est un membre d'un ensemble. Ceci est indiqué par 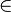$\ In$ . Si ce ne est pas un élément de l'ensemble, ce est notée $\ Pas dedans$ .

L'univers est l'ensemble X, parfois désigné par 1. Notez que cette utilisation du mot univers signifie «tous les éléments à l'étude", qui ne sont pas nécessairement les mêmes que "tous les éléments, il ya".

L'ensemble vide ou ensemble vide est l'ensemble des éléments pas, notée 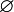$\ Varnothing$ et parfois 0.

Un opérateur unaire se applique à un ensemble unique. Il est un opérateur unaire, appelé NON logique. Il fonctionne en prenant le compléter.

Un opérateur binaire se applique aux deux ensembles. Les opérateurs binaires de base sont logiques OU et ET logique. Ils effectuent le syndicat et l'intersection des ensembles. Il ya aussi d'autres opérateurs binaires dérivés, tels que XOR (OU exclusif).

Un sous-ensemble est désigné par $A \ B subseteq$ et des moyens de chaque élément de l'ensemble A est également dans la série B.

Un sous-ensemble est désigné par $Un \ subset B$ et des moyens de chaque élément de l'ensemble A est également dans la série B et les deux ensembles ne sont pas égaux.

Un sur-ensemble est désigné par $A \ B supseteq$ et des moyens de chaque élément de l'ensemble B est également dans la série A.

Un super-bon est notée $A \ B supset$ et des moyens de chaque élément de l'ensemble B est également dans la série A et les deux ensembles ne sont pas égaux.

Exemple

Multiples booléennes de deux trois 5.svg

Imaginons que l'ensemble A contient tous les nombres pairs (multiples de deux) dans «l'univers» (défini dans l'exemple à droite, comme tous les nombres entiers compris entre 0 et 30 inclus) et l'ensemble B contient tous les multiples de trois dans "l'univers". Puis l'intersection des deux ensembles (tous les éléments dans les ensembles A et B) serait tous des multiples de six "l'univers".

Le complément de l'ensemble A (tous les éléments ne sont pas en jeu A) serait dans tous les nombres impairs "l'univers".

Chaînage opérations ensemble

Alors que tout au plus deux ensembles sont assemblés dans toute opération booléenne, le nouvel ensemble formé par cette opération peut alors être joint à d'autres jeux utilisant des opérations booléennes supplémentaires. Dans l'exemple précédent, nous pouvons définir une nouvelle série C comme l'ensemble de tous les multiples de cinq dans "l'univers". Ainsi, «ensembles A et B ET C" serait tous les multiples de 30 dans "l'univers". Si plus pratique, nous pouvons considérer mis AB à l'intersection des ensembles A et B, ou l'ensemble des multiples de six "l'univers". Ensuite, nous pouvons dire «ensembles AB et C" sont l'ensemble des multiples de 30 dans "l'univers". Nous pourrions alors prendre un peu plus loin et appeler ce jeu de résultats ABC.

L'utilisation de parenthèses

Alors que ne importe quel nombre d'ET logiques (ou ne importe quel nombre des RUP logiques) peuvent être chaînés ensemble sans ambiguïté, la combinaison de AND et OR et NOT peut conduire à des cas ambigus. Dans de tels cas, les parenthèses peuvent être utilisées pour préciser l'ordre des opérations. Comme toujours, les opérations à l'intérieur de la paire la plus interne est réalisée en premier, suivie par la paire suivante out, etc., jusqu'à ce que toutes les opérations entre parenthèses ont été accomplies. Ensuite toutes les opérations en dehors des parenthèses sont effectuées.

Application aux valeurs binaires

Dans cet exemple, nous avons utilisé des nombres naturels , tandis que dans la logique booléenne nombres binaires sont utilisés. L'univers, par exemple, peut contenir seulement deux éléments, "0" et "1" (ou "vrai" et "faux", "oui" et "non", "on" ou "off", etc.). On pourrait aussi combiner des valeurs binaires ensemble pour obtenir des mots binaires, tels que, dans le cas de deux chiffres, «00», «01», «10» et «11». Appliquer la logique ensemble à ces valeurs, nous pourrions avoir un ensemble de toutes les valeurs, où le premier chiffre est "0" ("00" et "01") et l'ensemble des valeurs où les premier et deuxième chiffres sont différents ("01" et "10"). L'intersection des deux ensembles serait alors le seul élément, "01". Cela pourrait être représentée par l'expression booléenne suivante, où "1er" est le premier chiffre et "2ème" est le deuxième chiffre:

(PAS 1er) ET (1er 2ème PAS)

Propriétés

Définissons symboles pour les deux opérations binaires primaires que 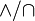$\ Terres / \ cap$ (ET logique mis intersection /) et $\ Lor / \ cup$ (OU logique / set syndicat), et pour le fonctionnement unaire unique $\ Lnot$ / ~ (NOT logique / set complément). Nous allons également utiliser les valeurs 0 (FALSE logique / l'ensemble vide) et 1 (logique VRAI / l'univers). Les propriétés suivantes se appliquent à la fois à la logique booléenne et définir logique (bien que seulement la notation pour la logique booléenne est affiché ici):

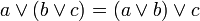
$un \ lor (b \ lor c) = (a \ lor b) \ lor c$	$un \ terres (b \ terres c) = (a \ terres b) \ c terres$	associativité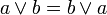
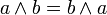
$un \ lor b = b \ lor un$	$a \ b = terres b \ terres une$	commutativité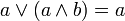
$un \ lor (une terre \ b) = a$	$un \ terres (un lor \ b) = a$	absorption
$un \ lor (b \ terres c) = (a \ lor b) \ terres (un \ lor c)$	$un \ terres (b \ lor c) = (a \ terres b) \ lor (un \ terres c)$	distributivité
$un \ lor \ lnot a = 1$	$un \ terres \ lnot a = 0$	compléments
$un \ lor a = a$	$un \ terres a = a$	idempotence
$un \ lor 0 = une$	$un \ terres 1 = a$	boundedness
$un \ lor 1 = 1$	$un \ terres 0 = 0$	boundedness
$\ Lnot 0 = 1$	$\ Lnot 1 = 0$	0 et 1 sont compléments
$\ Lnot (un \ lor b) = \ lnot un \ terres \ b lnot$	$\ Lnot (un \ terres b) = \ lnot un \ lor \ b lnot$	les lois de Morgan
$\ Lnot \ lnot a = a$		involution

Les trois premières propriétés définissent un réseau; les cinq premiers définissent un Algèbre de Boole. Les cinq autres sont la conséquence des cinq premiers.

Les tables de vérité

Pour la logique booléenne utilisant seulement deux valeurs, 0 et 1, l'intersection et l'union de ces valeurs peut être définie à l'aide tables de vérité comme celles-ci:

$\ Cap$	0	1
0	0	0
1	0	1

$\ Cup$	0	1
0	0	1
1	1	1

Plus de tables de vérité complexes impliquant plusieurs entrées, et d'autres opérations booléennes, peuvent également être créés.

Tables de vérité ont des applications dans la logique , l'interprétation de 0 comme FAUX, 1 TRUE, $\ Cap$ comme ET, $\ Cup$ que OR et NOT ¬.

Autres notations

Mathématiciens et ingénieurs utilisent souvent plus (+) pour OU et un signe du produit ( $\ Cdot$ ) Pour ET. OU et ET sont quelque peu analogue à addition et la multiplication dans d'autres structures algébriques , et cette notation, il est très facile d'obtenir somme des produits former pour l'algèbre normale. 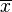Ne peut pas être représenté par une ligne tracée ci-dessus l'expression étant neutralisés ( $\ Overline {x}$ ).

Les programmeurs utilisent souvent un symbole pipe (|) pour OU, une esperluette (&) pour ET, et un tilde (~) pour PAS. Dans de nombreux langages de programmation , ces symboles représentent opérations bit à bit. «||», «&&» Et «!" sont utilisés pour des variantes de ces opérations.

Un autre utilise la notation «rencontrer» pour ET et "join" de OR. Toutefois, cela peut prêter à confusion, comme le terme "join" est aussi couramment utilisé pour toute opération booléenne qui combine jeux ensemble, qui comprend à la fois AND et OR.

L'utilisation des mathématiques de base des termes booléens

Dans le cas d'équations simultanées, ils sont connectés avec une logique implicite ET:

x + y = 2

x - y = 2

La même chose se applique aux inégalités simultanées:

x + y <2

x - y <2

Le supérieur ou signe égal ( $\ Ge$ ) Et inférieur ou signe égal ( $\ Le$ ) Peut être supposé contenir un OU logique:

X <2

X = 2

Le signe plus / moins ( 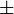$\ H$ ), Comme dans le cas de la solution à un problème de racine carrée, peut être considéré comme logique OU:

WIDTH = 3

WIDTH = -3

Anglais utilisation de la langue des termes booléens

Des précautions doivent être prises lors de la conversion d'une phrase anglaise dans une déclaration formelle booléenne. Beaucoup de phrases en anglais ont des significations imprécises, par exemple "Tout ce qui brille ne est pas or», ce qui pourrait signifier que «rien de ce qui brille est or» ou «certaines choses qui scintillent sont pas de l'or".

ET et OU peut également être utilisé de manière interchangeable en anglais, dans certains cas:

"Je ai toujours un parapluie quand il pleut et il neige."

"Je ai toujours un parapluie quand il pleut ou qu'il neige."

Parfois, les mots anglais ET et OU ont le sens opposé dans la logique booléenne:

"Donnez-moi tous les fruits rouges et bleus» signifie généralement «Donne-moi toutes les baies qui sont rouges ou bleu". Un phrasé alternative pour l'anglais standard écrit: "Donnez-moi tous les petits fruits qui sont rouges ainsi que toutes les baies qui sont bleus".

Notez également que le mot OU en anglais peuvent correspondre soit logique OU ou XOR logique, selon le contexte:

«Je commence à transpirer quand l'humidité ou la température est élevée." (OU logique)

"Vous voulez la crème glacée et des bonbons? Vous pouvez avoir de la crème glacée ou des bonbons." (XOR logique)

La combinaison ET / OU est parfois utilisé en anglais pour spécifier un OU logique, quand juste un mot ou une seule pourrait s'être trompé en ce sens logique XOR:

«Je vais avoir du poulet et / ou de bœuf pour le dîner." (OU logique). Un phrasé alternative pour la norme de l'anglais écrit: «Je vais avoir du poulet ou du bœuf, ou les deux, pour le dîner."

L'utilisation de «et / ou» virgule est généralement défavorisée dans formelle anglais écrit. Une telle utilisation peut introduire imprécision critique dans les instruments juridiques, les résultats de recherche, et les spécifications des programmes informatiques ou des circuits électroniques.

Un cas où ce est un problème, ce est quand les spécifications d'un programme d'ordinateur ou circuit électronique sont fournis comme un paragraphe en anglais décrivant leur fonction. Par exemple, l'instruction: "le programme doit vérifier que le demandeur a vérifié l'homme ou la boîte femelle", doit être pris comme un XOR, et un chèque ajoutée pour se assurer que l'un, et un seul, boîte est sélectionné. Dans d'autres cas, l'interprétation de l'anglais peut être moins certaine, et l'auteur de la spécification peut être consultée afin de déterminer leur véritable intention.

Applications

Conception de circuits électroniques numériques

La logique booléenne est également utilisé pour la conception de circuits en génie électrique ; ici 0 et 1 peuvent représenter les deux états différents d'un bit dans un circuit numérique, généralement haute et basse tension. Les circuits sont décrits par des expressions contenant des variables, et deux de ces expressions sont égales pour toutes les valeurs des variables si, et seulement si, les circuits correspondants ont le même comportement d'entrée-sortie. En outre, chaque comportement possible d'entrée-sortie peut être modélisé par une expression booléenne approprié.

De base des portes logiques tels que ET, OU et NON portes peuvent être utilisés seuls, ou en combinaison avec NAND, NOR, et portes XOR, pour contrôler l'électronique numérique et des circuits. Que ces portes sont câblés en série ou en parallèle des contrôles de la priorité des opérations.

applications de base de données

Bases de données relationnelles utilisent SQL ou d'autres langues spécifiques à la base, d'exécuter des requêtes, qui peut contenir la logique booléenne. Pour cette application, chaque enregistrement dans un tableau peut être considéré comme un "élément" d'un "set". Par exemple, dans SQL, ceux-ci Instructions SELECT sont utilisés pour récupérer des données à partir des tables dans la base de données:

    SELECT * FROM employés lorsque LAST_NAME = 'Smith' ET prenom = 'John';

    SELECT * FROM employés lorsque LAST_NAME = 'Smith' OU prenom = 'John';

    SELECT * FROM Employees WHERE NOT LAST_NAME = 'Smith';

Les parenthèses peuvent être utilisés pour spécifier explicitement l'ordre dans lequel les opérations booléennes se produisent, lorsque plusieurs opérations sont présents:

    SELECT * FROM Employees WHERE (PAS LAST_NAME = 'Smith') ET (FIRST_NAME = 'John' OU FIRST_NAME = 'Mary');

Plusieurs jeux de parenthèses imbriquées peuvent également être utilisés, si nécessaire.

Toute opération booléenne (ou opérations) qui combine deux (ou plusieurs) des tables ensemble est appelé une jointure, dans la terminologie de base de données relationnelle.

Dans le domaine de Dossiers médicaux électroniques, des applications logicielles utilisent la logique booléenne pour interroger leurs bases de données de patients, dans ce qui a été nommé La technologie de traitement de Concept.

les requêtes des moteurs de recherche

les requêtes des moteurs de recherche utilisent également la logique booléenne. Pour cette application, chaque page web d'Internet peut être considéré comme un "élément" d'un "set". Les exemples suivants utilisent une syntaxe soutenu par Google .

Doublequotes sont utilisés pour combiner des mots séparés par un espace en un seul terme de recherche.
Les espaces est utilisé pour spécifier ET logique, car il est l'opérateur par défaut pour rejoindre termes de recherche:

    "Chercher terme une" "terme de recherche 2"

Le mot-clé est utilisé pour OU OU logique:

    "Le terme de recherche 1» ou «Recherche terme 2"

Le signe moins est utilisé pour NOT logique (et non):

    "Le terme de recherche 1" - "Chercher terme 2"

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Boolean_logic&oldid=194646149 "

Privacy Policy and Contacts (IT)