Nombre binaire

Renseignements généraux

SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Cliquez ici pour plus d'informations sur les enfants SOS.

Systèmes de numération par la culture
Chiffres indo-arabes Western Arabe Est Arabe Famille indienne Tamil Telugu Birman Khmer Lao Mongol Thaï Chiffres Asie de l'Est Chinois Japonais Suzhou Coréen Vietnamien Compter tiges Chiffres alphabétiques Abjad Arménien Aryabhata Cyrillique Ge'ez Grecque Géorgien Hébreu D'autres systèmes historiques Égéen Grenier Babylonien Brahmi Égyptien Étrusque Inuits Kharosthî Maya Quipu Romain
Systèmes de positionnement par base
Decimal (10)
1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 20 24 26 27 32 36 60 64 85
Ternaire équilibré
Liste des systèmes de numération

Le système de numération binaire, ou une base 2-système numérique, est un système numérique qui représente des valeurs numériques en utilisant deux symboles, habituellement 0 et 1 . Plus précisément, l'habitude base- 2 est un système avec une notation de position radix de 2. En raison de sa mise en œuvre simple dans circuits électroniques, le système binaire est utilisé en interne par tous les modernes ordinateurs .

Histoire

L'ancien écrivain indien Pingala développé des concepts mathématiques avancés pour décrire prosodie, et ce faisant, a présenté la première description connue d'un système de numération binaire, peut-être dès le 8ème siècle avant JC. D'autres le placent beaucoup plus tard; R. Hall, Mathématiques de la poésie, a "c. 200 BC». Le système de numérotation est basée sur la Eye of Horus Ancien Empire système de numération.

Un ensemble complet de huit trigrammes et 64 hexagrammes, analogues aux trois bits et 6 bits chiffres binaires, étaient connus des anciens Chinois dans le texte classique I Ching . Ensembles de combinaisons binaires similaires ont également été utilisés dans des systèmes de divination africains traditionnels tels que Ifá ainsi que dans l'Ouest médiévale géomancie.

Un arrangement binaire ordonnée des hexagrammes du Yi King, représentant la séquence décimal 0-63, et une méthode pour générer le même, a été développé par le savant et philosophe chinois Shao Yong dans le 11ème siècle. Cependant, il ne existe aucune preuve que Shao compris calcul binaire.

En 1605, Francis Bacon a discuté d'un système par lequel les lettres de l'alphabet peuvent être réduits à des séquences de chiffres binaires, qui pourrait alors être codés en variations peine visibles dans la police dans ne importe quel texte aléatoire. Il est important pour la théorie générale de codage binaire, il a ajouté que cette méthode pourrait être utilisée avec des objets à tous: "à condition que ces objets soient capables d'une double seule différence, comme par Bells, par Trompettes, par les lumières et lampes de poche, par le rapport des mousquets, et des instruments de même nature ". (Voir Le chiffrement de Bacon.)

Le système de nombre binaire moderne a été entièrement documenté par Gottfried Leibniz au 17e siècle dans son article Explication de l'Arithmétique Binaire . Le système de Leibniz utilisé 0 et 1, comme le système de numération binaire moderne.

En 1854, la Colombie- mathématicien George Boole a publié un document historique détaillant un système algébrique de la logique qui deviendrait connue comme Algèbre de Boole. Son calcul logique était de devenir contribué à la conception de circuits électroniques numériques.

En 1937, Claude Shannon a produit son mémoire de maîtrise à MIT qui a mis Algèbre de Boole et l'arithmétique binaire en utilisant les relais et les interrupteurs électroniques pour la première fois dans l'histoire. Intitulée Une analyse symbolique de relais et de circuits de commutation, la thèse de Shannon essentiellement fondée pratique conception de circuits numériques.

En Novembre 1937, George Stibitz, qui travaillait alors au Les Bell Labs, a complété un ordinateur à base de relais qu'il a baptisé la "Modèle K» (pour «K itchen", où il avait réuni il), qui a calculé en utilisant addition binaire. De Bell Labs autorisé ainsi un programme de recherche complet à la fin de 1938 avec Stibitz à la barre. Leur Nombre complexe informatique, complété 8 janvier 1940 , a été en mesure de calculer les nombres complexes . Lors d'une démonstration à la Conférence American Mathematical Society au Dartmouth College sur 11 septembre, 1940 , Stibitz a pu envoyer le Complex Number Calculator commandes à distance sur des lignes téléphoniques par un téléscripteur. Ce était la première machine informatique déjà utilisé à distance via une ligne téléphonique. Certains participants de la conférence qui ont été témoins de la manifestation étaient John Von Neumann , John Mauchly et Norbert Wiener, qui a écrit à ce sujet dans ses mémoires.

Représentation

Un certain nombre binaire peut être représenté par ne importe quelle séquence de les bits (chiffres binaires), qui à leur tour peuvent être représentés par ne importe quel mécanisme capable de se trouver dans deux états mutuellement exclusifs. Les séquences suivantes de symboles pourraient tous être interprétés comme la même valeur numérique binaire de 667:

 1 0 1 0 0 1 1 0 1 1
 | - | - - | | - | |
 xoxooxxoxx
 ynynnyynyy

Un Binary Clock pourrait utiliser LED d'exprimer des valeurs binaires. Dans cette horloge, chaque colonne de LED montre une codé en binaire chiffre décimal de la traditionnelle temps sexagésimal.

La valeur numérique représentée dans chaque cas dépend de la valeur affectée à chaque symbole. Dans un ordinateur, les valeurs numériques peuvent être représentés par deux différents tensions; sur un magnétique disque, magnétique polarités peuvent être utilisés. Un «positif», «oui», ou «on» ne est pas nécessairement équivalente à la valeur numérique d'un; il dépend de l'architecture utilisée.

En accord avec la représentation habituelle des chiffres en utilisant les chiffres arabes , nombres binaires sont généralement écrits en utilisant les symboles 0 et 1. Lorsque écrite, chiffres binaires sont souvent indicés, préfixe ou un suffixe pour indiquer leur base, ou racine. Les notations suivantes sont équivalentes:

100101 binaire (déclaration explicite format)

100101b (suffixe indiquant un format binaire)

100101B (suffixe indiquant un format binaire)

bin 100 101 (un préfixe indiquant format binaire)

100 101 ₂ (d'un indice indiquant en base 2 (binaire) la notation)

% 100 101 (un préfixe indiquant format binaire)

0b100101 (un préfixe indiquant format binaire, courante dans les langages de programmation)

Lorsque parlé, chiffres binaires sont généralement lus chiffre par chiffre, afin de les distinguer des nombres décimaux. Par exemple, le binaire numérique 100 est prononcé un zéro zéro, plutôt que d'une centaine, de faire sa nature binaire explicite, et à des fins de correction. Étant donné que le chiffre binaire 100 est égale à la valeur décimale de quatre, il serait source de confusion, et numériquement incorrecte, se référer à la référence numérique comme cent.

Compter en binaire

Binaire	Décimal
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10

Comptage en binaire est similaire à compter dans tout autre système de numération. Commençant par un seul chiffre, compter produit par chaque symbole, dans l'ordre croissant. Comptage décimal utilise les symboles 0 à 9, tandis que binary ne utilise que les symboles 0 et 1.

Lorsque les symboles pour le premier chiffre sont épuisées, le chiffre immédiatement supérieur (à gauche) est incrémenté, et le comptage recommence à 0. En décimal , comptant produit comme ceci:

000, 001, 002, ... 007, 008, 009, (le plus à droite chiffre recommence, et chiffre suivant est incrémenté)

0 1 0, 011, 012, ...

...

090, 091, 092, ... 097, 098, 099, (plus à droite deux chiffres recommencer, et chiffre suivant est incrémenté)

1 00, 101, 102, ...

Après un chiffre atteint 9, une augmentation réinitialise à 0, mais provoque également une augmentation du chiffre suivant à gauche. En binaire, de comptage est le même, sauf que seules les deux symboles 0 et 1 sont utilisés. Ainsi, après un chiffre atteint 1 en binaire, une augmentation réinitialise à 0, mais provoque également une augmentation du chiffre suivant à gauche:

000, 001, (le plus à droite chiffres recommence, et chiffre suivant est incrémenté)

0 1 0, 011, (plus à droite deux chiffres recommencer, et chiffre suivant est incrémenté)

1 00, 101, ...

Arithmétique binaire

Arithmétique en binaire est un peu comme l'arithmétique dans d'autres systèmes de numération. Addition, soustraction, multiplication et division peuvent être effectuées sur des chiffres binaires.

Addition

Le schéma de circuit pour un binaire demi-additionneur, qui ajoute deux bits ensemble, la production de somme et de retenue bits.

Le plus simple opération arithmétique binaire est en outre . Ajout de deux nombres binaires à un seul chiffre est relativement simple:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10 (report: 1)

Ajout de deux valeurs "1" produit la valeur "10" (parlé comme "un-zéro"), équivalent à la valeur décimale 2. Ceci est similaire à ce qui se passe en décimal lorsque certains nombres à un chiffre sont additionnés; si le résultat est égal ou supérieur à la valeur de la base (10), le chiffre à gauche est incrémenté:

5 + 5 = 10

7 + 9 = 16

Ceci est connu comme la réalisation dans la plupart des systèmes de numération. Lorsque le résultat d'une addition dépasse la valeur de la base, la procédure est de "transporter la une" vers la gauche, de l'ajouter à la valeur de position suivante. Porter des œuvres de la même façon en binaire:

   1 1 1 1 1 (chiffres réalisés)
     0 1 1 0 1
 + 1 1 0 1 1
 -------------
 = 1 0 0 1 0 0

Dans cet exemple, deux chiffres sont additionnés: 01101 ₂ (13 décimal) et 10 111 ₂ (23 décimal). La rangée du haut montre les bits de report utilisés. À partir de la colonne de droite, 1 + 1 = ₂ 10. Le 1 est effectuée vers la gauche, et le 0 est écrit au bas de la colonne de droite. La deuxième colonne de la droite est ajouté: 1 + 0 + 1 = 10 ₂ à nouveau; l'une est effectuée, et 0 est écrit au bas. La troisième colonne: 1 + 1 + 1 = 11 ₂ Cette fois, un 1 est effectuée, et un 1 est écrit dans la rangée du bas.. Procéder de cette façon donne la réponse finale ₂ 100 100 (36 décimal).

Lorsque les ordinateurs doivent additionner deux nombres, la règle selon laquelle: x ^ y = x + y% 2 pour deux bits x et y permet de calculer très rapide, aussi bien.

Soustraction

Soustraction fonctionne de la même manière:

0 - 0 = 0

0-1 = 1 (avec emprunt)

1-0 = 1

1 - 1 = 0

Un chiffre binaire peut être soustraite de l'autre comme suit:

     * * * * (Colonnes étoilés sont empruntés)
   1 1 0 1 1 1 0
 - 1 0 1 1 1
 ----------------
 = 1 0 1 0 1 1 1

Soustrayant un nombre positif est équivalent à l'ajout d'un négatif nombre d'égale valeur absolue ; ordinateurs utilisent généralement la notation en complément à deux pour représenter les valeurs négatives. Cette notation élimine la nécessité d'une opération distincte "soustraction". La soustraction peut se résumer par cette formule:

A - B = A + B + 1 pas

Pour plus de détails, voir le complément à deux.

Multiplication

Multiplication en binaire est similaire à son homologue décimal. Deux nombres A et B peuvent être multipliées par produits partiels: pour chacun des chiffres B, le produit de ce chiffre dans A est calculé et écrit sur une nouvelle ligne, décalé vers la gauche de sorte que ses lignes de chiffres les plus à droite aligne avec le chiffre B qui était utilisé. La somme de tous ces produits partiels donne le résultat final.

Comme il n'y a que deux chiffres en binaire, il n'y a que deux résultats possibles de chaque multiplication partielle:

Si le chiffre B = 0, le produit partiel est aussi 0
Si le chiffre B = 1, le produit partiel est égal à A

Par exemple, les nombres binaires 1011 et 1010 sont multipliés comme suit:

            1 0 1 1 (A)
          × 1 0 0 1 (B)
          ---------
            0 0 0 0 ← correspond à un zéro à B
    + 1 0 1 1 ← correspond à une une en B
    + 0 0 0 0  
    + 1 0 1 1  
    ---------------
    = 1 1 0 1 1 1 0

Les nombres binaires peuvent également être multipliés avec des morceaux après un virgule binaire:

                1 0 1,1 0 1 (A) (5,625 en décimal)
              × 1 1 0,0 1 (B) (6,25 en décimal)
              -------------
                1 0 1 1 0 1 ← correspond à une une en B
    + 0 0 0 0 0 0 ← correspond à un zéro à B
    + 0 0 0 0 0 0
    + 1 0 1 1 0 1
    + 1 0 1 1 0 1
    -----------------------
    = 1 0 0 0 1 0 1 0 1.0 1 (35,15625 en décimal)

Voir également L'algorithme de multiplication de Booth.

Division

Binary division est à nouveau similaire à son homologue décimales:

         __________
 1 0 1 | 1 1 0 1 1

Ici, le diviseur est 101 _2, ou 5 décimales, tandis que le dividende est 11011 _2, ou 27 décimal. La procédure est la même que celle de décimal la division de long; ici, le diviseur 101 ₂ va dans les trois premiers chiffres 110 ₂ du dividende une fois, donc un "1" est écrit sur la première ligne. Ce résultat est multiplié par le diviseur, et soustrait les trois premiers chiffres du dividende; le chiffre suivant ("1") est inclus pour obtenir une nouvelle séquence à trois chiffres:

              1
         __________
 1 0 1 | 1 1 0 1 1
        - 1 0 1
          -----
            0 1 1

La procédure est ensuite répétée avec la nouvelle séquence, continue jusqu'à ce que les chiffres du dividende ont été épuisées:

              1 0 1
         __________
 1 0 1 | 1 1 0 1 1
        - 1 0 1
          -----
            0 1 1
          - 0 0 0
            -----
              1 1 1
            - 1 0 1
              -----
                1 0

Ainsi, le quotient de 11 011 divisé par ₂ 101 ₂ 101 ₂ est, comme indiqué sur la première ligne, tandis que le reste, indiqué sur la ligne de fond, est de 10 _2. En décimal, 27 divisé par 5 est 5, avec un reste de 2.

Opérations bit à bit

Bien que non directement liés à l'interprétation numérique de symboles binaires, des séquences de bits peuvent être manipulées en utilisant Boolean des opérateurs logiques. Quand une chaîne de symboles binaires est manipulé de cette manière, il est appelé un opération binaire; les opérateurs logiques ET, OR, et XOR peut être effectuée sur les bits correspondants de deux nombres binaires fournis en entrée. La logique PAS opération peut être réalisée sur des bits individuels dans un seul chiffre binaire fourni en entrée. Parfois, ces opérations peuvent être utilisés comme raccourcis arithmétiques, et peuvent avoir d'autres avantages de calcul ainsi. Par exemple, un décalage arithmétique à gauche d'un nombre binaire est l'équivalent d'une multiplication par (, entier positif) la puissance de deux.

Conversion vers et à partir d'autres systèmes de numération

Décimal

Pour convertir un entier en base 10 chiffre à sa base-2 (binaire) équivalente, le nombre est divisé par deux, et le reste est le bit le moins significatif. Le (entier) résultat est à nouveau divisé par deux, sa reste est le bit le plus significatif suivant. Ce processus se répète jusqu'à ce que le résultat de division supplémentaire devient nulle.

Par exemple, ₁₀ 118, en binaire, est:

Opération	Reste
118 ÷ 2 = 59	0
59 ÷ 2 = 29	1
29 ÷ 2 = 14	1
14 ÷ 2 = 7	0
7 ÷ 2 = 3	1
3 ÷ 2 = 1	1
1 ÷ 2 = 0	1

La lecture de la séquence de restes de bas en haut donne le chiffre binaire 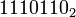$1110110_2$ .

Cette méthode fonctionne pour la conversion d'une base quelconque, mais il existe de meilleures méthodes de bases qui sont des puissances de deux, tels que octal et hexadécimal donnés ci-dessous.

Pour convertir de la base-2 à base 10 est l'algorithme inverse. A partir de la gauche, doubler le résultat et ajouter le chiffre suivant jusqu'à ce qu'il n'y ait plus. Par exemple, pour convertir 110010101101 ₂ à décimales:

Résultat	Chiffres restants
0	110010101101
0 × 2 + 1 = 1	10010101101
1 × 2 + 1 = 3	0010101101
3 × 2 + 0 = 6	010101101
6 × 2 + 0 = 12	10101101
12 x 2 + 1 = 25	0101101
25 x 2 + 0 = 50	101101
50 x 2 + 1 = 101	01101
101 × 2 + 0 = 202	1101
202 × 2 + 1 = 405	101
405 × 2 + 1 = 811	01
811 × 2 + 0 = 1622	1
1622 × 2 + 1 = 3245

Le résultat est ₁₀ 3,245.

    Binary: 1 1 0 0 1 0 1 0 1 1 0 1
  
   Décimal: [(2 ^ 11) * 1] + [(2 ^ 10) * 1] + [(2 ^ 9) * 0] + [(2 ^ 8) * 0] + [(2 ^ 7) * 1 ] + [(2 ^ 6) * 0] + [(2 ^ 5) * 1] + [(2 ^ 4) * 0] + [(2 ^ 3) * 1] + [(2 ^ 2) * 1 ] + [(2 ^ 1) * 0] + [(2 ^ 0) * 1] = 3245

Les parties fractionnaires d'un certain nombre sont convertis avec des méthodes similaires. Ils sont de nouveau fondées sur l'équivalence de décalage avec doubler ou réduire de moitié.

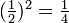Dans un nombre binaire fractionnée comme ,11010110101 _2, le premier chiffre est $\ Begin {matrix} \ frac {1} {2} \ end {matrix}$ , Le second $\ Begin {matrix} (\ frac {1} {2}) ^ 2 = \ frac {1} {4} \ end {matrix}$ , Etc. Donc, si il ya un 1 dans la première place après la virgule, le nombre est au moins $\ Begin {matrix} \ frac {1} {2} \ end {matrix}$ , Et vice versa. Double de ce nombre est au moins 1. Cela suggère l'algorithme: à plusieurs reprises le double du nombre à convertir, fiche si le résultat est au moins 1, puis jeter la partie entière.

Par exemple, $\ Begin {matrix} (\ frac {1} {3}) \ end {matrix}$ _10, en binaire, est:

Conversion	Résultat
$\ Begin {matrix} \ frac {1} {3} \ end {matrix}$	0.
$\ Begin {matrix} \ frac {1} {3} \ times 2 = \ frac {2} {3} <1 \ end {matrix}$	0.0
$\ Begin {matrix} \ frac {2} {3} \ times 2 = 1 \ frac {1} {3} \ ge 1 \ end {matrix}$	0,01
$\ Begin {matrix} \ frac {1} {3} \ times 2 = \ frac {2} {3} <1 \ end {matrix}$	0,010
$\ Begin {matrix} \ frac {2} {3} \ times 2 = 1 \ frac {1} {3} \ ge 1 \ end {matrix}$	0,0101

Ainsi, en répétant la fraction décimale 0. 3 ... est équivalente à la fraction binaire 0. répétant 01 ....

Ou par exemple, ₁₀ 0,1, en binaire, est:

Conversion	Résultat
0,1	0.
0,1 x 2 = 0,2 <1	0.0
0,2 x 2 = 0,4 <1	0,00
0,4 x 2 = 0,8 <1	0,000
0,8 x 2 = 1,6 ≥ 1	0,0001
0,6 x 2 = 1,2 ≥ 1	0,00011
0,2 x 2 = 0,4 <1	0.000110
0,4 x 2 = 0,8 <1	0.0001100
0,8 x 2 = 1,6 ≥ 1	0.00011001
0,6 x 2 = 1,2 ≥ 1	0,000110011
0,2 x 2 = 0,4 <1	0,0001100110

Ce est aussi une fraction binaire répétitive 0,00011 ... 0011. Il peut venir comme une surprise que de terminaison fractions décimales peuvent avoir expansions répétition en binaire. Ce est pour cette raison que beaucoup sont surpris de découvrir que 0,1 + 0,1 + ..., (10 ajouts) diffère de 1 à virgule flottante. En fait, les seules fractions binaires avec des extensions de terminaison sont de la forme d'un nombre entier, divisé par une puissance de 2, ce qui ne est pas 10/01.

La conversion finale est de binaire en décimal fractions. La seule difficulté se pose avec des fractions de répétition, mais sinon, la méthode est de faire passer la fraction d'un nombre entier, le convertir comme ci-dessus, puis diviser par le pouvoir approprié de deux dans la base décimale. Par exemple:

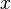
$x$	=	1100	.1011100 11100 ...
$x \ times 2 ^ 6$	=	1100101110	0,01110 01110 ...
$x \ times 2$	=	11001	0,01110 01110 ...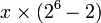
$x \ times (2 ^ 6-2)$	=	1100010101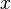
$x$	=	(789/62) ₁₀

Une autre façon de conversion de binaire en décimal, souvent plus rapide pour une personne familière avec hexadécimale , est de le faire indirectement première conversion ( 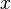$x$ en binaire) en ( 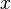$x$ en hexadécimal), puis en convertissant ( 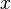$x$ en hexadécimal) dans ( 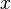$x$ en décimal).

Pour un très grand nombre, ces méthodes simples sont inefficaces parce qu'ils remplissent un grand nombre de multiplications ou des divisions, où l'un des opérandes est très grande. Un algorithme simple diviser pour régner est asymptotiquement plus efficace: étant donné un nombre binaire, nous divisons par 10 ^k, où k est choisi de manière que le quotient équivaut à peu près le reste, puis chacune de ces pièces est converti en décimal et les deux sommes concaténée. Compte tenu d'un nombre décimal, nous divisons en deux morceaux d'environ la même taille, convertir chaque binaire, puis multiplier la première pièce de 10 ^k et ajoutez-les, où k est le nombre de chiffres dans le moins significatif (le plus à droite) pièce .

Hexadécimal

Peut être converti en binaire et à partir hexadécimal un peu plus facilement. Cela est dû au fait que le base du système hexadécimal (16) est une puissance de la base du système binaire (2). Plus précisément, 16 = 2 ^4, donc il prend quatre chiffres de binaire pour représenter un chiffre d'hexadécimal.

Le tableau suivant montre chaque chiffre hexadécimal avec la valeur décimale équivalente et la séquence binaire à quatre chiffres:

Hex	Décembre	Binaire
0	0	0000
1	1	0001
2	2	0010
3	3	0011

Hex	Décembre	Binaire
4	4	0100
5	5	0101
6	6	0110
7	7	0111

Hex	Décembre	Binaire
8	8	1000
9	9	1001
Un	10	1010
B	11	1011

Hex	Décembre	Binaire
C	12	1100
Ré	13	1101
E	14	1110
Fa	15	1111

Pour convertir un nombre hexadécimal en son équivalent binaire, remplacer simplement les chiffres binaires correspondant:

3A 0011 1010 ₁₆ = ₂

E7 = ₁₆ 1110 0111 ₂

Pour convertir un nombre binaire en son équivalent hexadécimal, le diviser en groupes de quatre bits. Si le nombre de bits ne est pas un multiple de quatre, il suffit d'insérer les bits supplémentaires 0 à gauche (appelée padding). Par exemple:

01010010 ₂ 0101 0010 = groupé avec rembourrage = 52 ₁₆

11011101 ₂ 1101 1101 = groupés DD = ₁₆

Pour convertir un nombre hexadécimal en son équivalent décimale, multiplier l'équivalent décimal de chaque chiffre hexadécimal par la puissance correspondante de 16 et ajoutez les valeurs qui en résultent:

C0E7 ₁₆ = (12 x 16 ³⁾ + ⁽² x 16 0) + (14 × 16 ¹⁾ + (7 × 16 ⁰⁾ = (12 x 4,096) + (0 x 256) + (14 x 16) + ( 7 × 1) = 49 383 ₁₀

Octal

Binaire est facilement converti en le octal système de numération, depuis octal utilise une base de 8, qui est un puissance de deux (à savoir, 2 ^3, de sorte qu'il prend exactement trois chiffres binaires pour représenter un chiffre octal). La correspondance entre octal et les chiffres binaires est le même que pour les huit premiers chiffres du hexadécimale dans le tableau ci-dessus. Binaire 000 est équivalent au chiffre octal 0, binaire 111 est équivalent à octal 7, et ainsi de suite.

Octal	Binaire
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Conversion de octal au produit binaires de la même façon qu'il le fait pour hexadécimal :

65 _{8 2} 101 110 =

17 _{8 2} 111 001 =

Et de binaire en octal:

₂ = 101 100 101 100 ₂ 54 ₈ = regroupés

10 011 ₂ 010 011 ₂ = groupé avec rembourrage = 23 ₈

Et à partir de octal en décimal:

65 ₈ = (6 x 8 ¹⁾ + (5 x 8 ⁰⁾ = (6 x 8) + (5 x 1) = 53 ₁₀

127 ₈ = (1 × 8 ²⁾ + (2 x 8 ¹⁾ + (7 × 8 ⁰⁾ = (1 x 64) + (2 x 8) + (7 x 1) = 87 ₁₀

Représentant des nombres réels

Non entiers peuvent être représentés en utilisant des puissances négatives, qui sont fixés hors des autres chiffres au moyen d'un point de base (appelé virgule dans le système décimal). Par exemple, le nombre binaire 11,01 ₂ signifie donc:

1 × 2 ¹	(1 x 2 = 2)	plus
1 × 2 ⁰	(1 x 1 = 1)	plus
0 × 2 ^-1	(0 x ½ = 0)	plus
1 × 2 ^-2	(1 x ¼ = 0,25)

Pour un total de 3,25 décimal.

Tous nombres rationnels dyadiques 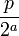$\ Frac {p} {2} ^ un$ avoir un chiffre-la représentation binaire binaire terminaison a un nombre fini de termes après le point de base. Autres nombres rationnels ont représentation binaire, mais au lieu de terminaison, ils se reproduisent, avec une séquence finie de chiffres répéter indéfiniment. Par exemple

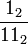$\ Frac {1_ {10}} {{3_ 10}}$ = $\ Frac {} {1_2 11_2}$ = 0.01010101 01 ₂ ...

$\ Frac {12_ {10}} {{17_ 10}}$ = $\ Frac {} {1100_2 10001_2}$ = 0.10110100 10110100 10110100 ₂ ...

Le phénomène que la représentation binaire de toute rationnelle est soit terminaison ou périodique, se produit également dans d'autres systèmes de numération à base radix. Voir, par exemple, l'explication en décimal . Une autre similarité est l'existence de représentations alternatives pour ne importe quelle représentation de terminaison, en se fondant sur le fait que 0.111111 ... est la somme de la série géométrique 2 ^{-1 -2} + 2 + 2 + ^-3 ... qui est une.

Chiffres binaires qui ne terminent ni reviennent représenter des nombres irrationnels . Par exemple,

0,10100100010000100000100 .... a un modèle, mais ce ne est pas un motif récurrent de longueur fixe, de sorte que le nombre est irrationnel
1,0110101000001001111001100110011111110 ... est la représentation binaire de 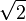$\ Sqrt {2}$ , La racine carrée de 2, un autre irrationnelle. Il n'a pas de tendance perceptible, même si une preuve que 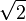$\ Sqrt {2}$ est irrationnel nécessite plus que cela. Voir nombre irrationnel .

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Binary_number&oldid=199520345 "

Privacy Policy and Contacts (IT)