Système de coordonnées cartésiennes

Figue. 1 - système de coordonnées cartésiennes. Quatre points sont marqués: (2,3) en vert, (-3,1) en rouge, (-1,5, -2,5) en bleu et (0,0), l'origine, en jaune.

Figue. 2 - système de coordonnées cartésiennes avec le cercle de rayon 2 centrée à l'origine marquée en rouge. L'équation du cercle est x ² + y ² = 4.

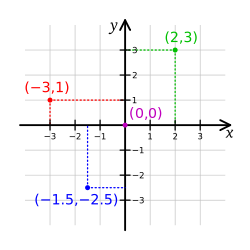
En mathématiques , le système de coordonnées cartésiennes (également appelé système de coordonnées rectangulaires) est utilisé pour déterminer chaque signaler unique dans un avion par deux nombres , généralement appelés les coordonnées x ou abscisse et l'ordonnée ou ordonnée du point. Pour définir les coordonnées, deux perpendiculaire lignes dirigées (l'axe de-x, et l'axe des y), sont précisés, ainsi que la unité de longueur, qui est délimité sur les deux axes (voir Figure 1). Des systèmes de coordonnées cartésiennes sont également utilisés dans espace (où trois coordonnées sont utilisés) et dimensions supérieures.

Utilisation du système de coordonnées cartésiennes, géométriques (telles que des formes courbes ) peuvent être décrits par algébriques équations , nommément équations satisfaites par les coordonnées des points situés sur la forme. Par exemple, le cercle de rayon 2 peut être décrit par l'équation x ² + y ² = 4 (voir figure 2).

Histoire

Des moyens cartésiennes relatives à la française mathématicien et philosophe René Descartes (latin: Cartesius), qui, entre autres choses, a travaillé à fusionner l'algèbre et de la géométrie euclidienne . Ce travail a été déterminant dans le développement de la géométrie analytique , le calcul , et cartographie.

L'idée de ce système a été développé en 1637 dans deux écrits par Descartes et indépendamment par Pierre de Fermat , bien que Fermat n'a pas publié la découverte. Dans la deuxième partie de son Discours de la méthode, Descartes introduit la nouvelle idée de spécifier la position d'un point ou un objet sur une surface, en utilisant deux axes qui se croisent comme des guides de mesure. En La Géométrie, il explore davantage les concepts mentionnés ci-dessus.

Bidimensionnelle système de coordonnées

Figue. 3 - Les quatre quadrants d'un système de coordonnées cartésiennes. Les flèches sur les axes indiquent qu'elles se étendent à jamais dans leurs directions respectives (ce est à dire à l'infini).

Un cartésien système de coordonnées en deux dimensions est généralement définie par deux axes, à angle droit les uns aux autres, formant un plan (une Plane xy). Le axe horizontal x est normalement marqué, et la axe vertical est normalement étiqueté y. Dans un système de coordonnées tridimensionnelles, d'un autre axe, z normalement marqué, on ajoute, en fournissant une troisième dimension de l'espace de mesure. Les axes sont communément définis comme mutuellement orthogonal à l'autre (chacun à angle droit par rapport l'autre). (Les premiers systèmes autorisés axes "obliques", ce est-axes qui ne répondaient pas à angle droit, et ces systèmes sont parfois utilisés aujourd'hui, bien que la plupart du temps que des exercices théoriques.) Tous les points dans un système de coordonnées cartésiennes pris ensemble forment un soi- appelé plan cartésien. Les équations qui utilisent le système de coordonnées cartésiennes sont appelées équations cartésiennes.

Le point d'intersection, où les axes se rencontrent, est appelé l'origine O normalement marqué. Les axes x et y définissent un plan qui est désigné sous le plan xy. Compte tenu de chaque axe, choisir une unité de longueur, et marquer chaque unité long de l'axe, formant une grille. Pour spécifier un point particulier sur un système à deux dimensions de coordonnées, indiquer la première unité x (abscisse), suivie par l'unité de y (ordonnée) sous la forme (x, y), une paire ordonnée.

Le choix de lettres vient d'une convention, d'utiliser la dernière partie de l'alphabet pour indiquer des valeurs inconnues. En revanche, la première partie de l'alphabet a été utilisé pour désigner des valeurs connues.

Un exemple d'un point P sur le système est indiquée sur la figure 3, en utilisant la coordonnée (3,5).

L'intersection des deux axes crée quatre régions, appelées quadrants, renseignées par les chiffres romains I (+, +), II (-, +), III (-, -) et IV (+, -). Classiquement, les quadrants sont étiquetés anti-horaire à partir du coin supérieur droit ("nord") de quadrant. Dans le premier quadrant, les deux coordonnées sont positives, dans le deuxième quadrant x -coordinates sont négatifs et y -coordinates positif, dans le troisième quadrant deux coordonnées sont négatifs et dans le quatrième quadrant, x -coordinates sont positifs et y -coordinates négative ( voir tableau ci-dessous.)

Three-dimensional système de coordonnées

Figue. 4 - système tridimensionnel de coordonnées cartésiennes avec l'axe y se éloignant de l'observateur.

Figue. 5 - tridimensionnel système de coordonnées cartésiennes avec l'axe des abscisses orienté vers l'observateur.

Le coordonner surfaces des coordonnées cartésiennes (x, y, z). L'axe z est vertical et l'axe des x est surligné en vert. Ainsi, le rouge plan montre les points avec x = 1, le bleu plan montre les points avec z = 1, et le plan jaune indique les points avec y = -1. Les trois surfaces se coupent au point P (présentée comme une sphère noire) avec les coordonnées cartésiennes (1,0, -1,0, 1,0).

Le système de coordonnées cartésiennes dimensions trois fournit les trois dimensions physiques de l'espace - Longueur, largeur, hauteur et. Les figures 4 et 5 représentent deux manières communes de représenter.

Les trois axes cartésiens définissant le système sont perpendiculaires les uns aux autres. Les coordonnées pertinentes sont de la forme (x, y, z). A titre d'exemple, la figure 4 montre deux points tracés dans un système de coordonnées cartésiennes en trois dimensions: P (3,0,5) et Q (-5, -5,7). Les axes sont représentés dans un "monde coordonnées" orientation de l'axe z vers le haut.

Les x -, y -, et z -coordinates d'un point peuvent également être considérées comme les distances du plan yz, xz Plane, Plane et xy respectivement. La figure 5 montre les distances de point P des avions.

Le xy -, yz -, xz et -plans diviser l'espace en trois dimensions en huit subdivisions appelées octants, semblables aux quadrants d'espace 2D. Alors que les conventions ont été établies pour l'étiquetage des quatre quadrants du plan x - y, seul le premier octant de l'espace tridimensionnel est étiqueté. Elle contient tous les points dont x, y et z les coordonnées sont positives.

Le z -Coordonner est aussi appelé applicate.

Orientation et impartialité

Dans deux dimensions

Le règle de la main droite.

Fixation ou en choisissant l'axe des x détermine l'axe y jusqu'à direction. A savoir, l'axe des y est nécessairement le perpendiculaire à l'axe des x par le point marqué 0 sur l'axe des x. Mais il se agit d'un choix de celui des deux lignes de moitié sur la perpendiculaire à désigner comme positif et négatif qui. Chacun de ces deux choix détermine une orientation différente (également appelée chiralité) du plan cartésien.

La manière habituelle d'orientation des axes, avec le x positif selon l'axe pointant vers la droite et l'y positif selon l'axe vers le haut (et l'axe des x étant la «première» et l'axe des y la "deuxième" axe) est considéré comme le positif ou l'orientation standard, également appelé l'orientation droitier.

Un moyen mnémotechnique couramment utilisé pour définir l'orientation positive est le règle de la main droite. Plaçant une main peu fermé à droite sur le plan avec le pouce vers le haut, les doigts pointent du axe x à l'axe des y, dans un système de coordonnées orienté positivement.

L'autre façon d'orienter les axes suit la règle de la main gauche, en plaçant la main gauche sur le plan avec le pouce pointant vers le haut.

Indépendamment de la règle utilisée pour orienter les axes, la rotation du système de coordonnées permettra de préserver l'orientation. Commutation le rôle de x et y sera inverser l'orientation.

En trois dimensions

Figue. 7 - L'orientation de la main gauche est représentée sur la gauche, et le droitier à droite.

Figue. 8 - Le droitier système de coordonnées cartésiennes indiquant les plans de coordonnées.

Une fois que le x - et -axes y sont spécifiées, elles déterminent la ligne le long de laquelle l'axe z devraient mentir, mais il ya deux directions possibles sur cette ligne. Les deux systèmes possibles de coordonnées qui en résultent sont appelés «à droite» et «gauchers». L'orientation standard, où la Plane xy est horizontal et l'axe z pointe vers le haut (et le x - et l'axe y former un système de coordonnées bidimensionnelles orienté positivement dans le Plane xy si observé depuis le dessus du Plane xy ) est appelé droitiers ou positif.

Le nom dérive de la Règle de la main droite. Si le l'index de la main droite est pointé vers l'avant, la doigt du milieu repliée vers l'intérieur à un angle droit à, et le pouce placé à angle droit aux deux, les trois doigts indiquer les directions relatives du x -, y -, et z -axes dans un système droitier. Le pouce indique l'axe des x, l'index de l'axe des y et le majeur de l'axe z. Inversement, si on fait de même avec la main gauche, un des résultats du système gauchers.

Figure 7 est une tentative représentant un gauche et un système droitier coordonnées. Parce qu'un objet tridimensionnel est représenté sur le résultat écran bidimensionnel, la distorsion et l'ambiguïté. L'axe pointé vers le bas (et vers la droite) est également destinée à être orientée vers l'observateur, tandis que l'axe "milieu" est destiné à indiquer l'écart de l'observateur. Le cercle rouge est parallèle à l'Plane horizontal xy et indique une rotation de la axe des x de l'axe des y (dans les deux cas). D'où la flèche rouge passe devant l'axe des z.

Figure 8 est une autre tentative de dépeindre un système droitier coordonnées. Encore une fois, il existe une ambiguïté due à la projection du système de coordonnées à trois dimensions dans le plan. Beaucoup d'observateurs considèrent Figure 8 comme «retournement in and out» entre un convexe et un cube concave "coin". Cela correspond aux deux orientations possibles du système de coordonnées. Voir la figure comme convexe donne un système gaucher coordonnées. Ainsi, la «bonne» façon de voir Figure 8 est d'imaginer l'axe des x comme pointant vers l'observateur et donc voir un coin concave.

Représentant un vecteur dans la base standard

Un point de l'espace dans un système de coordonnées cartésiennes peut également être représenté par un vecteur, qui peut être considéré comme une flèche pointant de l'origine du système au point de coordonnées. Si les coordonnées représentent des positions spatiales (déplacements) il est courant de représenter le vecteur entre l'origine et le point d'intérêt en tant que 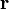. En trois dimensions, le vecteur de l'origine au point de coordonnées cartésiennes qui est parfois écrit que:

où , 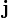Et sont vecteurs unitaires qui indiquent la même direction que la 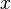, Et 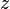axes, respectivement. Ceci est le quaternionique représentation du vecteur et a été introduit par Sir William Rowan Hamilton. Les vecteurs unitaires , 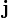Et on appelle les versors du système de coordonnées, et sont les vecteurs de la base standard en trois dimensions.

Applications

Les coordonnées cartésiennes sont souvent utilisées pour représenter deux ou trois dimensions de l'espace, mais ils peuvent également être utilisés pour représenter des quantités beaucoup d'autres (tels que masse, temps, force, etc.). Dans ce cas, les axes de coordonnées sont typiquement marquées avec d'autres (tels que des lettres m, t, F, etc.) à la place de x, y, et z. Chaque axe peut aussi avoir différentes unités de mesure qui lui sont associés (tels que kilogramme, seconde, livres, etc.). Il est également possible de définir des systèmes de coordonnées de plus de trois dimensions pour représenter les relations entre les quantités de plus de trois. Bien que quatre et espaces de dimensions supérieures sont difficiles à visualiser, l'algèbre des coordonnées cartésiennes peut être étendue assez facilement quatre ou plusieurs variables, de sorte que certains calculs impliquant de nombreuses variables peuvent être faites. (Cette sorte d'extension algébrique est ce qui est utilisé pour définir la géométrie des espaces de dimensions supérieures, qui peuvent devenir assez compliqué.) Inversement, il est souvent utile d'utiliser la géométrie des coordonnées cartésiennes en deux ou trois dimensions pour visualiser les relations algébriques entre deux ou trois (peut-être deux ou trois des nombreux) variables non-spatiales.