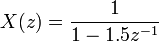La théorie du contrôle
Contexte des écoles Wikipédia
Enfants SOS ont produit une sélection d'articles de wikipedia pour les écoles depuis 2005. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .
La théorie du contrôle est une branche interdisciplinaire de l'ingénierie et des mathématiques , qui traite avec le comportement de systèmes dynamiques. La sortie souhaitée d'un système est appelé référence. Lorsque une ou plusieurs variables de sortie d'un système doivent suivre une certaine référence au fil du temps, un contrôleur manipule les entrées à un système pour obtenir l'effet désiré sur la sortie du système.
| Wikibooks a un livre sur le thème de: Systèmes de contrôle |
Vue d'ensemble
La théorie du contrôle est
- la théorie, qui traite influencer le comportement des systèmes dynamiques
- sous-champ interdisciplinaire de la science qui trouve son origine dans l'ingénierie et les mathématiques , et a évolué vers l'utilisation par les sciences sociales, comme la psychologie , la sociologie et criminologie.
Un exemple
Envisager une automobile de régulateur de vitesse, qui est un dispositif conçu pour maintenir une vitesse constante du véhicule; la vitesse de consigne ou de référence, fournies par le pilote. Le système est dans ce cas le véhicule. La sortie du système est la vitesse du véhicule, et la grandeur de commande est un moteur de position du papillon qui influence moteur sortie de couple.
Une façon simple de mettre en œuvre le régulateur de vitesse est de verrouiller la position du papillon lorsque le conducteur engage régulateur de vitesse. Cependant, sur un terrain vallonné, le véhicule ralentit en montée et accélérer descente. En fait, ne importe quel paramètre différent de ce qui a été pris au moment du design se traduira par une erreur proportionnelle à la vitesse de sortie, y compris la masse exacte du véhicule, la résistance au vent, et de la pression des pneus. Ce type de commande est appelé un contrôleur en boucle ouverte parce qu'il n'y a pas de connexion directe entre la sortie du système (le couple moteur) et les conditions réelles rencontrées; ce est-à-dire, le système ne fonctionne pas et ne peut pas compenser les forces inattendues.
Dans un système de commande en boucle fermée, un capteur surveille la sortie (la vitesse du véhicule) et alimente les données à un ordinateur qui ajuste en permanence l'entrée de commande (le gaz) que nécessaire pour que l'écart de régulation à un minimum (pour maintenir la souhaitée vitesse). Commentaires sur la façon dont le système effectue en fait permet au contrôleur (véhicule est l'ordinateur de bord) pour compenser dynamiquement pour les perturbations du système, tels que les changements dans la pente de la vitesse au sol ou le vent. Un système de contrôle de rétroaction idéale annule toutes les erreurs, atténuer efficacement les effets de toutes les forces qui peuvent ou peuvent ne pas survenir pendant le fonctionnement et produisant une réponse dans le système qui correspond parfaitement aux souhaits de l'utilisateur.
Histoire
Bien que les systèmes de contrôle de différents types remontent à l'antiquité, une analyse plus formelle du champ a commencé par une analyse de la dynamique de la régulateur centrifuge, menée par le physicien James Clerk Maxwell en 1868 intitulé On gouverneurs. Ce décrit et analysé le phénomène de la «chasse», dans lequel les retards dans le système peut conduire à une surcompensation et le comportement instable. Cela a généré une vague d'intérêt dans le sujet, au cours de laquelle le camarade de classe de Maxwell Edward John Routh généraliser les résultats de Maxwell pour la classe générale des systèmes linéaires. Indépendamment, Adolf Hurwitz analysé la stabilité du système en utilisant des équations différentielles en 1877 . Ce résultat est appelé le Théorème de Routh-Hurwitz.
Une application notable de contrôle dynamique était dans le domaine des vols habités. Les frères Wright ont fait leurs premiers vols d'essai réussis sur 17 décembre 1903 et se distinguent par leur capacité à contrôler leurs vols pour de longues périodes (plus que la capacité de produire de la portance d'une surface portante, qui était connu). Contrôle de l'avion était nécessaire pour la sécurité du vol.
Par la Seconde Guerre mondiale , la théorie du contrôle était une partie importante de systèmes de commande de tir, systèmes de guidage et de l'électronique . La course de l'espace dépend aussi sur le contrôle de l'engin spatial précis. Cependant, la théorie du contrôle a également vu une utilisation croissante dans des domaines comme l'économie .
Les gens dans les systèmes et le contrôle
De nombreuses personnalités actives et historiques faites contribution significative à contrôler la théorie, par exemple:
- Alexander Lyapunov (1857-1918) dans les années 1890 marque le début de théorie de la stabilité.
- Harold S. Black (1898-1983), a inventé le amplificateur de rétroaction négative dans les années 1930.
- Harry Nyquist (1889-1976), a développé le Critère de stabilité de Nyquist pour les systèmes de rétroaction dans les années 1930.
- Richard Bellman (1920-1984), développé programmation dynamique depuis les années 1940.
- Norbert Wiener (1894-1964) a inventé le terme Cybernétique dans les années 1940.
- John R. Ragazzini (1912-1988) introduit commande numérique et de la z transformer dans les années 1950.
Théorie du contrôle classique: le contrôleur en boucle fermée
Pour éviter les problèmes de la commande en boucle ouverte, contrôler introduit la théorie rétroaction. Une boucle fermée contrôleur utilise la rétroaction au contrôle Unis ou des sorties d'un système dynamique. Son nom vient de la voie de l'information dans le système: entrées de processus (par exemple, la tension appliquée à un moteur électrique) avoir un effet sur les sorties de processus (par exemple la vitesse ou le couple du moteur), qui est mesurée avec capteurs et traitées par le contrôleur; le résultat (le signal de commande) est utilisé comme entrée pour le processus, la fermeture de la boucle.
Contrôleurs en boucle fermée présentent les avantages suivants par rapport aux contrôleurs à boucle ouverte:
- rejet de perturbation (tels que le frottement non mesurée dans un moteur)
- performance garantie même avec les incertitudes des modèles, lorsque la structure du modèle ne correspond pas parfaitement le processus réel et les paramètres du modèle ne sont pas exactes
- processus instables peuvent être stabilisées
- une sensibilité réduite à des variations de paramètres
- performances de suivi amélioré de référence
Dans certains systèmes, en boucle fermée et en boucle ouverte de contrôle sont utilisés simultanément. Dans ces systèmes, la commande en boucle ouverte est appelée anticipation et sert à améliorer encore les performances de suivi de référence.
Une architecture de contrôleur en boucle fermée commune est le Régulateur PID.
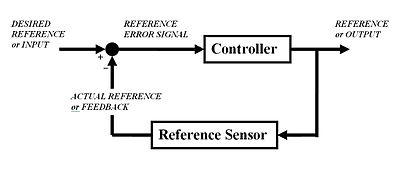
La sortie du système y (t) est renvoyée à la valeur r de référence (t), par une mesure de capteur. Le dispositif de commande C prend alors l'e d'erreur (différence) entre la référence et la sortie pour modifier les entrées u au système sous la commande P. Ceci est représenté sur la figure. Ce type de contrôleur est un contrôleur de dispositif de commande ou de la rétroaction en boucle fermée.
Cela se appelle une seule entrée-sortie unique (SISO) système de contrôle; MIMO (Multi-dire entrée-sorties multiples) systèmes, avec plus d'une entrée / sortie, sont communs. Dans de tels cas les variables sont représentés par vecteurs au lieu de simples valeurs scalaires. Pour certains systèmes à paramètres répartis les vecteurs peuvent être infinite- dimensions (typiquement fonctions).

Si nous supposons que le contrôleur C et l'usine sont P linéaire et invariant dans le temps (ex: éléments de leur fonction de transfert C (s) et P (s) ne dépend pas de temps), les systèmes ci-dessus peuvent être analysés en utilisant le Transformée de Laplace sur les variables. On obtient les relations suivantes:
Résolution Y (s) en termes de R (s) donne:
Le terme 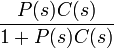 que l'on appelle la fonction de transfert du système. Le numérateur est le gain vers l'avant à partir de R à Y, et le dénominateur est un plus le gain de boucle de la boucle de rétroaction. Si
que l'on appelle la fonction de transfert du système. Le numérateur est le gain vers l'avant à partir de R à Y, et le dénominateur est un plus le gain de boucle de la boucle de rétroaction. Si  , Ce est à dire qu'il a un grand norme avec chaque valeur de s, alors Y (s) est approximativement égale à R (s). Cela implique de mettre tout simplement la référence contrôle la sortie.
, Ce est à dire qu'il a un grand norme avec chaque valeur de s, alors Y (s) est approximativement égale à R (s). Cela implique de mettre tout simplement la référence contrôle la sortie.
Sujet de la théorie du contrôle
Stabilité
Stabilité (en théorie du contrôle) signifie souvent que pour toute entrée bornée sur un montant de temps, la sortie sera également limitée. Ceci est connu comme La stabilité BIBO (voir aussi Lyapunov stabilité). Si un système est BIBO stable alors la sortie ne peut pas "sauter" (ce est à dire, devenir infinie) si l'entrée reste finie. Mathématiquement, cela signifie que pour un système linéaire causal soit stable tout le pôles de son fonction de transfert doit satisfaire à certains critères en fonction de si une analyse continue ou discrète de temps est utilisée:
- En temps continu, le Transformée de Laplace est utilisée pour obtenir la fonction de transfert. Un système est stable si les pôles de cette fonction de transfert se trouvent strictement dans la moitié gauche fermée du plan complexe . ce est à dire la partie réelle de l'ensemble des pôles est inférieur à zéro).
OU
- En temps discret du Z transformée est utilisée. Un système est stable si les pôles de cette fonction de transfert se trouvent à l'intérieur du strictyly cercle unité. ce est à dire l'amplitude des pôles est inférieur à un).
Lorsque les conditions ci-dessus sont appropriées satisfait un système est dit être asymptotiquement stable: les variables d'un système de commande diminuent toujours asymptotiquement stable à partir de sa valeur initiale et ne montrent pas oscillations permanentes. Oscillations permanentes se produire lorsque un pôle a une partie réelle exactement égale à zéro (dans le cas de temps continu) ou un module égale à une (dans le cas de temps discret). Si une réponse du système stable tout simplement ne se désintègre, ni se développe au fil du temps, et n'a pas d'oscillations, il est marginalement stable: dans ce cas, la fonction de transfert du système a des pôles non répétées à l'origine de plan complexe (ce est à dire leur composante réelle et complexe est nulle dans le cas de temps continu). Oscillations sont présents lorsque pôles avec partie réelle égale à zéro ont une partie imaginaire est pas égal à zéro.
Les différences entre les deux cas ne sont pas une contradiction. La transformation de Laplace est en coordonnées cartésiennes et de la Z-transform est en coordonnées circulaires , et il peut être démontré que
- la partie négative réel dans le domaine de Laplace peut mapper sur l'intérieur du cercle unité
- la partie positive-réel dans le domaine de Laplace peut mapper sur l'extérieur du cercle unité
Si un système en question a une réponse impulsionnelle
puis le Z-transform (voir cet exemple), est donnée par
qui a un pole 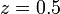 (Zéro partie imaginaire). Ce système est BIBO (asymptotiquement) stable puisque le pôle est à l'intérieur du cercle unité.
(Zéro partie imaginaire). Ce système est BIBO (asymptotiquement) stable puisque le pôle est à l'intérieur du cercle unité.
Cependant, si la réponse impulsionnelle est
alors le Z-transform est
qui a un pôle à 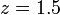 et ne est pas BIBO stable puisque le pôle a un module strictement supérieur à un.
et ne est pas BIBO stable puisque le pôle a un module strictement supérieur à un.
De nombreux outils existent pour l'analyse des pôles d'un système. Il se agit notamment des systèmes graphiques comme le lieu des racines, parcelles de Bode ou Parcelles de Nyquist.
Contrôlabilité et observabilité
Contrôlabilité et observabilité sont principales questions à l'analyse d'un système avant de décider de la meilleure stratégie de lutte à appliquer, ou se il est même possible de contrôler ou à stabiliser le système. Contrôlabilité est liée à la possibilité de forcer le système dans un état particulier en utilisant un signal de contrôle approprié. Si un Etat ne est pas contrôlable, aucun signal ne sera jamais en mesure de contrôler l'état. Si un Etat ne est pas contrôlable, mais sa dynamique sont stables, alors l'état où il est appelé stabilisable. Observabilité place est liée à la possibilité d'une "observation", par des mesures de sortie, l'état d'un système. Si un Etat ne est pas observable, le contrôleur ne sera jamais en mesure de déterminer le comportement d'un Etat non observables et donc ne peut pas l'utiliser pour stabiliser le système. Toutefois, même à l'état de stabilisabilité ci-dessus, si un État ne peut pas être observé il pourrait encore être détectable.
D'un point de vue géométrique, en regardant les états de chaque variable du système à être contrôlé, tous les «mauvais» état de ces variables doit être contrôlable et observable pour assurer un bon comportement dans le système en boucle fermée. Ce est, si l'une des valeurs propres du système ne est pas à la fois contrôlable et observable, cette partie de la dynamique restera intacte dans le système en boucle fermée. Si une telle valeur propre ne est pas stable, la dynamique de cette valeur propre sera présent dans le système en boucle fermée qui sera donc instable. Pôles non observables ne sont pas présents dans la fonction de transfert réalisation d'une représentation d'état, ce est pourquoi parfois ce dernier est préféré dans l'analyse des systèmes dynamiques.
Les solutions aux problèmes de système incontrôlable ou inobservable comprennent l'ajout de capteurs et actionneurs.
Spécifications de contrôle
Plusieurs stratégies de contrôle différents ont été mis au point dans les dernières années. Celles-ci varient de celles extrêmement générales ( Régulateur PID), à d'autres consacré à mêmes catégories particulières de systèmes (en particulier robotique ou avions régulateur de vitesse).
Un problème de contrôle peut avoir plusieurs spécifications. Stabilité, bien sûr, est toujours présent: le contrôleur doit se assurer que le système en boucle fermée est stable, indépendamment de la stabilité en boucle ouverte. Un mauvais choix de contrôleur peut même aggraver la stabilité du système en boucle ouverte, qui doit normalement être évitée. Parfois, il serait souhaitable d'obtenir une dynamique particulière dans la boucle fermée: ce est à dire que les pôles ont ![Re [\ lambda] <- \ overline {\ lambda}](../../images/190/19048.png) Où
Où  est une valeur fixe strictement supérieure à zéro, au lieu de simplement demander que
est une valeur fixe strictement supérieure à zéro, au lieu de simplement demander que ![Re [\ lambda] <0](../../images/190/19050.png) .
.
Une autre spécification typique est le rejet d'une perturbation de l'étape; comprenant un intégrateur de la chaîne en boucle ouverte (ce est à dire juste avant le système sous contrôle) réalise facilement cela. D'autres classes de perturbations besoin de différents types de sous-systèmes pour être inclus.
Autres caractéristiques «classiques» de la théorie de contrôle considèrent le temps de réponse du système en boucle fermée: il se agit notamment de la temps de montée (le temps requis par le système de contrôle pour atteindre la valeur désirée après une perturbation), le pic dépassement (la plus haute valeur atteinte par la réponse avant d'atteindre la valeur souhaitée) et autres ( temps de stabilisation, quart de pourriture). les spécifications de domaine de fréquence sont généralement liés à robustesse (voir après).
Évaluations de performance modernes utilisent une variation d'erreur de suivi intégré (IAE, ISA, CQI).
l'identification du modèle et la robustesse
Un système de contrôle doit toujours avoir une certaine propriété de robustesse. Un correcteur robuste est tel que ses propriétés ne changent pas beaucoup si elle est appliquée à un système légèrement différent de celui mathématique utilisé pour sa synthèse. Cette spécification est important: aucun système physique réel se comporte vraiment comme la série d'équations différentielles utilisées pour représenter mathématiquement. Typiquement, un modèle mathématique simple est choisi pour simplifier les calculs, sinon les vrais dynamique du système peuvent être si compliqué que d'un modèle complet est impossible.
Identification du système
Le processus de détermination des équations qui régissent la dynamique du modèle est appelé identification de système. Cela peut se faire hors ligne: par exemple, l'exécution d'une série de mesures à partir de laquelle calculer un modèle mathématique approchée, généralement son fonction de transfert ou une matrice. Cette identification de la sortie, cependant, ne peut pas tenir compte de la dynamique non observables. Parfois, le modèle est construit directement à partir des équations physiques connues: par exemple, dans le cas d'un système masse-ressort-amortisseur nous savons que 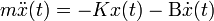 . Même en supposant que le modèle «complet» est utilisé dans la conception du contrôleur, tous les paramètres inclus dans ces équations (appelés «paramètres nominaux") ne sont jamais connue avec une précision absolue; le système de contrôle devra comporter correctement même lorsque vous êtes connecté à un système physique avec les vraies valeurs de paramètres loin de nominal.
. Même en supposant que le modèle «complet» est utilisé dans la conception du contrôleur, tous les paramètres inclus dans ces équations (appelés «paramètres nominaux") ne sont jamais connue avec une précision absolue; le système de contrôle devra comporter correctement même lorsque vous êtes connecté à un système physique avec les vraies valeurs de paramètres loin de nominal.
Certaines techniques de contrôle avancées incluent un processus d'identification "on-line" (voir plus loin). Les paramètres du modèle sont calculés ("identifié"), tandis que le dispositif de commande lui-même est en cours d'exécution: de cette manière, si une variation drastique des paramètres se ensuit (par exemple, si le bras de robot libère un poids), le contrôleur se ajustera en conséquence afin d'assurer la bonne exécution.
Analyse
L'analyse de la robustesse d'un système de contrôle de SISO peut être effectuée dans le domaine des fréquences, en tenant compte de la fonction de transfert du système et l'utilisation Nyquist et diagrammes de Bode. Les sujets traités comprennent gain et la phase de marge et la marge d'amplitude. Pour MIMO et, en général des systèmes de contrôle, plus complexes, il faut examiner les résultats théoriques élaborés pour chaque technique de contrôle (voir la section suivante): par exemple, si des qualités particulières de robustesse sont nécessaires, l'ingénieur doit passer son attention sur une technique de contrôle de les inclure dans ses propriétés.
Contraintes
Un problème de robustesse particulière est l'exigence d'un système de contrôle pour effectuer correctement en présence de contraintes sur les intrants et de l'Etat. Dans le monde physique chaque signal est limitée. Il peut arriver qu'un contrôleur envoie des signaux de commande qui ne peuvent pas être suivies par le système physique: par exemple, en essayant de faire tourner une valve à une vitesse excessive. Cela peut produire un comportement indésirable du système en boucle fermée, ou même briser actionneurs ou d'autres sous-systèmes. Techniques de contrôle spécifiques sont disponibles pour résoudre le problème: modéliser commande prédictive (voir plus loin), et anti-vent en place des systèmes. Ce dernier est constitué d'un bloc de commande supplémentaire qui se assure que le signal de commande ne dépasse un seuil donné.
Stratégies de contrôle principales
Chaque système de contrôle doit garantir abord la stabilité du comportement en boucle fermée. Pour systèmes linéaires, ceci peut être obtenu en plaçant directement les pôles. Les systèmes de contrôle non linéaires utilisent des théories particulières (normalement basés sur La théorie de Aleksandr Lyapunov) pour assurer la stabilité, sans égard à la dynamique interne du système. La possibilité de remplir des spécifications différentes varie du modèle considéré et de la stratégie de contrôle choisi. Voici une liste sommaire des principales techniques de contrôle se affiche:
Contrôle classique
Le Régulateur PID est probablement la conception la plus utilisée asservissement la, étant la plus simple. "PID" signifie proportionnelle, intégrale et dérivée, en se référant aux trois conditions opérantes sur le signal d'erreur pour produire un signal de commande. Si u (t) est le signal de commande envoyé au système, y (t) est la sortie mesurée et r (t) est la sortie désirée, et l'erreur de suivi  , Un régulateur PID a la forme générale
, Un régulateur PID a la forme générale
Les dynamiques désirées en boucle fermée est obtenu en ajustant les trois paramètres  ,
,  et
et  , Souvent de manière itérative par "tuning" et sans connaissances spécifiques d'un modèle de plante. La stabilité peut souvent être assurée en utilisant uniquement le terme proportionnel. Le terme intégral permet le rejet d'une perturbation de l'étape (souvent une spécification en frappant contrôle de processus). Le terme dérivé est utilisé pour fournir d'amortissement ou de façonnage de la réponse. Contrôleurs PID sont la classe la plus bien établi des systèmes de contrôle: cependant, ils ne peuvent pas être utilisés dans plusieurs cas plus compliqués, surtout si les systèmes MIMO sont considérés.
, Souvent de manière itérative par "tuning" et sans connaissances spécifiques d'un modèle de plante. La stabilité peut souvent être assurée en utilisant uniquement le terme proportionnel. Le terme intégral permet le rejet d'une perturbation de l'étape (souvent une spécification en frappant contrôle de processus). Le terme dérivé est utilisé pour fournir d'amortissement ou de façonnage de la réponse. Contrôleurs PID sont la classe la plus bien établi des systèmes de contrôle: cependant, ils ne peuvent pas être utilisés dans plusieurs cas plus compliqués, surtout si les systèmes MIMO sont considérés.
Contrôle linéaire
Pour les systèmes MIMO, placement de pôles peut être réalisé en utilisant un mathématiquement Etat représentation spatiale du système en boucle ouverte et le calcul d'une matrice de contre-réaction attribution pôles dans les positions souhaitées. Dans les systèmes complexes cela peut nécessiter des capacités de calcul assisté par ordinateur, et ne peut pas toujours assurer la robustesse. En outre, tous les Etats du système ne sont pas en observateurs mesurées et si générale doivent être inclus et intégrés dans la conception de placement de pôles.
Commande non linéaire
Processus dans les industries comme la robotique et de la industrie aérospatiale ont généralement forte dynamique non-linéaire. Dans la théorie de contrôle, il est parfois possible de linéariser ces classes de systèmes et appliquer des techniques linéaires: mais dans de nombreux cas, il peut être nécessaire de concevoir des théories à gratter permettant le contrôle des systèmes non linéaires. Il se agit, par exemple, rétroaction linéarisation, backstepping, commande coulissante de mode, le contrôle de linéarisation trajectoire normalement prendre avantage des résultats repose sur Théorie. Lyapunov de la géométrie différentielle a été largement utilisé comme un outil pour la généralisation des concepts de contrôle linéaires bien connues pour le cas non-linéaire, ainsi que de montrer les subtilités qui font ce un problème plus difficile.
Contrôle optimal
Commande optimale est une technique de contrôle particulier dans lequel le signal de commande permet d'optimiser un certain «indice de coût»: par exemple, dans le cas d'un satellite, les axes des jets nécessaires pour l'amener à la trajectoire désirée qui consomme le moins de combustible. Deux méthodes de conception optimale de contrôle ont été largement utilisés dans des applications industrielles, comme il a été montré qu'elles peuvent garantir la stabilité en boucle fermée. Ceux-ci sont Modèle Predictive Control (MPC) et Commande LQG (LQG). Le premier peut prendre plus explicitement en compte les contraintes sur les signaux dans le système, qui est un élément important dans de nombreux processus industriels. Cependant, la structure "de la commande optimale" dans les PPM ne est qu'un moyen pour atteindre un tel résultat, car il ne optimise pas un véritable indice de performance du système de contrôle en boucle fermée. Ensemble avec les contrôleurs PID, systèmes MPC sont la technique de contrôle le plus largement utilisé dans contrôle de processus.
Contrôle adaptatif
Contrôle adaptatif utilise l'identification en ligne des paramètres du procédé, ou la modification des gains de contrôleur, de façon à obtenir des propriétés de robustesse fortes. Adaptive contrôles ont été appliquées pour la première fois dans la industrie aérospatiale dans le Années 1950, et ont trouvé un succès particulier dans ce domaine.
Commande intelligente
L'utilisation de contrôle intelligent diverses approches comme l'informatique AI réseaux de neurones, Probabilité bayésienne, logique floue, l'apprentissage machine, calcul évolutif et algorithmes génétiques pour contrôler un système dynamique
Contrôle hiérarchique
Un système de contrôle hiérarchique est une forme de Système de contrôle dans lequel un ensemble de dispositifs et de logiciels d'administration est disposé dans un hiérarchique arbre. Lorsque les maillons de l'arbre sont mis en oeuvre par un réseau informatique, alors que le système de contrôle hiérarchique est aussi une forme de Système de contrôle en réseau.
Littérature
- Christopher Kilian (2005). Technologie de contrôle moderne. Thompson apprentissage Delmar. ISBN 1-4018-5806-6.
- Vannevar Bush (1929). Analyse circuit opérationnel. John Wiley and Sons, Inc ..
- Robert F. Stengel (1994). Contrôle optimal et estimation. Dover Publications. ISBN 0-486-68200-5, ISBN-13: 978-0-486-68200-6.
- Franklin et al. (2002). Commentaires contrôle de systèmes dynamiques (4 ed.). New Jersey: Prentice Hall. ISBN 0-13-032393-4.
- Joseph L. Hellerstein, Dawn M. Tilbury, et Sujay Parekh (2004). Commentaires de contrôle des systèmes informatiques. John Wiley and Sons. ISBN 0-47-126637-X, ISBN-13: 978-0-471-26637-2.
- Système dynamique et Anthony J. Pritchard (2005) Systèmes mathématiques Théorie I -. Modélisation, Analyse spatiale État, de stabilité et de robustesse. Springer. ISBN 0-978-3-540-44125-0.
- Sontag, Eduardo (1998) la théorie du contrôle mathématique:. Systèmes de dimension finie déterministes. Deuxième Édition. Springer. ISBN 0-387-984895.
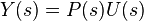

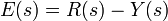

![\ x [n] = 0,5 ^ n u [n]](../../images/190/19042.png)
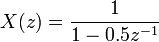
![\ x [n] = 1,5 ^ n u [n]](../../images/190/19045.png)