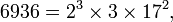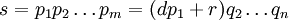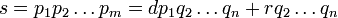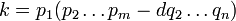Théorème fondamental de l'arithmétique
Saviez-vous ...
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Les enfants SOS est le plus grand don de charité du monde enfants orphelins et abandonnés la chance de la vie familiale.
Dans la théorie des nombres , le théorème fondamental de l'arithmétique (ou uniques-prime-factorisation théorème) stipule que chaque nombre naturel supérieur à 1 peut être écrit comme un produit unique de nombres premiers . Par exemple,
Il n'y a pas d'autres possibles factorisations de 6936 ou 1200 dans les nombres premiers. La représentation ci-dessus se effondre répété facteurs premiers en pouvoirs pour faciliter l'identification. Parce que la multiplication est commutative et associative , l'ordre des facteurs ne est pas pertinent et le plus souvent écrite, du moins au plus grand.
De nombreux auteurs prennent les nombres naturels à commencer par 0, qui n'a pas de facteurs premiers. Ainsi Théorème 1 de Hardy & Wright (1979) prend la forme, "Chaque entier positif, sauf une, est un produit de nombres premiers", et le théorème 2 (leur «fondamentales») affirme unicité. Le numéro 1 ne est pas se amorcer, mais puisque ce est le produit d'aucun chiffre, il est souvent pratique de l'inclure dans le théorème par le vide règle du produit. (Voir, par exemple, Calcul du pgcd .)
Hardy & Wright définissent un nombre anormal d'être un nombre hypothétique qui ne possède pas une factorisation unique. Ils prouvent le théorème fondamental de l'arithmétique en prouvant qu'il ne existe pas un nombre anormal.
Applications
Le théorème fondamental de l'arithmétique établit l'importance des nombres premiers. Les nombres premiers sont les blocs de construction de base de tout nombre entier positif, en ce sens que chaque entier positif peut être construit à partir du produit de nombres premiers avec une construction unique. Trouver la factorisation d'un entier permet dérivation de tous ses diviseurs, à la fois premiers et non-prime.
Par exemple, au-dessus de la factorisation de 6936 montre que ne importe quel diviseur positif de 6936 doit avoir la forme  Où
Où  prend l'une des quatre valeurs dans {0, 1, 2, 3}, où
prend l'une des quatre valeurs dans {0, 1, 2, 3}, où  prend l'une des deux valeurs dans {0, 1}, et où
prend l'une des deux valeurs dans {0, 1}, et où  prend l'une des valeurs 3 dans {0, 1, 2}. En multipliant le nombre d'options indépendantes ensemble produit un total de
prend l'une des valeurs 3 dans {0, 1, 2}. En multipliant le nombre d'options indépendantes ensemble produit un total de 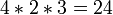 diviseurs positifs.
diviseurs positifs.
Une fois que les facteurs premiers de deux nombres sont connus, leur plus grand commun diviseur et moins commun multiple peut être trouvé rapidement. Par exemple, à partir de ce qui précède, il est montré que le plus grand commun diviseur de 6936 et 1200 est 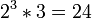 . Toutefois, si les facteurs premiers ne sont pas connus, l'utilisation de la Euclidienne algorithme nécessite généralement beaucoup moins de calculs que l'affacturage les deux numéros.
. Toutefois, si les facteurs premiers ne sont pas connus, l'utilisation de la Euclidienne algorithme nécessite généralement beaucoup moins de calculs que l'affacturage les deux numéros.
Le théorème fondamental garantit que additif et multiplicatif fonctions arithmétiques sont complètement déterminées par leurs valeurs sur les pouvoirs des nombres premiers.
Preuve
Le théorème était pratiquement prouvé par Euclide , mais la première preuve complète et correcte se trouve dans le Disquisitiones Arithmeticae par Carl Friedrich Gauss . Il peut être important de noter que les Egyptiens aiment Ahmès utilisé aspects pratiques de la tôt affacturage, et plus petit commun multiple, du théorème fondamental de l'arithmétique permettant une longue tradition de développer, formalisée par Euclide, et rigoureusement prouvée par Gauss.
Bien qu'à première vue le théorème semble «évident», il ne tient pas dans les systèmes numériques plus générales, y compris de nombreux anneaux de entiers algébriques. Ce fut d'abord fait remarquer par Ernst Kummer en 1843, dans son ouvrage sur le dernier théorème de Fermat . La reconnaissance de cet échec est l'un des premiers développements dans théorie algébrique des nombres.
La preuve d'Euclid
La preuve consiste en deux étapes. Dans la première étape chaque nombre se avère être un produit de zéro ou plusieurs nombres premiers. Dans le second, la preuve montre que les deux représentations peuvent être unifiées en une seule représentation.
Numéros de composites non-prime
Supposons qu'il y ait un nombre entier positif qui ne peut être écrit comme un produit de nombres premiers. Ensuite, il doit y avoir un plus petit nombre aussi (voir bien-commande): que ce soit n. Ce nombre n ne peut pas être 1, en raison de la Convention vide-produit ci-dessus. Il ne peut pas être un nombre premier soit, puisque tout nombre premier est un produit d'une seule écoute, lui-même. Donc, il doit être un nombre composé. Ainsi
- n = ab
où a et b sont des entiers positifs plus petits que n. Puisque n est le plus petit nombre qui ne peut être écrit comme un produit de nombres premiers, a et b peuvent être écrites comme des produits de nombres premiers. Mais alors
- n = ab
peut être écrit comme un produit de nombres premiers, ainsi, un la preuve par l'absurde. C'est un minime contre-argument.
Méthode de descente infinie
Une preuve de l'unicité de la décomposition en facteurs premiers d'un utilisations entières données descente infinie: Supposons qu'un certain entier peut être écrit comme (au moins) deux différents produits de nombres premiers: alors il doit exister un petit entier  avec une telle propriété. Notons ces deux factorisations de
avec une telle propriété. Notons ces deux factorisations de  comme
comme 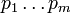 et
et  , Tel que
, Tel que  .
.
Aucun 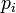 (Avec
(Avec 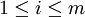 ) Peut être égale à ne importe quel
) Peut être égale à ne importe quel 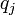 (Avec
(Avec  ), Car il y aurait autrement un entier plus petit factorisable de deux façons (en éliminant les facteurs premiers communs dans les deux produits), en violation de l'hypothèse ci-dessus. Maintenant, on peut supposer sans perte de généralité que
), Car il y aurait autrement un entier plus petit factorisable de deux façons (en éliminant les facteurs premiers communs dans les deux produits), en violation de l'hypothèse ci-dessus. Maintenant, on peut supposer sans perte de généralité que  est un facteur premier plus petit que ne importe quel
est un facteur premier plus petit que ne importe quel 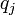 (Avec
(Avec  ). Laisser
). Laisser 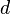 le quotient et
le quotient et  la reste de la division
la reste de la division  par
par  . Par le algorithme de division
. Par le algorithme de division 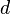 et
et  sont garantis être entiers tels que
sont garantis être entiers tels que  et
et  . Notez que
. Notez que  ne peut pas être
ne peut pas être  , Car ce serait faire
, Car ce serait faire  un multiple de
un multiple de  et pas premier. Aussi
et pas premier. Aussi 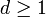 Car
Car  est supérieur à
est supérieur à  .
.
Substituant dans des  dans la définition initiale des
dans la définition initiale des  ci-dessus,
ci-dessus,
Par distributivité:
Définir un nouvel entier 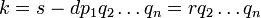 . Depuis
. Depuis 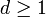 , Il est clair que
, Il est clair que 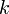 doit être inférieure à
doit être inférieure à  . Et puisque
. Et puisque  ,
, 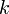 doit être positif. D'après la définition de
doit être positif. D'après la définition de 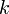 Il se ensuit que:
Il se ensuit que:
et par factorisation  :
:
Il ya donc une factorisation première 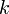 qui comprend
qui comprend  . Mais il est également vrai que
. Mais il est également vrai que
Depuis  ,
,  ne peut pas être un facteur premier de
ne peut pas être un facteur premier de  . Ainsi, en combinant les facteurs premiers de
. Ainsi, en combinant les facteurs premiers de  avec
avec 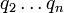 Il est également possible de construire une factorisation de
Il est également possible de construire une factorisation de 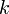 qui ne comprend pas
qui ne comprend pas  . Donc
. Donc 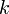 a deux facteurs premiers différents, contredisant l'hypothèse originale qui
a deux facteurs premiers différents, contredisant l'hypothèse originale qui  est le plus petit entier factorisable en plus d'une façon. Ainsi, l'hypothèse de départ doit être fausse.
est le plus petit entier factorisable en plus d'une façon. Ainsi, l'hypothèse de départ doit être fausse.