La théorie des nombres

La théorie des nombres est la branche de mathématiques pures concernées avec les propriétés des nombres en général, et des entiers en particulier, ainsi que les classes plus larges de problèmes qui découlent de leur étude.

La théorie des nombres peut être subdivisé en plusieurs champs, selon les méthodes utilisées et le type de questions étudiées. (Voir la liste de sujets de la théorie des nombres.)

Le terme « arithmétique »est également utilisé pour faire référence à la théorie des nombres. Ce est un terme un peu plus âgés, qui ne est plus aussi populaire qu'elle l'était autrefois. La théorie des nombres que l'on appelait l'arithmétique plus élevée, mais cela aussi est en baisse hors d'usage. Néanmoins, il apparaît toujours dans les noms de domaines des mathématiques ( fonctions arithmétiques, arithmétique des courbes elliptiques, théorème fondamental de l'arithmétique ). Ce sens de l'arithmétique terme ne doit pas être confondue soit avec l'arithmétique élémentaire , ou avec la branche de la logique dont les études Peano comme système formel. mathématiciens travaillant dans le domaine de la théorie des nombres sont appelés théoriciens des nombres.

Lorsque vous organisez les nombres naturels dans une spirale et en insistant sur les nombres premiers, un modèle entièrement expliqué intrigante et non est observée, appelée Spirale d'Ulam.

Les champs

Théorie élémentaire des nombres

En théorie élémentaire des nombres, entiers sont étudiées sans l'utilisation de techniques d'autres domaines mathématiques. Questions de la divisibilité , utilisent de la Algorithme d'Euclide pour calculer plus grands communs diviseurs , factorisations entier en nombres premiers , enquête sur les nombres parfaits et congruences appartiennent ici. Plusieurs découvertes importantes de ce domaine sont Le petit théorème de Fermat, Le théorème d'Euler, le Théorème du reste chinois et la loi de réciprocité quadratique. Les propriétés de fonctions multiplicatives comme le Fonction de Möbius et La fonction φ d'Euler, séquences entières, factorielles , et les nombres de Fibonacci tous entrent également dans ce domaine.

Beaucoup de questions en théorie des nombres peuvent être exprimés en termes de théorie des nombres élémentaires, mais ils peuvent exiger une attention très profond et de nouvelles approches en dehors du domaine de la théorie élémentaire des nombres à résoudre. Les exemples incluent:

• La conjecture de Goldbach concernant l'expression de nombres pairs comme somme de deux nombres premiers.
• Théorème de Catalan (maintenant Le théorème de Mihailescu) concernant les pouvoirs entiers successifs.
• Le conjecture des nombres premiers jumeaux à propos de l'infinitude de paires premiers.
• Le Collatz conjectures concernant une itération simple.
• Le dernier théorème de Fermat (déclaré en 1637, mais pas prouvé jusqu'en 1994) concernant l'impossibilité de trouver entiers non nuls x, y, z tels que pour un entier n supérieur à 2.

La théorie de la Équations diophantiennes a même été montré pour être indécidable (voir Dixième problème de Hilbert).

Théorie analytique des nombres

Théorie analytique des nombres emploie le mécanisme de calcul et analyse complexe de se attaquer à des questions sur des nombres entiers. Le théorème des nombres premiers (VCN) et la connexes Hypothèse de Riemann sont des exemples. Le problème de Waring (représentant un nombre entier donné comme une somme de carrés, cubes, etc.), la conjecture des nombres premiers jumeaux (trouver une infinité de paires de premier choix avec la différence 2) et la conjecture de Goldbach (écrit entiers pairs comme somme de deux nombres premiers) sont attaqués avec des méthodes analytiques ainsi. Les preuves de la transcendance de constantes mathématiques, comme π ou e, sont également classés comme la théorie analytique des nombres. Alors que des déclarations sur nombres transcendants peuvent sembler être retiré de l'étude des nombres entiers, ils étudient vraiment les valeurs possibles de polynômes à coefficients entiers évalués à, disons, e; ils sont aussi étroitement liées au domaine de la Approximation diophantienne, où on étudie «comment bien" un nombre réel donné peut être approchée par une rationnelle une.

Théorie algébrique des nombres

En théorie algébrique des nombres, le concept d'un certain nombre est étendu au nombres algébriques qui sont racines de polynômes à rationnels coefficients. Ces domaines contiennent des éléments analogues à des nombres entiers, ce que l'on appelle entiers algébriques. Dans ce cadre, les caractéristiques familières des nombres entiers (par exemple de factorisation uniques) ne sont pas tenus. La vertu de la machinerie employed- théorie de Galois , cohomologie des groupes, la théorie du corps de classes, représentations de groupe et L-fonctions est qu'elle permet de récupérer cet ordre en partie pour cette nouvelle classe de nombres.

Beaucoup nombre des questions théoriques sont mieux attaqués par les étudiant modulo p pour tous les nombres premiers p (voir corps finis). Ceci est appelé la localisation et elle conduit à la construction de la nombres p-adiques; ce domaine d'étude est appelé analyse locale et il découle de la théorie algébrique des nombres.

La théorie des nombres géométrique

La théorie des nombres géométrique (traditionnellement appelé le géométrie des nombres) intègre certains concepts géométriques de base, tels que les réseaux, dans les questions numériques théorie. Il commence par Le théorème de Minkowski points de réseau dans convexe fixe, et conduit à des épreuves de base du caractère fini du numéro de classe et Unité théorème de Dirichlet, deux théorèmes fondamentaux en théorie algébrique des nombres.

La théorie des nombres combinatoire

Combinatoires théorie des nombres traite de nombre théorique problèmes qui impliquent combinatoires idées dans leurs formulations ou solutions. Paul Erdős est le principal fondateur de cette branche de la théorie des nombres. Sujets typiques incluent Système de revêtement, problèmes à somme nulle, divers sumsets restreintes, et progressions arithmétiques dans un ensemble de nombres entiers. Méthodes algébriques ou analytiques sont puissants dans ce domaine.

Théorie algorithmique des nombres

Théorie algorithmique des nombres étudie algorithmes pertinents en théorie des nombres. Algorithmes rapides pour Premier test et factorisation d'entiers ont des applications importantes dans la cryptographie .

Histoire

La théorie des nombres védique

Mathématiciens dans l'Inde se sont intéressés à trouver des solutions intégrales de Équations diophantiennes depuis le Époque védique. L'utilisation géométrique première des équations diophantiennes peut être retracée à la Sulba soutras, qui ont été écrit entre le 8e et 6e siècles avant JC. Baudhayana (c. 800 BC) a trouvé deux ensembles de solutions intégrales positifs à un ensemble d'équations diophantiennes simultanées, et également utilisé des équations diophantiennes simultanées avec jusqu'à quatre inconnues. Apastamba (c. 600 BC) utilisé équations diophantiennes simultanées avec jusqu'à cinq inconnues.

La théorie des nombres Jaina

En Inde, Jaina mathématiciens ont développé la théorie systématique première des numéros à partir du 4ème siècle avant JC au 2ème siècle de notre ère. (C. 400 BC) Le texte Jaina Surya Prajinapti classe tous les numéros en trois ensembles: énumérables, innombrables et infinis. Chacun de ces a été subdivisée en trois ordres:

• Enumerable moins, intermédiaire et élevé.
• Innombrables: presque innombrables, vraiment innombrables et innombrablement innombrables.
• Infini: presque infinie, véritablement infini, infiniment infinie.

Les jaïns ont été les premiers à rejeter l'idée que tous les infinis étaient les mêmes ou égal. Ils ont reconnu cinq types différents de l'infini: infinies dans une et deux directions (une dimension), infinie dans la zone (deux dimensions), infini partout (trois dimensions), et infini perpétuellement (nombre infini de dimensions).

Le plus dénombrable nombre N de la jaïns correspond au concept moderne de aleph-null (Le nombre cardinal de l'ensemble infini de nombres entiers 1, 2, ...), le plus petit cardinal Numéro transfinite. Le jaïns également défini tout un système de nombres cardinaux transfinis, dont est la plus petite.

Dans le travail Jaina sur la théorie des ensembles , deux types de base de nombres transfinis sont distingués. Sur la fois physique et motifs ontologiques, une distinction a été faite entre asmkhyata et ananata, entre infinis rigide bornées et vaguement bornées.

La théorie des nombres grec

La théorie des nombres était une étude préférée parmi les Mathématiciens grecs de l'époque hellénistique tardive (3e siècle) à Alexandrie , en Egypte , qui étaient au courant de la Concept de l'équation diophantienne dans de nombreux cas particuliers. Le premier mathématicien grec pour étudier ces équations était Diophante.

Diophante aussi regardé une méthode de trouver des solutions entières de linéaire équations indéterminées, des équations qui ne ont pas suffisamment d'informations pour produire un seul ensemble discret de réponses. L'équation est une telle équation. Diophante découvert que de nombreuses équations indéterminées peuvent être réduites à une forme où une certaine catégorie de réponses est connu même si une réponse ne est pas spécifique.

La théorie des nombres classique indienne

Équations diophantiennes ont été largement étudiés par les mathématiciens dans l'Inde médiévale, qui ont été les premiers à étudier systématiquement les méthodes pour la détermination des solutions intégrales d'équations diophantiennes. Aryabhata (499) a donné la première description explicite de la solution intégrale générale de l'équation linéaire diophantienne une 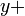b c, qui se produit dans son texte Aryabhatiya. Cet algorithme de kuttaka est considérée comme l'une des contributions les plus importantes de Aryabhata en mathématiques pures, qui ont trouvé des solutions aux équations diophantiennes au moyen de fractions continues. La technique a été appliquée par Aryabhata pour donner des solutions intégrales de simulataneous équations diophantiennes linéaires, un problème avec des applications importantes dans l'astronomie. Il a également trouvé la solution générale à la indéterminée équation linéaire en utilisant cette méthode.

Brahmagupta en 628 manipulé équations diophantiennes plus difficiles. Il a utilisé le chakravala méthode pour résoudre quadratiques équations diophantiennes, y compris les formulaires de L'équation de Pell, comme . Son Brahma Sphuta Siddhanta a été traduit en arabe en 773 et a ensuite été traduit en latin en 1126. L'équation a ensuite été posé comme un problème en 1657 par le Français mathématicien Pierre de Fermat . La solution générale de cette forme particulière de l'équation de Pell a été trouvé plus de 70 ans plus tard par Leonhard Euler , tandis que la solution générale de l'équation de Pell a été trouvé plus de 100 ans plus tard par Joseph Louis Lagrange dans il ya 1767. Pendant ce temps, de nombreux siècles, la solution générale de l'équation de Pell a été enregistré par Bhaskara II en 1150, en utilisant une version modifiée de la méthode chakravala de Brahmagupta, dont il est également utilisé pour trouver la solution générale à d'autres équations du second degré pour une période indéterminée et les équations diophantiennes quadratiques. La méthode chakravala de Bhaskara pour trouver la solution générale de l'équation de Pell était beaucoup plus simple que la méthode utilisée par Lagrange plus de 600 ans plus tard. Bhaskara également trouvé des solutions à d'autres quadratique indéterminée, cubique, quartique, et d'ordre supérieur polynômes équations. Narayana Pandit encore améliorée sur la méthode chakravala et trouvé des solutions plus générales à d'autres quadratique indéterminée et d'ordre supérieur équations polynomiales.

La théorie des nombres islamique

Du 9ème siècle, Mathématiques islamiques avaient un vif intérêt pour la théorie des nombres. Le premier de ces mathématiciens était Thabit ibn Qurra, qui a découvert un algorithme qui a permis de paires nombres amiables se trouvent, soit deux des nombres tels que chacun d'eux est la somme des diviseurs de l'autre. Au 10ème siècle, Al-Baghdadi regarda une légère variante de la méthode de Thabit ibn Qurra.

Au 10ème siècle, al-Haitham semble avoir été le premier à tenter de classer tous les même nombres parfaits (numéros égal à la somme de leurs diviseurs propres) que ceux de la forme où 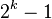est premier. Al-Haytham est également la première personne à déclarer Théorème de Wilson, à savoir que si p est premier alors 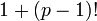est divisible par 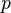. On ne sait pas se il savait comment prouver ce résultat. Il est appelé le théorème de Wilson en raison d'un commentaire fait par Edward Waring en 1770 que John Wilson avait remarqué le résultat. Il ne existe aucune preuve que John Wilson savait comment le prouver et très certainement Waring n'a pas fait. Lagrange a donné la première preuve en 1771.

Nombres amiables ont joué un grand rôle dans les mathématiques islamiques. Au 13ème siècle, Mathématicien persan Al-Farisi a donné une nouvelle preuve du théorème de Thabit ibn Qurra, introduire des idées nouvelles importantes concernant factorisation et les méthodes combinatoires. Il a également donné la paire de nombres amiables 17 296, 18 416, qui ont été attribués à Euler, mais nous savons qu'ils ont été connus plus tôt que al-Farisi, peut-être même par Thabit ibn Qurra lui-même. Au 17ème siècle, Muhammad Baqir Yazdi a donné la paire de nombres amiables 9.363.584 et 9.437.056 encore de nombreuses années avant que la contribution d'Euler.

Early théorie des nombres européenne

La théorie des nombres a commencé en Europe, dans les 16e et 17e siècles, avec François Viète, Bachet de Meziriac, et surtout Fermat , dont méthode de descente infinie était la première preuve générale de questions diophantiennes. dernier théorème de Fermat a été posée comme un problème en 1637, une preuve de ce qui n'a pas été trouvé jusqu'en 1994. Fermat a également posé l'équation comme un problème en 1657.

Au XVIIIe siècle, Euler et Lagrange fait d'importantes contributions à la théorie des nombres. Euler a fait un travail sur théorie analytique des nombres, et trouvé une solution générale de l'équation . Lagrange a trouvé une solution à l'équation de Pell plus générale. Euler et Lagrange résolus ces équations Pell au moyen de fractions continues, si ce était plus difficile que l' indienne chakravala méthode.

Les débuts de la théorie des nombres moderne

Vers le début des livres du XIXe siècle de Legendre (1798), et Gauss mis ensemble les premières théories systématiques en Europe. Gauss Disquisitiones Arithmeticae (1801) peut être dit de commencer la théorie moderne des nombres.

La formulation de la théorie de congruences commence avec Disquisitiones de Gauss. Il a introduit le symbolisme

et exploré plus du domaine. Chebyshev publié en 1847 un ouvrage en russe sur le sujet, et en France Serret a popularisé.

Outre résumant les travaux antérieurs, Legendre a déclaré le loi de réciprocité quadratique. Cette loi, découvert par induction et énoncée par Euler, a d'abord été révélée par Legendre dans sa Théorie des Nombres (1798) pour les cas spéciaux. Indépendamment de Euler et Legendre, Gauss a découvert la loi à propos de 1795, et a été le premier à donner une preuve générale. L'ont également contribué à le sujet suivant: Cauchy; Dirichlet dont Vorlesungen über Zahlentheorie est un classique; Jacobi, qui a présenté le Symbole de Jacobi; Liouville, Zeller (?), Eisenstein, Kummer, et Kronecker. La théorie se étend pour inclure cubique et quartique réciprocité, (Gauss, Jacobi qui le premier se est avéré la loi de réciprocité cube, et Kummer).

Pour Gauss est également due la représentation des nombres par le binaire formes quadratiques.

Théorie des nombres premiers

Un thème récurrent et productif dans la théorie des nombres est l'étude de la répartition des nombres premiers. Carl Friedrich Gauss conjecturé la limite du nombre de nombres premiers ne dépassant pas un nombre donné (la théorème des nombres premiers) comme un adolescent.

Chebyshev (1850) a donné les limites utiles pour le nombre des nombres premiers entre deux limites données. Riemann introduit analyse complexe sur la théorie de la Fonction zêta de Riemann. Cela a conduit à une relation entre les zéros de la fonction zêta et de la distribution des nombres premiers, pour aboutir finalement à une preuve de théorème des nombres premiers indépendamment par Hadamard et de la Vallée Poussin en 1896. Toutefois, une preuve élémentaire a été donné plus tard par Paul Erdős et Atle Selberg en 1949. Voici des moyens élémentaires qu'il ne utilise pas de techniques d'analyse complexes; Toutefois, la preuve est encore très ingénieuse et difficile. Le Hypothèse de Riemann, ce qui donnerait des informations beaucoup plus précises, est encore une question ouverte.

Développements du XIXe siècle

Cauchy, Poinsot (1845), Lebesgue (1859, 1868), et notamment Hermite ont ajouté à ce sujet. Dans la théorie des formes ternaires, Eisenstein a été un leader, et à lui et à HJS Smith est aussi en raison d'une avancée notable dans la théorie des formes en général. Smith a donné une classification complète des formes quadratiques ternaires, et étendu les recherches de Gauss concernant réel formes quadratiques à formes complexes. Les enquêtes concernant la représentation des nombres par la somme de 4, 5, 6, 7, 8 places ont été avancés par Eisenstein et la théorie a été achevée par Smith.

Dirichlet a été la première à donner des conférences sur le sujet dans une université allemande. Parmi ses contributions est l'extension du dernier théorème de Fermat :

Euler et Legendre, qui avaient éprouvé pour (Et donc par voie de conséquence, tous les multiples de 3 et 4), montrant que Dirichlet . Parmi les écrivains français sont plus tard Borel; Poincaré, dont les mémoires sont nombreux et précieux; Tannery, et Stieltjes. Parmi les principaux contributeurs en Allemagne étaient Kronecker, Kummer, Schering, Bachmann, et Dedekind. En Autriche Vorlesungen über allgemeine la Arithmetik de Stolz (1885-1886), et en Angleterre La Théorie des Nombres de Mathews (Partie I, 1892) étaient des œuvres savantes générales. Genocchi, Sylvester, et JWL Glaisher ont également ajouté à la théorie.

Fin des développements du XIXe et du début du XXe siècle

Ce était l'époque des grands progrès dans la théorie des nombres grâce au travail des Axel Thue sur équations diophantiennes, de David Hilbert en théorie algébrique des nombres (il a également prouvé la De Waring nombre premier de conjecture), et à la création de la théorie des nombres géométrique par Hermann Minkowski, mais aussi grâce à Adolf Hurwitz, Georgy F. Voronoy, Waclaw Sierpinski, Derrick Lehmer Norman et plusieurs autres.

Développements du XXe siècle

Grandes figures en théorie des nombres XXe siècle comprennent Hermann Weyl, Nikolai Chebotaryov, Emil Artin, Erich Hecke, Helmut Hasse, Alexandre Gelfond, Yuri Linnik, Paul Erdős, Gerd Faltings, GH Hardy, Edmund Landau, Louis Mordell, John Edensor Littlewood, Srinivasa Ramanujan, André Weil, Ivan Vinogradov, Atle Selberg, Carl Siegel, Igor Shafarevich, John Tate, Robert Langlands, Goro Shimura, Kenkichi Iwasawa, Jean-Pierre Serre, Pierre Deligne, Enrico Bombieri, Alan Baker, Peter Swinnerton-Dyer, Bryan Birch, Vladimir Drinfeld, Laurent Lafforgue, Andrew Wiles, et Richard Taylor.

Jalons en théorie des nombres XXe siècle comprennent la preuve de théorème de Fermat par Andrew Wiles en 1994 et la preuve de la connexes Taniyama-Shimura conjecture en 1999.

Citations

• Les mathématiques sont la reine des sciences et la théorie des nombres est la reine des mathématiques -. Gauss
• Dieu a inventé les nombres entiers; tout le reste est l'œuvre de l'homme. - Kronecker