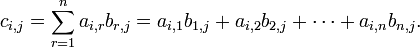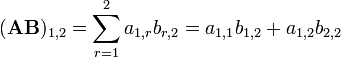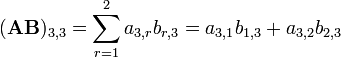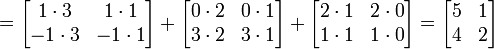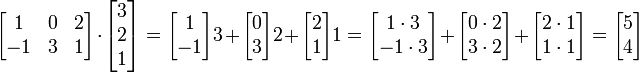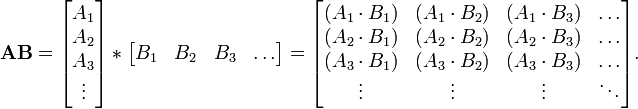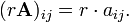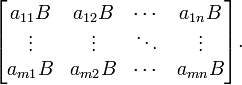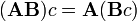La multiplication de matrices

Saviez-vous ...

SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

En mathématiques , la multiplication de matrices est l'opération consistant à multiplier un matrice soit avec un scalaire ou une autre matrice. Cet article donne un aperçu des différentes façons d'effectuer la multiplication de matrices.

Produit matriciel ordinaire

Ce est le moyen le plus souvent utilisé et le plus important de multiplier les matrices. Il est défini entre deux matrices que si le nombre de colonnes de la première matrice est le même que le nombre de rangées de la deuxième matrice. Si A est une matrice m -by- n et B est une matrice n -by- p, puis leur produit est une matrice de m -by- p désigné par AB (ou parfois A · B). Si C = AB et C _{i, j} désigne l'entrée en C à la position (i, j), puis

$c_ {i, j} = \ sum_ {r = 1} ^ n a_ {i, r} b_ {r, j} = a_ {i, 1} b_ {1, j} + a_ {i, 2} {b_ 2, j} + \ cdots + a_ {i, n} b_ {n, j}.$

pour chaque paire i et j avec 1 ≤ i ≤ M et 1 ≤ j ≤ p. Le système algébrique " unités de la matrice "résume les propriétés abstraites de ce genre de multiplication.

Calcul directement à partir de la définition

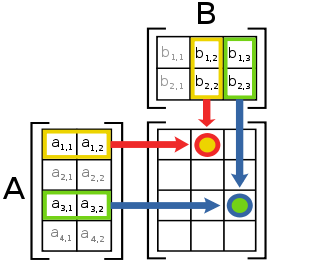
L'image de gauche montre comment calculer le (1,2) et l'élément (3,3) élément de AB si A est une matrice 4 × 2, et B est une matrice 2 × 3. Les éléments de chaque matrice sont appariés dans la direction des flèches; chaque paire est multiplié, et les produits sont ajoutés. L'emplacement du nombre résultant en AB correspond à la ligne et de la colonne qui ont été pris en considération.

$(\ Mathbf {AB}) _ {1,2} = \ sum_ {r = 1} ^ 2 a_ {1, r} B_ {r, 2} = {1,1} a_ b_ {1,2} + a_ {1,2} {2,2} b_$

$(\ Mathbf {AB}) _ {3,3} = \ sum_ {r = 1} ^ 2 a_ {3, r} B_ {R, 3} = {3,1} a_ b_ {1,3} + a_ {3,2} {2,3} b_$

Par exemple:

$\ Begin {} bmatrix 1 & 0 & 2 -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \ end {} bmatrix = \ begin {} bmatrix 1 \ 3 fois + 0 \ times 2 + 2 \ times 1 & 1 \ times 1 + 0 \ times 1 + 2 \ fois 0 -1 \\ \ fois 3 + 3 \ times 2 + 1 \ times 1 & -1 \ times 1 + 3 \ times 1 + 1 \ fois 0 \ end {} bmatrix = \ begin {} bmatrix 5 & 1 \\ 4 & 2 \ end {} bmatrix$

Procédé coefficients vecteurs

Cette multiplication de matrice peut également être considérée du point de vue légèrement différent: il ajoute des vecteurs ainsi après avoir été multiplié par différents coefficients. Si A et B sont des matrices donnés par:

$\ Mathbf {A} = \ begin {} bmatrix a_ {1,1} & a_ {1,2} \ & points \\ a_ {2,1} et {2,2} a_ \ & points \\ \ & vdots \ & vdots \ ddots \ end {} bmatrix$ et $\ Mathbf {B} = \ begin {} bmatrix b_ {1,1} & b_ {1,2} \ & points \\ b_ {2,1} et {2,2} b_ & \ dots \\ \ & vdots \ & vdots \ ddots \ end {} bmatrix = \ begin {} bmatrix B_1 \\ B_2 \\ \ vdots \ end {} bmatrix$

puis

$\ Mathbf {AB} = \ begin {} bmatrix a_ {1,1} B_1 + a_ {1,2} B_2 + \ cdots de la a_ {2,1} B_1 + a_ {2,2} B_2 + \ cdots \\ \ vdots \ end {} bmatrix$

L'exemple revisité:

$\ Begin {} bmatrix 1 & 0 & 2 -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \ end {} bmatrix = \ begin {} bmatrix 1 \ begin {} bmatrix 3 & 1 \ end {} bmatrix + 0 \ begin {} bmatrix 2 & 1 \ end {} bmatrix + 2 \ begin {} bmatrix 1 & 0 \ end {} \\ bmatrix -1 \ begin {} bmatrix 3 & 1 \ end {} bmatrix + 3 \ begin {} bmatrix 2 & 1 \ end {} bmatrix + 1 \ begin {} bmatrix 1 & 0 \ end {bmatrix} \ end {} bmatrix = \ begin {bmatrix} \ begin {} bmatrix 3 & 1 \ end {} bmatrix + \ begin {} bmatrix 0 & 0 \ end {} bmatrix + \ begin {} bmatrix 2 & 0 \ end {} bmatrix \\ \ begin {} bmatrix -3 et -1 \ end {} bmatrix + \ begin {} bmatrix 6 et 3 \ end {} bmatrix + \ begin {} bmatrix 1 & 0 \ end {bmatrix} \ end {} bmatrix$

$= \ Begin {} bmatrix 5 & 1 \\ 4 & 2 \ end {} bmatrix$

Les lignes de la matrice sont à gauche de la liste des coefficients. La matrice sur la droite est la liste des vecteurs. Dans l'exemple, la première ligne est [1 0 2], et donc nous prenons une fois le premier vecteur, 0 fois le second vecteur, et deux fois la troisième vecteur.

L'équation peut être simplifiée en utilisant en outre produits extérieurs:

$\ Mathbf {A} = \ begin {} bmatrix A_1 & A_2 & \ dots \ end {bmatrix} \ implique \ mathbf {AB} = \ sum_i A_iB_i$

Les termes de cette somme sont des matrices de la même forme, chacune décrivant l'effet d'une colonne de A et une rangée de B sur le résultat. Les colonnes de A peuvent être considérés comme un système de coordonnées de la transformation, ce est à dire étant donné un vecteur x nous avons 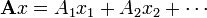$\ mathbf {a} x = A_1x_1 + A_2x_2 + \ cdots$ où $x_i$ sont des coordonnées le long de la 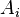$A_i$ "Axes". Les termes 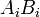$A_iB_i$ sont comme 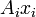$A_ix_i$ , Excepté 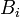$B_i$ contient la i ième coordonnée pour chaque vecteur de colonne de B, dont chacun est indépendamment transformé en parallèle.

L'exemple revisité:

$\ Begin {} bmatrix 1 & 0 & 2 -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \ end {} bmatrix = \ begin {} bmatrix 1 \\ -1 \ end {bmatrix} \ begin {} bmatrix 3 & 1 \ end {} bmatrix + \ begin {} 0 bmatrix \\ 3 \ end {bmatrix} \ begin {} bmatrix 2 & 1 \ end {} bmatrix + \ begin {} bmatrix 2 \\ 1 \ end {bmatrix} \ begin {} bmatrix 1 & 0 \ end {} bmatrix$

$= \ Begin {} bmatrix 1 \ cdot 3 & 1 \ cdot 1 \\ -1 \ cdot 3 et -1 \ cdot 1 \ end {} bmatrix + \ begin {} 0 bmatrix \ cdot 2 & 0 \ cdot 1 \\ 3 \ cdot 2 & 3 \ cdot 1 \ end {} bmatrix + \ begin {} bmatrix 2 \ cdot 1 & 2 \ cdot 0 1 \\ \ cdot 1 & 1 \ cdot 0 \ end {} bmatrix = \ begin {bmatrix } 5 & 1 \\ 4 & 2 \ end {} bmatrix$

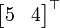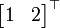Les vecteurs $\ Begin {} bmatrix 3 & 2 & 1 \ end {bmatrix} ^ \ top$ et $\ Begin {} bmatrix 1 & 1 & 0 \ end {bmatrix} ^ \ top$ ont été transformés à $\ Begin {} bmatrix 5 & 4 \ end {bmatrix} ^ \ top$ et $\ Begin {} bmatrix 1 & 2 \ end {bmatrix} ^ \ top$ en parallèle. On pourrait aussi les transformer un par un avec les mêmes étapes:

$\ Begin {} bmatrix 1 & 0 & 2 -1 \\ & 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 \\ \\ 2 1 \ end {} bmatrix = \ begin {} bmatrix 1 \ \ -1 \ end {} bmatrix 3+ \ begin {} 0 bmatrix \\ 3 \ end {} bmatrix 2+ \ begin {} bmatrix 2 \\ 1 \ end {} bmatrix 1 = \ begin {} bmatrix 1 \ cdot 3 -1 \\ \ cdot 3 \ end {} bmatrix + \ begin {} 0 bmatrix \ cdot 2 \\ 3 \ cdot 2 \ end {} bmatrix + \ begin {} bmatrix 2 \ cdot 1 \\ 1 \ cdot 1 \ end {} bmatrix = \ begin {} bmatrix 5 4 \\ \ end {} bmatrix$

Méthode vectorielle listes

Le produit de la matrice ordinaire peut être considéré comme un dot produit d'une colonne liste des vecteurs et un rangée liste des vecteurs. Si A et B sont des matrices donnés par:

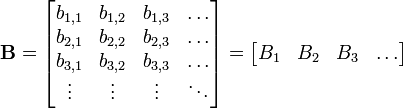
$\ Mathbf {A} = \ begin {} bmatrix a_ {1,1} et {1,2} a_ & a_ {1,3} \ & points \\ a_ {2,1} et {2,2} a_ & a_ {2,3} \ & points \\ a_ {3,1} et {3,2} a_ & a_ {3,3} \ & points \\ \ vdots & \ vdots & \ & vdots \ ddots \ end { bmatrix} = \ begin {} bmatrix A_1 \\ \\ A_2 A_3 \\ \ vdots \ end {} bmatrix$ et $\ Mathbf {B} = \ begin {} bmatrix b_ {1,1} & b_ {1,2} & b_ {1,3} \ & points \\ b_ {2,1} et {2,2} b_ & b_ {2,3} \ & points \\ b_ {3,1} et {3,2} b_ & b_ {3,3} et \ dots \\ \ vdots & \ vdots & \ & vdots \ ddots \ end { bmatrix} = \ begin {} bmatrix B_1 & B_2 & B_3 & \ dots \ end {} bmatrix$

où

A ₁ est le vecteur ligne de tous les éléments de la forme a _{une, x} A ₂ est le vecteur ligne de tous les éléments de la forme a _{2, x} etc,

et B ₁ est le vecteur colonne de tous les éléments de la forme b _{x, 1} B ₂ est le vecteur colonne de tous les éléments de la forme b _{x, 2} etc,

puis

$\ Mathbf {AB} = \ begin {} bmatrix A_1 \\ \\ A_2 A_3 \\ \ vdots \ end {} bmatrix * \ begin {} bmatrix B_1 & B_2 & B_3 & \ dots \ end {} bmatrix = \ begin { bmatrix} (A_1 \ cdot b_1) et (A_1 \ cdot B_2) et (A_1 \ cdot B_3) & \ dots \\ (A_2 \ cdot B_1) & (A_2 \ cdot B_2) & (A_2 \ cdot B_3) & \ dots \\ (A_3 \ cdot B_1) & (A_3 \ cdot B_2) & (A_3 \ cdot B_3) & \ dots \\ \ vdots & \ vdots & \ & vdots \ ddots \ end {} bmatrix.$

Propriétés

La multiplication de matrices ne est pas commutative (ce est-à AB de la BA), sauf dans des cas particuliers. Il est facile de voir pourquoi: vous ne pouvez pas vous attendre à passer les proportions avec les vecteurs et obtenir le même résultat. Il est également facile de voir comment l'ordre des facteurs qui détermine le résultat, quand on sait que le nombre de colonnes dans la matrice des proportions doit être le même que le nombre de lignes de la matrice des vecteurs: ils doivent représenter le même nombre de vecteurs.

Bien que la multiplication de matrices ne est pas commutative, les déterminants de AB et BA sont toujours égaux (si A et B sont des matrices carrées de même taille). Voir l'article sur les déterminants pour une explication. Cependant la multiplication de matrices est commutative lorsque les deux matrices sont diagonale et de la même dimension.

Cette notion de multiplication est important parce que si A et B sont interprétées comme transformations linéaires (qui est presque universellement fait), puis le produit matriciel AB correspond à la composition des deux transformations linéaires, avec B étant appliqués en premier.

En outre, toutes les notions de la multiplication de matrices décrites ici part un ensemble de propriétés communes décrites ci-dessous.

Algorithmes

Le complexité de la multiplication de matrices, si elle est effectuée naïvement, est O (n ³), mais des algorithmes plus efficaces existent. L'algorithme de Strassen, conçu par Volker Strassen en 1969 et souvent appelée «la multiplication de matrices rapide", est basé sur une façon intelligente de multiplier deux matrices 2 × 2 qui exige seulement 7 multiplications (au lieu de l'habituel 8). Appliquant cette astuce donne de manière récursive un algorithme avec un coût de 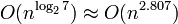$O (n ^ {\ log_ {2}} 7) \ environ O (n ^ {2,807})$ . En pratique, cependant, il est rarement utilisé car il est difficile à mettre en œuvre et il manque stabilité numérique. Le facteur constant implicite dans le Comparaison asymptotique est d'environ 4,695.

Le algorithme avec l'exposant le plus bas connu, qui a été présenté par Don Coppersmith et Shmuel Winograd en 1990 , a une complexité asymptotique de O (n ^2,376). Il est similaire à l'algorithme de Strassen: une façon intelligente est conçu pour multiplier deux matrices k × k avec moins de multiplications ³ k, et cette technique est appliquée de manière récursive. Il améliore le facteur constant dans l'algorithme de Strassen, réduisant à 4,537. Cependant, le terme constant impliqué dans le O (n ^2,376) résultat est si grande que l'algorithme Coppersmith-Winograd ne vaut que pour les matrices qui sont trop gros pour gérer sur les ordinateurs actuels (Knuth, 1998).

Depuis ne importe quel algorithme pour multiplier deux matrices n × n doit traiter tous les 2 × n ² entrées, il ya une borne inférieure asymptotique des opérations Ω (n) ². Raz (2002) prouve une borne inférieure de 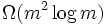$\ Omega (m ^ 2 \ log m)$ pour coefficient bornées circuits arithmétiques sur les nombres réels ou complexes.

Cohn et al. (2003, 2005) mis des méthodes telles que les algorithmes Strassen et Coppersmith-Winograd dans un tout autre, théorie des groupes contexte. Ils montrent que si les familles de produits de couronnes de abélien avec des groupes symétriques satisfaisant certaines conditions existent, algorithmes matrice de multiplication avec une complexité quadratique essentielle existent. La plupart des chercheurs croient que ce est effectivement le cas (Robinson, 2005).

Multiplication scalaire

La multiplication scalaire d'une matrice A = (a _ij) et un scalaire r r donne un produit A de la même taille que A. Les entrées de r A sont donnés par

$(R \ mathbf {A}) _ {} ij = r \ cdot a_ {ij}. \,$

Par exemple, si

$\ Mathbf {A} = \ begin {} bmatrix 1 & 2 \\ 3 & 4 \ end {} bmatrix$

puis

$7 \ mathbf {A} = \ begin {} bmatrix 7 \ cdot 1 et 7 \ cdot 2 \\ 7 \ cdot 3 & 7 \ cdot 4 \ end {} bmatrix = \ begin {} bmatrix 7 & 14 21 \\ & 28 \ end {} bmatrix.$

Si nous sommes préoccupés par les matrices sur une anneau, puis la multiplication ci-dessus est parfois appelé la multiplication gauche tandis que la droite multiplication est définie comme

$(\ Mathbf {A} r) _ {ij} = {a_ ij} \ cdot r. \,$

Lorsque l'anneau sous-jacent est commutatif , par exemple, le champ de nombre réel ou complexe, les deux multiplications sont les mêmes. Toutefois, si l'anneau ne est pas commutative, telle que la quaternions, ils peuvent être différents. Par exemple

$i \ begin {} i bmatrix & 0 0 \\ & j \\ \ end {} bmatrix = \ begin {} bmatrix -1 et 0 0 \\ & k \\ \ end {} bmatrix \ ne \ begin {} bmatrix -1 et 0 0 \\ & -k \\ \ end {} bmatrix = \ begin {} i bmatrix & 0 0 \\ & j \\ \ end {} i bmatrix.$

Produit Hadamard

Pour les deux matrices de mêmes dimensions, on a le produit de Hadamard, également connu sous le nom de produit et le produit entrywise Schur. Il peut être généralisée à tenir non seulement pour les matrices mais aussi pour les opérateurs. Le Hadamard produit de deux m -by- n matrices A et B, notée A • B est une matrice n m -by- donnée par (A • B) a _{ij ij} = b _ij. Par exemple

$\ Begin {} bmatrix 1 & 2 & 3 1 \\ \\ \ end {} bmatrix \ bullet \ begin {} bmatrix 0 et 3 \\ 2 & 1 \\ \ end {} bmatrix = \ begin {} bmatrix 1 \ cdot 0 et 2 \ cdot 3 \\ 3 \ cdot 2 & 1 \ cdot 1 \\ \ end {} bmatrix = \ begin {} bmatrix 0 et 6 \\ 6 & 1 \\ \ end {} bmatrix$ .

Notez que le produit est un Hadamard sous-matrice du produit de Kronecker (voir ci-dessous).

Le produit Hadamard est commutative .

Le produit Hadamard est étudié par les théoriciens de la matrice, et il apparaît dans algorithmes de compression avec perte tels que JPEG, mais il est pratiquement épargnée par algébristes linéaires. Il est discuté dans (Horn & Johnson, 1994, Ch. 5).

Produit de Kronecker

Pour tout deux matrices arbitraires A et B, nous avons le produit direct ou Produit de Kronecker A ⊗ B défini comme

$\ Begin {} bmatrix a_ {11} B & a_ {12} B & \ & cdots a_ {} B 1n \\ \ vdots & \ vdots & \ & ddots \ vdots \\ a_ {m1} B & a_ {} m2 B & \ & cdots a_ {mn} B \ end {} bmatrix.$

Notez que si A est m -by- n et B est de p r alors A ⊗ B est un mp -by- nr matrice. Encore une fois cette multiplication ne est pas commutative.

Par exemple

$\ Begin {} bmatrix 1 & 2 & 3 1 \\ \\ \ end {bmatrix} \ otimes \ begin {} bmatrix 0 et 3 \\ 2 & 1 \\ \ end {} bmatrix = \ begin {} bmatrix 1 \ cdot 0 & 1 \ cdot 3 & 2 \ cdot 0 et 2 \ cdot 3 \\ 1 \ cdot 2 & 1 \ cdot 1 & 2 \ cdot 2 & 2 \ cdot 1 \\ 3 \ cdot 0 et 3 \ cdot 3 & 1 \ cdot 0 & 1 \ cdot 3 \\ 3 \ cdot 2 & 3 \ cdot 1 & 1 \ cdot 2 & 1 \ cdot 1 \\ \ end {} bmatrix = \ begin {} bmatrix 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 et 9 et 0 et 3 \\ 6 & 3 & 2 & 1 \ end {} bmatrix$ .

Si A et B représentent des transformations linéaires V ₁ → W ₁ et W ₂ → V _2, respectivement, alors A ⊗ B représente le produit tenseur des deux cartes, _une V ⊗ V ₂ → W ₁ ⊗ W _2.

Propriétés communes

Le Wikibook Le Livre de preuves mathématiques a une page sur le thème de: Les preuves de propriétés des matrices

Tous les trois notions de multiplication de matrices sont associative :

$\ \ Mathbf {A} (\ mathbf {BC}) = (\ mathbf {AB}) \ mathbf {C}$

et distributive:

$\ \ Mathbf {A} (\ mathbf {B} + \ mathbf {C}) = \ mathbf {AB} + \ mathbf {AC}$

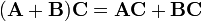$\ (\ Mathbf {A} + \ mathbf {B}) \ mathbf {C} = \ mathbf {AC} + \ mathbf {BC}$ .

et compatible avec multiplication scalaire:

$\ C (\ mathbf {AB}) = (c \ mathbf {A}) \ mathbf {B}$

$\ (\ Mathbf {A} c) \ mathbf {B} = \ mathbf {A} (c \ mathbf {B})$

$\ (\ Mathbf {AB}) c = \ mathbf {A} (\ mathbf {B} c)$

Notez que ces trois couples séparés d'expressions seront égaux entre eux que si la multiplication et l'addition sur le champ scalaire sont commutative, ce est à dire le champ scalaire est un anneau commutatif. Voir multiplication scalaire ci-dessus pour un contre-exemple comme le champ scalaire de quaternions.

Produit interne Frobenius

Le produit intérieur Frobenius, parfois notée A: B est le produit intérieur composante par composante de deux matrices comme se ils sont des vecteurs. En d'autres termes, ce est la somme des entrées du produit, ce est-Hadamard,

$\ Mathbf {A}: \ mathbf {B} = \ sum_i \ sum_j A_ {ij} {B_ ij} = \ operatorname {trace} (\ mathbf {A} ^ T \ mathbf {B}) = \ operatorname {trace} (\ mathbf {A} \ mathbf {B} ^ T).$

Ce produit intérieure induit la Norme de Frobenius.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Matrix_multiplication&oldid=203157436 "

Privacy Policy and Contacts (IT)

La multiplication de matrices

Saviez-vous ...

Produit matriciel ordinaire

Calcul directement à partir de la définition

Procédé coefficients vecteurs

Méthode vectorielle listes

Propriétés

Algorithmes

Multiplication scalaire

Produit Hadamard

Produit de Kronecker

Propriétés communes

Produit interne Frobenius