La théorie des groupes

En algèbre abstraite , la théorie des groupes étudie les structures algébriques connus sous le nom des groupes . A est un groupe Set G (le jeu sous-jacent) fermé sous un binaire fonctionnement satisfaisant de trois axiomes:

1. L'opération est associative .
2. L'opération a un élément d'identité.
3. Chaque élément a une élément inverse.

(Lire la suite pour des définitions plus précises.)

Les groupes sont des blocs de construction plus élaborées structures algébriques tels que bagues, les champs et les espaces vectoriels , et se reproduisent tout au long de mathématiques. La théorie des groupes a de nombreuses applications dans la physique et la chimie , et est potentiellement applicable dans toute situation caractérisée par la symétrie .

L'ordre d'un groupe est la cardinal de G; groupes peuvent être de fini ou ordre infini. Le classification des groupes simples finis est une réalisation majeure mathématique du 20e siècle.

concepts de la théorie de groupe

Pour les non-mathématiciens

Un groupe est constitué d'une collection de objets abstraits ou des symboles, et une règle pour les combiner. La règle de combinaison indique comment ces objets doivent être manipulés. Ainsi les groupes sont un moyen de faire des mathématiques avec des symboles à la place de chiffres concrets.

Plus précisément, on peut parler d'un groupe à chaque fois qu'un définir, avec un opération qui combine toujours deux éléments de cet ensemble, par exemple, un x b, remplit toujours les exigences suivantes:

1. La combinaison des deux éléments de l'ensemble donne un élément du même ensemble ( fermeture);
2. Le bracketing est sans importance ( associativité ): a × (b × c) = (a × b) x c;
3. Il ya un élément qui ne provoque pas qu'il arrive quelque chose ( élément d'identité): a × 1 = 1 × a = a;
4. Chaque élément a a une "image miroir" ( élément inverse) 1 / une qui a la propriété pour obtenir l'élément d'identité lorsqu'il est combiné avec un: a × 1 / a = 1 / a × a = 1

Cas particulier: Si l'ordre des opérandes ne affecte pas le résultat, ce est si une × b = b × a détient ( commutativité ), nous parlons d'un groupe abélien.

Quelques exemples numériques simples de groupes abéliens sont:

• Entiers avec l'opération d'addition "+" comme opération binaire zéro et comme élément d'identité
• Nombres rationnels sans nul avec la multiplication «x» comme opération binaire et le numéro un en tant qu'élément d'identité. Zéro doit être exclue parce qu'elle ne dispose pas d'un élément inverse. ("1/0" ne est pas défini.)

Cette définition des groupes est volontairement très générale. Il permet de traiter que des groupes non seulement des ensembles de nombres avec des opérations correspondantes, mais aussi d'autres objets abstraits et des symboles qui remplissent les propriétés requises, telles que des polygones avec leurs rotations et de réflexions dans groupes dièdre.

James Newman résumé la théorie des groupes comme suit:

Définition d'un groupe

Un groupe (G, *) est un Set G fermée en vertu d'un * opération binaire satisfaisant à la suite 3 axiomes:

• Associativité : Pour tout a, b et c dans G, (a * b) * c = a * (b * c).
• élément de l'identité: Il existe e ∈ G tel que pour tout a dans G, e * a = a * e = a.
• Élément Inverse: Pour chaque un à G, il existe un élément b de G tel que b = a * b * a = e, où e est l'élément d'identité.

Dans la terminologie de algèbre universelle, un groupe est un variété, et un 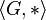algèbre de type .

Sous-groupes

Un ensemble H est un sous-groupe d'un groupe G si ce est un sous-ensemble de G et est un groupe en utilisant l'opération définie sur G. En d'autres termes, H est un sous-groupe de (G, *) si la restriction de * H est une opération de groupe sur H.

Un sous-groupe H est un sous-groupe normal de G si pour tout h dans H et G dans G, ^-1 GES est également en H. Une alternative (mais équivalent) définition est qu'un sous-groupe est normal si sa gauche et à droite cosets coïncident. Les sous-groupes normaux jouent un rôle distingué en vertu du fait que la collection de classes à un sous-groupe de N normale dans un groupe G hérite naturellement une structure de groupe, ce qui permet la formation de la groupe quotient, généralement notée G / N (parfois aussi appelé un groupe de facteur).

Opérations impliquant des groupes

Un homomorphism est une carte entre deux groupes qui préserve la structure imposée par l'opérateur. Si la carte est bijective, alors ce est un isomorphisme. Un isomorphisme d'un groupe à lui-même est un automorphisme. L'ensemble des automorphismes d'un groupe est un groupe appelé le groupe d'automorphismes. Le un noyau de homomorphisme est un sous-groupe du groupe.

Un action de groupe est une carte impliquant un groupe et un ensemble, où chaque élément dans le groupe définit une bijection sur un ensemble. actions de groupe sont utilisés pour prouver la Sylow théorèmes et de prouver que le centre d'un p-groupe ne est pas triviale.

Types particuliers de groupes

Un groupe est:

• Abelian (ou commutative ) si ses déplacements de produits (ce est, pour tout a, b dans G, a * b = b * a). Un groupe non commutatif est un groupe qui ne est pas abélien. Le terme "abélien" honore le mathématicien Niels Abel.

• Cyclique si elle est généré par un seul élément.

• Simple si elle n'a pas de sous-groupes normaux non triviaux.

• Soluble (soluble ou) si elle a une série normale dont groupes quotients sont tous abélien. Le fait que S _5, le groupe symétrique en cinq éléments, ne est pas résoluble est utilisé pour prouver que certains polynômes quintiques ne peuvent être résolus par les radicaux.

• Libre se il existe un sous-ensemble de G, H, de telle sorte que tous les éléments de G peuvent être écrites uniquement comme produits (ou chaînes) d'éléments de H. Chaque groupe est le homomorphe l'image de certains groupe libre.

Certains théorèmes utiles

Certains résultats de base à la théorie des groupes élémentaire :

• Le théorème de Lagrange: si G est un groupe fini et H est un sous-groupe de G, alors l'ordre (ce est, le nombre d'éléments) de H divise l'ordre de G.
• De Cayley Théorème: chaque groupe G est isomorphe à un sous-groupe de la groupe symétrique sur G.
• Sylow théorèmes: si p ⁿ (et premier p) est la plus grande puissance de p divisant l'ordre d'un groupe fini G, alors il existe un sous-groupe d'ordre p ^n. Ce est peut-être le résultat de base la plus utile sur les groupes finis.
• Le Papillon lemme est un résultat technique sur le réseau de sous-groupes d'un groupe.
• Le Théorème fondamental sur homomorphismes concerne la structure de deux objets entre lesquels un homomorphisme est donnée, et le noyau et l'image de l'homomorphisme.
• Jordan-Hölder théorème: une série deux de composition d'un groupe donné sont équivalentes.
• Krull-Schmidt théorème: un groupe G satisfaisant certaines conditions de finitude pour les chaînes de ses sous-groupes, peut être écrit de manière unique comme un produit direct fini de sous-groupes indécomposables.
• De Burnside lemme: le nombre d'orbites d'un action de groupe sur un ensemble est égal au nombre moyen de points fixes par chaque élément du groupe.

Connexion de groupes et de symétrie

Étant donné un objet structuré d'aucune sorte, une symétrie est une cartographie de l'objet sur lui-même qui préserve la structure. Par exemple, les rotations d'une sphère sont symétries de la sphère. Si l'objet est un ensemble sans structure supplémentaire, une symétrie est un bijection de l'ensemble lui-même. Si l'objet est un ensemble de points dans le plan de son Structure métrique, une symétrie est une bijection de l'ensemble à lui-même qui préserve les distances entre chaque paire de points (e isométrie).

Les axiomes d'un groupe de formaliser les aspects essentiels de la symétrie .

1. Clôture de la loi de groupe - Cette dit que si vous prenez une symétrie d'un objet, puis appliquez une autre symétrie, le résultat sera toujours une symétrie.
2. L'existence d'une identité - Ceci indique que le maintien de l'objet fixe est toujours une symétrie d'un objet.
3. L'existence des inverses - Ce dit que chaque symétrie peut être annulée.
4. Associativité - Depuis symétries sont des fonctions sur un espace, et la composition de fonctions sont associative, cet axiome est nécessaire pour faire un groupe formel se comportent comme des fonctions.

Le théorème de Frucht dit que chaque groupe est le groupe de symétrie de certaines graphique. Ainsi, chaque groupe abstraite est en fait les symétries d'un objet explicite.

Applications de la théorie de groupe

Certaines applications importantes de la théorie de groupe comprennent:

• Les groupes sont souvent utilisées pour capturer la symétrie interne d'autres structures. Une symétrie de la structure interne est généralement associée à une invariant; l'ensemble de transformations qui conservent cette propriété invariante, conjointement avec l'opération de composition de transformations, forment un groupe appelé groupe de symétrie. Voir aussi groupe d'automorphismes.

• Galois théorie , qui est l'origine historique de la notion de groupe, utilise des groupes pour décrire les symétries des racines d'un polynôme (ou plus précisément les automorphismes des algèbres générés par ces racines). Les groupes solubles sont ainsi nommé en raison de leur rôle de premier plan dans cette théorie. La théorie de Galois a été initialement utilisée pour prouver que les polynômes de la cinquième degré et plus ne peuvent pas, en général, être résolus sous forme fermée par les radicaux, la façon dont les polynômes de degré inférieur peuvent.

• Groupes abéliens, qui ajoutent de la propriété commutative a * b = b * a, à la base de plusieurs autres structures dans l'algèbre abstraite, tels que des bagues, des champs et des modules.

• En topologie algébrique, les groupes sont utilisés pour décrire des invariants espaces topologiques. Ils sont appelés "invariants", car ils sont définis de telle manière qu'ils ne changent pas si l'espace est soumis à une certaine déformation. Les exemples incluent le groupe fondamental, groupes d'homologie et groupes de cohomologie. Le nom du sous-groupe de torsion d'un groupe infini montre l'héritage de la topologie en théorie des groupes.

• Le concept de la groupe de Lie (du nom du mathématicien Sophus Lie) est important dans l'étude des équations différentielles et collecteurs ; ils décrivent les symétries de structures géométriques et analytiques continues. Analyse sur ces et d'autres groupes est appelé analyse harmonique.

• Dans la combinatoire , la notion de permutation groupe et la notion d'action de groupe sont souvent utilisés pour simplifier le comptage d'un ensemble d'objets; voir en particulier Lemme de Burnside.

• Une bonne compréhension de la théorie des groupes est également important en physique et en chimie et science des matériaux. En physique, les groupes sont importants car ils décrivent les symétries laquelle les lois de la physique semblent obéir. Les physiciens sont très intéressés par les représentations du groupe, en particulier des groupes de Lie, car ces représentations font souvent la voie aux théories physiques "possibles". Des exemples de l'utilisation de groupes en physique comprennent: modèle standard , théorie de jauge, Groupe de Lorentz, Groupe de Poincaré

• Dans la chimie , les groupes sont utilisés pour classer les structures cristallines, polyèdres réguliers, et de la symétries de molécules. Les groupes de points attribués peuvent ensuite être utilisées pour déterminer les propriétés physiques (telles que polarité et chiralité), propriétés spectroscopiques (particulièrement utile pour Spectroscopie Raman et La spectroscopie infrarouge), et de construire des orbitales moléculaires.

• La théorie des groupes est largement utilisé dans cryptographie à clé publique. En Elliptic Curve Cryptography-, très grands groupes d'ordre premier sont construits en définissant les courbes elliptiques sur les corps finis.

Histoire

Il ya trois racines historiques de la théorie des groupes: la théorie de équations algébriques, la théorie des nombres et de la géométrie . Euler , Gauss , Lagrange , Abel et mathématicien français Galois étaient premiers chercheurs dans le domaine de la théorie des groupes. Galois est honoré comme la théorie de premier groupe de liaison et mathématicien théorie des champs, avec la théorie qui est maintenant appelé la théorie de Galois .

Une source tôt se produit dans le problème de la formation d'une équation e degré ayant que ses racines m des racines d'un données 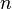équation e degré ( 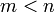). Pour les cas simples le problème remonte à Hudde (1659). Saunderson (1740) a indiqué que la détermination des facteurs d'une expression quadratique biquadratique conduit nécessairement à une équation du sixième degré, et Le Sœur (1748) et Waring (1762-1782) encore élaboré l'idée.

Une base commune pour la théorie des équations sur la base du groupe de permutations a été trouvé par le mathématicien Lagrange (1770, 1771), et cela a été construit la théorie de substitutions. Il a découvert que les racines de toutes les résolvantes (résolvantes, réduites) qu'il examina sont des fonctions rationnelles des racines des équations respectives. Pour étudier les propriétés de ces fonctions, il a inventé un Calcul des Combinaisons. Le travail contemporain de Vandermonde (1770) préfigure également la théorie à venir.

Ruffini (1799) a tenté une preuve de l'impossibilité de résoudre le quintique et équations plus élevés. Ruffini distingue ce qu'on appelle aujourd'hui et intransitif transitive, et imprimitive et groupes primitifs, et (1801) utilise le groupe d'une équation sous le nom de l'assieme delle permutazioni. Il a également publié une lettre de Abbati à lui-même, dans laquelle l'idée de groupe est importante.

Galois constaté que si 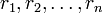sont les 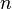racines d'une équation, il ya toujours un groupe de permutations de la 'S tel que (1) toutes les fonctions des racines invariables par les substitutions du groupe est rationnellement connu, et (2), à l'inverse, chaque fonction rationnelle déterminable des racines est invariant sous les substitutions du groupe. Galois a également contribué à la théorie de équations modulaires et à celle de fonctions elliptiques. Sa première publication sur la théorie des groupes a été faite à l'âge de dix-huit ans (1829), mais ses contributions attiré peu d'attention jusqu'à la publication de ses papiers collectés en 1846 (Liouville, vol. XI).

Arthur Cayley et Augustin Louis Cauchy ont été parmi les premiers à apprécier l'importance de la théorie, et à celui-ci en particulier sont dus un certain nombre de théorèmes importants. Le sujet a été popularisé par Serret, qui a consacré la section IV de son algèbre à la théorie; par Camille Jordan, dont le Traité des substitutions est un classique; et à Eugen Netto (1882), dont la théorie de substitutions et de ses applications à l'algèbre a été traduit en anglais par Cole (1892). D'autres théoriciens du groupe du XIXe siècle étaient Bertrand, Charles Hermite, Frobenius, Leopold Kronecker, et Emile Mathieu.

Walther von Dyck a été le premier (en 1882) pour définir un groupe dans le sens abstrait complète de cette entrée.

L'étude de ce qu'on appelle aujourd'hui Groupes de Lie, et de leur les sous-groupes distincts, que groupes de transformation, ont commencé en 1884 avec systématiquement Sophus Lie; suivi par le travail des Tuer, Étude, Schur, Maurer, et Cartan. Le discontinue ( groupe discret) de la théorie a été construit par Felix Klein, Lie, Poincaré, et Charles Émile Picard, dans le cadre en particulier formes modulaires et monodromie.

Le classification des groupes simples finis est un vaste ensemble de travaux à partir du milieu du 20ème siècle, classer tous les fini groupes simples.

Autres contributeurs importants à la théorie de groupe comprennent Emil Artin, Emmy Noether , Sylow, et bien d'autres.

Alfred Tarski prouvé la théorie de groupe élémentaire indécidable.

Recueil

Une application de la théorie des groupes est la théorie des ensembles de musique.

Dans la philosophie , Ernst Cassirer théorie des groupes liés à la théorie de la perception de Gestalt psychologie. Il a pris la Constance perceptive de cette psychologie comme analogue à la invariants de la théorie des groupes.