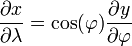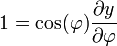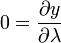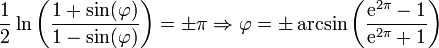Projection de Mercator
Contexte des écoles Wikipédia
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . enfants SOS est le plus grand don de charité du monde enfants orphelins et abandonnés la chance de la vie familiale.

La projection de Mercator est une projection cartographique cylindrique présenté par le Géographe et cartographe flamand Gerardus Mercator, en 1569. Il est devenu la projection cartographique standard à des fins nautiques en raison de sa capacité à représenter des lignes de constante relèvement vrai ou vrai bien sûr, connu sous le nom loxodromies, que droite des segments de ligne. Bien que la direction et les formes sont exacts sur une projection de Mercator, il déforme la taille, à un degré de plus en plus loin de l'équateur.
Propriétés et détails historiques
1569 édition de Mercator était un grand Planisphère mesure 202 par 124 cm, imprimées en dix-huit feuilles séparées. Comme dans toutes les projections cylindriques , parallèles et méridiens sont rectilignes et perpendiculaires entre elles. Dans l'accomplissement de cela, est-ouest inévitable étirement de la carte, ce qui augmente comme distance des équateur augmente, est accompagné d'un nord-sud correspondant étirement, de sorte que, à chaque emplacement du point, l'échelle est-ouest est le même que l'échelle nord-sud, ce qui rend la projection conformationnelle. Une carte Mercator ne peut jamais montrer pleinement les régions polaires, depuis échelle linéaire devient infiniment élevée au niveau des pôles. Être une projection conforme, les angles sont conservés dans tous les endroits, cependant échelle varie d'un endroit à l'autre, faussant la taille des objets géographiques. En particulier, les zones proches des pôles sont plus touchés, de transmettre une image de la géométrie de la planète qui est plus faussé les plus près des pôles. À des latitudes supérieures à 70 ° nord ou au sud, la projection de Mercator est pratiquement inutilisable.

Toutes les lignes de constante palier ( loxodromies ou loxodromes - ceux qui font des angles constants avec les méridiens), sont représentés par des segments de droite sur une carte Mercator. Ce est précisément le type d'itinéraire habituellement utilisés par les navires en mer, où compas sont utilisés pour indiquer les directions géographiques et de diriger les navires. Les deux propriétés, conformalité et droit lignes de rhumb, faire cette projection unique adapté à la navigation maritime: cours et les roulements sont mesurées à l'aide vent roses ou rapporteurs, et les directions correspondantes sont facilement transférées de point à point, sur la carte, à l'aide d'un règle parallèle ou une paire de carrés de navigation.
Le nom et des explications données par Mercator à sa carte du monde (Nova et Aucta Orbis Terrae Descriptio annonce Usum Navigatium Emendate: "description nouvelle et augmentée de la Terre corrigées pour l'utilisation de la navigation») montrent qu'il a été expressément conçu pour l'utilisation de la navigation maritime . Bien que la méthode de construction ne est pas expliqué par l'auteur, Mercator a probablement utilisé une méthode graphique, le transfert de certaines lignes de rhumb préalablement tracées sur un globe à un carré graticule, puis régler l'espacement entre les parallèles de sorte que les lignes droites sont devenus, faisant le même angle avec les méridiens comme dans le monde entier.
Le développement de la projection de Mercator représenté une percée majeure dans la cartographie nautique du 16ème siècle. Cependant, il était en avance sur son temps, puisque les vieilles techniques de navigation et de levés ne étaient pas compatibles avec son utilisation dans la navigation. Deux problèmes principaux ont empêché son application immédiate: l'impossibilité de déterminer la longitude en mer avec une précision suffisante et le fait que directions magnétiques, au lieu de directions géographiques, ont été utilisés dans la navigation. Seulement dans le milieu du 18e siècle, après la chronomètre de marine a été inventé et la distribution spatiale des déclinaison magnétique a été connu, pourrait la projection de Mercator être pleinement adopté par les navigateurs.
Plusieurs auteurs sont associés au développement de la projection Mercator:
- Allemand Erhard Etzlaub (c. 1460-1532), qui avait gravé miniatures "compas cartes" (environ 10x8 cm) de l'Europe et certaines régions d'Afrique, les latitudes 67 ° -0 °, pour permettre l'ajustement de ses cadrans solaires portables de poche, était pour décennies déclaré avoir conçu "une projection identique à Mercator de". Ce est depuis avéré être une erreur, remontant à la recherche doubtable en 1917.
- Mathématicien portugais et cosmographe Pedro Nunes (1502-1578), qui a décrit l'loxodrome et son utilisation dans la navigation maritime, et a suggéré la construction de plusieurs cartes marines à grande échelle dans la projection cylindrique équidistante de représenter le monde avec une distorsion d'un angle minimal (1537).
- Mathématicien anglais Edward Wright (c. 1558-1615), qui a formalisé les mathématiques de la projection de Mercator (1599), et publié tables précises pour sa construction (1599, 1610).
- Mathématiciens anglais Thomas Harriot (1560-1621) et Henry Bond (c.1600-1678) qui, indépendamment (c. 1600 et 1645), associé avec la projection de Mercator sa formule logarithmique moderne, plus tard déduit par le calcul.
Mathématiques de la projection

Les équations suivantes déterminent le x et y les coordonnées d'un point sur une carte Mercator de sa latitude et φ longitude λ (avec λ 0 étant la longitude dans le centre de la carte):
Ce est l'inverse de la Fonction de Gudermann:
Ceci est le Fonction de Gudermann:
L'échelle est proportionnelle à la sécante de l'φ de latitude, se arbitrairement grand près de la pôles, où φ = ± 90 °. En outre, comme le montrent les formules, y du pôle est plus ou moins l'infini.
Dérivation de la projection

Supposons une Terre sphérique. (Ce est en fait légèrement aplati, mais à petite échelle maps la différence est négligeable. Pour plus de précision, interposer conforme latitude .) Nous cherchons une transformée de longitude-latitude (λ, φ) à cartésien (x, y) qui est "un cylindre tangent à l'équateur" (ce est à dire x = λ) et conforme, de telle sorte que :
De x = λ nous obtenons
donnant
Ainsi y est une fonction de φ seulement avec  à partir de laquelle un table des intégrales donne
à partir de laquelle un table des intégrales donne
Il est commode de la carte φ = 0 à y = 0, afin de prendre C = 0.
Utilisations
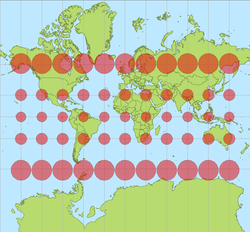
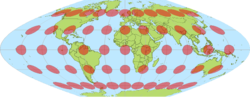
Comme toutes les projections cartographiques qui tentent de se adapter à une surface courbe sur une feuille plate, la forme de la carte est une déformation de la véritable mise en page de la surface de la Terre. La projection de Mercator exagère la taille des zones loin de l' équateur . Par exemple:
- Groenland est présenté comme ayant à peu près autant de superficie que l'Afrique , alors qu'en fait, la zone de l'Afrique est d'environ 14 fois supérieure à celle du Groenland.
- Alaska est présenté comme ayant une plus grande superficie de terres similaires ou même légèrement que le Brésil , où la zone du Brésil est en fait plus de cinq fois supérieure à celle de l'Alaska.
- La Finlande est présenté comme ayant une plus grande mesure Nord-Sud comme l'Inde , lorsque cette distance est beaucoup plus grande en Inde que la Finlande.
Bien que la projection de Mercator est encore d'usage courant pour la navigation, en raison de ses propriétés uniques, les cartographes conviennent qu'il ne est pas adapté à représenter le monde entier dans des publications ou des cartes murales en raison de sa déformation de la surface terrestre. Mercator se utilisé l'égalité de zone projection sinusoïdale pour montrer domaines relatifs. A la suite de ces critiques, moderne atlas ne utilisent plus la projection de Mercator pour les cartes du monde ou pour les zones éloignées de l'équateur, préférant d'autres projections cylindriques , ou formes de projection équivalente . La projection de Mercator est encore couramment utilisée pour les zones près de l'équateur, cependant, où la distorsion est minime.
Arno Peters a suscité la controverse quand il a proposé ce qui est connu sous le nom Projection de Peters , une légère modification de la projection cylindrique équivalente Lambert-salon, comme l'alternative à l'Mercator. Une résolution de 1989 par sept groupes géographiques Amérique du Nord a dénoncé l'utilisation de toutes les cartes rectangulaires de coordonnées monde, y compris le Mercator et Peters-Gall.
Google Maps utilise actuellement une projection Mercator pour ses images cartographiques. Malgré ses relatifs distorsions d'échelle, le Mercator est bien adapté comme une carte du monde interactive qui peut être déplacé et zoomé de manière transparente à des cartes locales. (Google Satellite Maps, d'autre part, a utilisé une projection plaque carrée jusqu'au 2005-07-22 .)
Le Google Maps maximale φ de latitude se produit à ± 85,05113 degrés lorsque l'Mercator valeur y = π. Ou plus précisément: