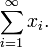Séquence

Pour les autres sens de ce mot, voir

En mathématiques , une séquence est une liste ordonnée d'objets (ou des événements). Comme un ensemble, il contient membres (aussi appelés éléments ou des termes), et le nombre de termes (éventuellement infinie) est appelée la longueur de la séquence. Contrairement à un ensemble, commandez questions, et exactement les mêmes éléments peuvent apparaître plusieurs fois à différentes positions dans la séquence.

Par exemple, (C, R, Y) est une séquence de lettres qui diffère de (Y, C, R), comme les points de commande. Les séquences peuvent être finis, comme dans cet exemple, ou infini , telle que la séquence de toutes même positifs entiers (2, 4, 6, ...).

Une suite infinie de nombres réels (en bleu). Cette séquence ne est ni augmentation ni diminution, ni convergente. Il est toutefois limité.

Exemples et notation

Il existe différents et assez différentes notions de séquences en mathématiques, dont certains] ct une séquence est un conteneur de taille variable dont les éléments sont disposés dans un ordre strictement linéaire. Il prend en charge l'insertion et l'enlèvement des éléments. Raffinement de l'avant Container, par défaut constructible Associated types Aucune, sauf pour celles de l'avenir Container. Notation type XA qui est un modèle de la séquence a, b objet de type XT Le type de X t objet de type T p de valeur, q objet de type X :: iterator n objet d'un type convertible à X :: size_type

Définitions Si a est une séquence, alors p est un itérateur valide dans un si ce est un itérateur valide (non singulière) qui est accessible à partir de a.begin (). Si a est une séquence, puis [p, q) est une plage valide en un si p et q sont valides dans une itérateurs et si q est accessible à partir de la p.

Les expressions valides n'êtes pas couverts par les notations introduites ci-dessous.

Une séquence peut être notée (a _1, a _2, ...). Pour la brièveté, la notation (a _n) est également utilisé.

Une définition plus formelle d'une séquence finie avec des termes dans un un ensemble S est fonction de {1, 2, ..., n} de S pour un certain n ≥ 0. Une séquence infinie en S est une fonction à partir de {1, 2, ...} (l'ensemble des nombres naturels sans 0) à S.

Séquences peuvent également commencent à partir de 0, de sorte que le premier terme de la séquence est alors un _0.

Une séquence d'une longueur fixe n est appelé également un n -uple. Suites finies comprennent la séquence vide () qui n'a pas d'éléments.

Une fonction de tous les entiers en un ensemble est parfois appelé une séquence bi-infini, car il peut être considéré comme une séquence indexé par des entiers négatifs greffés sur une séquence indexé par des nombres entiers positifs.

Types et propriétés des séquences

Un sous-séquence d'une séquence donnée est une séquence formée à partir de la séquence donnée en supprimant certains des éléments sans déranger les positions relatives des éléments restants.

Si les termes de la suite sont un sous-ensemble d'un ensemble ordonné, puis une séquence croissante monotone est une pour laquelle chaque terme est supérieure ou égale à la durée avant; si chaque terme est strictement supérieur à celui qui le précède, la séquence est appelée strictement monotone croissante. Une séquence monotone décroissante est définie de manière similaire. Ne importe quelle séquence remplir la propriété de monotonie est appelé monotone ou monotone. Ce est un cas particulier de la notion plus générale de fonction monotone.

Les termes non décroissante et non croissante sont utilisés afin d'éviter toute confusion possible avec strictement croissante et strictement décroissante, respectivement. Si les termes d'une séquence sont des nombres entiers , alors la séquence est un séquence entier. Si les termes d'une séquence sont des polynômes , alors la séquence est un séquence polynomiale.

Si S est doté d'une topologie , il devient alors possible d'envisager une convergence d'une suite infinie de S. Ces considérations impliquent le concept de la limite d'une suite.

Séquences d'analyse

Dans l'analyse , quand on parle de séquences, on tient généralement compte des séquences de la forme

ou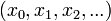

ce est à dire, des séquences infinies d'éléments indexés par les nombres naturels .

Il peut être commode d'avoir la séquence commence avec un indice différent de 1 ou 0. Par exemple, la séquence définie par x _n = 1 / log (n) serait défini que pour n ≥ 2. Quand on parle de telles séquences infinies, il suffit généralement (et ne change pas beaucoup pour la plupart des considérations) de supposer que les membres de la séquence sont définies au moins pour tous les indices assez grand, ce est-supérieure à une certaine N donné.)

Le type le plus élémentaire de séquences sont ceux numériques, ce est-séquences de réels ou des nombres complexes . Ce type peut être généralisée à des séquences d'éléments de certains espace vectoriel . Dans l'analyse, les espaces vectoriels considérés sont souvent espaces fonctionnels. Plus généralement encore, on peut étudier les séquences d'éléments dans une certaine espace topologique.

Série

La somme des termes d'une suite est une série. Plus précisément, si (x _1, x _2, x _3, ...) est une séquence, on peut considérer la séquence de sommes partielles (S _1, S _2, S _3, ...), avec

Formellement, cette paire de séquences comprend la série des termes x _1, x _2, x _3, ..., qui est désignée comme

Si la séquence de sommes partielles est convergente, on utilise aussi la notation de somme infinie pour sa limite. Pour plus de détails, voir série.

Séquences infinies dans l'informatique théorique

Séquences infinies de chiffres (ou caractères) tirés d'une fini alphabet sont d'un intérêt particulier dans informatique théorique. Ils sont souvent désignés simplement sous forme de séquences (par opposition à finies cordes). Séquences binaires infinis, par exemple, sont des séquences infinies de bits (personnages tirés de l'alphabet {0,1}). L'ensemble C = {0, 1} ^∞ de tous, des séquences binaires infinis est parfois appelé le Espace de Cantor.

Une séquence binaire infinie peut représenter une langage formel (un ensemble de chaînes) en réglant le n ième bit de la séquence à 1 si et seulement si le n ième chaîne (en Afin shortlex) est dans la langue. Par conséquent, l'étude de classes de complexité, qui sont des ensembles de langues, peuvent être considérés comme l'étude des ensembles de séquences infinies.

Une séquence infinie tirée de l'alphabet {0, 1, ..., b-1} peut aussi représenter un nombre réel exprimé dans la base-b système de numération positionnel. Cette équivalence est souvent utilisé pour amener les techniques de analyse réelle à porter sur les classes de complexité.

Les séquences en tant que vecteurs

Séquences sur un corps peuvent également être considérés comme des vecteurs dans un espace vectoriel . Plus précisément, l'ensemble de séquences à valeurs F (où F est un terrain) est un espace de fonction (en fait, un espace de produit) de F à valeurs fonctions sur l'ensemble des nombres naturels.

En particulier, le terme l'espace de séquence se réfère généralement à un sous-espace linéaire de l'ensemble de toutes les séquences possibles avec les infinite éléments == séquences doublement infinite == Normalement, la séquence infinie terme se réfère à une séquence qui est infini dans une direction, et fini à l'autre - la séquence présente un premier élément, mais pas d'élément final (une séquence de liaisons simples infinie). Une séquence doublement infini est infinie dans les deux sens - il n'a ni une première ni un élément final. Singly-séquences infinies sont fonctions des nombres naturels (n ') à un ensemble, alors que les séquences doublement infinies sont fonctions des entiers (Z) pour un certain ensemble.

On peut interpréter individuellement séquences infinies comme élément de la anneau de semi-groupe des nombres naturels et des séquences doublement infinite que les éléments de la anneau de groupe des entiers . Ce point de vue est utilisé dans le Cauchy produit de séquences.

Séquence ordinale indexés

Une Module: Order_topology ( parler · · hist · · liens · sous-pages essais - résultats) est une généralisation d'une séquence. Si α est un ordinal limite et X est un ensemble, une séquence d'éléments de X-α indexées est une fonction de α à X. Dans cette terminologie une séquence d'ω-indexé est une séquence ordinaire.

Séquences et automates

Automates ou machines à états finis peuvent généralement pensé graphiques comme dirigés, avec des bords marqués en utilisant un alphabet Σ spécifique. Types plus familiers de la transition des automates d'un état à en lisant des lettres d'entrée de Σ, à la suite bords avec des étiquettes correspondant; l'entrée commandé pour un tel automate forme une séquence appelée un mot (ou mot d'entrée). La séquence d'états rencontrés par l'automate lors du traitement un mot est appelé une course. Un automate non déterministe peut avoir non marqué ou dupliquer sur-bords pour un Etat, donnant plus d'un successeur pour une lettre saisie. Cela est généralement considéré comme produisant plusieurs pistes possibles pour un mot donné, chacune étant une séquence d'états simples, plutôt que de produire un seul passage qui est une séquence d'ensembles d'états; Toutefois, «run» est parfois utilisé pour désigner ce dernier.