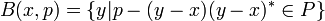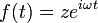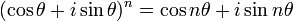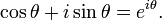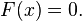Nombre complexe
À propos de ce écoles sélection Wikipedia
Les articles de cette sélection écoles ont été organisés par sujet du programme d'études grâce aux bénévoles d'enfants SOS. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...

En mathématiques , un nombre complexe est un nombre qui peut être formellement définie comme une paire de ordonné nombres réels (a, b), souvent écrit:
où i 2 = -1.
Les nombres complexes ont addition, la soustraction, la multiplication et de la division des opérations définies, avec des comportements qui sont un sur-ensemble strict de nombres réels, ainsi que d'avoir d'autres propriétés élégantes et utiles. Notamment, les nombres réels négatifs peuvent être obtenus en élevant au carré les nombres complexes.
Les nombres complexes ont été inventés quand il a été découvert que la résolution de certains équations cubiques doivent calculs intermédiaires contenant les racines carrées des nombres négatifs, même lorsque les solutions finales ont été nombres réels. En outre, à partir de la théorème fondamental de l'algèbre, l'utilisation des nombres complexes comme le champ de numéro pour polynômes équations algébriques signifie que des solutions existent toujours. L'ensemble des nombres complexes former un algébriquement clos champ, à la différence de l'ensemble des nombres réels, qui ne est pas algébriquement clos.
Les nombres complexes sont utilisés dans de nombreux domaines différents, y compris des applications dans l'ingénierie , l'électromagnétisme , la physique quantique , les mathématiques appliquées , et la théorie du chaos . Lorsque le champ sous-jacent de nombres d'un type de mathématiques est le champ de nombres complexes, le nom reflète généralement ce fait. Des exemples sont analyse complexe, la matrice complexe , polynomiale complexe et algèbre de Lie complexe.
Définitions
Notation
Bien que d'autres notations peuvent être utilisés, les nombres complexes sont très souvent écrits sous la forme
où a et b sont des nombres réels et i est l' unité imaginaire , qui a la propriété i 2 = -1. Le nombre réel a est appelé la partie réelle du nombre complexe, et le nombre réel b est la partie imaginaire .
Les nombres réels peuvent être exprimés en nombres complexes avec la partie imaginaire de zéro; qui est, le nombre réel a est équivalent au nombre complexe a 0 i. Les nombres complexes avec une partie réelle qui est nulle sont appelés nombres imaginaires.
Par exemple, 3 + 2 i est un nombre complexe, avec une partie réelle et la partie imaginaire 3 2. Si z = a + ib, la partie réelle (a) est notée Re (z) ou  Et la partie imaginaire (b) est notée Im (Z) ou
Et la partie imaginaire (b) est notée Im (Z) ou 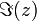 .
.
Dans certaines disciplines (en particulier, le génie électrique , où i est un symbole pour actuelle), l' unité imaginaire i est écrit au lieu que j, donc les nombres complexes sont parfois écrites comme + jb.

f (x) = (x ²-1) (x -2- i) ² /
(X ² + 2 + 2 i). La teinte représente l'argument de la fonction, tandis que la saturation représente l'ampleur.
Le ensemble des nombres complexes est généralement désigné par C, ou tableau noir gras par 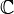 . Les nombres réels, R, peuvent être considérées comme un sous-ensemble de C en considérant tout nombre réel comme un complexe: A = A + 0 i.
. Les nombres réels, R, peuvent être considérées comme un sous-ensemble de C en considérant tout nombre réel comme un complexe: A = A + 0 i.
Égalité
Deux nombres complexes sont égaux si et seulement si les parties réelles sont égales et leurs parties imaginaires sont égales. Ce est, a + c = bi + di si et seulement si a = c et b = d.
Opérations
Les nombres complexes sont additionnées, soustraites, multipliées, et divisés en appliquant formellement le associative , commutative et lois de l'algèbre de distribution, ainsi que l'équation i 2 = -1:
- Addition:

- Soustraction:

- Multiplication:

- Division:

- Addition:
(Division des nombres complexes est encore défini ultérieurement).
Le champ de nombres complexes
Formellement, les nombres complexes peuvent être définis en tant que couples de nombres réels (a, b) ainsi que les opérations:
Ainsi défini, les nombres complexes forment un champ, le champ de nombre complexe, notée C (un champ est une structure algébrique dans laquelle addition, soustraction, multiplication et division sont définies et répondent à certaines lois algébriques. Par exemple, les nombres réels forment un champ).
Le nombre réel est identifié par un nombre complexe (a, 0), et de cette façon le champ de nombres réels R devient un sous-corps de C. L' unité imaginaire i peut alors être définie comme le nombre complexe (0, 1), qui vérifie
En C, nous avons:
- identité additif («zéro»): (0, 0)
- identité multiplicative ("un"): (1, 0)
- inverse additif de (a, b): (- a, - b)
- inverse multiplicatif (réciproque) de non-zéro (a, b):
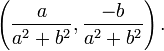
Depuis un certain nombre complexe a + bi est spécifiée de manière unique par un couple (A, B) de nombres réels, des nombres complexes sont en une-à-une correspondance avec des points sur un plan, appelé le plan complexe .
C peut également être définie comme étant la fermeture topologique du nombres algébriques ou que le clôture algébrique de R, qui sont tous deux décrits ci-dessous.
Le plan complexe

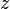 et son conjugué
et son conjugué  dans le plan complexe.
dans le plan complexe. Un nombre complexe z peut être considérée comme un point ou un vecteur de position dans un à deux dimensions du système de coordonnées cartésiennes appelé le plan complexe ou Argand diagramme (nommé d'après Jean-Robert Argand) - voir figure à droite. Le point et donc le nombre complexe z peuvent être spécifiés par cartésienne (rectangulaire) coordonnées. Les coordonnées cartésiennes du nombre complexe sont la partie réelle x = Re (z) et la partie imaginaire y = Im (z). La représentation d'un nombre complexe par ses coordonnées cartésiennes est appelée la forme cartésienne ou la forme rectangulaire ou forme algébrique de ce nombre complexe.
Valeur absolue, la conjugaison et la distance
La valeur absolue (ou module) ou amplitude d'un nombre complexe 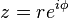 est défini comme étant
est défini comme étant  . Algébriquement, si
. Algébriquement, si  , Puis
, Puis 
On peut vérifier facilement que la valeur absolue a trois propriétés importantes:
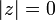 si et seulement si
si et seulement si 
 ( inégalité triangulaire)
( inégalité triangulaire)
pour tous les nombres complexes z et w. Il se ensuit donc, par exemple, que  et
et  . En définissant la fonction de distance
. En définissant la fonction de distance  nous nous tournons l'ensemble des nombres complexes dans un espace métrique et nous pouvons donc parler de limites et la continuité.
nous nous tournons l'ensemble des nombres complexes dans un espace métrique et nous pouvons donc parler de limites et la continuité.
Le complexe conjugué du nombre complexe  est défini comme étant
est défini comme étant 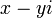 , Écrit
, Écrit  ou
ou  . Comme on le voit sur la figure,
. Comme on le voit sur la figure,  est le «reflet» de z sur l'axe réel. Ce qui suit peut être vérifié:
est le «reflet» de z sur l'axe réel. Ce qui suit peut être vérifié:
 si et seulement si z est réel
si et seulement si z est réel
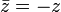 si et seulement si z est purement imaginaire
si et seulement si z est purement imaginaire
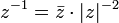 si z est différent de zéro.
si z est différent de zéro.
Cette dernière formule est la méthode de choix pour calculer l'inverse d'un nombre complexe si elle est donnée en coordonnées rectangulaires.
Qui commute de conjugaison avec toutes les opérations algébriques (et de nombreuses fonctions; par exemple,  ) Est enracinée dans l'ambiguïté dans le choix de i (-1 a deux racines carrées). Il est important de noter, cependant, que la fonction
) Est enracinée dans l'ambiguïté dans le choix de i (-1 a deux racines carrées). Il est important de noter, cependant, que la fonction 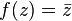 ne est pas complexe différentiable (voir fonction holomorphe).
ne est pas complexe différentiable (voir fonction holomorphe).
Fractions complexes
Nous pouvons diviser un nombre complexe (a + bi) par un autre nombre complexe (c + di) ≠ 0 de deux façons. La première a déjà été implicite: pour convertir les deux nombres complexes sous forme exponentielle, à partir de laquelle leur quotient est facilement déduite. La deuxième façon consiste à exprimer la division comme une fraction, puis de multiplier le numérateur et le dénominateur par le conjugué complexe du dénominateur. Le nouveau dénominateur est un nombre réel.
Interprétation géométrique des opérations sur les nombres complexes

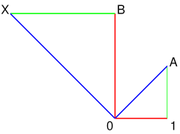
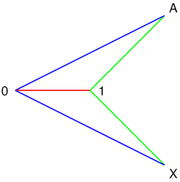
Considérons un avion . Un point est à l'origine, 0. Un autre point est l'unité, ou 1.
La somme des deux points A et B est le point X = A + B de telle sorte que les triangles dont les sommets 0, A, B et X, B, A, sont congruents.
Le produit de deux points A et B est le point X = AB de telle sorte que les sommets des triangles avec 0, 1, A et 0, B, X, sont similaire.
Le conjugué complexe d'un point A est le point X = A * tel que les sommets des triangles avec 0, 1, A, et 0, 1, X, sont des images spéculaires l'une de l'autre.
Cette interprétation géométrique permet problèmes de géométrie à être traduits en algèbre. Le problème de la construction géométrique de la 17-gon se traduit donc dans l'analyse de l'équation algébrique x 17 = 1.
Forme polaire
En variante à la représentation cartésienne z = x + iy, le nombre complexe z peut être spécifiée en coordonnées polaires . Les coordonnées polaires sont r = | z | ≥ 0, dite valeur absolue ou module et φ = arg (z), appelé l'argument ou l'angle de z. Pour r = 0 ne importe quelle valeur de φ décrit le même numéro. Pour obtenir une représentation unique, un choix classique est de mettre en arg (0) = 0. Pour r> 0 l'argument φ est unique modulo 2π; qui est, si deux valeurs de l'argument complexe diffèrent par une exacte nombre entier multiple de 2π, ils sont considérés comme équivalents. Pour obtenir une représentation unique, un choix classique consiste à φ limiter à l'intervalle (-π, π], ce est à dire -π <φ ≤ π. La représentation d'un nombre complexe par ses coordonnées polaires est appelée la forme polaire du nombre complexe .
Conversion de la forme polaire à la forme cartésienne
Conversion de la forme cartésienne à la forme polaire
(Voir arg et fonction atan2.)
La valeur obtenue pour φ est dans la gamme (-π, + π];. Il est négatif pour les valeurs négatives de y Si les valeurs à la place non-négatives dans l'intervalle [0, 2π) sont souhaitées, ajouter 2π à des résultats négatifs.
Notation de la forme polaire
La notation de la forme polaire
est appelé forme trigonométrique. Le φ notation cis est parfois utilisé comme une abréviation pour cos φ + i sin φ. Utilisation La formule d'Euler il peut aussi se écrire
qui est appelé forme exponentielle.
Multiplication, division, exponentiation, et l'extraction de la racine dans la forme polaire
Multiplication, division, exponentiation, et l'extraction des racines sont beaucoup plus faciles dans la forme polaire que dans la forme cartésienne.
Utilisation somme et la différence des identités son possible pour obtenir que
et cela
Exponentiation avec exposants entiers; selon La formule de De Moivre,
Exponentiation avec des exposants complexes arbitraires est discutée dans l'article sur exponentiation .
L'addition de deux nombres complexes ne est que la somme vectorielle de deux vecteurs, et la multiplication par un nombre complexe fixe peut être considéré comme une rotation et d'étirage simultané.
La multiplication par i correspond à une rotation dans le sens antihoraire de 90 degrés (π / 2 radians ). Le contenu géométrique de l'équation i 2 = -1 est qu'une séquence de deux rotations de 90 degrés résultats à un degré 180 (π radians) de rotation. Même le fait (-1) · (-1) = 1 de l'arithmétique peut être compris géométriquement comme la combinaison de deux virages à 180 degrés.
Toutes les racines de ne importe quel nombre, réel ou complexe, peuvent être trouvés avec un simple algorithme . La n-ième racines sont donnés par
pour k = 0, 1, 2, ..., n - 1, où ![\ Sqrt [n] {r}](../../images/145/14548.png) représente le principal n ième racine de r.
représente le principal n ième racine de r.
Certaines propriétés
Représentation matricielle des nombres complexes
Bien que généralement pas utile, des représentations alternatives du domaine complexe peuvent donner une idée de sa nature. Une représentation particulièrement élégante interprète chaque nombre complexe comme une 2 × 2 matrice avec de vraies entrées qui se étend et tourne les points du plan. Chaque telle matrice a la forme
où a et b sont des nombres réels. La somme et le produit de deux de ces matrices est à nouveau de cette forme, et l'opération de produit sur des matrices de cette forme est commutative . Chaque matrice non-zéro de ce formulaire est inversible et son inverse est nouveau de ce formulaire. Par conséquent, les matrices de cette forme sont un terrain, isomorphe au champ de nombres complexes. Chaque telle matrice peut se écrire
ce qui suggère que nous devrions identifier le véritable numéro 1 avec la matrice d'identité
et i l'unité imaginaire avec
une rotation dans le sens antihoraire de 90 degrés. Notez que le carré de cette dernière matrice est en effet égale à la matrice 2 × 2 qui représente -1.
Le carré de la valeur absolue d'un nombre complexe exprimé sous forme de matrice est égal au déterminant de cette matrice.
Si la matrice est considérée comme une transformation de l'avion, puis la transformation des points tourne d'un angle égal à l'argument du nombre complexe et échelles par un facteur égal à la valeur absolue du nombre complexe. Le conjugué du nombre complexe z correspond à la transformation qui fait tourner par l'intermédiaire du même angle que z mais dans la direction opposée, et les échelles de la même manière que z; cela peut être représenté par la transposée de la matrice correspondant à z.
Si les éléments de matrice sont eux-mêmes nombres complexes, l'algèbre obtenue est celle de la quaternions. En d'autres termes, cette représentation matricielle est une façon d'exprimer la La construction de Cayley-Dickson d'algèbres.
Il convient également de noter que les deux valeurs propres de la matrice de 2x2 représentant un nombre complexe sont le nombre complexe lui-même et de son conjugué.
Espace vectoriel réel
C est un vrai deux dimensions espace vectoriel . Contrairement aux réels, l'ensemble des nombres complexes ne peut pas être totalement ordonné d'une façon qui est compatible avec ses opérations arithmétiques: C ne peut pas être transformé en un corps ordonné. Plus généralement, aucun champ contenant une racine carrée de -1 peut être commandé.
Cartes -linéaire R C → C ont la forme générale
à coefficients complexes a et b. Seul le premier terme est C-linéaires, et seul le premier terme est holomorphe; le second terme est réel différentiables, mais ne satisfait pas le Équations de Cauchy-Riemann.
La fonction
correspond à des rotations combinées avec mise à l'échelle, tandis que la fonction
correspond à des réflexions combinées avec mise à l'échelle.
Les solutions d'équations polynomiales
A la racine du polynôme p est un nombre complexe z de telle sorte que p (z) = 0. Un résultat surprenant dans l'analyse complexe est que tous les polynômes de degré n à coefficients réels ou complexes ont des racines complexes exactement n (comptage racines multiples en fonction de leur multiplicité). Ceci est connu comme la théorème fondamental de l'algèbre, et il montre que les nombres complexes sont un corps algébriquement clos.
En effet, le champ de nombre complexe C est la clôture algébrique du champ de nombre réel, et Cauchy construit le domaine des nombres complexes de cette manière. Il peut également être caractérisé comme le anneau quotient du polynôme anneau R [X] sur le idéal engendré par le polynôme X ² + 1:
Ce est en effet un champ parce que X ² + 1 est irréductible, d'où la génération d'un idéal maximal, dans la R [X]. L'image de X dans cet anneau de quotient est l'unité imaginaire i.
Algébrique caractérisation
Le champ C est ( jusqu'à terrain isomorphisme) caractérisé par les trois faits suivants:
- son caractéristique est 0
- son degré de transcendance sur la corps premier est le cardinalité du continuum
- il est algébriquement clos
Par conséquent, C contient de nombreux sous-champs qui sont propres isomorphe à C. Une autre conséquence de cette caractérisation est que le Groupe de Galois de C sur les nombres rationnels est énorme, de cardinal égal à celle de l'ensemble du continuum de puissance.
Caractérisation comme un champ topologique
Comme indiqué plus haut, la caractérisation algébrique de C ne rend pas compte de certaines de ses propriétés les plus importantes. Ces propriétés, qui sous-tendent les fondements de analyse complexe, résultent de la topologie de C. Les propriétés suivantes caractérisent en C champ topologique:
- C est un champ.
- C contient un sous-ensemble d'éléments non nuls P satisfaisants:
- P est fermé pour l'addition, la multiplication et prenant inverses.
- Si x et y sont des éléments distincts de P, alors soit xy ou yx est à P
- Si S est tout sous-ensemble non vide de P, alors S + P = x + P pour certains x dans C.
- C a un automorphisme involutif non trivial x → x *, fixant P et tel que xx * est en P pour tout x non nuls dans C.
Compte tenu de ces propriétés, on peut alors définir une topologie sur C en prenant les séries
comme un base, où x parcourt C, et p gammes sur P.
Pour voir que ces propriétés caractérisent C comme champ topologique, on constate que P ∪ {0} ∪ -P est un ordonné Champ Dedekind-complète, et donc peuvent être identifiés avec le nombres réels R par un isomorphisme de champ unique. La dernière propriété est facilement visible impliquer que le Groupe de Galois sur les nombres réels est d'ordre deux, complétant la caractérisation.
Pontriaguine a montré que la seule lié localement compact champs topologiques sont R et C. Cela donne une autre caractérisation de C comme un champ topologique, puisque C peut être distinguée de R en notant que les nombres complexes non nuls connecté, tandis que les nombres réels non nuls ne sont pas.
Analyse complexe
L'étude des fonctions d'une variable complexe est connu comme analyse complexe et a un énorme utilisation pratique dans les mathématiques appliquées ainsi que dans d'autres branches des mathématiques. Souvent, les preuves les plus naturels pour les déclarations en analyse réelle ou même la théorie des nombres emploient des techniques de l'analyse complexe (voir théorème des nombres premiers pour un exemple). Contrairement fonctions réelles qui sont couramment représentés comme deux dimensions graphiques, fonctions complexes ont quatre dimensions graphiques et peuvent utilement être illustrés par un codage couleur trois dimensions graphique de proposer quatre dimensions, ou en animant transformation dynamique de la fonction complexe du plan complexe.
Applications
Les mots "réels" et "imaginaires" étaient sens quand les nombres complexes ont été utilisés principalement comme une aide dans la manipulation de chiffres «réels», avec seulement la partie «réel» décrivant directement le monde. Des applications plus tardives, et en particulier la découverte de la mécanique quantique, a montré que la nature n'a pas de préférence pour les nombres «réels» et ses plus réel descriptions exigent souvent des nombres complexes, la partie «imaginaire» étant tout aussi physique que la partie «réel».
La théorie du contrôle
Dans la théorie du contrôle , les systèmes sont souvent transformés de la dans le domaine temporel à la domaine de fréquence en utilisant la Transformée de Laplace. Le système de pôles et les zéros sont ensuite analysés dans le plan complexe. Le lieu des racines, Diagramme de Nyquist, et Techniques de l'intrigue Nichols font toute utilisation du plan complexe.
Dans le procédé de lieu des pôles, il est particulièrement important si le pôles et zéros sont dans les plans de moitié gauche ou à droite, ce est à dire avoir une véritable partie supérieure ou inférieure à zéro. Si un système a des pôles qui sont
- dans le demi-plan droit, il sera instable,
- tous dans le demi-plan gauche, il sera stable,
- sur l'axe imaginaire, elle aura stabilité marginale.
Si un système a des zéros dans le demi-plan droit, ce est un système de phase nonminimum.
Analyse des signaux
Les nombres complexes sont utilisés dans l'analyse du signal et d'autres domaines pour une description commode pour les signaux variant périodiquement. Pour les fonctions indiquées représentant quantités physiques réelles, souvent en termes de sinus et cosinus, les fonctions complexes correspondant sont considérés dont les parties réelles sont les quantités originales. Pour un onde sinusoïdale d'une donnée la fréquence, la valeur absolue | z | z de la correspondante est la amplitude et l'argument arg (z) le phase.
Si L'analyse de Fourier est utilisée pour écrire un signal de valeur réelle donnée comme une somme de fonctions périodiques, ces fonctions périodiques sont souvent écrites comme des fonctions de valeurs complexes de la forme
où ω représente la la fréquence angulaire et du nombre complexe z code pour la phase et l'amplitude, comme expliqué ci-dessus.
En génie électrique , le Transformée de Fourier est utilisée pour analyser divers tensions et courants. Le traitement de des résistances, condensateurs, et inductances peuvent être unifiés par l'introduction, les résistances dépendant de la fréquence imaginaires de ces deux derniers et à combiner tous les trois dans un seul nombre complexe appelé le impédance. (Ingénieurs électriques et certains physiciens utilisent la lettre j pour l'unité imaginaire depuis i est généralement réservée aux courants divers et peuvent entrer en conflit avec i.) Cette approche est appelée calcul phaseur. Cette utilisation est aussi étendue à traitement numérique du signal et traitement d'image numérique, qui utilisent des versions numériques de l'analyse de Fourier (et Analyse en ondelettes) pour transmettre, comprimer, restaurer et contraire processus numériques audio signaux, d'images fixes, et signaux vidéo.
Intégrales impropres
Dans les domaines appliqués, les nombres complexes sont souvent utilisés pour calculer certaines valeurs réelles intégrales impropres, au moyen de fonctions à valeurs complexes. Plusieurs méthodes existent pour ce faire; voir méthodes d'intégration de contour.
Mécanique quantique
Le champ de nombre complexe est pertinente dans le formulation mathématique de la mécanique quantique, où complexe Espaces de Hilbert fournissent le contexte pour une telle formulation qui est pratique et peut-être plus standard. Les formules de base d'origine de la mécanique quantique - la Schrödinger équation et Heisenberg mécanique matricielle - font usage des nombres complexes.
Relativité
Dans spéciale et la relativité générale , certaines formules pour la métrique sur espace-temps deviennent plus simples si l'on prend la variable de temps pour être imaginaire. (Ce ne est plus la norme.) Les nombres complexes sont essentiels pour spineurs qui sont une généralisation de la tenseurs utilisés dans la relativité.
Mathématiques appliquées
Dans les équations différentielles , il est fréquent de trouver d'abord toutes les racines complexes de la r équation caractéristique d'un équation différentielle linéaire et ensuite tenter de résoudre le système en termes de fonctions de base de la forme f (t) = e rt.
La dynamique des fluides
En la dynamique des fluides, des fonctions complexes sont utilisés pour décrire écoulement potentiel en deux dimensions.
Fractales
Certains fractales sont tracées dans le plan complexe par exemple ensemble de Mandelbrot et Ensemble de Julia.
Histoire
La première référence fugace racines carrées de nombres négatifs peut-être eu lieu dans le travail de la grecque mathématicien et inventeur Héron d'Alexandrie dans le 1er siècle après JC , quand il a examiné le volume d'un impossible tronc de pyramide , si les nombres négatifs ne ont pas été conçus dans le Monde hellénistique.
Les nombres complexes sont devenus plus importants dans le 16ème siècle , quand il est fermé formules pour les racines de cubique et quartiques polynômes ont été découverts par les mathématiciens italiens (voir Niccolo Fontana Tartaglia, Jérôme Cardan). Il est vite rendu compte que ces formules, même si l'on était seulement intéressé par des solutions réelles, parfois nécessaires la manipulation des racines carrées des nombres négatifs. Par exemple, la formule cube de Tartaglia donne la solution suivante à l'équation x ³ - x = 0:
À première vue, cela ressemble à un non-sens. Cependant calculs formels avec des nombres complexes montrent que l'équation z = i 3 a des solutions -i,  et
et  . En substituant à leur tour pour
. En substituant à leur tour pour 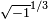 dans la formule cube de Tartaglia et en simplifiant, on obtient 0, 1 et -1 comme les solutions de x 3 - x = 0.
dans la formule cube de Tartaglia et en simplifiant, on obtient 0, 1 et -1 comme les solutions de x 3 - x = 0.
Ce était doublement troublante puisque même pas les nombres négatifs ont été considérés comme sur la terre ferme à l'époque. Le terme «imaginaire» pour ces quantités a été inventé par René Descartes 1637 et qui devait être dérogatoire (voir nombre imaginaire pour une discussion sur la «réalité» des nombres complexes). Une autre source de confusion est que l'équation  semblait être capricieusement incompatible avec l'identité algébrique
semblait être capricieusement incompatible avec l'identité algébrique  , Qui est valable pour réel positif nombres a et b, et qui a également été utilisé dans les calculs de nombres complexes avec l'un des a, b positif et l'autre négatif. L'utilisation incorrecte de cette identité (et l'identité liées
, Qui est valable pour réel positif nombres a et b, et qui a également été utilisé dans les calculs de nombres complexes avec l'un des a, b positif et l'autre négatif. L'utilisation incorrecte de cette identité (et l'identité liées  ) Dans le cas où a et b sont négatifs, même tourmenté Euler . Cette difficulté a finalement conduit à la convention d'utiliser le symbole spécial i à la place de
) Dans le cas où a et b sont négatifs, même tourmenté Euler . Cette difficulté a finalement conduit à la convention d'utiliser le symbole spécial i à la place de 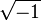 pour se prémunir contre cette erreur.
pour se prémunir contre cette erreur.
Le 18ème siècle a vu les travaux de Abraham de Moivre et Leonhard Euler . Pour de Moivre est due (1730) la formule bien connue qui porte son nom, la formule de de Moivre:
et à Euler (1748) La formule d'Euler de analyse complexe:
L'existence de nombres complexes ne était pas complètement accepté jusqu'à l'interprétation géométrique (voir ci-dessous) a été décrit par Caspar Wessel en 1799 ; il a été redécouvert quelques années plus tard et popularisé par Carl Friedrich Gauss , et par conséquent la théorie des nombres complexes a reçu une expansion notable. L'idée de la représentation graphique des nombres complexes était apparu, cependant, dès 1685, dans Le Tractatus de l'algèbre de Wallis.
Les mémoires de Wessel est apparu dans les Actes de la Copenhague Académie pour 1799, et est extrêmement claire et complète, même en comparaison avec des œuvres modernes. Il considère aussi que la sphère, et donne une la théorie de quaternion à partir de laquelle il développe une trigonométrie sphérique complète. En 1804, l'abbé Buée est venu de façon autonome la même idée qui Wallis avait suggéré, que  devrait représenter une ligne de l'unité, et son négatif, perpendiculaire à l'axe réel. Le document de buée ne fut publiée qu'en 1806, année où Jean-Robert Argand a également publié une brochure sur le même sujet. Il est à l'essai de Argand que la fondation scientifique pour la représentation graphique des nombres complexes est maintenant généralement appelé. Néanmoins, en 1831 Gauss trouvé la théorie tout à fait inconnu, et en 1832 a publié ses mémoires en chef sur le sujet, l'amenant ainsi en évidence devant le monde mathématique. Mention devrait également être faite d'un excellent petit traité par Mourey (1828), dans lequel les bases de la théorie des nombres directionnelles sont scientifiquement établi. L'acceptation générale de la théorie ne est pas un peu en raison de travaux de Augustin Louis Cauchy et Niels Henrik Abel, et surtout ce dernier, qui était le premier à utiliser hardiment nombres complexes avec un succès qui est bien connu.
devrait représenter une ligne de l'unité, et son négatif, perpendiculaire à l'axe réel. Le document de buée ne fut publiée qu'en 1806, année où Jean-Robert Argand a également publié une brochure sur le même sujet. Il est à l'essai de Argand que la fondation scientifique pour la représentation graphique des nombres complexes est maintenant généralement appelé. Néanmoins, en 1831 Gauss trouvé la théorie tout à fait inconnu, et en 1832 a publié ses mémoires en chef sur le sujet, l'amenant ainsi en évidence devant le monde mathématique. Mention devrait également être faite d'un excellent petit traité par Mourey (1828), dans lequel les bases de la théorie des nombres directionnelles sont scientifiquement établi. L'acceptation générale de la théorie ne est pas un peu en raison de travaux de Augustin Louis Cauchy et Niels Henrik Abel, et surtout ce dernier, qui était le premier à utiliser hardiment nombres complexes avec un succès qui est bien connu.
Les termes courants utilisés dans la théorie sont principalement due aux fondateurs. Argand appelé 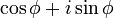 le facteur de direction, et
le facteur de direction, et  le module; Cauchy (1828) appelé
le module; Cauchy (1828) appelé 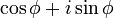 la forme réduite (l'expression Réduite); Gauss i utilisé pour
la forme réduite (l'expression Réduite); Gauss i utilisé pour 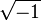 , A présenté le numéro de complexe terme pour
, A présenté le numéro de complexe terme pour 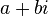 , Et a appelé
, Et a appelé  la norme.
la norme.
Le coefficient de direction d'expression, souvent utilisé pour 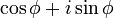 , Est due à Hankel (1867), et la valeur absolue, par module, est due à Weierstrass.
, Est due à Hankel (1867), et la valeur absolue, par module, est due à Weierstrass.
Après Cauchy et Gauss ont parcouru un nombre de contributeurs de haut rang, dont celui-ci peut être en particulier mentionné: Kummer (1844), Leopold Kronecker (1845), Scheffler (1845, 1851, 1880), Bellavitis (1835, 1852), Peacock (1845), et De Morgan (1849). Möbius doit également être mentionné pour ses nombreux mémoires sur les applications géométriques de nombres complexes, et Dirichlet pour l'expansion de la théorie des nombres premiers d'inclure, congruences, réciprocité, etc., comme dans le cas de nombres réels.
Un complexe anneau ou domaine est un ensemble de nombres complexes qui est fermé sous l'addition, la soustraction et la multiplication. Gauss étudié nombres complexes de la forme 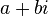 , Où a et b sont solidaires, ou rationnelle (et i est l'un des deux racines de
, Où a et b sont solidaires, ou rationnelle (et i est l'un des deux racines de  ). Son élève, Ferdinand Eisenstein, a étudié le type
). Son élève, Ferdinand Eisenstein, a étudié le type 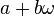 Où
Où 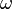 est une racine complexe de
est une racine complexe de 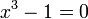 . Telles autres catégories (appelés corps cyclotomiques) de nombres complexes sont dérivées de la racines de l'unité
. Telles autres catégories (appelés corps cyclotomiques) de nombres complexes sont dérivées de la racines de l'unité  pour des valeurs supérieures de
pour des valeurs supérieures de  . Cette généralisation est largement dû à Kummer, qui a aussi inventé numéros idéales, qui ont été exprimés comme des entités géométriques par Felix Klein en 1893. La théorie générale des champs a été créé par Évariste Galois, qui a étudié les champs générés par les racines de toute équation polynomiale
. Cette généralisation est largement dû à Kummer, qui a aussi inventé numéros idéales, qui ont été exprimés comme des entités géométriques par Felix Klein en 1893. La théorie générale des champs a été créé par Évariste Galois, qui a étudié les champs générés par les racines de toute équation polynomiale
Les écrivains fin (de 1884) sur la théorie générale comprennent Weierstrass, Schwarz, Richard Dedekind, Otto Hölder, Bonaventure Berloty, Henri Poincaré, Eduard Study, et Alexander MacFarlane.
La définition formellement correcte en utilisant des paires de nombres réels a été donné dans le 19ème siècle .
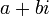












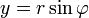
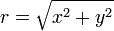




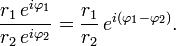
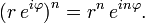
![\ Sqrt [n] {re ^ {i \ varphi}} = \ sqrt [n] {r} \ e ^ {i \ left (\ frac {\ varphi + 2k \ pi} {n} \ right)}](../../images/145/14547.png)

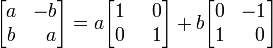

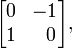




![\ Mathbb {C} = \ mathbb {R} [X] / (X ^ 2 + 1). \,](../../images/145/14557.png)