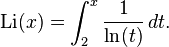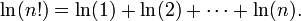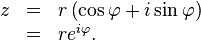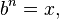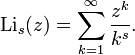Logarithme
À propos de ce écoles sélection Wikipedia
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Mères SOS chaque regard après une une famille d'enfants parrainés .

Le logarithme d'un nombre est l' exposant par lequel une autre valeur fixe, la de base, doit être soulevée pour produire ce nombre. Par exemple, le logarithme de base 10 de 1000 est 3, car 1000 est 10 à la puissance trois:. 1.000 = 10 x 10 x 10 = 3 10 Plus généralement, si x = b y, alors y est le logarithme de x à base b, et est écrit y = log b (x), donc log 10 (1000) = 3.
Le logarithme en base b = 10 est appelé logarithme commun et a de nombreuses applications en sciences et en génie. Le logarithme naturel a le e constante (≈ 2,718) que sa base; son utilisation est largement répandue dans mathématiques pures, en particulier le calcul . Le logarithme binaire utilise base b = 2 et est important dans la science informatique .
Logarithmes ont été introduites par John Napier dans le début du 17ème siècle comme un moyen de simplifier les calculs. Ils ont été rapidement adoptés par navigateurs, des scientifiques, des ingénieurs et d'autres pour effectuer des calculs plus facilement, à l'aide règles à calcul et tables de logarithmes. Étapes de multiplication à plusieurs chiffres fastidieuses peuvent être remplacés par consultation de tables hauts et plus simple en raison du fait - important dans son propre droit - que le logarithme d'un produit est le somme des logarithmes des facteurs:
La notion actuelle de logarithmes vient de Leonhard Euler , qui les reliée à la fonction exponentielle dans le 18ème siècle.
Les échelles logarithmiques réduire les quantités de vaste portée pour les petits télescopes. Par exemple, le décibel est une unité de quantification logarithmique les rapports de pression et de tension sonores. En chimie, Le pH est une mesure logarithmique de la acidité d'un solution aqueuse. Logarithmes sont monnaie courante dans scientifiques formules , et des mesures de la complexité des algorithmes et des objets géométriques appelé fractales . Ils décrivent intervalles musicaux, apparaissent dans les formules de comptage des nombres premiers , informer certains modèles psychophysique, et peuvent aider à juricomptabilité.
De la même manière que le logarithme inverse exponentiation , la logarithme complexe est la fonction inverse de la fonction exponentielle appliquée sur les nombres complexes . Le logarithme discret est une autre variante; elle trouve des applications dans cryptographie à clé publique.
Motivation et définition
L'idée de logarithmes est d'inverser le fonctionnement de exponentiation , qui soulève un certain nombre à une puissance. Par exemple, la troisième puissance (ou cube) de 2 est 8, parce que 8 est le produit de trois facteurs de 2:
Il se ensuit que le logarithme de 8 par rapport à la base 2 est 3, donc log 2 8 = 3.
Exponentiation
La troisième puissance de certains nombre b est le produit de trois facteurs de b. Plus généralement, b élever à la puissance n-ième de, où n est un nombre naturel , est effectuée en multipliant n facteurs de b. La puissance n ième de de b est écrit b n, de sorte que
Exponentation peut être étendue à y b, où b est un nombre positif et l'exposant y est tout nombre réel . Par exemple, b -1 est le inverse de b, ce est-1 / b.
Définition
Le logarithme d'un nombre x par rapport à la base b est l'exposant par lequel b doit être soulevée pour obtenir x. En d'autres termes, le logarithme de base b de x est la solution de l'équation y
Le logarithme est notée "log b (x)" (prononcé comme "le logarithme de x à la base b» ou «la base-b logarithme de x"). Dans l'équation y = log b (x), la valeur y est la réponse à la question «Pour quelle puissance doit être soulevée B, afin de produire x?". Pour définir le logarithme, la base doit être un b nombre réel positif pas égal à 1 et x doit être un nombre positif.
Exemples
Par exemple, log 2 (16) = 4, depuis le 2 4 = 2 × 2 × 2 × 2 = 16. logarithmes peuvent aussi être négatif:
depuis
Un troisième exemple:. Log 10 (150) est d'environ 2.176, qui se situe entre 2 et 3, tout comme 150 se situe entre 10 100 et 2 = 10 3 = 1,000 Enfin, pour ne importe quelle base b, b log (b) = 1 et log b (1) = 0, puisque b 1 = b et b = 0 1, respectivement.
Identités logarithmiques
Plusieurs formules importantes, parfois appelés identités logarithmiques ou connectez lois, concernent logarithmes à l'autre.
Produit, du quotient, la puissance et la racine
Le logarithme d'un produit est la somme des logarithmes des nombres étant affecté; le logarithme du rapport de deux nombres est la différence des logarithmes. Le logarithme de la puissance p-ième d'un certain nombre de fois p est le logarithme du nombre lui-même; le logarithme d'une racine p ième d'est le logarithme du nombre divisé par p. Le tableau suivant répertorie ces identités avec des exemples:
| Formule | Exemple | |
|---|---|---|
| produit | 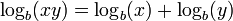 |  |
| quotient | 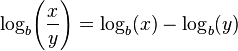 | 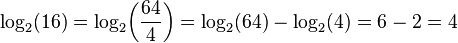 |
| puissance |  | 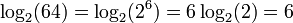 |
| racine | ![\ Log_b \ sqrt [p] {x} = \ frac {\ log_b (x)} p \,](../../images/2455/245579.png) |  |
Changement de base
Le logarithme log b (x) peut être calculée à partir des logarithmes de x et b par rapport à un k arbitraire de base en utilisant la formule suivante:
Typique calculatrices scientifiques de calculer les logarithmes aux bases 10 et e. Logarithmes à l'égard de ne importe quelle base b peuvent être déterminées en utilisant l'une de ces deux logarithmes par la formule précédente:
Étant donné un nombre x et son journal de logarithme b (x) à une base inconnue b, la base est donnée par:
Bases particulières
Parmi tous les choix de la base b, trois sont particulièrement fréquents. Ce sont b = 10, b = e (l' irrationnel constante mathématique ≈ 2,71828), et b = 2. Dans l'analyse mathématique , le logarithme en base e est très répandue en raison de ses propriétés analytiques particuliers expliqué ci-dessous. D'autre part, base 10 logarithmes sont faciles à utiliser dans les calculs manuels dans la décimale système de nombre:
Ainsi, log 10 (x) est en relation avec le nombre de chiffres décimaux des x un nombre entier positif: le nombre de chiffres est le plus petit entier strictement plus grande que log 10 (x). Par exemple, connectez-10 (1430) est d'environ 3,15. Le prochain nombre entier est 4, qui est le nombre de chiffres de 1430. Le logarithme en base deux est utilisée en informatique , où le système binaire est omniprésente.
Le tableau suivant répertorie notations communes pour logarithmes à ces bases et les domaines où ils sont utilisés. Beaucoup de disciplines écrivent log (x) au lieu de log b (x), lorsque la base prévue peut être déterminée à partir du contexte. Le journal notation b (x) produit également. Les «ISO notation" listes de colonnes désignations proposées par le Organisation internationale de normalisation ( ISO 31-11).
| Base de b | Nom log b (x) | Notation ISO | Autres notations | Utilisé dans |
|---|---|---|---|---|
| 2 | logarithme binaire | lb (x) | ld (x), log (x), lg (x) | informatique, théorie de l'information, les mathématiques |
| e | logarithme naturel | ln (x) | log (x) (En mathématiques et de nombreux langages de programmation ) | analyse mathématique, physique, chimie, statistiques , économie , et certains domaines de l'ingénierie |
| 10 | logarithme décimal | lg (x) | log (x) (Dans l'ingénierie, la biologie, l'astronomie), | divers ingénierie champs (voir Decibel voir ci-dessous), logarithme tables, ordinateur de poche calculatrices, spectroscopie |
Histoire
Prédécesseurs
Le Babyloniens dans le courant de 2000-1600 BC ont peut-être inventé le trimestre carré algorithme de multiplication pour multiplier deux nombres en utilisant seulement l'addition, la soustraction et une table de carrés. Toutefois, il ne pouvait pas être utilisé pour la division sans une table supplémentaire de inverses. Grandes tables de carrés trimestre ont été utilisés pour simplifier la multiplication des grands nombres exacts partir de 1817 jusqu'à ce que cela a été remplacée par l'utilisation des ordinateurs.
Michael Stifel publié Arithmetica Integra à Nuremberg en 1544, qui contient un tableau de nombres entiers et des puissances de 2 qui a été considéré comme une première version d'une table logarithmique.
Dans les 16e et début du 17e siècle un algorithme appelé prosthaphaeresis a été utilisée pour calculer la multiplication et la division. Ceci permet l'identité trigonométrique
ou similaire pour convertir les multiplications des ajouts et les recherches de table. Cependant logarithmes sont plus simples et nécessitent moins de travail. Il peut être montré en utilisant des nombres complexes que ce est essentiellement la même technique.
De Napier à Euler

La méthode des logarithmes a été publiquement mis en avant par John Napier en 1614, dans un livre intitulé Mirifici Logarithmorum Canonis Descriptio (Description de la règle merveilleux de logarithmes). Joost Bürgi inventé indépendamment logarithmes mais publié six ans après Napier.
Johannes Kepler , qui a utilisé les tables de logarithmes beaucoup de compiler son éphémérides et donc dédié à Napier, a fait remarquer:
... L'accent dans le calcul conduit Justus Byrgius [Joost Bürgi] sur le chemin de ces années très logarithmes nombre avant l'apparition du système de Napier; mais ... au lieu d'élever son enfant pour le bien public, il avait déserté dans la naissance.-Johannes Kepler, Tables rudolphines (1627)
Par soustractions répétées Napier calculée (1 - 10 -7) L L allant de 1 à 100. Le résultat pour L = 100 est d'environ 0,99999 = 1 - 10 -5. Napier calcule ensuite les produits de ces nombres avec 10 7 (1 - 10 -5) L L de 1 à 50, et a fait similaire à 0,9998 ≈ (1 - 10 -5) 20 0,995 ≈ 0,9 et 20. Ces calculs, qui occupaient 20 années, lui a permis de donner, pour un nombre N de 5 à 10 millions, le nombre L qui résout l'équation
Napier d'abord appelé L "un nombre artificiel", mais plus tard, a introduit le mot «logarithme» pour désigner un nombre qui indique un rapport: λόγος ( logos) proportion signifie, et ἀριθμός (arithmos) Numéro sens. En notation moderne, la relation à logarithmes naturels est:
où le rapprochement très proche correspond à l'observation que
L'invention a été rapidement et largement salué par la. Les travaux de Bonaventura Cavalieri (Italie), Edmund Wingate (France), Xue Fengzuo (Chine), et Johannes Kepler de CHILIAS logarithmorum (Allemagne) ont contribué à répandre le concept encore plus loin.

En 1647, Grégoire de Saint-Vincent logarithmes liée à la quadrature de l'hyperbole, en soulignant que la zone f (t) sous l'hyperbole de x = 1 à x = t satisfait
Le logarithme naturel a été décrite par Nicholas Mercator dans son travail Logarithmotechnia publié en 1668, bien que les professeur de mathématiques John Speidell avait déjà en 1619 compilé une table sur le logarithme naturel. Autour de 1730, Leonhard Euler défini la fonction exponentielle et le logarithme naturel
Euler a également montré que les deux fonctions sont inverses l'une de l'autre.
tables de logarithmes, règles à calcul et les applications historiques

En simplifiant les calculs difficiles, logarithmes contribué à l'avancement de la science, et surtout de l'astronomie . Ils ont critiqué aux progrès arpentage, navigation céleste, et d'autres domaines. Pierre-Simon Laplace appelés logarithmes
- "... [A] n artifice admirable qui, en réduisant à quelques jours le travail de plusieurs mois, double la durée de vie de l'astronome et lui épargne les erreurs et dégoût inséparables de longs calculs."
Un outil clé qui a permis l'utilisation pratique des logarithmes avant calculatrices et les ordinateurs était la table de logarithmes. Le premier tableau a été dressé par Henry Briggs en 1617, immédiatement après l'invention de Napier. Par la suite, des tables avec l'augmentation de la portée et la précision ont été écrits. Ces tableaux figurent les valeurs de log b (x) et b x pour tout nombre x dans une certaine gamme, à une certaine précision, pour une certaine base b (généralement b = 10). Par exemple, première table de Briggs contenait les logarithmes communs de tous les entiers dans la plage de 1 à 1000, avec une précision de 8 chiffres. Comme la fonction f (x) = x b est la fonction inverse de log b (x), il a été appelé l'antilogarithme. Le produit et le quotient de deux nombres c et d ont été systématiquement positifs correspondent à la somme et de la différence de leurs logarithmes. Le CD du produit ou le quotient c / d est venu de regarder le logarithme de la somme ou la différence, aussi par la même table:
et
Pour les calculs manuels qui exigent précision appréciable, qui effectuent les recherches des deux logarithmes, calcul de leur somme ou la différence, et en regardant le logarithme est beaucoup plus rapide que d'effectuer la multiplication par les méthodes antérieures telles que prosthaphaeresis, qui repose sur identités trigonométriques. Calculs des pouvoirs et racines sont réduits à des multiplications ou des divisions et look-ups par
et
Beaucoup de tables de logarithmes donnent logarithmes en fournissant séparément la caractéristique et mantisse de x, ce est-à-dire le la partie entière et la partie fractionnaire de log 10 (x). La caractéristique de 10 · x est un avantage de la caractéristique X, et leur mantisses sont les mêmes. Cela étend la portée de tables de logarithmes: étant donné un journal table de la liste 10 (x) pour tout entier x allant de 1 à 1000, le logarithme de 3542 est approchée par
Une autre application critique était la règle à calcul, une balance logarithmique divisées utilisées pour le calcul, comme illustré ici:
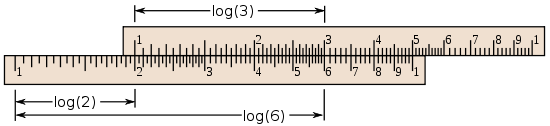
L'échelle logarithmique non coulissant, La règle de Gunter, a été inventé peu après l'invention de Napier. William Oughtred renforcée pour créer la diapositive règle-une paire de échelles logarithmiques mobiles par rapport à l'autre. Les nombres sont placés sur des échelles coulissantes à des distances proportionnelles aux différences entre leurs logarithmes. Coulissante l'échelle supérieure se élève de manière appropriée à l'ajout de mécanique logarithmes. Par exemple, en ajoutant la distance de 1 à 2 sur l'échelle inférieure à la distance de 1 à 3 sur l'échelle supérieure donne un produit de 6, qui est lue à la partie inférieure. La règle à calcul était un outil de calcul essentielle pour les ingénieurs et les scientifiques jusqu'à ce que les années 1970, car elle permet, au détriment de la précision, de calcul beaucoup plus rapide que les techniques basées sur les tables.
Propriétés analytiques
Une étude plus approfondie des logarithmes nécessite le concept d'une fonction . Une fonction est une règle qui, étant donné un numéro, produit un autre numéro. Un exemple est la production de la fonction x-ième puissance de b à partir de ne importe quel nombre réel x, où b est la base d'un nombre fixe. Cette fonction est écrit
Fonction logarithmique
Pour justifier la définition de logarithmes, il est nécessaire de montrer que l'équation
a une solution x et que cette solution est unique, à condition que y est positif et que b est positif et inégal à 1. Une preuve de ce fait nécessite la théorème de la valeur intermédiaire du primaire calcul . Ce théorème affirme qu'un fonction continue qui produit deux valeurs m et n donne également une valeur qui se situe entre m et n. Une fonction est continue si ce ne est pas "saut", qui est, si sa représentation graphique peut être établi sans soulever le stylet.
Cette propriété peut être montré à tenir pour la fonction f (x) = x b. Parce f prend arbitrairement grandes et petites arbitrairement des valeurs positives, ne importe quel nombre y> 0 est comprise entre f (x 0) et f (x 1) adapté pour x 0 et x 1. Par conséquent, le théorème de la valeur intermédiaire est garanti que l'équation f (x) = y a une solution. De plus, il n'y a qu'une solution de cette équation, parce que la fonction f est strictement croissante (pour b 1>), ou strictement décroissante (de 0 <b <1).
La solution unique x est le logarithme de y à la base b, b log (y). La fonction qui affecte à son logarithme y est appelée fonction logarithme ou une fonction logarithmique (ou juste logarithme).
Fonction inverse
La formule pour le logarithme d'une puissance indique en particulier que, pour tout nombre x,
En prose, en prenant la x-ième puissance de b, puis le base-b logarithme redonne x. Inversement, étant donné un nombre positif y, la formule
dit que la première prenant le logarithme et exponentielle puis redonne y. Ainsi, les deux possibilités de combinaison (ou composer ) logarithmes et exponentiation redonner le nombre original. Par conséquent, le logarithme de base b est la fonction inverse de f (x) = x b.
Fonctions inverses sont étroitement liés aux fonctions originales. Leur graphiques correspondent à l'autre lors de l'échange de la x - et les -coordinates de Y (ou à la réflexion sur la ligne diagonale x = y), comme indiqué à la droite: un point (t, u = b t) sur le graphique des rendements f un point (u, t = log b u) sur le graphique du logarithme et vice versa. En conséquence, connectez-b (x) diverge à l'infini (reçoit plus grand que ne importe quel nombre donné) si x tend vers l'infini, à condition que b est supérieur à un. Dans ce cas, connectez-b (x) est un fonction croissante. Pour b <1, log b (x) tend à moins l'infini à la place. Lorsque x tend vers zéro, connectez-b (x) va à moins l'infini pour b> 1 (plus l'infini pour b <1, respectivement).
Dérivée et primitive
Propriétés analytiques de fonctions passent à leurs inverses. Ainsi, en tant que f (x) = x b est une constante et fonction différentiable, est tellement journal b (y). En gros, une fonction continue est différentiable si son graphe n'a pas de "coins" pointus. En outre, comme le dérivé de f (x) est évaluée à ln (b) x b par les propriétés de la fonction exponentielle , la règle de la chaîne implique que la dérivée de log b (x) est donnée par
Autrement dit, le pente de la tangente toucher le graphique de la base-b logarithme au point (x, connectez-b (x)) est égale à 1 / (x ln (b)). En particulier, le dérivé de ln (x) est de 1 / x, ce qui implique que le primitive de 1 / x est ln (x) + C. Le dérivé avec un généralisée fonctionnelle argument de f (x) est
Le quotient au côté droit est appelé dérivée logarithmique de f. Informatique f '(x) au moyen de la dérivée de ln (f (x)) est connu comme différenciation logarithmique. La primitive de la ln logarithme naturel (x) est:
Formules connexes, comme primitives de logarithmes à d'autres bases peuvent être tirées de cette équation en utilisant le changement de bases.
Représentation intégrale du logarithme naturel
Le logarithme népérien de t accord avec la intégrante de 1 / dx x de 1 à t:
En d'autres termes, ln (t) est égale à la zone située entre l'axe x et le graphe de la fonction 1 / x allant de x = 1 pour x = t (figure de droite). Ceci est une conséquence du théorème fondamental du calcul et le fait que dérivé de ln (x) est de 1 / x. Le côté droit de cette équation peut servir de définition du logarithme naturel. formules de produit et de puissance logarithmiques peuvent être tirés de cette définition. Par exemple, la formule du produit ln (tu) = ln (t) + ln (u) on déduit que:
L'égalité (1) divise l'intégrale en deux parties, tandis que l'égalité (2) est un changement de variable (w = x / t). Dans l'illustration ci-dessous, la division correspond à diviser la zone dans les pièces jaunes et bleus. Redimensionner la zone bleue de la main gauche à la verticale par le facteur t et le rétrécissement par le même facteur horizontalement ne change pas sa taille. Déplacement de façon appropriée, la zone correspond à la courbe de la fonction f (x) = 1 / x fois. Par conséquent, la zone bleue de la main gauche, qui est l'intégrale de f (x) à partir de t tu est la même que l'intégrale de 1 à u. Cela justifie l'égalité (2) avec une preuve plus géométrique.
La formule de pouvoir ln (t r) r = ln (t) peut être obtenue d'une manière similaire:
La seconde utilise une égalité changement de variables ( l'intégration par substitution), w = x 1 / r.
La somme sur les inverses des nombres naturels,
est appelé le série harmonique. Elle est étroitement liée au logarithme naturel: quand n tend vers l'infini , la différence,
converge (ce est à dire, obtient arbitrairement proche) à un certain nombre connu sous le nom Constante d'Euler-Mascheroni. Ce aides de relation dans l'analyse de la performance des algorithmes tels que tri rapide.
Il existe également une autre représentation intégrale du logarithme qui est utile dans certaines situations.
Cela peut être vérifié en montrant qu'elle a la même valeur à x = 1 et le même dérivé.
Transcendance du logarithme
Le logarithme est un exemple d'un fonction transcendantale et d'un point de vue théorique, le Gelfond-Schneider théorème affirme que logarithmes prennent généralement des valeurs «difficiles». La déclaration officielle se appuie sur la notion de nombres algébriques, qui comprend tous les nombres rationnels , mais aussi des valeurs telles que la racine carrée de 2 ou
Les nombres complexes qui ne sont pas algébriques sont appelés transcendantale; par exemple, π et e sont ces numéros. Presque tous les nombres complexes sont transcendantale. L'utilisation de ces notions, le théorème États Gelfond-Scheider qu'étant donné deux nombres algébriques a et b, connectez-vous b (a) est soit un nombre transcendant ou un nombre rationnel p / q (auquel cas un q = b p, donc a et b étaient étroitement liées pour commencer).
Calcul
Logarithmes sont faciles à calculer, dans certains cas, comme log 10 (1000) = 3. En général, les logarithmes peuvent être calculées en utilisant la série de puissance ou de la arithmétique moyenne géométrique, ou être extraites d'un précalculée table de logarithme qui fournit une précision fixe. la méthode de Newton , une méthode itérative pour la résolution d'équations environ, peut également être utilisé pour calculer le logarithme, parce que sa fonction inverse de la fonction exponentielle, peut être calculée de manière efficace. Utilisation de tables de consultation, CORDIC méthodes analogues peuvent être utilisées pour calculer les logarithmes si les seules opérations disponibles sont ajout et décalages de bits. En outre, le algorithme de logarithme binaire calcule lb (x) de façon récursive en fonction des élévations au carré répétées de x, en tirant parti de la relation
série Power
- Série de Taylor
Pour tout nombre réel z qui satisfait 0 <z <2, la formule suivante est vérifiée:
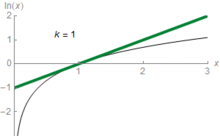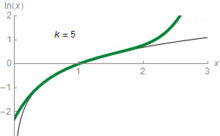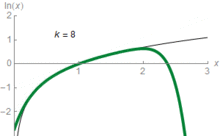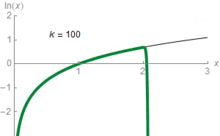
Ce est un raccourci pour dire que ln (z) peut être approchée à une valeur de plus en plus précise par les expressions suivantes:
Par exemple, avec z = 1,5 on obtient la troisième approximation 0,4167, qui est d'environ 0,011 supérieure à ln (1,5) = 0,405465. Cette série se rapproche de ln (z) avec une précision arbitraire, à condition que le nombre de termes de la somme est assez grand. Dans le calcul élémentaire, ln (z) est donc la limite de cette série. Ce est la série de Taylor du logarithme naturel à z = 1 La série de Taylor de ln z fournit une approximation utile en particulier pour ln (1 + z) où z est petit, |. z | << 1, depuis lors,
Par exemple, avec z = 0,1 l'approximation de premier ordre donne ln (1,1) ≈ 0,1, ce qui est inférieur à 5% sur la valeur correcte 0,0953.
- Série plus efficace
Une autre série est basé sur la zone fonction tangente hyperbolique:
pour tout nombre réel z> 0. Utilisation de la Sigma notation, ce est aussi écrit que
Cette série peut être dérivé de la série de Taylor ci-dessus. Elle converge plus rapidement que la série de Taylor, en particulier si z est proche de 1. Par exemple, pour z = 1,5, les trois premiers termes de la deuxième ln approximatif de série (1.5) avec une erreur d'environ 3 × 10 -6. La convergence rapide pour z proche de 1 peut être mis à profit de la manière suivante: étant donné un ln faible précision rapprochement y ≈ (z) et la mise
le logarithme de z est:
Le meilleur de la première approximation y est, plus A est à 1, de sorte que son logarithme peut être calculé de manière efficace. A peut être calculé en utilisant la série exponentielle , qui converge rapidement fourni y ne est pas trop grand. Le calcul du logarithme de la plus grande z peut être réduit à de plus petites valeurs de z en écrivant z = a · 10 b, de sorte que ln (z) = ln (a) + b · ln (10).
Procédé étroitement liée peut être utilisé pour calculer le logarithme de nombres entiers. De la série ci-dessus, il se ensuit que:
Si le logarithme d'un grand entier n est connue, cette série donne une série convergente rapide pour log (n + 1).
Rapprochement moyenne arithmétique-géométrique
Le rendements moyens arithmétiques-géométriques approximations de haute précision du logarithme naturel. ln (x) est approchée avec une précision de 2 - p (ou p bits de précision) par la formule suivante (en raison de Carl Friedrich Gauss ):
Ici, M représente la moyenne arithmétique-géométrique. Il est obtenu en calculant de manière répétée le moyen ( moyenne arithmétique ) et la racine carrée du produit de deux nombres ( moyenne géométrique). De plus, m est choisi de telle sorte que
Tant le moyen arithmétique-géométrique et les constantes π et ln (2) peut être calculé avec convergeant rapidement série.
Applications
Logarithmes ont de nombreuses applications à l'intérieur et en dehors de mathématiques. Certains de ces événements sont liés à la notion de invariance d'échelle. Par exemple, chaque chambre de l'enveloppe d'un Nautilus est une copie approximative de la suivante, réduite par un facteur constant. Cela donne lieu à une spirale logarithmique. La loi de Benford sur la distribution des premiers chiffres peut également se expliquer par l'invariance d'échelle. Logarithmes sont également liés à auto-similarité. Par exemple, logarithmes apparaissent dans l'analyse d'algorithmes qui permettent de résoudre un problème en le divisant en deux petits problèmes similaires et de correction de leurs solutions. Les dimensions de formes géométriques auto-similaires, ce est-formes dont les parties ressembler à l'image globale sont également basés sur les logarithmes. Les échelles logarithmiques sont utiles pour quantifier la variation relative d'une valeur par opposition à sa différence absolue. En outre, parce que le journal de la fonction logarithmique (x) croît très lentement pour les grandes x, échelles logarithmiques sont utilisés pour compresser les données scientifiques de grande envergure. Logarithmes se produisent également dans de nombreuses formules scientifiques, tels que le Équation de Tsiolkovski, le Équation Fenske, ou la Équation de Nernst.
Échelle logarithmique
Des quantités scientifiques sont souvent exprimés en logarithmes d'autres grandeurs, en utilisant une échelle logarithmique. Par exemple, le décibel est une unité de mesure logarithmique. Il est basé sur le logarithme décimal de ratios - 10 fois le logarithme décimal d'un rapport de puissance ou 20 fois le logarithme décimal d'un rapport de tension. Il est utilisé pour quantifier la perte de niveaux de tension en des signaux électriques d'émission, pour décrire les niveaux de bruits électriques dans acoustique, et les absorbance de la lumière dans les domaines de spectrométrie et optiques . Le rapport signal sur bruit décrivant la quantité de indésirables bruit par rapport à un (significatif) signal est également mesuré en décibels. Dans la même veine, le Peak Signal to Noise Ratio est couramment utilisé pour évaluer la qualité du son et de méthodes de compression d'image en utilisant le logarithme.
La force d'un tremblement de terre est mesurée en prenant le logarithme décimal de l'énergie émise au tremblement de terre. Il est utilisé dans le échelle de magnitude de moment ou de la Échelle de Richter. Par exemple, un séisme de 5,0 libère 10 fois et 6,0 libère 100 fois l'énergie d'un 4.0. Un autre échelle logarithmique est magnitude apparente. Il mesure la brillance des étoiles logarithmique. Encore un autre exemple est pH en chimie ; Le pH est le logarithme négatif de la commune de activité de ions hydronium (la forme hydrogène ions H + prennent dans l'eau). L'activité des ions hydronium dans l'eau neutre est de 10 -7 mol.L -1, d'où un pH de 7. Le vinaigre a typiquement un pH d'environ 3. La différence de 4 correspond à un rapport de 4 10 de l'activité, ce est l'activité des ions hydronium de vinaigre est d'environ 10 -3 mol · L -1.
(Log-linéaires) semilog graphiques utilisent le concept d'échelle logarithmique pour la visualisation: un axe, généralement l'une verticale, est échelle logarithmique. Par exemple, le graphique à droite comprime la forte augmentation 1-1000000 million au même espace (sur l'axe vertical) que l'augmentation du 1 au 1 million. Dans ces graphiques, fonctions exponentielles de la forme f ( x ) = a · b X apparaissent en lignes droites avec pente égale au logarithme de b . Log-Log graphiques échelle logarithmique deux axes, ce qui provoque fonctions de la forme f ( x ) = un · x k soient dépeints comme des lignes droites avec une pente égale à l'exposant k . Cette méthode est appliquée dans la visualisation et l'analyse des lois de puissance.
Psychologie
Logarithmes se produisent dans plusieurs lois décrivant la perception humaine: . la loi de Hick propose une relation logarithmique entre le moment où les individus prennent pour choisir une alternative et le nombre de choix qu'ils ont la loi de Fitts prédit que le temps nécessaire pour se déplacer rapidement vers une zone cible est une fonction logarithmique de la distance et de la taille de la cible. En psychophysique, la loi de Weber-Fechner propose une relation logarithmique entre stimulus et la sensation comme la réelle contre le poids perçu d'un article une personne est porteur. (Cette «loi», cependant, est moins précise que les modèles plus récents, comme la loi de puissance de Stevens.)
Des études psychologiques ont trouvé que les individus ont tendance mathématiquement peu sophistiqués pour estimer les quantités logarithmique, ce qui signifie qu'ils positionnent un numéro sur une ligne banalisée selon son logarithme, de sorte que 10 se positionne comme près de 20 100 est à 200. L'augmentation de la compréhension mathématique décale cela une estimation linéaire (positionnement 100 10x plus loin).
La théorie des probabilités et des statistiques
Logarithmes se posent dans la théorie des probabilités : la loi des grands nombres dicte que, pour une pièce de monnaie, comme le nombre de pièces de monnaie-lancers augmente à l'infini, la proportion observée des chefs approche de la moitié . Les fluctuations de cette proportion d'environ un demi-sont décrits par la loi du logarithme itéré.
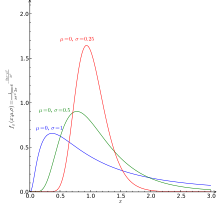
Logarithmes se produisent également dans les distributions log-normale. Lorsque le logarithme d'une variable aléatoire a une distribution normale , la variable est dit avoir une distribution log-normale. Distributions log-normale sont rencontrées dans de nombreux domaines, où une variable est formé comme le produit de nombreuses variables aléatoires positives indépendants, par exemple dans l'étude de la turbulence.
Logarithmes sont utilisés pour l'estimation du maximum de vraisemblance des paramétriques des modèles statistiques. Pour un tel modèle, la fonction de vraisemblance dépend d'au moins un paramètre qui doit être estimée. Un maximum de la fonction de vraisemblance se produit au même paramètre-valeur en tant que maximum du logarithme de la probabilité (la « de vraisemblance logarithmique »), parce que le logarithme est une fonction croissante. La log-vraisemblance est plus facile de maximiser, en particulier pour les probabilités multipliées pour des variables aléatoires indépendantes.
La loi de Benford décrit l'apparition de chiffres dans de nombreux ensembles de données, telles que la hauteur des bâtiments. Selon la loi de Benford, la probabilité que la première décimale chiffres d'un élément dans l'échantillon de données est d (1-9) est égale à log 10 ( d + 1) - log 10 ( d ), indépendamment de l'unité de mesure. Ainsi, environ 30% des données peut être attendu d'avoir 1 comme premier chiffre, 18% début avec 2, etc. comptes examinent écarts par rapport à la loi de Benford pour détecter comptabilité frauduleuse.
La complexité du calcul
Analyse des algorithmes est une branche de la science informatique qui étudie la performance des algorithmes (des programmes informatiques de résoudre un certain problème). Logarithmes sont utiles pour décrire des algorithmes qui divisent un problème en plus petits, et rejoignent les solutions des sous-problèmes.
Par exemple, pour trouver un numéro dans une liste triée, l' algorithme de recherche binaire vérifie l'entrée du milieu et procède à la moitié avant ou après l'entrée du milieu, si le nombre est toujours pas trouvé. Cet algorithme nécessite, en moyenne, log 2 ( N ), des comparaisons où N est la longueur de la liste. De même, la fusionner algorithme de tri trie une liste non triés en divisant la liste en deux moitiés et trier ces premiers avant de fusionner les résultats. Fusionner algorithmes de tri nécessitent généralement un temps approximativement proportionnelle à N · log ( N ) . La base du logarithme est pas spécifié ici, car le résultat ne change que d'un facteur constant lorsque l'autre base est utilisée. Un facteur constant, est généralement négligée dans l'analyse des algorithmes sous l'étendard modèle de coût uniforme.
Une fonction f ( x ) est dite à croître de façon logarithmique si f ( x ) est (exactement ou approximativement) proportionnelle au logarithme de x . (Descriptions biologiques de croissance de l'organisme, cependant, utilisent ce terme pour une fonction exponentielle.) Par exemple, tout nombre naturel N peut être représentée sous forme binaire dans pas plus de journal 2 ( N ) + 1 bits. En d'autres termes, la quantité de mémoire nécessaire pour stocker N pousse logarithmique avec N .
Entropie et le chaos
L'entropie est une mesure générale de la maladie d'un système. En thermodynamique statistique , l'entropie S de quelque système physique est défini comme
La somme est supérieure à tous les états possibles i du système en question, tel que les positions des particules de gaz dans un récipient. Par ailleurs, p je est la probabilité que l'état i est atteint et k est la constante de Boltzmann. De même, entropie en théorie de l'information mesure la quantité d'informations. Si un destinataire du message peut s'attendre à une quelconque des N messages possibles avec une probabilité égale, la quantité d'information transmise par l'un quelconque tel message est quantifiée comme log 2 ( N ) bits.
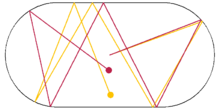
Exposants de Lyapunov utilisent logarithmes afin d'évaluer le degré de chaoticité d'un système dynamique. Par exemple, pour une particule se déplaçant sur une table de billard de forme ovale, même de petits changements des conditions initiales conduisent à des trajectoires très différentes de la particule. De tels systèmes sont chaotique dans une façon déterministe, parce que les petites erreurs de mesure de l'état initial mènent largement prévisible aux différents états finaux. Au moins un exposant de Lyapunov d'un système déterministe chaotique est positif.
Fractales
Logarithmes se produisent dans les définitions de la dimension de fractales . Les fractales sont des objets géométriques qui sont auto-similaire: petites pièces reproduisent, au moins grossièrement, l'ensemble de la structure globale. Le triangle de Sierpinski (photo) peut être couvert par trois copies de lui-même, chacun ayant des côtés la moitié de la longueur d'origine. Cela rend la dimension de Hausdorff de cette structure log (3) / log (2) ≈ 1,58 . Une autre notion basée logarithme-de dimension est obtenue en comptant le nombre de boîtes nécessaires pour couvrir la fractale en question.
Musique
Logarithmes sont liés à des tons et musicales intervalles. En tempérament égal, le rapport de fréquence ne dépend que de l'intervalle entre deux tons, pas sur la fréquence spécifique, ou pas, des tons différents. Par exemple, le noter A a une fréquence de 440 Hz et B-plat a une fréquence de 466 Hz. L'intervalle entre A et B-flat est un demi-ton, tout comme celui entre bémol et B (fréquence 493 Hz). En conséquence, les ratios de fréquence d'accord:
Par conséquent, les logarithmes peuvent être utilisés pour décrire les intervalles: un intervalle est mesurée en demi-tons en prenant la base 2 1/12 logarithme du rapport des fréquences, alors que la base 2 1/1200 logarithme du rapport de fréquence exprime l'intervalle en cents, centièmes de demi-ton. Ce dernier est utilisé pour le codage plus fin, comme il est nécessaire pour les tempéraments non égaux.
| Intervalle (Les deux sonorités sont reproduites en même temps) | Jeu de tonalité 1/12 | Jeu Semitone | Tierce majeure jeu | Troisième jeu Major | jeu de Tritone | jeu de Octave |
| Fréquence rapport r |  |  | 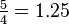 | ![\begin{align} 2^{\frac 4 {12}} & = \sqrt[3] 2 \\ & \approx 1.2599 \end{align}](../../images/2457/245704.png) |  | 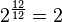 |
Correspondant nombre de demi-tons ![\log_{\sqrt[12] 2}(r) = 12 \log_2 (r)](../../images/2457/245707.png) |  | 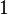 |  | 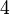 |  | 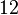 |
Correspondant nombre de cents ![\log_{\sqrt[1200] 2}(r) = 1200 \log_2 (r)](../../images/2457/245712.png) | 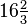 |  |  |  | 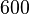 |  |
La théorie des nombres
Logarithmes naturels sont étroitement liés au comptage des nombres premiers (2, 3, 5, 7, 11, ...), un sujet important dans la théorie des nombres . Pour tout entier x , la quantité de nombres premiers inférieurs ou égaux à x est notée π ( x ). Le théorème des nombres premiers affirme que π ( x ) est approximativement donnée par
en ce sens que le rapport de π ( x ) et en ce que lorsque une fraction approches x tend vers l'infini. Par conséquent, la probabilité qu'un nombre choisi au hasard entre 1 et x est un nombre premier est inversement proportionnel au nombre de chiffres décimaux de x . Une bien meilleure estimation de π ( x ) est donnée par la fonction intégrale logarithmique compensé Li ( x ), défini par
Le Hypothèse de Riemann, un des plus anciens mathématiques ouvertesconjectures, peut être déclaré en termes de comparaison π (x) et Li (x). Le Erdős-Kac théorème décrivant le nombre de distinctesfacteurs premiers implique également le logarithme naturel.
Le logarithme de n factorielle , n ! = 1 · 2 · ... · n , est donnée par
Ceci peut être utilisé pour obtenir la formule de Stirling, une approximation de n ! pour les grands n .
Généralisations
Logarithme complexe
Lesnombres complexes d'unerésolution de l'équation
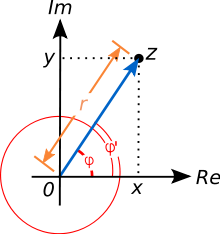
sont appelés logarithmes complexes . Ici, z est un nombre complexe. Un nombre complexe est souvent représenté comme z = x + iy , où x et y sont des nombres réels et i est l' unité imaginaire . Un tel nombre peut être visualisé par un point dans le plan complexe , comme le montre à droite. La forme polaire code pour un non-zéro nombre complexe z par sa valeur absolue , soit la distance r à l' origine, et un angle entre le x axe et la droite passant par l'origine et z . Cet angle est appelé l' argument de la z . La valeur absolue r de z est
L'argument est pas spécifié uniquement par z : à la fois φ et φ '= φ + 2π sont arguments de z parce que l'ajout 2π radians ou 360 degrés pour φ correspond à "enroulement" autour de l'origine contre-horaire par un tourner. nombre complexe La résultante est à nouveau z , comme illustré à droite. Cependant, les satisfait de exactement un argument -π <φ et φ ≤ π . Il est appelé le principal argument , noté Arg ( z ), avec un capital A . (Une alternative est la normalisation 0 ≤ Arg ( z ) <2π .)
En utilisantdes fonctions trigonométriques sinus etcosinus, ou lecomplexe exponentielle, respectivement,ret φ sont telles que les identités suivantes sont vérifiées:
Cela implique que l'une-ièmepuissance deeest égale àz, où
φ est l'argument principal Arg ( z ) et n est un entier arbitraire. Tout un est appelé un logarithme complexe de z . Il existe une infinité d'entre eux, à la différence du logarithme réel définie de manière unique. Si n = 0 , une est appelée la valeur principale du logarithme, notée Connexion ( z ). L'argument principal de tout nombre réel positif x est 0; donc Log ( x ) est un nombre réel et est égal au logarithme réel (naturel). Cependant, les formules ci-dessus pour les logarithmes de produits et les pouvoirs ne pas généraliser à la valeur principale du logarithme complexe.
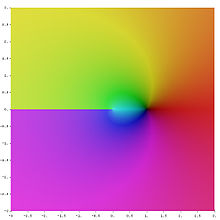
L'illustration ci-contre représente Connexion ( z ). La discontinuité, qui est, le saut dans la teinte à la partie négative du x - ou axe réel, est causée par le saut de l'argument principal il. Ce lieu est appelé une branche coupée. Ce comportement ne peut être contournée en laissant tomber la restriction de gamme sur φ. Ensuite, l'argument de z et, par conséquent, son logarithme devenir fonctions à valeurs multiples.
Inverses des autres fonctions exponentielles
Exponentiation se produit dans de nombreux domaines des mathématiques et sa fonction inverse est souvent désigné comme le logarithme. Par exemple, le logarithme d'une matrice est la fonction inverse (à valeurs multiples) de la matrice exponentielle. Un autre exemple est le p -adique logarithme, la fonction inverse de la p -adique exponentielle. Les deux sont définis par série de Taylor analogue au cas réel. Dans le contexte de la géométrie différentielle , la carte exponentielle mappe l' espace tangent à un point d'un collecteur à un voisinage de ce point. Son inverse est aussi appelé le (ou log) carte logarithmique.
Dans le contexte de groupes finis exponentiation est donnée en multipliant plusieurs reprises un élément du groupebavec lui-même. Le logarithme discret est l'entiernde résoudre l'équation
où x est un élément du groupe. Réaliser l'exponentiation peut être fait efficacement, mais le logarithme discret est censé être très difficile à calculer dans certains groupes. Cette asymétrie a d'importantes applications dans la cryptographie à clé publique, comme par exemple dans l' échange de clés Diffie-Hellman, une routine qui permet de sécuriser les échanges de chiffrement des clés sur des canaux d'information non garantis. Le logarithme de Zech est liée à la logarithme discret dans le groupe multiplicatif des non -Zero éléments d'une champ fini.
Autres fonctions inverses logarithme comme incluent le logarithme à double ln (ln ( x )), le -logarithme hyper-4 super ou (une légère variation de ce qui est appelé logarithme itéré en informatique), la fonction W de Lambert, et le logit . Ils sont les fonctions inverses de la double fonction exponentielle, tétration, de f ( w ) = nous w , et de la fonction logistique, respectivement.
Concepts associés
Du point de vue mathématiques pures, l'identité journal ( cd ) = log ( c ) + log ( d ) exprime un isomorphisme de groupe entre positifs réels en vertu de la multiplication et de reals sous addition. Fonctions logarithmiques sont les seuls isomorphismes continues entre ces groupes. Au moyen de ce isomorphisme, la mesure de Haar ( mesure de Lebesgue) dx sur les réels correspond à la mesure de Haar dx / x sur les réels positifs. En analyse et complexes la géométrie algébrique, différentiels formes de la forme df / f sont connus comme des formes avec logarithmique pôles.
Le polylogarithme est la fonction définie par
Elle est en relation avec le logarithme naturel en Li 1 ( z ) = -ln (1 - z ) . En outre, Li s (1) est égale à la fonction de Riemann zêta ζ ( s ).
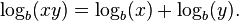
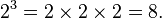

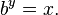
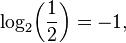





![\ Cos \, \ alpha \, \ cos \, \ beta = \ frac12 [\ cos (\ alpha + \ beta) + \ cos (\ alpha \ bêta)]](../../images/2455/245585.png)
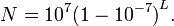
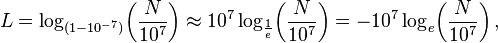
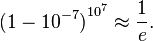
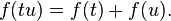

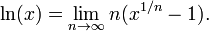



![\ Sqrt [d] {c} = c ^ {\ frac 1 d} = b ^ {\ frac {1} {d} \ log_b (c)}. \,](../../images/2456/245605.png)
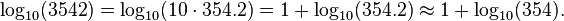
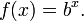
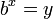


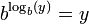

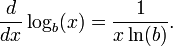



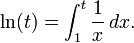


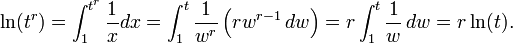
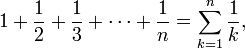
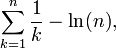
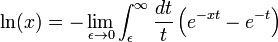
![\ Sqrt {-5+ \ sqrt [3] {3/13}}.](../../images/2456/245647.png)



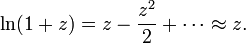
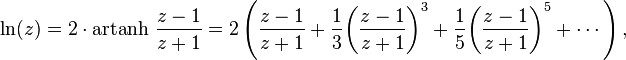
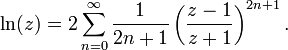


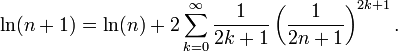





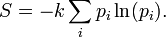



![\frac{466}{440} \approx \frac{493}{466} \approx 1.059 \approx \sqrt[12]2.](../../images/2457/245700.png)