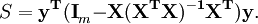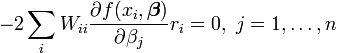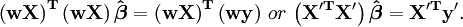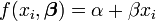Moindres carrés
Contexte des écoles Wikipédia
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Voir http://www.soschildren.org/sponsor-a-child pour connaître le parrainage d'enfants.
La méthode des moindres carrés, aussi connu comme l'analyse de régression , est utilisé pour modéliser des données numériques obtenues à partir d'observations en ajustant les paramètres d'un modèle de façon à obtenir un ajustement optimal des données. Le meilleur ajustement est caractérisé par la somme des carrés des résidus ont moins de sa valeur, un étant résiduelle la différence entre la valeur observée et la valeur donnée par le modèle. La méthode a été décrite par Carl Friedrich Gauss autour de 1794. moindres carrés correspond à la critère du maximum de vraisemblance, si les erreurs expérimentales ont une distribution normale . L'analyse de régression est disponible dans la plupart progiciels statistiques.
Histoire
Contexte
La méthode des moindres carrés a grandi dans les champs de l'astronomie et de géodésie que des scientifiques et mathématiciens a cherché à apporter des solutions aux défis de naviguer les océans de la Terre au cours de l' âge de l'exploration . La description précise du comportement des corps célestes était essentielle pour permettre aux navires de naviguer en haute mer où, avant marins devaient se appuyer sur des observations terrestres pour déterminer les positions de leurs navires.
La méthode a été le point culminant de plusieurs avancées qui ont eu lieu au cours de la dix-huitième siècle :
- La combinaison de différentes observations prises dans les mêmes conditions plutôt que de simplement essayer de son mieux pour observer et enregistrer une seule observation précise. Cette approche a notamment été utilisé par Tobias Mayer en étudiant la libration de la Lune.
- La combinaison de différentes observations comme étant la meilleure estimation de la valeur réelle; erreurs diminuent avec l'agrégation plutôt que augmentation, peut-être d'abord exprimée par Roger Cotes.
- La combinaison de différentes observations prises dans des conditions différentes que notamment effectuée par Roger Joseph Boscovich dans son travail sur la forme de la terre et Pierre-Simon Laplace dans son travail pour expliquer les différences dans le mouvement de Jupiter et de Saturne .
- Le développement d'un critère qui peut être évaluée pour déterminer quand la solution avec l'erreur minimum a été atteint, développée par Laplace dans sa Procédé de situation.
Le procédé lui-même
Carl Friedrich Gauss est crédité de développer les fondements de la base de l'analyse des moindres carrés en 1795 à l'âge de dix-huit ans.
Une première démonstration de la force de la méthode de Gauss est venue quand il a été utilisé pour prédire le futur emplacement de l'astéroïde nouvellement découvert Ceres . Sur Le 1er janvier 1801 , l'astronome italien Giuseppe Piazzi découvre Cérès et était en mesure de suivre son chemin pendant 40 jours avant qu'il a été perdu dans l'éclat du soleil. Sur la base de ces données, on a voulu déterminer l'emplacement de Cérès après qu'il a émergé de derrière le soleil sans résoudre le compliquée équations non linéaires de Kepler de mouvement planétaire. Les seules prévisions qui ont permis avec succès astronome hongrois Franz Xaver von Zach de déménager Ceres étaient celles effectuées par le 24-year-old Gauss en utilisant l'analyse des moindres carrés.
Gauss n'a pas publié la méthode jusqu'à 1809 , quand il est apparu dans le volume deux de son travail sur la mécanique céleste, Theoria Motus Corporum Coelestium dans sectionibus conicis solem ambientium. En 1829 , Gauss a été en mesure d'affirmer que l'approche des moindres carrés à l'analyse de régression est optimal dans le sens que, dans un modèle linéaire où les erreurs ont une moyenne de zéro, ne sont pas corrélées, et ont des variances égales, les meilleurs estimateurs linéaires sans biais de les coefficients sont les estimateurs des moindres carrés. Ce résultat est connu comme le Théorème de Gauss-Markov.
L'idée de moindres carrés analyse a également été formulé de façon indépendante par le Français Adrien-Marie Legendre en 1805 et de l'American Robert Adrain en 1808 .
Énoncé du problème
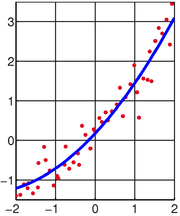
L'objectif consiste à ajuster les paramètres d'une fonction de modèle de manière à se adapter mieux à un ensemble de données. Un ensemble de données simple consiste à m points (paires de données) 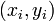 , I = 1, ..., m, où
, I = 1, ..., m, où  est un variable indépendante et
est un variable indépendante et  est un variable dépendante dont la valeur est trouvée par l'observation. La fonction de modèle a la forme
est un variable dépendante dont la valeur est trouvée par l'observation. La fonction de modèle a la forme  , Où les paramètres réglables n ont lieu dans le vecteur
, Où les paramètres réglables n ont lieu dans le vecteur  . Nous voulons trouver les valeurs des paramètres pour lesquels le «meilleur» modèle correspond aux données. La méthode des moindres carrés définit «meilleur» que lorsque la somme, S, des carrés des résidus
. Nous voulons trouver les valeurs des paramètres pour lesquels le «meilleur» modèle correspond aux données. La méthode des moindres carrés définit «meilleur» que lorsque la somme, S, des carrés des résidus
est un minimum. Un résiduelle est définie comme la différence entre les valeurs de la variable dépendante et le modèle.
Un exemple d'un modèle est celui de la ligne droite. En notant que l'interception  et comme la pente
et comme la pente  , La fonction modèle est donnée par
, La fonction modèle est donnée par
Voir linéaire des moindres carrés # Exemple pour un exemple entièrement travaillé sur ce modèle.
Un point de données peut comporter plus d'une variable indépendante. Par exemple, lors du montage d'un avion à un ensemble de mesures de hauteur, le plan est une fonction de deux variables indépendantes, x et z, par exemple. Dans le cas le plus général, il peut y avoir une ou plusieurs variables indépendantes et une ou plusieurs variables dépendantes à chaque point de données.
Résoudre le problème des moindres carrés
Problèmes de moindres carrés se répartissent en deux catégories, linéaire et non-linéaire. Le problème linéaires des moindres carrés a une solution de forme fermée, mais le problème non linéaire doit être résolu par raffinement itératif; à chaque itération du système est approchée par une linéaire, de sorte que le calcul de base est similaire dans les deux cas.
Le minimum de la somme des carrés est obtenu par réglage de la gradient à zéro. Depuis le modèle contient n paramètres il ya n équations gradient.
et que  les équations deviennent de gradient
les équations deviennent de gradient
Les équations de gradient se appliquent à tous les problèmes des moindres carrés. Chaque problème particulier nécessite expressions particulières pour le modèle et ses dérivées partielles.
Linéaire des moindres carrés
Le système est linéaire quand le modèle comprend un combinaison linéaire des paramètres.
Les coefficients  sont des constantes ou des fonctions de la variable indépendante, x i.
sont des constantes ou des fonctions de la variable indépendante, x i.
Depuis 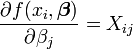 et
et 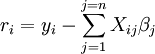 les équations deviennent de gradient
les équations deviennent de gradient
qui, réarrangement, devenu n équations linéaires simultanées, les équations normales.
Les équations normales sont écrites en notation matricielle
Solution des équations normales donne les estimateurs des moindres carrés, 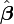 , Des valeurs de paramètre. Voir moindres carrés linéaires (exemple) et la régression linéaire (par exemple) pour des exemples numériques élaborée.
, Des valeurs de paramètre. Voir moindres carrés linéaires (exemple) et la régression linéaire (par exemple) pour des exemples numériques élaborée.
Moindres carrés non linéaires
Il n'y a pas de solution à un problème de fermeture moins carrés non linéaire. Au lieu de cela, les valeurs initiales doivent être choisies pour les paramètres. Ensuite, les paramètres sont raffinées de façon itérative, à savoir les valeurs sont obtenues par approximations successives.
k est un nombre d'itérations et le vecteur d'incréments,  qui est connu comme le vecteur de décalage. A chaque itération Le modèle peut être linéarisé par approximation d'un premier ordre série de Taylor à propos de l'expansion
qui est connu comme le vecteur de décalage. A chaque itération Le modèle peut être linéarisé par approximation d'un premier ordre série de Taylor à propos de l'expansion 
Le Jacobien, J est une fonction de constantes, la variable indépendante et les paramètres, de sorte qu'il passe d'une itération à l'autre. Les résidus sont donnés par
et les équations deviennent de gradient
qui, réarrangement, devenu n équations linéaires simultanées, les équations normales.
Les équations normales sont écrites en notation matricielle
Ce sont les équations définissant de la Algorithme de Gauss-Newton.
Les différences entre linéaire et non-linéaire des moindres carrés
- La fonction modèle f, dans LLSQ (linéaire des moindres carrés) est une combinaison linéaire des paramètres de la forme
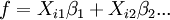 Le modèle peut représenter une ligne droite, une parabole ou toute autre fonction de type polynomiale. Dans NLLSQ (non-linéaire des moindres carrés) les paramètres apparaissent comme des fonctions, telles que
Le modèle peut représenter une ligne droite, une parabole ou toute autre fonction de type polynomiale. Dans NLLSQ (non-linéaire des moindres carrés) les paramètres apparaissent comme des fonctions, telles que  et ainsi de suite. Si les dérivés
et ainsi de suite. Si les dérivés 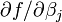 sont soit constante ou ne dépendent que des valeurs de la variable indépendante, le modèle est linéaire dans les paramètres. Sinon, le modèle est non linéaire.
sont soit constante ou ne dépendent que des valeurs de la variable indépendante, le modèle est linéaire dans les paramètres. Sinon, le modèle est non linéaire. - NLLSQ nécessite valeurs initiales pour les paramètres, LLSQ ne fait pas.
- NLLSQ exige que le jacobien être calculée. Des expressions analytiques pour les dérivées partielles peuvent être compliquées. Si expressions analytiques sont impossibles à obtenir les dérivées partielles doivent être calculés par approximation numérique.
- Dans NLLSQ divergence est un phénomène commun alors que dans LLSQ il est assez rare. La divergence se produit lorsque la somme des carrés augmente d'une itération à l'autre. Elle est causée par l'insuffisance de l'approximation que la série de Taylor peut être tronqué à la première période. Lorsque divergence se produit la méthode doit être modifiée. Le Algorithme de Levenberg-Marquardt offre une bonne protection contre la divergence en tournant le vecteur de changement dans la direction de la plus grande pente. Par la convergence de définition est assurée lorsque les points de vecteur de changement dans la direction de la plus grande pente.
- NLLSQ est un processus itératif processus.Les intrinsèquement itératif doit être terminé quand un critère de convergence est satisfaite. LLSQ solutions peuvent être calculés en utilisant des procédés directs, bien que des problèmes avec un grand nombre de paramètres sont habituellement résolus par des méthodes itératives, comme le Méthode de Gauss-Seidel ..
- Dans LLSQ la solution est unique, mais dans NLLSQ il peut y avoir plusieurs minima dans la somme des carrés.
- Dans NLLSQ estimations des erreurs de paramètres sont biaisée, mais dans LLSQ ils ne sont pas.
Ces différences doivent être considérés chaque fois que la solution d'un problème des moindres carrés non linéaire est recherché.
Moindres carrés, analyse de régression et statistiques
Les méthodes de moindres carrés et analyse de régression peuvent sembler être des méthodes différentes, mais il ya des similitudes importantes entre ceux qui sont obscurcies par l'utilisation de différentes langues utilisées pour décrire les méthodes. Les deux méthodes sont utilisées pour modéliser les données obtenues à partir d'observations, et les deux peuvent utiliser les mêmes techniques numériques.
Dans les sciences physiques le modèle a généralement une base théorique. Par exemple, un ressort devrait obéir La loi de Hooke, qui indique que l'extension d'un ressort est proportionnelle à la force F, qui lui est appliquée.
constitue le modèle, où F est la variable indépendante. Pour déterminer la force constante, k, une série de mesures avec différentes forces produira un ensemble de données, 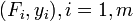 , Où y i est une extension de printemps mesurée. La somme des carrés à minimiser est
, Où y i est une extension de printemps mesurée. La somme des carrés à minimiser est
L'estimation des moindres carrés de la force constante, k, est donnée par
Ici, il est supposé que l'application de la force provoque le ressort à étendre et, après avoir tiré la force constante par ajustement par les moindres carrés, l'extension peut être prédite à partir de la loi de Hooke.
En analyse de régression du modèle est souvent une question empirique. Par exemple, un modèle très commun est le modèle de ligne droite qui est utilisée pour tester se il ya une relation linéaire entre la variable dépendante et indépendante. Si une relation linéaire est conclu à l'existence, sont dits être les variables corrélées . Toutefois, il est bien connu que la corrélation ne prouve pas la causalité, comme deux variables peuvent être corrélées avec d'autres, variables cachées. Par exemple, il existe une corrélation entre les décès par noyade et le volume des ventes de crème glacée. Tant le nombre de gens qui vont nager et le volume de glace augmentation des ventes de crème que le temps devient plus chaud et on peut supposer que le nombre de décès par noyade en corrélation avec le nombre de gens qui vont nager.
Dans les deux procédés, il est généralement supposé que la variable indépendante est exempte d'erreurs, mais que la variable dépendante est soumis à l'erreur expérimentale,  .
.
Dans cette expression de la valeur du modèle est présumée se rapprocher de la valeur réelle, ce est la valeur qui serait observé se il n'y avait pas d'erreur. On suppose que l'erreur ε est un expérimental variable aléatoire de moyenne nulle, ce est-il exclut toutes les erreurs d'un caractère systématique. Comme le modèle ne est qu'une approximation de la valeur réelle, les résidus sont conceptuellement différent des erreurs. Si la variable indépendante est sujette à l'erreur, moindres carrés totaux doivent être utilisés.
Afin de faire des tests statistiques sur les résultats, il est nécessaire de faire des hypothèses sur la nature des erreurs expérimentales. L'hypothèse la plus commune est que les erreurs font partie d'une distribution normale . Le théorème central limite soutient l'idée que ce est une bonne hypothèse dans de nombreux cas.
- Le Théorème de Gauss-Markov. Dans un modèle linéaire dans lequel les erreurs ont espérance nulle, sont non corrélés et ont les mêmes écarts , le meilleur linéaire estimateur non biaisé de toute combinaison linéaire des observations, est son estimateur des moindres carrés. "Best" signifie que les estimateurs des moindres carrés des paramètres ont variance minimale. L'hypothèse de l'égalité de la variance est valable lorsque les erreurs appartiennent tous à la même distribution.
- Dans un modèle linéaire, si les erreurs appartiennent à une distribution normale estimateurs des moindres carrés sont aussi les estimateurs du maximum de vraisemblance.
L'hypothèse selon laquelle les erreurs appartiennent à une fonction de distribution particulier ne est pas limitée à l'analyse de régression. En effet, ces hypothèses doivent être faites lors des tests statistiques sur les paramètres. Dans un calcul des moindres carrés avec des poids unitaires, ou dans la régression linéaire, la variance sur la j ème paramètre est donné par
Les limites de confiance peuvent être trouvés si la distribution de probabilité des paramètres est connu ou présumé. De même des tests statistiques sur les résidus peuvent être faites si la distribution de probabilité des résidus est connue ou supposée. La distribution de probabilité d'une combinaison linéaire des variables dépendantes peut être déduite si la distribution de probabilité des erreurs expérimentales est connue ou supposée. Le plus souvent, on suppose que les erreurs expérimentales appartiennent à une distribution normale. Dans ce cas, il est souvent supposé que les paramètres et les résidus appartiennent à une Loi de Student .
La somme des carrés des résidus peut être exprimé en
La matrice 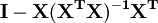 est une matrice symétrique idempotente de rang mn. Voici un exemple de l'utilisation de ce fait dans la théorie de la régression linéaire. Les valeurs propres d'une matrice d'idempotent sont 0 ou 1. Par conséquent, les valeurs propres de la matrice Mn ce sont égaux à 1 et n valeurs propres sont égales à zéro. Ce est la plupart du travail à démontrer que la somme des carrés des résidus a une distribution chi-carré avec des degrés de liberté mn.
est une matrice symétrique idempotente de rang mn. Voici un exemple de l'utilisation de ce fait dans la théorie de la régression linéaire. Les valeurs propres d'une matrice d'idempotent sont 0 ou 1. Par conséquent, les valeurs propres de la matrice Mn ce sont égaux à 1 et n valeurs propres sont égales à zéro. Ce est la plupart du travail à démontrer que la somme des carrés des résidus a une distribution chi-carré avec des degrés de liberté mn.
Pondérées moindres carrés
Les expressions données ci-dessus sont basées sur l'hypothèse implicite que toutes les mesures ne sont pas corrélées et ont égale incertitude. Le Gauss-Markov montre que, lorsqu'il en est ainsi, 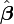 est un meilleur estimateur linéaire sans biais (BLEU). Si, toutefois, les mesures ne sont pas corrélées mais ont des incertitudes, une approche modifiée doit être adoptée. Aitken a montré que lorsque la somme pondérée des carrés des résidus soit minimisée,
est un meilleur estimateur linéaire sans biais (BLEU). Si, toutefois, les mesures ne sont pas corrélées mais ont des incertitudes, une approche modifiée doit être adoptée. Aitken a montré que lorsque la somme pondérée des carrés des résidus soit minimisée, 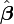 est bleu si chaque poids est égal à l'inverse de la variance de la mesure.
est bleu si chaque poids est égal à l'inverse de la variance de la mesure.
Les équations de gradient pour cette somme des carrés sont
qui, dans un système des moindres carrés linéaire donner les équations normales modifiés
ou
Lorsque les erreurs d'observation ne sont pas corrélées la matrice de poids W, est diagonale. Si les erreurs sont corrélées, la matrice de poids doit être égal à l'inverse de la matrice de variance-covariance des observations, mais cela ne affecte pas l'expression de la matrice des équations normales et les estimations de paramètres sont encore BLEU. Voir Moindres carrés généralisés pour plus de détails.
Lorsque les erreurs ne sont pas corrélées, il est commode de simplifier les calculs pour tenir compte de la matrice de poids 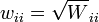 . Les équations normales peuvent alors être écrites comme
. Les équations normales peuvent alors être écrites comme
Pour les systèmes non linéaires des moindres carrés un argument similaire montre que les équations normales doivent être modifiées comme suit.
D'autres méthodes
Estimation des moindres carrés pour les modèles linéaires est notoirement non-robuste pour aberrantes. Si la distribution des valeurs aberrantes est biaisé, les estimations peuvent être biaisées. En présence de valeurs aberrantes, les estimations des moindres carrés sont inefficaces et peuvent être extrêmement lente. Lorsque les valeurs aberrantes se produisent dans les données, les méthodes de régression robuste sont plus appropriés.
La technique de moindres carrés partiels gagne en popularité dans chimiométrie et d'autres disciplines. Il est utilisé lorsque le modèle est partiellement connus et partiellement inconnue.
Les paramètres de régression peuvent également être estimées par Méthodes bayésiennes. Cela présente les avantages que
- les intervalles de confiance peuvent être produites pour les estimations des paramètres sans l'utilisation d'approximations asymptotiques,
- information préalable peut être incorporé dans l'analyse.
Dans la régression linéaire,
supposons que nous savons de la connaissance de domaine 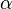 ne peut prendre l'une des valeurs {-1, 1}, mais nous ne savons pas qui. Nous pouvons construire cette information dans l'analyse en choisissant un préalable pour
ne peut prendre l'une des valeurs {-1, 1}, mais nous ne savons pas qui. Nous pouvons construire cette information dans l'analyse en choisissant un préalable pour 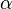 qui est une distribution discrète avec une probabilité de 0,5 à 0,5 sur 1 et 1. Le postérieure pour
qui est une distribution discrète avec une probabilité de 0,5 à 0,5 sur 1 et 1. Le postérieure pour 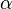 sera également une distribution discrète sur {-1, 1}, mais les poids de probabilité vont changer pour refléter les éléments de preuve à partir des données.
sera également une distribution discrète sur {-1, 1}, mais les poids de probabilité vont changer pour refléter les éléments de preuve à partir des données.
Méthode Lasso
Dans certains contextes, une Version régularisé de la solution des moindres carrés peut être préférable. L'algorithme LASSO, par exemple, trouve une solution des moindres carrés avec la contrainte que  , Le L 1 -norme du vecteur de paramètre, ne est pas supérieure à une valeur donnée. Équivalente, il peut résoudre une minimisation sans contrainte de la peine moindres carrés avec
, Le L 1 -norme du vecteur de paramètre, ne est pas supérieure à une valeur donnée. Équivalente, il peut résoudre une minimisation sans contrainte de la peine moindres carrés avec  ajoutée, où
ajoutée, où 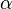 est une constante. (Ceci est le Lagrangien double problème de la contrainte.) Ce problème peut être résolu en utilisant programmation quadratique ou plus générale méthodes d'optimisation convexe. La formulation -regularized L 1 est utile dans certains contextes, en raison de sa tendance à préférer des solutions ayant moins de valeurs de paramètres non nuls, ce qui réduit efficacement le nombre de variables sur lesquelles la solution donnée est dépendante.
est une constante. (Ceci est le Lagrangien double problème de la contrainte.) Ce problème peut être résolu en utilisant programmation quadratique ou plus générale méthodes d'optimisation convexe. La formulation -regularized L 1 est utile dans certains contextes, en raison de sa tendance à préférer des solutions ayant moins de valeurs de paramètres non nuls, ce qui réduit efficacement le nombre de variables sur lesquelles la solution donnée est dépendante.
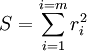
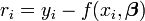
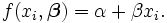

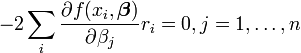


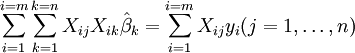
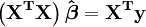

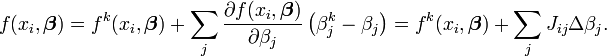



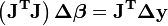
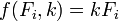



![\ Sigma ^ 2 (\ beta_j) = \ frac {S} {mn} \ left (\ left [X ^ TX \ right] ^ {- 1} \ right) _ {} jj.](../../images/203/20359.png)