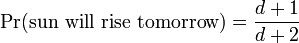Pierre-Simon Laplace

Pierre-Simon, marquis de Laplace
Portrait posthume de Mme Feytaud, 1842
Né	23/03/1749 Beaumont-en-Auge, Normandie, France
Mort	5 mars 1827 (05/03/1827) (77 ans) Paris , France
Résidence	France
Citoyenneté	Français
Les champs	Astronomie Mathématiques
Institutions	École Militaire (1769-1776)
Connu pour	Travailler dans Mécanique Céleste L'équation de Laplace Laplace opérateur / Laplacien Transformation de Laplace

Pierre-Simon, marquis de Laplace ( 23 mars 1749 - 5 mars 1827 ) était un Français mathématicien et astronome dont le travail était crucial pour le développement de l'astronomie mathématique . Il a résumé et étendu le travail de ses prédécesseurs dans son cinq volumes Mécanique Céleste ( Mécanique Céleste) (1799-1825). Cet ouvrage magistral traduit le géométrique étude mécanique classique , utilisé par Isaac Newton , l'une fondée sur le calcul , l'ouverture d'un plus large éventail de problèmes.

Il a formulé L'équation de Laplace, et a inventé le Transformée de Laplace qui apparaît dans de nombreuses branches de la physique mathématique , un champ qu'il a pris un rôle de premier plan dans la formation. Le Opérateur différentiel de Laplace, largement utilisé dans les appliqués de mathématiques , est également nommé d'après lui.

Indépendamment de Immanuel Kant , il a formulé le hypothèse de nébuleuse de la origine du système solaire et a été l'un des premiers scientifiques à postuler l'existence d' trous noirs et la notion de effondrement gravitationnel.

Il est connu comme l'un des plus grands scientifiques de tous les temps, parfois appelé un Français Newton Newton ou de la France, avec une faculté mathématique phénoménale naturel possédé par aucun de ses contemporains.

Il est devenu un compter de la Premier Empire français en 1806 et a été nommé marquis en 1817, après la Bourbon Restauration.

Jeunesse

Pierre Simon Laplace est né en Beaumont-en-Auge, Normandie.

Selon Rouse Ball ("Un compte à court de l'histoire des mathématiques», 4ème édition, 1908), il était le fils d'un petit propriétaire de chalet ou peut-être un ouvrier agricole, et devait son éducation à l'intérêt excité dans certains riches voisins par ses capacités et la présence engageante. Très peu est connu de ses premières années, quand il est devenu distingué qu'il avait la mesquinerie de se tenir à l'écart à la fois de ses parents et de ceux qui l'avaient aidé. Il semblerait, d'après un élève, il est devenu un huissier à l'école de Beaumont; mais, se étant procuré une lettre d'introduction à d'Alembert, il est allé à Paris pour pousser sa fortune. Toutefois, Pearson (1929, Biometrika) est cinglant sur les inexactitudes dans le compte de Rouse Ball et affirme que ".. Caen était probablement à l'époque de Laplace la plus intellectuellement active de toutes les villes de Normandie. Ce est là que Laplace a fait ses études et a été provisoirement un professeur. Ce est ici Il a écrit son premier article publié dans les Mélanges de la Société royale de Turin, Tome IV. 1766-1769, au moins deux ans avant de se rendre à 22 ou 23 à Paris en 1771. Ainsi, avant il était de 20 il était en contact avec Joseph Louis Lagrange dans Turin . Il ne va pas à Paris un garçon de la campagne autodidacte première avec seulement un paysan contexte, je En 176S à l'âge de seize ans Laplace quitté "l'école du duc d'Orléans" à Beaumont et est allé à l'Université de Caen, où il apparaît avoir étudié pendant cinq ans. Le "militaire de l'Ecole" de Beaumont n'a pas remplacé la vieille école jusqu'en 1770.

Son père était Pierre Laplace, un cidre marchand et sa mère était Marie-Anne Sochon. Ses parents étaient d'être confortable familles bourgeoises. Laplace a fréquenté une école dans la perspective du village à une Bénédictin prieuré, son père l'intention qu'il serait ordonné dans l' Eglise catholique romaine , et à seize ans il a été envoyé pour faire avancer l'intention de son père à la Université de Caen, lecture la théologie.

A l'université, il a été encadré par deux enseignants enthousiastes de mathématiques, Christophe Gadbled et Pierre Le Canu, qui éveillaient son zèle pour le sujet. Laplace jamais diplômé en théologie, mais parti pour Paris avec une lettre d'introduction de Le Canu à Jean le Rond d'Alembert. Il ya une histoire apocryphe, âgé de dix-neuf ans, il a résolu le problème du jour au lendemain que D'Alembert lui fixée pour la présentation de la semaine suivante, puis résolu un problème plus difficile la nuit suivante. D'Alembert a été impressionné et lui a recommandé pour un lieu d'enseignement dans le École Militaire.

Avec un revenu sûr et d'enseignement peu exigeante, Laplace se jeta en maintenant recherche originale et, dans les dix-sept prochaines années, 1771-1787, il a produit beaucoup de son œuvre originale en astronomie.

Laplace plus impressionné le Marquis de Condorcet, et même en 1771 Laplace a estimé qu'il avait droit à l'adhésion dans le Académie française des sciences. Toutefois, cette année, est allé à l'admission Alexandre-Théophile Vandermonde et en 1772 à Antoine-Joseph Cousin. Laplace était mécontent et au début de 1773 a sondé un passage à Berlin . Cependant, Condorcet est devenu secrétaire permanent de l'Académie en Février et Laplace a été élu membre associé 31 Mars.

Il se est marié en 1788 et son fils est né en 1789.

Analyse, de la probabilité et de la stabilité astronomique

Premiers travaux de Laplace publié en 1771 a commencé avec des équations différentielles et différences finies, mais il était déjà en train de réfléchir sur les concepts mathématiques et philosophiques de probabilité et statistiques . Toutefois, avant son élection à l'Académie en 1773, il avait déjà rédigé deux documents qui permettraient d'établir sa réputation. La première, Mémoire sur la Probabilité des provoque Les Événements PAR a été finalement publié en 1774 tandis que le second document, publié en 1776, plus élaboré sa pensée statistiques et a également commencé son travail systématique la mécanique céleste et la stabilité du système solaire . Les deux disciplines seraient toujours liés dans son esprit. "Laplace a pris la probabilité comme un instrument pour la réparation des défauts dans la connaissance." Le travail de Laplace sur la probabilité et les statistiques est discuté ci-dessous avec son œuvre de maturité sur la théorie analytique des probabilités.

La stabilité du système solaire

Sir Isaac Newton avait publié son Philosophiae Naturalis Principia Mathematica en 1687 dans lequel il a donné une dérivation de lois de Kepler , qui décrivent le mouvement des planètes , de ses lois du mouvement et son la loi de la gravitation universelle. Cependant, bien que Newton avait privé développé les méthodes de calcul , tout son travail publié utilisé lourde géométrique raisonnement, inapte à tenir compte des effets d'ordre supérieur plus subtiles d'interactions entre les planètes. Newton lui-même avait douté de la possibilité d'une solution mathématique à l'ensemble, même conclure que périodique intervention divine était nécessaire pour garantir la stabilité du système solaire. Dispense de l'hypothèse d'une intervention divine serait la principale activité de la vie scientifique de Laplace. En 2007, il est généralement considéré que les méthodes de Laplace sur leur propre, quoique essentielles au développement de la théorie, ne sont pas suffisamment précis pour démontrer la stabilité du système solaire.

Un problème particulier de astronomie observationnelle était l'instabilité apparente lequel Jupiter l 'orbite semblait se réduire tandis que celle de Saturne était en expansion. Le problème avait été abordé par Leonhard Euler en 1748 et Joseph Louis Lagrange en 1763, mais sans succès. En 1776, Laplace a publié un mémoire dans lequel il a d'abord exploré les influences possibles d'une prétendue éther lumineux ou d'une loi de la gravitation qui ne ont pas agir instantanément. Il a finalement retourné à un investissement intellectuel dans la gravitation newtonienne. Euler et Lagrange avaient fait une approximation pratique en ignorant petits termes dans les équations du mouvement. Laplace a noté que, bien que les termes eux-mêmes étaient de petite taille, lorsque intégré sur le temps qu'ils pourraient devenir importante. Laplace effectué son analyse dans les termes d'ordre supérieur, jusqu'à et y compris la cubique. Grâce à cette analyse plus exacte, Laplace a conclu que les deux planètes et le soleil doivent être en équilibre mutuel et ainsi lancé ses travaux sur la stabilité du système solaire. Gerald James Whitrow décrit la réalisation de «l'avancée la plus importante en astronomie physique depuis Newton".

Laplace avait une grande connaissance de toutes les sciences et a dominé toutes les discussions dans l'Académie. Laplace semble avoir considéré l'analyse simplement comme un moyen de se attaquer à des problèmes physiques, bien que la capacité avec laquelle il a inventé l'analyse nécessaire est presque phénoménale. Tant que ses résultats étaient vraies, mais il a peu de mal à expliquer les étapes par lesquelles il est arrivé à eux; il n'a jamais étudié l'élégance ou la symétrie dans ses processus, et ce était suffisant pour lui se il pouvait par tous les moyens de résoudre la question particulière qu'il discutait.

Sur la figure de la Terre

Pendant les années 1784-1787, il a produit des mémoires de puissance exceptionnelle. Au premier rang de ceux-ci est une lecture en 1783, réimprimé comme la partie II de Théorie du Mouvement et de la figure elliptique des planètes en 1784, et dans le troisième volume de la Méchanique céleste. Dans ce travail, Laplace complètement déterminé l'attrait d'un sphéroïde sur une particule à l'extérieur. Ce est mémorable pour l'introduction dans l'analyse des harmoniques sphériques ou de Laplace de coefficients, et également pour le développement de l'utilisation de la potentiel, un nom d'abord utilisé par George Green en 1828.

Harmoniques sphériques

Harmoniques sphériques

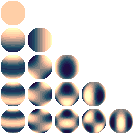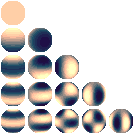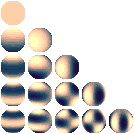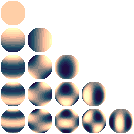
En 1783, dans un document envoyé à l'Académie, Adrien-Marie Legendre avait introduit ce qui est maintenant connu sous le nom fonctions de Legendre. Si deux points dans un plan sont coordonnées polaires (r, θ) et (r ', θ'), où r '≥ r, puis, par une manipulation élémentaire, l'inverse de la distance entre les points, d, peut être écrite comme:

Cette expression peut être élargi en puissances de r / r 'aide Binôme de Newton généralisée pour donner:

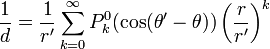
La séquence de fonctions P ⁰ _k (cosф) est l'ensemble de ce qu'on appelle "fonctions de Legendre associées» et leur utilité vient du fait que chaque fonction des points sur un cercle peut être étendu comme un série d'entre eux.

Laplace, au mépris de crédit pour Legendre, a fait l'extension non-triviale du résultat trois dimensions pour donner un ensemble plus général de fonctions, les harmoniques sphériques ou des coefficients de Laplace. En 2007, ce dernier terme ne est pas d'usage courant. Chaque fonction des points d'une sphère peut être étendue en une série d'entre eux.

La théorie du potentiel

Ce document est également remarquable pour le développement de l'idée de la potentiel scalaire. Le gravitationnelle vigueur agissant sur un corps est, en langage moderne, un vecteur , ayant ampleur et la direction. Un potentiel est une fonction fonction scalaire qui définit comment les vecteurs vont se comporter. Une fonction scalaire est de calcul et conceptuellement plus facile à traiter que d'une fonction de vecteur.

Alexis Clairaut avait d'abord suggéré l'idée en 1743 tout en travaillant sur un problème similaire se il utilisait de type newtonien raisonnement géométrique. Laplace a décrit le travail de Clairault comme étant "dans la classe des plus belles productions les mathématiques". Cependant, Rouse boule allègue que l'idée "a été prélevé sur Joseph Louis Lagrange , qui avait utilisé dans ses mémoires de 1773, 1777 et 1780 ".

Laplace appliquée la langue de calcul de la fonction de potentiel et montre qu'elle satisfait toujours l' équation différentielle :

- Et sur ce résultat de son travail ultérieur sur l'attraction gravitationnelle était fondée. La quantité 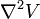qui a été appelé la concentration de et sa valeur à tout point indique le «excès» de la valeur de là sur sa valeur moyenne dans le voisinage du point. L'équation de Laplace, un cas particulier de L'équation de Poisson, apparaît ubiquitaire dans la physique mathématique. Partout où une force de vecteur actes sur un corps, le concept d'un potentiel peuvent être appliquées et l'équation de Laplace se produit dans la dynamique des fluides, l'électromagnétisme et d'autres domaines. Selon certains auteurs cela résulte à la fois du fait que 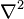est un opérateur scalaire. Rouse boule spéculé qu'il pourrait être considéré comme "le signe extérieur" d'un des "formes antérieures» dans la théorie kantienne de la perception .

Les harmoniques sphériques se avérer critique pour des solutions pratiques de l'équation de Laplace. L'équation de Laplace en coordonnées sphériques , tels que ceux utilisés pour la cartographie du ciel, peut être simplifiée, en utilisant la méthode de séparation des variables dans une partie radiale, en fonction uniquement de la distance de la terre (par exemple), et une partie angulaire ou sphérique. La solution de la partie sphérique de l'équation peut être exprimée comme une série d'harmoniques sphériques de Laplace, ce qui simplifie le calcul pratique.

Inégalités planétaires

Ce mémoire a été suivie d'une autre sur les inégalités planétaires, qui a été présenté en trois sections en 1784, 1785 et 1786. Cette porte principalement sur l'explication de la "grande inégalité» de Jupiter et de Saturne. Laplace a montré par des considérations générales que l'action mutuelle des deux planètes ne pourrait jamais influer largement les excentricités et des inclinaisons de leurs orbites; et que les particularités du système jovien étaient dus à l'approche proche de proportionnalité des moyens mouvements de Jupiter et de Saturne: l'évolution de ces théorèmes sur le mouvement des planètes ont été donnés dans ses deux mémoires de 1788 et 1789. Ce est sur ces données Delambre calculé ses tables astronomiques.

Il avait été observé depuis les temps anciens que la Lune position de l 'dans le ciel était à la dérive au fil du temps. En 1693, Edmond Halley avait montré que le taux de la dérive augmente, un effet connu comme l'accélération séculaire de la Lune. Laplace a donné une explication en 1787 en termes de changements dans le excentricité de l'orbite de la Terre. Cependant, en 1853, John Couch Adams a continué à montrer que Laplace ne avait examiné que la force radiale sur la lune et non la tangentielle, et donc ne avait pas expliqué plus de la moitié de la dérive. L'autre moitié a été montré par la suite être due à l'accélération de marée. Cependant, Laplace était encore capable d'utiliser son résultat pour compléter la preuve de la la stabilité de l'ensemble du système solaire dans l'hypothèse où il est constitué d'une collection de corps rigides se déplacent dans un vide.

Tous les mémoires ci-dessus fait allusion à été présenté à l'Académie des sciences, et ils sont imprimés dans les Mémoires PRESENTES PAR divers savants.

La mécanique céleste

Laplace se mit maintenant la tâche d'écrire une œuvre qui doit "offrir une solution complète de la grande problème mécanique présenté par le système solaire , et faire coïncider la théorie si étroitement avec l'observation que les équations empiriques ne devraient plus trouver une place dans les tables astronomiques. " Le résultat se incarne dans l'Exposition du système du monde et de la Mécanique céleste de.

Le premier a été publié en 1796, et donne une explication générale du phénomène, mais omet tous les détails. Il contient un résumé de l'histoire de l'astronomie. Ce résumé acquis pour son auteur l'honneur d'admission à la quarante de l'Académie française et est couramment estimé l'un des chefs-d'œuvre de la littérature française, si ce ne est pas tout à fait fiable pour les périodes ultérieures dont il traite.

Laplace a développé le hypothèse de nébuleuse de la formation du système solaire, d'abord suggéré par Emanuel Swedenborg et élargies par Emmanuel Kant , une hypothèse qui continue de dominer les comptes de l'origine des systèmes planétaires. Selon la description de Laplace de l'hypothèse, le système solaire a évolué à partir d'une masse globulaire de incandescent gaz tournant autour d'un axe passant par son centre de masse . Comme il refroidi cette masse contracté et anneaux successifs rompu de son bord extérieur. Ces anneaux à leur tour refroidis, et enfin condensés dans les planètes , tandis que le soleil représente le noyau central qui a été toujours à gauche. Sur ce point de vue Laplace prédit que les planètes plus éloignées seraient plus âgés que ceux plus près du soleil.

L'idée de l'hypothèse de la nébuleuse avait été décrite par Emmanuel Kant en 1755, et il avait aussi suggéré "agrégations météoriques» et frottement des marées comme causes affectant la formation du système solaire. Il est probable que Laplace ne était pas au courant de cela.

Discussion analytique de Laplace du système solaire est donnée dans son céleste de Méchanique publié en cinq volumes. Les deux premiers volumes, publiés en 1799, contiennent des méthodes de calcul des mouvements des planètes, la détermination de leurs chiffres, et résoudre les problèmes de marée. Les troisième et quatrième volumes, publiés en 1802 et 1805, contiennent des applications de ces méthodes, et plusieurs tables astronomiques. Le cinquième volume, publié en 1825, est principalement historique, mais il donne en annexe les résultats des dernières recherches de Laplace. Propres enquêtes de Laplace qui y sont contenus sont si nombreux et précieux qu'il est regrettable d'avoir à ajouter que de nombreux résultats sont affectés d'écrivains avec rares ou aucun accusé de réception, et les conclusions - qui ont été décrits comme le résultat organisée d'un siècle de patient labeur - sont souvent mentionné comme si elles étaient dues à Laplace.

Jean-Baptiste Biot, qui a aidé à la révision de Laplace pour la presse, dit que Laplace lui-même était souvent incapables de récupérer les détails de la chaîne de raisonnement, et, se il est convaincu que les conclusions ont été correct, il était contenu à insérer le récurrent formule, "il est Aisé à voir." Le céleste Méchanique ne est pas seulement la traduction des Principia dans la langue de la calcul différentiel, mais il complète pièces dont Newton ne avait pu remplir dans les détails. Le travail a été plus fine par Félix Tisserand, mais le traité de Laplace resteront toujours une autorité standard.

La maison de Laplace à Arcueil

Arcueil

En 1806, Laplace a acheté une maison dans Arcueil, puis un village et non encore absorbé dans Paris agglomération. Claude Louis Berthollet était un proche voisin et la paire formée du noyau d'un milieu scientifique informelle, dernièrement connu comme la Société d'Arcueil. En raison de la proximité de Laplace et Berthollet à Napoléon , ils ont contrôlé efficacement l'avancement dans la création scientifique et l'admission aux bureaux les plus prestigieux. La Société construit un complexe de pyramide patronage.

La science comme la prédiction

Laplace est allé dans l'état de mendier Napoléon à accepter une copie de son travail, qui avait entendu dire que le livre contenait aucune mention de Dieu . Napoléon, qui aimait de poser des questions embarrassantes, reçut avec la remarque, "M. Laplace, ils me disent que vous avez écrit ce grand livre sur le système de l'univers, et ne ont jamais même mentionné son Créateur." Laplace, qui, bien que la plus souple des politiciens, était raide comme un martyr sur tous les points de sa philosophie, se redressa et a répondu sans ambages, "Je ne avais pas besoin de se this hypothèse-là." (Je ne ai pas besoin de faire une telle hypothèse). Napoléon, beaucoup amusé, dit cette réponse Lagrange, qui se écria: «Ah ce est une belle hypothèse;! Ça Explique beaucoup de choses" (Ah ce est une belle hypothèse;! Il explique beaucoup de choses). Laplace a ensuite déclaré: "Cette hypothèse, Sire, Explique en effet tout, Mais ne Permet de prédire rien En Tant que savant, je me Dois de vous provide des travaux permettant des prédictions." ("Cette hypothèse, Sire, ne explique pas tout, mais ne permet pas de rien prédire. En tant qu'universitaire, je dois vous fournir avec des œuvres permettant prédictions. »- Cité par Ian Stewart et Jack Cohen) Laplace la science ainsi défini comme un outil de prédiction..

Trous noirs

Laplace est également venu près de propager la le concept de trou noir . Il a souligné qu'il pourrait y avoir des étoiles massives dont la gravité est si grande que même la lumière ne peut échapper à leur surface (voir échapper à la vitesse). Laplace a également spéculé que certaines des nébuleuses révélé par les télescopes ne peuvent pas faire partie de la Voie Lactée et pourrait effectivement être galaxies elles-mêmes. Ainsi, il a anticipé la découverte majeure du Edwin Hubble, quelques 100 années avant que ça arrive.

Théorie analytique des probabilités

En 1812, Laplace a publié sa Théorie analytique des probabilités dans laquelle il stipulé nombreux résultats fondamentaux dans les statistiques . En 1819, il a publié un compte rendu populaire de son travail sur la probabilité. Ce livre porte le même rapport à la Théorie des probabilités que le Système du monde fait à l'céleste Méchanique.

Fonction génératrice des probabilités

Procédé d'estimation du rapport entre le nombre des cas favorables, par rapport au nombre total de cas possibles, avait déjà été indiqué par Laplace dans un document écrit en 1779. Elle consiste à traiter les valeurs successives de toute fonction que les coefficients de la l'expansion d'une autre fonction, en référence à une variable différente. Ce dernier est donc appelé fonction probabilité de génération de la première. Laplace montre comment, au moyen d' interpolation , ces coefficients peuvent être déterminés à partir de la fonction génératrice. Ensuite, il se attaque au problème inverse, et à partir des coefficients il trouve la fonction de production; ceci est effectué par la solution d'un équation de différence finie. La méthode est lourde et conduit la plupart du temps à une distribution de probabilité normale que l'on appelle répartition de Laplace-Gauss, à ne pas confondre avec le La distribution de Laplace.

Moindres carrés

Ce traité comprend un exposé de la méthode des moindres carrés , un témoignage remarquable de l'ordre de Laplace sur les processus d'analyse. La méthode des moindres carrés pour la combinaison de nombreuses observations avait été donné de manière empirique par Carl Friedrich Gauss et Legendre, mais le quatrième chapitre de cet ouvrage contient une preuve formelle de celui-ci, sur lequel se fonde depuis l'ensemble de la théorie des erreurs. Cela a été affectée que par une analyse plus complexe spécialement inventé pour le but, mais la forme dans laquelle il est présenté est si maigre et insuffisante que, en dépit de la précision uniforme des résultats, ce était à un moment demandé si Laplace avait fait passé par le travail difficile qu'il sorte brièvement et souvent incorrectement indique.

Probabilité inductive

Alors qu'il a effectué beaucoup de recherches en physique , un autre thème majeur des efforts de sa vie était la théorie des probabilités . Dans son Essai philosophique sur les probabilités, Laplace a établi un système mathématique de raisonnement inductif basé sur la probabilité , que nous serions aujourd'hui reconnaître comme Bayésien. Une formule bien connue découlant de son système est le règle de succession. Supposons que certains procès a que deux résultats possibles, étiqueté «succès» et «échec». Sous l'hypothèse que peu ou rien ne est connu a priori sur les vraisemblances relatives des résultats, Laplace dérivé une formule pour la probabilité que le prochain essai sera un succès.

où s est le nombre de succès observés précédemment et n est le nombre total d'essais observés. Il est encore utilisé comme un estimateur de la probabilité d'un événement si nous savons l'espace de l'événement, mais ne ont qu'un petit nombre d'échantillons.

La règle de la succession a fait l'objet de nombreuses critiques, en partie en raison de l'exemple que Laplace a choisi de l'illustrer. Il a calculé que la probabilité que le soleil se lèvera demain, étant donné qu'il n'a jamais manqué dans le passé, était

où d est le nombre de fois que le soleil a augmenté au cours des dernières heures. Ce résultat a été tourné en dérision aussi absurde, et certains auteurs ont conclu que toutes les demandes de la règle de succession sont absurdes par extension. Cependant, Laplace était pleinement conscient de l'absurdité du résultat; immédiatement après l'exemple, il a écrit: «Mais ce nombre [ce est à dire, la probabilité que le soleil se lèvera demain] est beaucoup plus grande pour celui qui, voyant dans l'ensemble des phénomènes du principe régissant les jours et les saisons, réalise que rien au moment présent peut arrêter le cours de celui-ci ".

Démon de Laplace

Laplace croyait fermement en déterminisme causal, qui est exprimée dans la citation suivante de l'introduction de l'Essai:

Cette intelligence est souvent désigné comme le démon de Laplace (dans la même veine que Le démon de Maxwell). A noter que la description de l'intellect hypothétique décrit ci-dessus en tant que Laplace démon ne vient pas de Laplace, mais de biographes ultérieurs: Laplace se voyait comme un scientifique qui espère que l'humanité progresser dans une meilleure compréhension scientifique du monde, qui, si et quand finalement achevé, aurait encore besoin d'une puissance de calcul énorme pour calculer tout cela en un seul instant.

Transformées de Laplace

Dès 1744, Euler, Lagrange suivie, avait commencé à chercher des solutions de équations différentielles sous la forme:

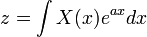et .

En 1785, Laplace a pris l'étape clé dans l'aide intégrales de cette forme afin de transformer l'ensemble équation aux différences, plutôt que simplement comme une forme pour la solution, et a constaté que l'équation transformée était plus facile à résoudre que l'original.

Autres découvertes et réalisations

Mathématiques

Parmi les autres découvertes de Laplace en mathématiques pures et sont applicables:

• Discussion, simultanément à Alexandre-Théophile Vandermonde, de la théorie générale des déterminants , (1772);
• Preuve que chaque équation d'un degré encore doit avoir au moins un réel facteur quadratique;
• Solution de l' équation aux dérivées partielles linéaire du second ordre;
• Il fut le premier à considérer les problèmes difficiles qui se posent dans les équations de différences mixtes, et de prouver que la solution d'une équation en différences finies du premier degré et du second ordre peut toujours être obtenue sous la forme d'un fraction continue; et
• Dans sa théorie des probabilités:
  • Évaluation de plusieurs communes intégrales définies ; et
  • La preuve générale de la Théorème d'inversion de Lagrange.

La tension de surface

Laplace repose sur le travail qualitatif des Thomas Young pour développer la théorie de une action capillaire et le Équation de Young-Laplace.

Vitesse du son

Laplace en 1816 fut le premier à souligner que la la vitesse du son dans l' air dépend de la rapport de capacité thermique. Théorie originale de Newton a donné une valeur trop faible, car il ne tient pas compte de la adiabatique compression de l'air qui se traduit par une élévation locale de la température et pression. Les enquêtes de Laplace en physique pratique ont été confinés à celles exercées par lui, conjointement avec Lavoisier dans les années 1782-1784 sur le chaleur spécifique de divers organismes.

Ambitions politiques

Comme la puissance de Napoléon augmenté Laplace le pria de lui donner le poste de ministre de l'Intérieur. Napoléon, qui voulait le soutien des hommes de science, a accepté la proposition, mais un peu moins de six semaines a vu la fin de la carrière politique de Laplace. Le mémorandum de Napoléon sur son licenciement est comme suit:

Géomètre de premier rang, Laplace ne tarda pas à se MONTRER administrateur médiocre, plus de file; Dès fils premier travail Nous reconnûmes Que Nous Nous étions trompé. Laplace ne saisissait Aucune question fils sous le point de vue de Véritable: il cherchait des subtilités partout, n'avait Que des Idées Problématiques, et portait enfin l'esprit des `infiniment petits» Jusque Dans l'administration. (Géomètre de premier rang, Laplace ne tarda pas à se montrer un administrateur pire que la moyenne, puisque ses premières actions dans le bureau, nous avons reconnu notre erreur Laplace n'a pas examiné toute question objective: il cherchait subtilités partout, les problèmes ne se conçoit, et enfin. porté l'esprit de "arguties" dans l'administration.)

Bien que Laplace a été démis de ses fonctions, il était souhaitable de conserver son allégeance. Il a donc été soulevée au Sénat, et le troisième volume de la Mécanique céleste qu'il préfixé une note de toutes les vérités qu'ils contiennent le plus précieux de l'auteur a été la déclaration il parlait ainsi de sa dévotion envers le pacificateur de l'Europe. Dans exemplaires vendus après la Bourbon Restauration cela a été radiée. En 1814, il était évident que l'empire tombait; Laplace se empressa d'offrir ses services à la Bourbons, et sur la restauration a été récompensé avec le titre de marquis. Le mépris que ses collègues plus honnêtes estimé pour sa conduite en la matière peut être lu dans les pages de Paul Louis Courier. Sa connaissance était utile sur les nombreuses commissions scientifiques sur lesquelles il a servi, et représente probablement la manière dont son manque de sincérité politique a été négligée; mais la petitesse de son caractère ne doit pas nous faire oublier à quel point étaient ses services à la science.

Il est mort à Paris en 1827.

Honneurs

• Astéroïde 4628 Laplace est appelé pour lui.
• Il est l'un de seulement soixante-douze personnes d'avoir leurs noms sur la Tour Eiffel.

Citations

Wikiquote a une collection de citations liées à: Pierre-Simon Laplace

• Ce que nous savons, ce est pas beaucoup. Ce que nous ne savons pas est immense. (Attribué)
• Je ne avais pas besoin de cette hypothèse. ("Je ne avais pas besoin de se this hypothèse-là", comme une réponse à Napoléon , qui avait demandé pourquoi il ne avait pas mentionné Dieu dans son livre sur l'astronomie )
• "Il est donc évident que ..." (souvent utilisé dans la mécanique céleste quand il avait prouvé quelque chose et la preuve égarés ou trouvés il maladroit. Notorious comme un signal pour quelque chose de vrai, mais difficile à prouver.)
• Le poids de la preuve pour une affirmation extraordinaire doit être proportionnée à son étrangeté. (Connu sous le Principe de Laplace)