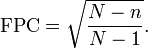Marge d'erreur
Contexte des écoles Wikipédia
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?
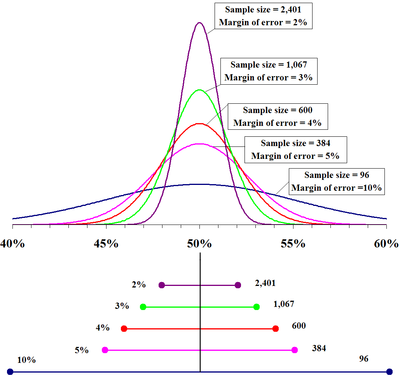
La marge d'erreur est une statistique exprimant le montant de hasard l'erreur d'échantillonnage dans un Les résultats de l'enquête. Plus la marge d'erreur, moins confiance que l'on doit avoir que les résultats rapportés du sondage sont proches des «vrais» chiffres; ce est, les chiffres pour l'ensemble population.
Explication
La marge d'erreur est habituellement défini comme le un rayon de intervalle de confiance pour un particulier statistique d'une enquête. Un exemple est le pour cent des personnes qui préfèrent produit A par rapport au produit B. Quand une marge unique mondiale d'erreur est signalée pour une enquête, il se réfère à la marge d'erreur maximale pour tous signalés pourcentages en utilisant l'échantillon complet de l'enquête. Si la statistique est un pourcentage, cette marge d'erreur maximale peut être calculée comme le rayon de l'intervalle de confiance pour un pourcentage de 50% rapporté.
La marge d'erreur a été décrite comme une quantité "absolue", égale à un rayon intervalle de confiance pour la statistique. Par exemple, si la valeur réelle est 50 points de pourcentage, et la statistique a un rayon intervalle de confiance de 5 points de pourcentage, alors nous disons la marge d'erreur est de 5 points de pourcentage. Comme autre exemple, si la valeur réelle est de 50 personnes, et la statistique a un rayon intervalle de confiance de 5 personnes, alors nous pourrions dire la marge d'erreur est de 5 personnes.
Dans certains cas, la marge d'erreur ne est pas exprimé comme une quantité "absolue"; plutôt il est exprimé comme une quantité «parent». Par exemple, supposons que la valeur réelle est de 50 personnes, et la statistique a un rayon intervalle de confiance de 5 personnes. Si nous utilisons la définition de «absolue», la marge d'erreur serait de 5 personnes. Si nous utilisons la définition de «parent», nous exprimons cette marge d'erreur absolue comme un pour cent de la valeur réelle. Donc dans ce cas, la marge d'erreur absolue est de 5 personnes, mais le «pour cent par rapport« marge d'erreur est de 10% (parce que cinq personnes sont dix pour cent de 50 personnes). Souvent, cependant, la distinction ne est pas explicitement fait, mais est habituellement apparente à partir du contexte.
Comme les intervalles de confiance, la marge d'erreur peut être définie pour ne importe quel niveau de confiance souhaité, mais généralement un niveau de 90%, 95% ou 99% est choisi (généralement 95%). Ce niveau est le probabilité qu'une marge d'erreur autour du pourcentage déclaré inclurait la «vraie» pourcentage. Avec le niveau de confiance, le plan d'échantillonnage pour une enquête, et en particulier son taille de l'échantillon, détermine l'amplitude de la marge d'erreur. Un échantillon plus grand produit une marge d'erreur plus faible, toutes choses égales par ailleurs.
Si les intervalles de confiance exacts sont utilisés, la marge d'erreur prend en compte à la fois l'erreur d'échantillonnage et l'erreur non-échantillonnage. Si un intervalle de confiance approximatif est utilisé (par exemple, en supposant que la distribution est normale, puis la modélisation de l'intervalle de confiance en conséquence), la marge d'erreur ne peut prendre aléatoire l'erreur d'échantillonnage en compte. Il ne représente pas d'autres sources potentielles d'erreurs ou de polarisation tel qu'un échantillon de configuration non représentatif, des questions mal formulées, les gens mentent ou refusant de répondre, l'exclusion des personnes qui ne ont pas pu être contactés, ou erreur de comptage et des erreurs de calcul.
Concept
Exemple Exécution
Un exemple allant de la 2004 campagne présidentielle américaine sera utilisée pour illustrer les concepts dans cet article. Selon un 2 octobre 2004 par enquête Newsweek, 47% des électeurs inscrits voterait pour John Kerry / John Edwards, si l'élection avait lieu ce jour-là, 45% voteraient pour George W. Bush / Dick Cheney, et 2% voteraient pour Ralph Nader / Peter Camejo. Le taille de l'échantillon était de 1,013. Sauf indication contraire, le reste de cet article utilise un niveau de confiance de 95%.
Concept de base
Sondages impliquent généralement prélever un échantillon d'une certaine population. Dans le cas du sondage de Newsweek, la population d'intérêt est la population de personnes qui voteront. Parce qu'il est impossible d'interroger tous ceux qui vont voter, sondeurs prennent des échantillons plus petits qui sont destinés à être représentatif; c'est un échantillon aléatoire de la population. Il est possible que les sondeurs échantillonnent 1013 électeurs qui arrivent à voter pour Bush alors qu'en fait, la population est répartie également entre Bush et Kerry, mais ce est extrêmement improbable (p = 1,13923782 ≈ 2 -1 013 × 10 -305) étant donné que l'échantillon est aléatoire.
théorie de l'échantillonnage fournit des méthodes de calcul de la probabilité que les résultats du sondage diffèrent de la réalité de plus d'un certain montant, tout simplement due au hasard; par exemple, que le sondage rapporte 47% pour Kerry, mais son soutien est en fait aussi élevée que 50%, ou est vraiment aussi bas que 44%. Cette théorie et certaines Bayésiens hypothèses suggèrent que le "vrai" pourcentage sera probablement assez proche de 47%. Plus les gens qui sont échantillonnées, les sondeurs peuvent être plus confiants que le "vrai" pourcentage est proche du pourcentage observé. La marge d'erreur est une mesure de l'écart entre les résultats sont susceptibles d'être.
Toutefois, la marge d'erreur ne représente que l'erreur d'échantillonnage aléatoire, il est aveugle à des erreurs systématiques qui peuvent être introduits par non-réponse ou par les interactions entre l'enquête et de la mémoire, la motivation, la communication de sujets et de connaissances.
Calculs suppose un échantillonnage aléatoire
Cette section aborde brièvement la erreur-type d'un pourcentage, le intervalle de confiance correspondant, et relier ces deux concepts à la marge d'erreur. Pour plus de simplicité, les calculs supposent ici le scrutin a été basée sur un échantillon aléatoire simple à partir d'une grande population.
L'erreur-type d'une proportion ou le pourcentage rapporté p mesure sa précision, et est l'écart type estimé de ce pourcentage. Il peut être estimé à partir de seulement p et la taille de l'échantillon, n, si n est faible par rapport à la taille de la population, en utilisant la formule suivante:
- Erreur type =
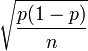
Lorsque l'échantillon ne est pas un échantillon aléatoire simple à partir d'une grande population, l'erreur standard et l'intervalle de confiance doit être estimée par des calculs plus avancés. Dans la plupart des cas, l'intervalle de confiance réelle est évaluée en supposant la distribution est normale, et inputing l'intervalle. Pour les distributions normales, les rayons de l'intervalle de confiance est proportionnelle à l'erreur-type. Habituellement, la véritable erreur-type est inconnue, erreur-type d'une estimation est calculée à partir de données de l'échantillon.
Notez qu'il n'y a pas nécessairement un lien étroit entre le vrai intervalle de confiance, et la véritable erreur de standard. L'intervalle de confiance pour cent de p-vrai est l'intervalle [a, b] qui contient p pour cent de la distribution, et où (100-p) / 2 pour cent de la distribution est inférieure à une, et (100-p) / 2 pour cent de la distribution est supérieure à b. La véritable erreur standard de la statistique est la racine carrée de la variance d'échantillonnage de la statistique. Ces deux ne peuvent pas être directement liée, même si en général, pour les grandes distributions qui ressemblent courbes normales, il existe une relation directe.
Dans le sondage de Newsweek, le niveau de soutien p = 0,47 de Kerry et n = 1013. L'erreur standard (0,016 ou 1,6%) contribue à donner un sens de l'exactitude de la pourcentage estimé de Kerry (47%). Un Interprétation bayésienne de l'erreur-type, ce est que même si nous ne savons pas le "vrai" pourcentage, il est très susceptible d'être situé dans les deux erreurs standard du pourcentage estimé (47%). L'erreur standard peut être utilisé pour créer un intervalle de confiance à l'intérieur duquel la «vraie» pourcentage devrait être à un certain niveau de confiance.
Le pourcentage estimé plus ou moins sa marge d'erreur est un intervalle de confiance pour le pourcentage. En d'autres termes, la marge d'erreur est la moitié de la largeur de l'intervalle de confiance. Il peut être calculé comme un multiple de l'écart type, le facteur dépendant du niveau de confiance désiré; une marge d'une erreur-type donne un intervalle de confiance de 68%, tandis que le plus les estimation ou moins 1,96 écarts-types est un intervalle de confiance de 95%, et un intervalle de confiance de 99% exécute 2,58 écarts-types de chaque côté de l'estimation.
Définition
La marge d'erreur pour une statistique d'intérêt particulier est habituellement défini comme le rayon (ou la moitié de la largeur) de l'intervalle de confiance pour cette statistique. Le terme peut également être utilisé pour signifier l'erreur d'échantillonnage en général. Dans les rapports des médias sur les résultats du sondage, le terme se réfère généralement à la marge d'erreur maximale pour un pourcentage de ce sondage.
Marge d'erreur maximale
La marge d'erreur maximale pour chaque pourcentage est le rayon de l'intervalle de confiance quand p = 50%. En tant que tel, il peut être calculé directement à partir du nombre de répondants sondage. Pour 95% de confiance, en supposant une échantillon aléatoire simple à partir d'une grande population:
- Marge (maximum) d'erreur (95%) = 1,96 ×
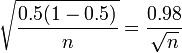
Ce calcul donne une marge d'erreur de 3% pour le sondage de Newsweek, qui a enregistré une marge d'erreur de 4%. La différence est probablement due à la pondération ou complexes caractéristiques de la conception de l'échantillonnage qui nécessitaient d'autres calculs de l'erreur standard. Il est également possible que Newsweek ont arrondi conservatrice à éviter de surévaluer la confiance de leurs résultats.
Différents niveaux de confiance
Pour un échantillon aléatoire simple à partir d'une grande population, la marge d'erreur maximale est une ré-expression simple de la taille de l'échantillon n. Les numérateurs de ces équations sont arrondis à deux décimales.
- Marge d'erreur de 99% de confiance
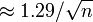
- La marge d'erreur à 95% de confiance

- La marge d'erreur à 90% de confiance

Si un article sur un sondage ne indique pas la marge d'erreur, mais ne indique qu'un échantillon aléatoire simple d'une certaine taille a été utilisée, la marge d'erreur peut être calculé pour un degré de confiance en utilisant l'une des formules ci-dessus souhaitée. En outre, si la marge d'erreur de 95% est donné, on peut trouver la marge d'erreur de 99% par augmentation de la marge d'erreur signalés par environ 30%.
Marges maximales et spécifiques de l'erreur
Bien que la marge d'erreur généralement rapporté dans les médias est une figure sondage à l'échelle qui reflète la variation d'échantillonnage maximale de tout pourcentage basé sur tous les répondants de ce sondage, la marge terme d'erreur se réfère également au rayon de l'intervalle de confiance pour un particulier statistique.
La marge d'erreur pour un pourcentage individu particulier sera généralement inférieure à la marge d'erreur maximale cité pour l'enquête. Ce maximum se applique uniquement lorsque le pourcentage observé est de 50%, et la marge d'erreur rétrécit à mesure que le pourcentage se rapproche des extrémités de 0% ou 100%.
En d'autres termes, l'erreur maximale de mesure est le rayon d'un intervalle de confiance de 95%, pour un pourcentage de 50% rapporté. Si p se écarte de 50%, l'intervalle de confiance de p sera plus courte. Ainsi, la marge d'erreur maximale représente une limite supérieure de l'incertitude; on est au moins certain à 95% que le "vrai" pourcentage est dans la marge d'erreur maximale d'un pourcentage indiqué pour ne importe quel pourcentage signalé.
Effet de la taille de la population
Les formules ci-dessus pour la marge d'erreur supposent qu'il existe un infiniment grand la population et donc ne dépendent pas de la taille de la population d'intérêt. Selon la théorie de l'échantillonnage , cette hypothèse est raisonnable lorsque le fraction d'échantillonnage est faible. La marge d'erreur pour une méthode d'échantillonnage particulière est essentiellement le même indépendamment du fait que la population d'intérêt est la taille d'une école, ville, état ou pays, aussi longtemps que la fraction d'échantillonnage est inférieure à 10%.
Dans les cas où la fraction d'échantillonnage est supérieure à 10%, les analystes peuvent ajuster la marge d'erreur en utilisant "la correction de la population finie," (FPC) pour tenir compte de la précision ajoutée acquise par échantillonnage à proximité d'un plus grand pourcentage de la population. FPC peut être calculée en utilisant la formule:
Pour tenir compte d'un grand taux d'échantillonnage, le FPC en compte dans le calcul de la marge d'erreur, ce qui a pour effet de réduire la marge d'erreur. Il soutient que la fpc approche de zéro que la taille de l'échantillon (n) se rapproche de la taille de la population (N), qui a pour effet d'éliminer la marge d'erreur entièrement. Ce est logique intuitive parce que quand N = n, l'échantillon devient un recensement et l'erreur d'échantillonnage devient sans objet.
Les analystes doivent être conscients que l'échantillon reste vraiment aléatoire que la fraction d'échantillonnage pousse, de peur biais d'échantillonnage être introduit.
Autres statistiques
Les intervalles de confiance peuvent être calculés, et peut donc des marges d'erreur, pour un éventail de statistiques, y compris les pourcentages individuels, les différences entre les pourcentages, des moyennes, des médianes et les totaux.
La marge d'erreur pour la différence entre deux pourcentages est plus grande que les marges d'erreur pour chacun de ces pourcentages, et peut même être plus grande que la marge d'erreur maximale pour un pourcentage quelconque personne de l'enquête.
Comparant les pourcentages
Dans un Scrutin uninominal majoritaire à un tour, il est important de savoir qui est en avance. Les termes «cravate statistique" et "chaleur morts statistique» sont parfois utilisés pour décrire les pourcentages indiqués qui diffèrent de moins de marge d'erreur, mais ces termes peuvent être trompeuses. Pour une chose, la marge d'erreur que généralement calculée est applicable à un pourcentage et non la différence entre les pourcentages, de sorte que la différence entre deux estimations de pourcentage peut ne pas être statistiquement significative même si elles diffèrent de plus de la marge d'erreur signalés. Les résultats du sondage ont également fournissent souvent des informations forte, même lorsqu'il n'y a pas une différence statistiquement significative.
Lorsque l'on compare les pourcentages, il peut donc être utile d'envisager la probabilité qu'un pourcentage est plus élevé que l'autre. Dans les situations simples, cette probabilité peut être dérivé avec 1) le calcul de l'erreur-type présenté plus tôt, 2) la formule de la variance de la différence de deux variables aléatoires , et 3) l'hypothèse que si quelqu'un ne choisit pas Kerry ils choisiront Bush , et vice versa; ils sont parfaitement négativement corrélés . Cela peut ne pas être une hypothèse défendable quand il ya plus de deux réponses possibles sondage. Pour plus de conceptions d'enquêtes complexes, différentes formules de calcul de l'erreur-type de la différence doivent être utilisés.
L'erreur type de la différence des pourcentages p et q pour Kerry à Bush, en supposant qu'ils sont parfaitement corrélés négativement, suit:
- Erreur standard de différence =
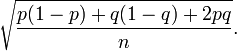
Compte tenu de la différence de pourcentage observé p - q (2% ou 0,02) et l'erreur-type de la différence calculée ci-dessus (0,03), une calculatrice statistique peut être utilisée pour calculer la probabilité qu'un échantillon d'une distribution normale avec moyenne de 0,02 et norme déviation 0,03 est supérieur à 0.
L'application de ces calculs à l'exemple des résultats Newsweek dans une probabilité de 75% que Kerry était «vraiment» de premier plan.