
Elipse
Antecedentes
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?
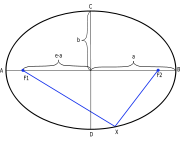

En matemáticas , una elipse (del griego ἔλλειψις, literalmente ausencia) es un locus de puntos en un plano tal que la suma de las distancias a dos puntos fijos es una constante. Los dos puntos fijos se llaman focos (plural de el foco). Una definición alternativa sería que una elipse es la trayectoria trazada por un punto cuya distancia desde un punto fijo, llamado foco, mantiene una relación constante de menos de uno con su distancia desde una línea recta que no pasa por el foco, denominado directriz.
Visión de conjunto
Una elipse es un tipo de sección cónica : si una superficie cónica se corta con un plano que no corta la base del cono, la intersección del cono y el plano es una elipse. Para una prueba elemental por debajo de este, ver Esferas de Dandelin.
Algebraicamente , una elipse es una curva en el plano cartesiano definido por una ecuación de la forma
de tal manera que 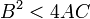 , Donde todos los coeficientes son reales, y donde más de una solución, que define un par de puntos (x, y) de la elipse, existe.
, Donde todos los coeficientes son reales, y donde más de una solución, que define un par de puntos (x, y) de la elipse, existe.
Una elipse se puede dibujar con dos alfileres, un lazo de cuerda y un lápiz. Los pasadores se colocan en los focos y los pasadores y lápiz están encerrados dentro de la cadena. El lápiz se coloca en el papel dentro de la cadena, por lo que la cadena está tensada. La cadena se forma un triángulo . Si el lápiz se mueve alrededor para que la cadena se mantiene tensa, la suma de las distancias desde el lápiz para los pasadores se mantendrá constante, la satisfacción de la definición de una elipse.
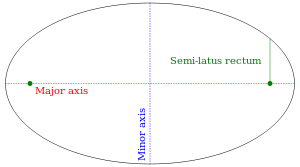
La segmento de línea AB, que pasa a través de los focos y termina en la elipse, se llama el eje mayor. El eje mayor es el segmento más largo que se puede obtener por la unión de dos puntos en la elipse. El CD segmento de línea, que pasa a través del centro (a medio camino entre los focos), perpendicular al eje mayor, y termina en la elipse, se llama el eje menor. La semieje mayor (indicada por A en la figura) es una media del eje mayor: el segmento de línea desde el centro, a través de un enfoque, y al borde de la elipse. Asimismo, el semieje menor (indicada por b en la figura) es una media del eje menor.
Si los dos focos coinciden, entonces la elipse es un círculo ; en otras palabras, un círculo es un caso especial de una elipse, uno donde el excentricidad es cero.
Una elipse centrada en el origen puede ser visto como la imagen de la círculo unidad bajo un mapa lineal asociado con una matriz simétrica 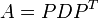 ,
, 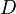 siendo un matriz diagonal con los valores propios de
siendo un matriz diagonal con los valores propios de 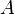 , Ambos de los cuales son real positivo, a lo largo de la diagonal principal, y
, Ambos de los cuales son real positivo, a lo largo de la diagonal principal, y 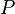 ser un verdadero matriz unitaria que tiene como columnas los vectores propios de
ser un verdadero matriz unitaria que tiene como columnas los vectores propios de 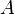 . A continuación, los ejes de la elipse se encuentran a lo largo de los vectores propios de
. A continuación, los ejes de la elipse se encuentran a lo largo de los vectores propios de 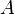 Y la (raíz cuadrada de los valores propios) son las longitudes de los semiejes mayor y menor.
Y la (raíz cuadrada de los valores propios) son las longitudes de los semiejes mayor y menor.
Una elipse puede ser producido por la multiplicación de las coordenadas x de todos los puntos en un círculo por una constante, sin necesidad de cambiar las coordenadas y. Esto es equivalente a estirar el círculo en la dirección x.
Excentricidad
La forma de una elipse puede ser expresada por un número llamado la excentricidad de la elipse, convencionalmente denotado  . La excentricidad es un número no negativo menor que 1 y mayor o igual a 0. Es el valor de la relación constante de la distancia de un punto en una elipse de un enfoque para que a partir de la directriz correspondiente. Una excentricidad de 0 implica que los dos focos ocupan el mismo punto y que la elipse es un círculo .
. La excentricidad es un número no negativo menor que 1 y mayor o igual a 0. Es el valor de la relación constante de la distancia de un punto en una elipse de un enfoque para que a partir de la directriz correspondiente. Una excentricidad de 0 implica que los dos focos ocupan el mismo punto y que la elipse es un círculo .
Para una elipse con semieje mayor ay semieje menor b, la excentricidad es
Cuanto mayor es la excentricidad es, cuanto mayor es el relación de A a B, y por lo tanto la más alargada la elipse.
Si c es igual a la distancia desde el centro a cualquiera de enfoque, entonces
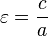 .
.
La distancia c es conocida como la excentricidad lineal de la elipse. La distancia entre los focos es 2 c o 2 aε.
También,
donde  es el excentricidad angular.
es el excentricidad angular.
Ecuaciones
Una elipse con un eje semi-mayor y un semieje menor b, centrada en el punto  y que tiene su eje mayor paralelo a la eje x puede ser especificado por la ecuación
y que tiene su eje mayor paralelo a la eje x puede ser especificado por la ecuación
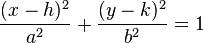 .
.
Esta elipse se puede expresar paramétricamente como
donde 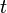 puede ser restringido al intervalo
puede ser restringido al intervalo  .
.
Forma paramétrica de una elipse girada por un ángulo 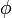 :
:
La fórmula para los directrixes es
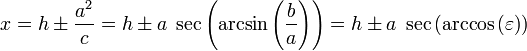 .
.
Si 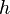 = 0 y
= 0 y 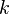 = 0 (es decir, si el centro es el origen (0,0)), entonces podemos expresar esta elipse en coordenadas polares por la ecuación
= 0 (es decir, si el centro es el origen (0,0)), entonces podemos expresar esta elipse en coordenadas polares por la ecuación
donde  es la excentricidad de la elipse.
es la excentricidad de la elipse.
Con un foco en el origen, la ecuación polar de la elipse es
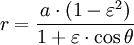 .
.
La Forma de Gauss-asignada:
tiene la normalidad 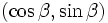 .
.
Recto Semi-latus y coordenadas polares
El recto semi-latus de una elipse, denotado generalmente 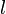 ( minúscula L), es la distancia desde un foco de la elipse a la propia elipse, medida a lo largo de una línea perpendicular al eje mayor. Se relaciona con
( minúscula L), es la distancia desde un foco de la elipse a la propia elipse, medida a lo largo de una línea perpendicular al eje mayor. Se relaciona con  y
y 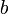 (Semi-ejes de la elipse) por la fórmula
(Semi-ejes de la elipse) por la fórmula 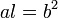 o, si se utiliza la excentricidad,
o, si se utiliza la excentricidad,  .
.
En coordenadas polares , una elipse con un foco en el origen y el otro en el eje x negativo está dada por la ecuación
Una elipse también puede ser pensado como una proyección de un círculo: un círculo en un plano en ángulo φ a la horizontal proyectada verticalmente sobre un plano horizontal da una elipse de φ sin excentricidad, siempre φ no es 90 °.
Área y circunferencia
La área encerrada por una elipse es πab, donde (como antes) a y b son semiejes mayor y menor de la elipse.
La circunferencia 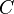 de una elipse es
de una elipse es 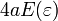 , Donde la función de
, Donde la función de  es la completa integral elíptica de la segunda clase.
es la completa integral elíptica de la segunda clase.
La exacta serie infinita es:
O:
Un buen aproximación es Ramanujan de:
que también puede ser escrito como:
Para el caso especial en el que el eje menor es la mitad del eje mayor, obtenemos:
o 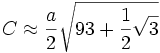 (Mejor aproximación).
(Mejor aproximación).
Más generalmente, el longitud de arco de una porción de la circunferencia, como una función del ángulo subtendido, está dada por una incompleta integral elíptica. La función inversa , el ángulo subtendido como una función de la longitud de arco, está dada por la funciones elípticas.
Estiramiento y proyección
Una elipse puede estirarse uniformemente a lo largo de cualquier eje, en o fuera del plano de la elipse, y todavía será una elipse. La elipse alargada tendrá diferentes propiedades (tal vez cambiada la excentricidad y semi-longitud del eje principal, por ejemplo), pero todavía será una elipse (o una elipse degenerada: un círculo o una línea). Del mismo modo, cualquier proyección oblicua sobre un plano los resultados en una sección cónica. Si la proyección es una curva cerrada en el plano, entonces la curva es una elipse o una elipse degenerada.
Propiedad Reflexión
Asumir una elíptica espejo con una fuente de luz en uno de los focos. Entonces todos los rayos son reflejado a un solo punto - el segundo enfoque. Dado que ninguna otra curva tiene una propiedad tal, puede ser utilizado como una definición alternativa de una elipse. En un círculo, toda la luz se refleja de vuelta al centro ya todas las tangentes son ortogonal a la radio.
Las ondas sonoras se reflejan de manera similar, por lo que en una gran sala elíptica una persona de pie en un foco puede oír una persona de pie en el otro foco notablemente bien. Dicha sala se llama una cámara de susurro. Algunos ejemplos son el Colección Nacional Salón de las Estatuas en el Capitolio de Estados Unidos (donde John Quincy Adams se dice que ha utilizado esta propiedad para espiar en los asuntos políticos), en una exposición en el sonido en el Museo de Ciencia e Industria de Chicago , frente al Universidad de Illinois en Urbana-Champaign Auditorio Foellinger, y también en una cámara lateral del Palacio de Carlos V, en el Alhambra.
Los puntos suspensivos en la física
En el siglo 17 , Johannes Kepler explicó que el órbitas largo de la cual los planetas viajan alrededor del Sol son elipses en su primera ley del movimiento planetario . Más tarde, Isaac Newton explicó esto como un corolario de su la ley de la gravitación universal.
Más en general, en el gravitacional problema de dos cuerpos, si los dos cuerpos están unidos entre sí (es decir, la energía total es negativa), sus órbitas son elipses similares con el común baricentro de ser uno de los focos de cada elipse. El otro foco de la elipse o bien no ha conocido significado físico. Curiosamente, la órbita de cualquiera de cuerpo en el marco de referencia de la otra es también una elipse, con el otro cuerpo en un foco.
La solución general para una oscilador armónico en dos o más dimensiones es también una elipse, pero esta vez con el origen de la fuerza situado en el centro de la elipse.
En la óptica, una elipsoide índice describe el índice de refracción de un material como una función de la dirección a través de ese material. Esto sólo se aplica a materiales que son ópticamente anisotrópica. Véase también birrefringencia.
Los puntos suspensivos en la infografía
Dibujo de una elipse como una gráficos primitivos es común en las bibliotecas de presentación estándar, tales como el Macintosh API QuickDraw, Windows Interfaz de dispositivo gráfico (GDI) y la Windows Presentation Foundation (WPF). A menudo, estas bibliotecas son limitados y sólo pueden dibujar una elipse, ya sea con el eje mayor o la horizontal eje menor. Jack Bresenham en IBM es el más famoso por la invención de primitivas de dibujo en 2D, incluyendo líneas y dibujo de círculo, usando operaciones con enteros sólo rápidas como la suma y la rama de bit de acarreo. Una generalización eficiente para dibujar elipses fue inventado en 1984 por Jerry Van Aken (IEEE CG & A, septiembre 1984).
La siguiente es ejemplo de código JavaScript utilizando la fórmula paramétrico para una elipse para calcular un conjunto de puntos. La elipse puede entonces aproximarse mediante la conexión de los puntos con líneas.
/ ** * Esta función devuelve una matriz que contiene 36 puntos para dibujar una elipse *. * *param X {} doble coordenada X *param y {} doble coordenada *param un doble {} semieje *param b {} doble semieje menor ángulo * @ Param {} doble ángulo de la elipse */ function calculateEllipse ( x , y , a , b , angle , steps ) { if ( steps == null ) steps = 36 ; var points = [ ] ; var beta = - angle / 180 * Math . PI ; var sinbeta = Math . sin ( beta ) ; var cosbeta = Math . cos ( beta ) ; for ( var i = 0 ; i < 360 ; i += 360 / steps ) { var alpha = i / 180 * Math . PI ; var sinalpha = Math . sin ( alpha ) ; var cosalpha = Math . cos ( alpha ) ; var X = x + ( a * cosalpha * cosbeta - b * sinalpha * sinbeta ) ; var Y = y + ( a * cosalpha * sinbeta + b * sinalpha * cosbeta ) ; points. push ( new OpenLayers. Geometry . Point ( X , Y ) ) ; } return points ; }
Una consecuencia beneficiosa del uso de la fórmula paramétrica es que la densidad de puntos es mayor donde no es la más curvatura. Por lo tanto, el cambio en la pendiente entre cada punto sucesivo es pequeño, la reducción de la "jagginess" aparente de la aproximación.

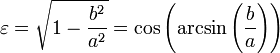
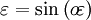
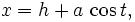
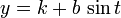
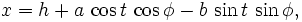
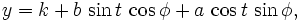
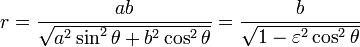

![C = 2 \ pi a \ left [{1 - \ left ({1 \ over 2} \ right) ^ 2 \ varepsilon ^ 2 - \ left ({1 \ cdot 3 \ over 2 \ cdot 4} \ right) ^ 2 {\ varepsilon ^ 4 \ over 3} - \ left ({1 \ cdot 3 \ cdot 5 \ over 2 \ cdot 4 \ cdot 6} \ right) ^ 2 {\ varepsilon ^ 6 \ over5} - \ dots} \ right] \! \,](../../images/93/9311.png)
![C = 2 \ pi a \ sum_ {n = 0} ^ \ infty {\ left \ lbrace - \ left [\ prod_ {m = 1} ^ n \ left ({2m-1 \ más de 2 m} \ right) \ right ] ^ 2 {\ varepsilon ^ {2n} \ sobre 2n - 1} \ right \} rbrace](../../images/93/9312.png)
![C \ aprox \ pi \ left [3 (a + b) - \ sqrt {(3a + b) (a + 3b)} \ right]! \ \,](../../images/93/9313.png)
![C \ aprox \ pi a \ left [3 (1 + \ sqrt {1- \ varepsilon ^ 2}) - \ sqrt {(3 + \ sqrt {1- \ varepsilon ^ 2}) (1 + 3 \ sqrt {1 - \ varepsilon ^ 2})} \ right] \ \,](../../images/93/9314.png)

