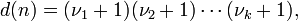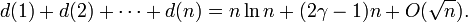Diviseur
Contexte des écoles Wikipédia
Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?
En mathématiques , un diviseur d'un nombre entier n, aussi appelé un facteur de n, est un nombre entier qui divise uniformément sans laisser de n reste.
Explication
Par exemple, la figure 7 est un diviseur de 42 parce 42/7 = 6. On dit également 42 est divisible par 7 ou 42 est une multiple de 7 ou 7 ou 42 divise 7 est un facteur de 42 et on écrit habituellement 7 | 42. Par exemple, les diviseurs positifs de 42 sont 1, 2, 3, 6, 7, 14, 21, 42.
En général, nous disons m | n (lire: m divise n) pour des entiers non nuls m et n ssi il existe un entier k tel que n = km. Ainsi, diviseurs peuvent être négatifs aussi bien que positifs, bien souvent, nous limitons notre attention aux diviseurs positifs. (Par exemple, il ya six diviseurs de quatre, 1, 2, 4, -1, -2, -4, mais seraient habituellement ne citer que les aspects positifs, 1, 2 et 4.)
1 et -1 fracture (sont diviseurs de) tout entier, tout entier (et sa négation) est un diviseur de lui-même, et tout entier est un diviseur de 0, sauf par convention 0 lui-même (voir aussi division par zéro). Nombres divisibles par 2 sont appelés même et les numéros non divisible par 2 sont appelés impair.
Un diviseur de n qui ne est pas 1, -1, n ou - n (qui sont des diviseurs triviaux) est connu comme un diviseur non négligeable; numéros avec diviseurs non triviaux sont connus comme nombres composés, tout en nombres premiers ne ont pas de diviseurs non triviaux.
Le nom vient de l' arithmétique fonctionnement de la division : si un / b = c alors un est le dividende , le diviseur b, et c la quotient.
Il y a propriétés qui permettent de reconnaître certains diviseurs d'un nombre compris entre les chiffres de ce numéro.
D'autres notions et des faits
 | Le Wikibook Le Livre de preuves mathématiques a une page sur le thème de: Les preuves de propriétés de divisibilité |
Quelques règles élémentaires:
- Si a | b et a | c, alors a | (b + c), en effet, a | (mb + nc) pour tous les entiers m, n.
- Si a | b et b | c, alors a | c. ( transitive relation)
- Si a | b et b | a, alors a = b ou a = - b.
La propriété suivante est important:
- Si a | bc et pgcd (a, b) = 1, puis a | c. ( D'Euclide lemme)
Un diviseur positif de n qui est différent de n est appelé un diviseur approprié (ou partie aliquote) de n. (Un nombre qui ne divise pas uniformément n, mais laisse un reste, est appelé un cadre aliquant de n.)
Un entier n> 1 dont le seul dénominateur est une bonne est appelé un nombre premier . Équivalente, on dirait que un nombre premier est celui qui a exactement deux facteurs: 1 et lui-même.
Toute diviseur positif de n est un produit de diviseurs premiers de n soulevé une certaine puissance. Ce est une conséquence du théorème fondamental de l'arithmétique .
Si un nombre égal à la somme de ses diviseurs propres, il est dit d'être un nombre parfait . Les nombres inférieurs à la somme de leurs diviseurs propres sont dits abondante; tandis que les nombres supérieurs à cette somme sont dits déficient.
Le nombre de diviseurs positifs de n est un fonction multiplicative d (n) (par exemple D (42) = 8 = 2 × 2 × 2 = d (2) × d (3) x d (7)). La somme des diviseurs positifs de n est une autre fonction multiplicative σ (n) (par exemple, σ (42) = 96 = 3 x 4 x 8 = σ (2) x σ (3) x σ (7)). Ces deux fonctions sont des exemples de fonctions de diviseur.
Si le Premier factorisation de n est donnée par
puis le nombre de diviseurs positifs de n est
et chacun des diviseurs est de la forme
où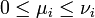 
pour chaque 
.
On peut montrer que
Une interprétation de ce résultat est que un nombre entier positif choisi de manière aléatoire un nombre n a prévu des diviseurs d'environ 
.
Divisibilité des nombres
La relation de divisibilité tourne l'ensemble N des non-négatifs entiers dans un partiellement ordonné ensemble, en fait, dans un compléter treillis distributif. L'élément le plus important de ce réseau est égal à 0 et le plus petit est égal à 1. Le fonctionnement de la compétition ^ est donné par le plus grand commun diviseur et le fonctionnement de la jointure v moins commun multiple. Ce réseau est isomorphe au double de la réseau de sous-groupes de l'infini groupe cyclique Z .
Généralisation
On peut parler de la notion de divisibilité en tout intègre. Se il vous plaît voir cet article pour les définitions dans ce réglage.
