
Nombre négatif
Renseignements généraux
Enfants SOS offrent un chargement complet de la sélection pour les écoles pour une utilisation sur les intranets des écoles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...
Un nombre négatif est un nombre qui est inférieure à zéro , tel que -3. Un nombre positif est un nombre qui est supérieur à zéro, comme 3. Zéro soi ne est ni positif ni négatif. Les numéros non-négatifs sont les nombres réels qui ne sont pas négative (ils sont positif ou nul). Les numéros non-positifs sont les nombres réels qui ne sont pas positif (elles sont négatives ou nulles).
Dans le contexte de nombres complexes , positif implique réel, mais pour plus de clarté, on peut dire «nombre réel positif".
Les nombres négatifs
Les entiers négatifs peuvent être considérés comme une extension des nombres naturels , tels que l'équation x - y = z a une solution valable pour toutes les valeurs de x et y. Les autres séries de chiffres sont ensuite dérivés comme des extensions de plus en plus élaborés et des généralisations à partir des nombres entiers.
Les nombres négatifs sont utiles pour décrire les valeurs sur une échelle qui va au-dessous de zéro, tels que la température , et aussi dans comptabilité où ils peuvent être utilisés pour représenter dettes. En comptabilité, les dettes sont souvent représentés par chiffres rouges, ou un nombre entre parenthèses.
Numéros non-négatifs
Un nombre est non négatif si et seulement si elle est supérieure ou égale à zéro , à savoir, positive ou nulle. Ainsi, les entiers naturels sont tous les entiers de zéro sur le haut, et les réels positifs sont tous les nombres réels de zéro sur le haut.
Un véritable matrice A est appelé non négatif si chaque entrée de A est positive.
Un véritable matrice A est appelé totalement non négative par les théoriciens de la matrice ou totalement positif par des informaticiens si le facteur déterminant de chaque sous-matrice carrée de A est positive.
Le négatif d'un nombre unique
Le négatif d'un numéro est unique, comme le montre la preuve suivante.
La preuve en est par la contradiction.
Soit X un numéro et laissez -x être son négatif. Laisser 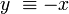 . Laisser
. Laisser  être un autre négatif de x. Ensuite, il doit être vrai que
être un autre négatif de x. Ensuite, il doit être vrai que  . Par un axiome du système des nombres réels
. Par un axiome du système des nombres réels
 ,
,  .
.
Et donc, 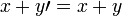 . En utilisant la loi d'annulation pour l'addition, on voit que
. En utilisant la loi d'annulation pour l'addition, on voit que 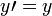 , Ce qui contredit notre supposition. Donc
, Ce qui contredit notre supposition. Donc  est le même nombre que
est le même nombre que  et est le négatif unique de x.
et est le négatif unique de x.
Fonction Signum
Il est possible de définir une fonction sgn (x) sur les nombres réels qui est une pour les nombres positifs, -1 pour les nombres négatifs et 0 pour zéro (parfois appelé le fonction signum):
Nous avons alors (sauf pour x = 0):
Où | x | est la valeur absolue de x et H (x) est la Fonction de Heaviside. Voir aussi dérivé .
Fonction complexe Signum
Il est possible de définir une fonction CSGN (x) sur les nombres complexes ce qui est une des nombres positifs, pour les nombres négatifs -1 et 0 pour zéro (parfois appelé le fonction signe complexe):
Lorsque le complexe inégalités doit être interprétée comme suit
Nous avons alors (sauf pour x = 0):
Arithmétique impliquant des nombres signés
Addition et soustraction
Aux fins de l'addition et la soustraction, on peut penser que des nombres négatifs dettes.
Ajout d'un nombre négatif est le même que soustrayant le nombre positif correspondant:
- + 5 (-3) = 5-3 = 2
- (Si vous avez 5 $ et l'acquisition d'une dette de $ 3, alors vous avez une valeur nette de $ 2)
- -2 + (-5) = -2 À 5 = -7
(Afin d'éviter toute confusion entre les concepts de la soustraction et la négation, souvent le signe négatif est écrit en exposant:
- - 2 + - = 5 - 2 - 5 = - 7)
Soustrayant un nombre positif d'un nombre positif plus petit donne un résultat négatif:
- 4-6 = -2
- (Si vous avez 4 $ et dépenser 6 $, alors vous avez une dette de 2 $).
Soustrayant un nombre positif de tout nombre négatif donne un résultat négatif:
- -3-6 = -9
- (Si vous avez une dette de 3 $ et de passer une autre 6 $, vous avez une dette de 9 $).
Soustrayant un négatif est équivalent à l'ajout positif correspondant:
- 5 - (-2) = 5 + 2 = 7
- (Si vous avez une valeur nette de $ 5 et vous débarrasser d'une dette de 2 $, alors votre nouvelle valeur nette est de 7 $).
Également:
- -8 - (-3) = -5
- (Si vous avez une dette de 8 $ et de se débarrasser d'une dette de 3 $, alors vous avez encore une dette de $ 5).
Multiplication
Brahmagupta indiqué dans Brahmasputhasiddhanta "temps positifs positif est fois positifs et négatifs négative est positif". Cette notion a été contestée par Lazare Carnot (1753-1823). Il a demandé comment la place d'un petit nombre pourrait être plus grand que la place d'un grand nombre. En d'autres termes carré de -3 est plus grand que le carré de 2. Pourtant, -3 est inférieure à 2. Cette objection de Carnot à la notion de Brahmagupta était pas contestée pendant un siècle. Grands mathématiciens tels que Euler, Laplace et Cauchy ont été incapables de fournir une réponse complète. Hermann Hankel prouvé en utilisant des nombres complexes qui Brahmagupta avait raison. . (Référence Intuition en sciences et en mathématiques, Efrain Fischbein, Kluwer Academic Publishers, Springer, 1899) Multiplication d'un nombre négatif par un nombre positif donne un résultat négatif: -2 × 3 = -6. Multiplication de deux nombres négatifs donne un résultat positif: -4 × -3 = 12.
Une façon de comprendre ce est de considérer la multiplication par un nombre positif que l'addition répétée. Pensez à 3 x 2 que trois groupes, deux dans chaque groupe. Ainsi, 3 x 2 = 2 + 2 + 2 = 6 si naturellement et -2 × 3 = (-2) + (-2) + (-2) = -6.
Multiplication par un nombre négatif peut être considéré comme une addition répétée ainsi. Par exemple, 3 × -2 peut être considéré comme trois groupes, avec -2 dans chaque groupe. 3 × -2 = (-2) + (-2) + (-2) = -6. Notez que cela empêche la multiplication commutative : 3 × -2 = -2 × 3 = -6.
En appliquant la même interprétation du terme "multiplication par un nombre négatif" pour une valeur qui est également négatif, on a:
| -4 -3 × | = - (-4) - (-4) - (-4) |
| = 4 + 4 + 4 | |
| = 12 |
Cependant, d'un point de vue formel, la multiplication de deux nombres négatifs est reçu directement par l'intermédiaire du distributivité de la multiplication sur l'addition:
| -1 -1 × | |
| = (-1) X (-1) + (-2) + 2 | |
| = (-1) X (-1) + (-1) × 2 + 2 | |
| = (-1) X (1 + 2) + 2 | |
| = (-1) X 1 + 2 | |
| = (-1) + 2 | |
| = 1 |
Division
Division est similaire à la multiplication. Brahmagupta a déclaré pour la première fois ce négatif divisé par négatif au positif. Positif divisé par négative à être négatif. (Référence: Arithmétique et mensuration de Brahmagupta par Colebrooke HT). La convention de Brahmagupta a survécu à ce jour: si la dividende et diviseur ont des signes différents, alors le résultat est négatif.
- 8 / = -2 -4
- -10 / 2 = -5
Si dividende et le diviseur ont le même signe, le résultat est positif, même si les deux sont négatifs.
- -12 / -3 = 4
Construction formelle de nombres entiers négatifs et non-négatifs
D'une manière similaire à des nombres rationnels , on peut étendre le nombre naturel N jusqu'au entiers Z en définissant en tant que nombres entiers paire ordonnée de nombres naturels (a, b). Nous pouvons étendre addition et la multiplication de ces paires avec les règles suivantes:
- (A, b) + (c, d) = (a + c, b + d)
- (A, b) x (C, D) = (a × b + c × d, d + a × b × c)
Nous définissons une relation d'équivalence ~ sur ces paires avec la règle suivante:
- (A, b) ~ (c, d) si et seulement si A + D = b + c.
Cette relation d'équivalence est compatible avec l'addition et la multiplication défini ci-dessus, et l'on peut définir comme la Z quotient fixé N ² / ~, ce est à dire nous identifions deux paires (a, b) et (c, d) si elles sont équivalentes au sens ci-dessus.
Nous pouvons également définir une ordre total sur Z par écrit
- (A, b) ≤ (c, d) si et seulement si a + d ≤ b + c.
Cela conduira à un additif zéro de la forme (a, a), un inverse additif de (a, b) de la forme (b, a), une unité de multiplication de la forme (a + 1, a), et un définition de soustraction
- (A, b) - (c, d) = (a + d, b + c).
Première utilisation de nombres négatifs
Pendant longtemps, les solutions aux problèmes négatifs ont été considérés comme "false" parce qu'ils ne pouvaient être trouvés dans le monde réel (dans le sens où on ne peut pas, par exemple, avoir un nombre négatif de graines). Le concept abstrait a été reconnu dès 100 BC - 50 BC A Travail chinois, Neuf chapitres sur l'art mathématique (Jiu-zhang suanshu), contient des méthodes pour trouver les zones de chiffres; rouge tiges de comptage ont été utilisés pour désigner positif coefficients, tiges noires pour le négatif. Les Chinois ont également pu résoudre des équations simultanées impliquant des nombres négatifs. L'ancienne indienne Bakhshali Manuscrit, qui a été écrit à un moment donné entre 200 avant JC et AD 300, effectué des calculs avec des nombres négatifs, en utilisant "+" comme un signe négatif. Ce sont les premières utilisations connues de nombres négatifs.
En Egypte hellénistique, Diophante dans le troisième siècle de notre ère appelée une équation qui était équivalente à 4 x + 20 = 0 (qui a une solution négative) Arithmetica, disant que l'équation était absurde. Cela indique que pas de notion de nombres négatifs existait dans le Méditerranée antique.
Pendant le VIIe siècle après JC, les nombres négatifs ont été utilisés dans l'Inde pour représenter dettes. Le mathématicien indien Brahmagupta , dans Brahma-Sphuta-Siddhanta (écrit en AD 628), discuté de l'utilisation des nombres négatifs pour produire la forme générale formule quadratique qui reste en usage aujourd'hui. Il a également trouvé des solutions négatifs des équations du second degré et a donné des règles concernant les opérations portant sur des nombres négatifs et zéro , comme "Une dette coupé du néant devient un crédit;. un crédit coupée du néant devient une dette" Il a appelé nombres positifs "fortunes, "zéro" un chiffre ", et les nombres négatifs" de dettes. "
Pendant le huitième siècle de notre ère, le Monde islamique appris nombres négatifs de l'arabe traductions des œuvres de Brahmagupta, et en AD 1000 mathématiciens arabes étaient utiliser des nombres négatifs pour les dettes.
Dans le XII e siècle en Inde, Bhaskara également donné racines négatives pour équations du second degré, mais les a rejetées parce qu'elles étaient inappropriées dans le contexte du problème. Il a déclaré que une valeur négative est "dans ce cas de ne pas être pris, car il est insuffisant, les gens ne approuvent pas de racines négatives."
La connaissance des nombres négatifs finalement atteint l'Europe à travers latine traductions de l'arabe et des œuvres indiennes.
Européennes mathématiciens, pour la plupart, ont résisté à la notion de nombres négatifs jusqu'à ce que le 17ème siècle , bien que Fibonacci permis solutions négatives dans les problèmes financiers où ils pourraient être interprétés comme des débits (chapitre 13 Liber Abaci, AD 1202) et plus tard comme des pertes (en Flos). A cette époque, les chinois ont été indiquant les nombres négatifs en dessinant un trait diagonal à travers le plus à droite non nulle chiffres.
Au 15ème siècle, Nicolas Chuquet, un Français, utilisé comme nombres négatifs exposants et appelaient les "numéros absurdes."
En AD 1759, Francis Maseres, un mathématicien anglais, a écrit que les nombres négatifs "assombrissent les doctrines très entiers des équations et faire sombre des choses qui sont dans leur nature trop évident et simple". Il est venu à la conclusion qu'il ne existait nombres négatifs.
Les nombres négatifs ne ont pas été bien compris jusqu'à l'époque moderne. Aussi récemment que le 18ème siècle , le Swiss mathématicien Leonhard Euler croit que les nombres négatifs étaient supérieures à l'infini , un point de vue qui a été partagé par John Wallis. Ce était une pratique courante à l'époque d'ignorer les résultats négatifs dérivés à partir des équations, dans l'hypothèse où ils ne ont aucun sens. ( remaniée de 4) L'argument selon lequel les nombres négatifs sont supérieurs à l'infini impliqué le quotient 1 / x et compte tenu de ce qui se passe quand x tend et traverse le point x = 0 du côté positif.





