Fractal

L' ensemble de Mandelbrot est un exemple célèbre d'une fractale.

Une vue rapprochée de l'ensemble de Mandelbrot.

Une fractale est généralement «une rugueuse ou fragmenté forme géométrique qui peut être subdivisé en plusieurs parties, dont chacune est (au moins approximativement) une copie de taille réduite de l'ensemble, «une propriété appelée auto-similarité. Le terme a été inventé par Benoît Mandelbrot en 1975 et a été dérivé du latin fractus sens "cassé" ou "fracturé".

Une fractale a souvent les caractéristiques suivantes:

• Il a une structure fine au arbitrairement petites échelles.
• Il est trop irrégulière pour être facilement décrit dans traditionnelle géométrique euclidien langue.
• C'est auto-similaire (au moins approximativement ou de manière stochastique).
• Il a un Hausdorff dimension qui est supérieure à sa dimension topologique (bien que cette exigence ne est pas satisfaite par courbes de remplissage d'espace comme le Courbe de Hilbert).
• Il a un simple et définition récursive.

Parce qu'ils semblent similaires à tous les niveaux de grossissement, fractales sont souvent considérées comme infiniment complexe (en termes informels). Les objets naturels que les fractales approximatives à un degré comprennent nuages, chaînes de montagnes, des éclairs, des côtes et des flocons de neige. Cependant, tous les objets auto-similaires sont fractales, par exemple, le ligne réelle (une ligne droite Ligne euclidienne) est formellement auto-similaire, mais ne parvient pas à avoir d'autres caractéristiques fractales.

Histoire

Pour créer un Koch flocon de neige, commencer avec un triangle équilatéral et remplacer le troisième milieu de chaque segment de ligne avec une paire de segments de lignes qui forment un équilatéral "bosse." Puis effectuer la même remplacement sur chaque segment de ligne de la forme obtenue, ad infinitum. Avec chaque itération, le périmètre de cette forme augmente de 1/3. Le flocon de Koch est le résultat d'un nombre infini de ces itérations, et a une longueur infinie, tandis que sa surface reste fini. Pour cette raison, les flocons de neige et de constructions similaires Koch étaient parfois appelés «courbes de monstre."

Les mathématiques derrière fractales ont commencé à prendre forme dans le 17ème siècle, quand le philosophe Leibniz considéré auto-similarité récursif (même se il a fait l'erreur de penser que seule la ligne droite était auto-similaire en ce sens).

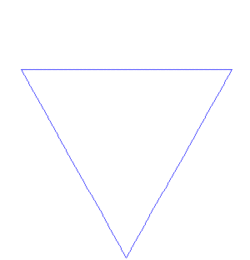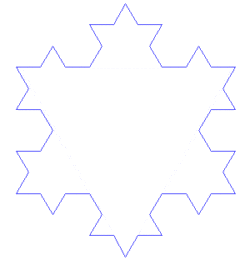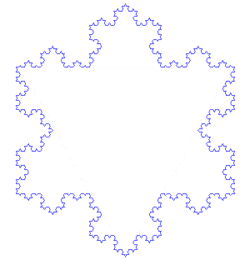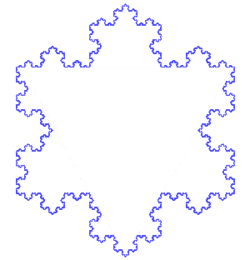
Il a fallu attendre 1872 avant qu'une fonction est apparue dont graphe aujourd'hui serait considéré fractale, lorsque Karl Weierstrass a donné une exemple d'une fonction de la non- propriété intuitive d'être partout mais continu nulle part différentiables. En 1904, Helge von Koch, mécontent avec une définition très abstraite et analytique de Weierstrass, a donné une définition plus géométrique d'une fonction similaire, qui est maintenant appelé le Flocon de Koch. En 1915, Waclaw Sierpinski a construit son triangle et, un an plus tard, son tapis. Initialement ces fractales géométriques ont été décrits comme des courbes plutôt que les formes 2D qu'ils sont connus que dans leurs constructions modernes. L'idée de courbes auto-similaire a été prise plus loin en Paul Pierre Lévy, qui, dans ses 1938 Paper Plane ou l'espace courbes et des surfaces composées de parties similaires au Tout décrit une nouvelle courbe fractale, le Courbe de Lévy.

Georg Cantor a également donné des exemples de sous-ensembles de la ligne réelle avec inhabituels propriétés-ci Ensembles de Cantor sont désormais reconnus comme des fractales.

Fonctions itérés dans le plan complexe ont été étudiés à la fin du 19ème et début du 20ème siècles par Henri Poincaré, Felix Klein, Pierre Fatou et Gaston Julia. Toutefois, sans l'aide de l'infographie modernes, ils ne avaient pas les moyens de visualiser la beauté de la plupart des objets qu'ils avaient découverts.

Dans les années 1960, Benoît Mandelbrot a commencé à enquêter auto-similarité dans des documents tels que Quelle est la durée de la côte de la Bretagne? Statistique d'auto-similarité et fractionnaire Dimension, qui se appuie sur des travaux antérieurs de Lewis Fry Richardson. Enfin, en 1975 Mandelbrot a inventé le mot «fractal» pour désigner un objet dont Dimension de Hausdorff-Besicovitch est supérieure à sa dimension topologique. Il a illustré cette définition mathématique frappant visualisations construit par ordinateur. Ces images capturées l'imagination populaire; beaucoup d'entre eux étaient basés sur la récursivité, conduisant à sens populaire du terme «fractal».

Exemples

Un Ensemble de Julia, une fractale lié à l'ensemble de Mandelbrot

Une classe relativement simple d'exemples est donnée par la Cantor définit, Triangle de Sierpinski et tapis, Éponge de Menger, courbe dragon, courbe de remplissage d'espace, et Courbe de Koch. D'autres exemples de fractales sont les Lyapunov fractale et les ensembles de limites de Groupes kleiniens. Fractales peuvent être déterministe (tout ce qui précède) ou stochastique (ce est-à non-déterministe). Par exemple, les trajectoires du Mouvement brownien dans le plan ont une dimension de Hausdorff de deux.

Systèmes dynamiques chaotiques sont parfois associés à des fractales. Objets dans la l'espace de phase d'un système dynamique peut être fractales (voir attracteur). Objets dans la espace des paramètres pour une famille de systèmes peut être fractale ainsi. Un exemple intéressant est l' ensemble de Mandelbrot . Cet ensemble contient des disques entiers, il a donc une dimension Hausdorff égale à sa dimension topologique de deux, mais ce qui est vraiment surprenant, ce est que le limite de l'ensemble de Mandelbrot a également une dimension de Hausdorff de deux (alors que la dimension topologique de 1), un résultat prouvé par Mitsuhiro Shishikura en 1991. Une fractale étroitement liée est le Ensemble de Julia.

Même courbes lisses simples peuvent exposer les biens fractale de l'auto-similarité. Par exemple, le courbe en loi de puissance (aussi connu comme un Distribution de Pareto) produit des formes similaires à différents grossissements.

fractales Génération

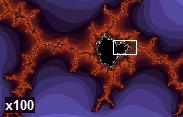Même 2000 fois grossissement de l'ensemble de Mandelbrot découvre des détails fins ressemblant à l'ensemble.

Trois techniques communes pour générer des fractales sont:

• Fractales évasion-temps - Elles sont définies par un récurrence rapport à chaque point dans un espace (tel que le plan complexe ). Des exemples de ce type sont l' ensemble de Mandelbrot , Ensemble de Julia, le Brûler fractale de navire et la Fractale de Lyapunov.
• Systèmes de fonctions itérées - Celles-ci ont une règle de remplacement géométrique fixe. Ensemble de Cantor, Tapis de Sierpinski, Triangle de Sierpinski, Courbe de Peano, Koch flocon de neige, Harter-Heighway courbe de dragon, T-Square, Éponge de Menger, sont quelques exemples de ces fractales.
• Fractales aléatoires - générés par des processus stochastiques plutôt que déterministes, par exemple, les trajectoires de la Mouvement brownien, Lévy vol, paysages fractales et la Arbre brownien. Ce dernier rendements dits mass-fractales ou dendritiques, par exemple, agrégation limitée par diffusion ou grappes d'agrégation réaction limitée.

Classification

Fractales peuvent également être classés en fonction de leur auto-similarité. Il ya trois types d'auto-similarité trouvé dans fractales:

• Exact auto-similarité - Ce est le type le plus fort de l'auto-similarité; la fractale semble identique à différentes échelles. Fractales défini par systèmes de fonctions itérées affichent souvent exacte auto-similarité.
• Quasi-auto-similarité - Ce est une forme libre de l'auto-similarité; la fractale apparaît environ (mais pas exactement) identiques à différentes échelles. Fractales quasi auto-similaires contiennent de petites copies de l'ensemble de fractale dans des formes déviantes et dégénérés. Fractales défini par relations récurrence sont généralement quasi-auto-similaire mais pas exactement auto-similaire.
• Statistique auto-similarité - Ce est le type le plus faible de l'auto-similarité; la fractale a des mesures numériques ou statistiques qui sont conservés à travers les échelles. La plupart des définitions raisonnables de "fractale" impliquent trivialement une certaine forme de statistiques auto-similarité. (La dimension fractale se est une mesure numérique qui est conservé à travers les échelles.) Fractales aléatoires sont des exemples de fractales qui sont statistiquement auto-similaire, mais ni exactement ni quasi auto-similaire.

Dans la nature

Une fractale que les modèles de la surface d'une montagne (animation)

Fractales approximatives sont faciles à trouver dans la nature. Ces objets se affichent structure auto-similaire sur une étendue, mais finie, plage d'échelle. Les exemples incluent les nuages, flocons de neige , cristaux , chaînes de montagnes , la foudre, les réseaux fluviaux , chou-fleur ou brocoli, et les systèmes de les vaisseaux sanguins et vaisseaux pulmonaires. Les côtes peuvent être considérées vaguement fractale dans la nature.

Une fougère fractale calculée en utilisant une Système de fonctions itérées

Les arbres et les fougères sont fractale dans la nature et peuvent être modélisés sur un ordinateur en utilisant une récursif algorithme . Cette nature récursive est évident dans ces exemples - une branche d'un arbre ou d'un fronde d'une fougère est une réplique miniature de l'ensemble: pas identiques, mais similaires dans la nature.

En 1999, certains auto formes fractales similaires ont été montré pour avoir une propriété de "l'invariance de fréquence" - les mêmes propriétés électromagnétiques quelle que soit la fréquence - de les équations de Maxwell (voir antenne fractale).

Fractal pentagramme dessiné avec un vecteur programme d'itération

Dans les œuvres de création

Motifs fractals ont été trouvés dans les peintures de l'artiste américain Jackson Pollock . Alors que les peintures de Pollock semblent être composé de gouttes chaotique et les éclaboussures, analyse informatique a trouvé motifs fractals dans son travail.

Décalcomanie, une technique utilisée par des artistes tels que Max Ernst, peut produire des modèles de type fractal. Il se agit en appuyant sur la peinture entre deux surfaces et les écartant.

Les fractales sont également répandu dans L'art africain et de l'architecture. Maisons circulaires apparaissent dans les cercles de cercles, maisons rectangulaires dans des rectangles de rectangles, et ainsi de suite. Ces modèles d'échelle peuvent également être trouvés dans les textiles africains, sculpture, et même des coiffures cornrow.

• 

  Une fractale est formée en tirant en dehors colle à deux-couverts feuilles d'acrylique.

• 

  Ventilation haute tension dans un «bloc acrylique 4 crée une fractale Figure Lichtenberg.

• 

  Ramification de fractale se produit dans une surface fracturée comme un micro-ondes irradiées DVD

• 

  Brocoli Romanesco montrant fractales naturelles très fines

• 

  Un Amas de DLA cultivé à partir d'un cuivre (II) sulfate solution dans un Cellule d'électrodéposition

• 

  A quelques kV sont mis entre deux clous dans certains pins humide. Un soi-disant "fractales" Woodburn résultats.

• 

  Un grossissement de l'ensemble de phoenix

• 

  Pascal fractal

• 

  Un flamme de fractale créée avec le programme Apophysis

Applications

Comme décrit ci-dessus, fractales aléatoires peuvent être utilisés pour décrire de nombreux objets du monde réel très irrégulières. D'autres applications de fractales comprennent:

• Classification des diapositives histopathologiques dans la médecine
• Terrain fractal ou la complexité de Littoral
• Enzyme / enzymologie ( Cinétique de Michaelis-Menten)
• Génération de la nouvelle musique
• Génération de divers art formes
• Signal et compression d'image
• Sismologie
• Fractal en mécanique des sols
• Ordinateur et la conception de jeux vidéo, en particulier infographie pour organiques environnements et dans le cadre de génération procédurale
• Fractographie et mécanique de la rupture
• Antennes fractales - antennes de petite taille en utilisant des formes fractales
• Petite théorie de la diffusion de l'angle des systèmes fractale rugueuses
• Néo-hippies t-shirts et d'autres la mode
• Génération du tracé de camouflage, comme MARPAT
• Cadran numérique
• Prix génération de Série
• La démocratie Fractal