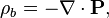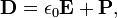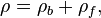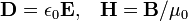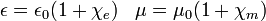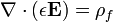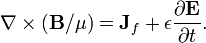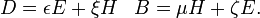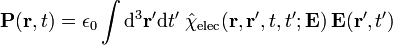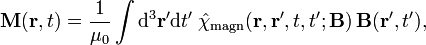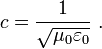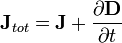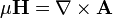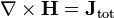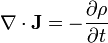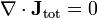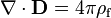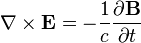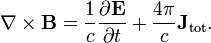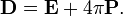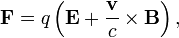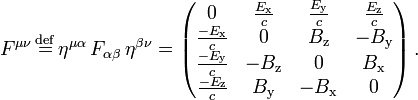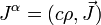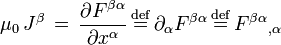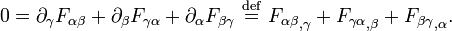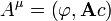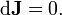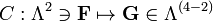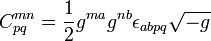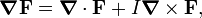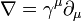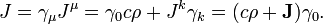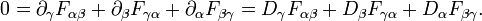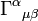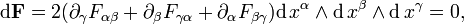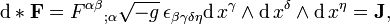Les équations de Maxwell

Sujets connexes: l'électricité et de l'électronique

Contexte des écoles Wikipédia

Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

Electromagnétisme

Électricité Magnétisme
Électrostatique Charge électrique Électricité statique Champ électrique Conducteur Isolant Triboélectricité Décharge électrostatique Induction La loi de Coulomb La loi de Gauss Flux électrique / énergie potentielle Moment dipolaire électrique Polarisation
Magnétostatique La loi d'Ampère Champ magnétique Magnétisation Flux magnétique Loi de Biot-Savart Moment de dipôle magnétique La loi de Gauss à magnétisme
Électrodynamique Droit de la force de Lorentz Induction électromagnétique La loi de Faraday La loi de Lenz Déplacement actuel Les équations de Maxwell Champ électromagnétique Un rayonnement électromagnétique Tenseur de Maxwell Vecteur de Poynting Potentiel Liénard-Wiechert Les équations de Jefimenko À courant de Foucault
Réseau électrique Courant électrique Potentiel électrique Tension Résistance La loi d'Ohm circuit de la série Circuit parallèle Courant continu Courant alternatif Force électromotrice Capacitance Inductance Impédance Cavités résonnantes Guides d'ondes
Formulation covariante Tenseur électromagnétique ( tenseur-énergie) Four à courant continu Potentiel électromagnétique à quatre
Les scientifiques Ampère Coulomb Faraday Gauss Heaviside Henri Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

Les équations de Maxwell sont un ensemble de quatre équations différentielles partielles qui, conjointement avec le Droit de la force de Lorentz, forment le fondement de électrodynamique classique, classiques optique , et les circuits électriques. Ce à son tour sous-tendent la présente radioactivité, télévision-, téléphone-, et d'information-technologies.

Les équations de Maxwell ont deux variantes principales. L'ensemble «microscopique» des équations de Maxwell utilise charge totale et le courant total, y compris les frais de niveau atomique difficiles à calculer et les courants dans les matériaux. L'ensemble «macroscopique» des équations de Maxwell définit deux nouveaux champs auxiliaires qui peuvent contourner avoir à connaître ces charges et des courants de taille «atomique».

Les équations de Maxwell sont nommés d'après le physicien et mathématicien écossais James Clerk Maxwell , car ils se trouvent tous dans un document en quatre parties, Sur les lignes de la force physique, qu'il publia entre 1861 et 1862. La forme mathématique de la loi de la force de Lorentz est également apparu dans le présent document.

Il est souvent utile d'écrire les équations de Maxwell sous d'autres formes qui sont souvent appelés les équations de Maxwell ainsi. Une formulation relativiste en termes de tenseurs covariants sur le terrain est utilisé dans la relativité restreinte. Alors que, en mécanique quantique, une version basée sur le électrique et des potentiels magnétiques est préféré.

Description conceptuelle

Conceptuellement, les équations de Maxwell décrivent comment charges électriques et courants électriques agissent comme sources pour les champs électriques et magnétiques. En outre, on décrit comment un champ électrique variable dans le temps engendre un champ magnétique variant dans le temps et vice versa. (Voir ci-dessous pour obtenir une description mathématique de ces lois.) Parmi les quatre équations, deux d'entre eux, la loi de Gauss et La loi de Gauss pour le magnétisme, décrivent comment les champs émanent de charges. (Pour le champ magnétique il ne ya aucun frais magnétique et les lignes de champs magnétiques donc ni commencer ni finir ne importe où.) Les deux autres équations décrivent comment de l'circuler »les champs autour de leurs sources respectives; le champ magnétique «circule» autour de courants et de temps électriques champ électrique variable dans La loi d'Ampère avec correction de Maxwell, tandis que «circule» du champ électrique autour de temps variant champs magnétiques dans La loi de Faraday.

La loi de Gauss

La loi de Gauss décrit la relation entre un champ électrique et les génératrices de charges électriques : Les points de champ électrique loin de charges positives et vers charges négatives. Dans la description des lignes de champ, les lignes de champ électrique commencent seulement à des charges électriques positives et ne se terminent à des charges électriques négatives. «Comptage» le nombre de lignes de champ dans un surface fermée, donc, donne la charge totale délimitée par cette surface. Plus techniquement, il concerne la flux électrique à travers toute hypothétique fermée " Surface de Gauss "à la charge électrique à l'intérieur de la surface.

La loi de Gauss pour le magnétisme: lignes de champ magnétique ne commencent jamais ni fin, mais forment des boucles ou se étendent à l'infini comme montré ici avec le champ magnétique dû à un anneau de courant.

La loi de Gauss à magnétisme

La loi de Gauss pour le magnétisme déclare qu'il n'y a pas "charges magnétiques" (également appelés monopôles magnétiques), analogues aux charges électriques. Au lieu de cela, le champ magnétique dû aux matériaux est généré par une configuration appelée dipôle. Dipôles magnétiques sont mieux représentés que les boucles de courant, mais ressemblent à des «charges magnétiques» positives et négatives, inséparablement liés entre eux, ne ayant pas de «charge magnétique net. En termes de lignes de champ, cette équation indique que les lignes de champ magnétique ne commencent ni fin, mais faire des boucles ou se étendent à l'infini et à l'arrière. En d'autres termes, une ligne de champ magnétique qui pénètre dans un volume donné doit sortir quelque part ce volume. États techniques équivalentes sont que le total flux magnétique à travers ne importe quelle surface gaussienne est égale à zéro, ou que le champ magnétique est un Champ solénoïdal.

La loi de Faraday

Dans un tempête géomagnétique, une augmentation du flux de particules chargées modifie temporairement le champ magnétique de la Terre, ce qui induit des champs électriques dans l'atmosphère de la Terre, causant ainsi poussées dans notre électrique les réseaux électriques.

La loi de Faraday décrit comment une variable dans le temps champ magnétique crée («induit») d'un champ électrique . Cet aspect de induction électromagnétique est le principe de fonctionnement derrière beaucoup générateurs électriques: par exemple une rotation bar aimant crée un champ magnétique changeant, qui à son tour génère un champ électrique dans un fil à proximité. (Note: il ya deux équations étroitement liés qui sont appelés la loi de Faraday La forme utilisée dans les équations de Maxwell est toujours valide, mais plus restrictive que celle formulée à l'origine par. Michael Faraday .)

La loi d'Ampère avec correction de Maxwell

Un de Wang La mémoire de noyau magnétique (1954) est une application de La loi d'Ampère. Chaque magasins base une peu de données.

La loi d'Ampère avec la correction de Maxwell indique que les champs magnétiques peuvent être générés de deux façons: par courant électrique (ce était la «loi de Ampère" original) et en modifiant des champs électriques (ce était "la correction de Maxwell").

La correction de Maxwell à la loi d'Ampère est particulièrement important: Cela signifie qu'un champ magnétique changeant crée un champ électrique et un champ électrique changeant crée un champ magnétique. Par conséquent, ces équations permettent "autonomes ondes électromagnétiques "de voyager à travers l'espace vide (voir Rayonnement électromagnétique).

La vitesse calculée pour les ondes électromagnétiques, ce qui pourrait être prédite à partir des expériences sur des charges et des courants, correspond exactement à la vitesse de la lumière ; En effet, la lumière est une forme de rayonnement électromagnétique (comme le sont rayons X, les ondes radio, et autres). Maxwell compris la connexion entre les ondes électromagnétiques et la lumière en 1861, unifiant ainsi les domaines précédemment séparés de l'électromagnétisme et l'optique .

Unités et résumé des équations

Les équations de Maxwell varient avec le système d'unités utilisé. Bien que la forme générale reste la même, diverses définitions se changer et des constantes apparaissent à différents endroits. Les équations de cette section sont donnés dans Unités SI. D'autres unités sont couramment utilisés Unités de Gauss (basés sur le système de CGS), Unités de Lorentz-Heaviside (utilisés principalement dans la physique des particules) et Unités de Planck (utilisés en physique théorique). Voir ci-dessous Unités CGS de Gauss.

Pour une description de la différence entre les variantes microscopiques et macroscopiques des équations de Maxwell voir les sections pertinentes ci-dessous.

Dans les équations ci-dessous, les symboles en gras représentent vecteur quantités, et les symboles en italique représentent quantités scalaires. Les définitions des termes utilisés dans les deux tableaux d'équations sont donnés dans une autre table, immédiatement après.

Table des équations microscopiques ''

Formulation en termes de charge et de courant *total*
Nom	Forme différentielle	Forme intégrale
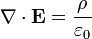La loi de Gauss	$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$	$\ Int \ \ \ \ \ \ \ \ \;!!!!!!!! \ \;! \ \ Subset \; \ \;! \ \ \;! \ \ \ \ \!!!!! \ \ \ int _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \; \; \ ! \ \ supset \ mathbf E \; \ cdot \ mathrm {d} \ mathbf A = \ frac {Q (V)} {\ varepsilon_0}$
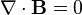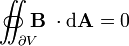La loi de Gauss à magnétisme	$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Int \ \ \ \ \ \ \ \ \;!!!!!!!! \ \;! \ \ Subset \; \ \;! \ \ \;! \ \ \ \ \!!!!! \ \ \ int _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \; \; \ ! \ \ supset \ mathbf B \; \ cdot \ mathrm {d} \ mathbf A = 0$
Équation de Maxwell-Faraday (Loi de Faraday de l'induction)	$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$	$\ Oint _ {\ S partielle} \ de mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ partial t}$
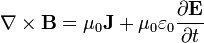Théorème d'Ampère (Avec correction de Maxwell)	$\ Nabla \ times \ mathbf {B} = \ mu_0 \ mathbf {J} + \ mu_0 \ varepsilon_0 \ frac {\ partial \ mathbf {E}} {\ partial t} \$	$\ Oint _ {\ S partielle} \ de mathbf {B} \ cdot \ mathrm {d} \ mathbf {l} = \ mu_0 I_S + \ mu_0 \ varepsilon_0 \ frac {\ partial \ Phi_ {E, S}} {\ partial t }$

Table des équations macroscopiques ''

Formulation en termes de charge et de courant *libre*
Nom	Forme différentielle	Forme intégrale
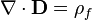La loi de Gauss	$\ Nabla \ cdot \ mathbf {D} = \ rho_f$	$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf D \;! \ cdot \ mathrm {d} \ mathbf A = Q_ {f} (V)$
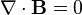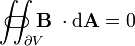La loi de Gauss à magnétisme	$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A = 0$
Équation de Maxwell-Faraday ( La loi d'induction de Faraday)	$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$	$\ Oint _ {\ S partielle} \ de mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ partial t}$
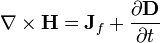Théorème d'Ampère (Avec correction de Maxwell)	$\ Nabla \ times \ mathbf {H} = \ mathbf {J} _f + \ frac {\ partial \ mathbf {D}} {\ partial t}$	$\ Oint _ {\ S partielle} \ mathbf {H} \ cdot \ mathrm {d} \ mathbf {l} = I_ {f, S} + \ frac {\ partial \ Phi_ {D, S}} {\ partial t}$

Table des termes utilisés dans les équations de Maxwell

Le tableau suivant donne la signification de chaque symbole et le Unité de mesure SI:

Définitions et unités
Symbole	Signification (premier terme est le plus commun)	SI Unité de mesure
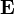$\ Mathbf {E} \$	champ électrique appelé également l'intensité du champ électrique	volt par mètres ou, de façon équivalente, par Newton Coulomb
$\ Mathbf {B} \$	champ magnétique également appelé l'induction magnétique également appelé la densité de champ magnétique également appelé la densité de flux magnétique	tesla, ou de manière équivalente, weber par mètre carré, volts - seconde par mètre carré
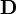$\ Mathbf {D} \$	Induction électrique également appelé l'induction électrique également appelé la densité de flux électrique	coulombs par mètre carré ou de manière équivalente, newton par volts - mètre
$\ Mathbf {H} \$	champ magnétisant aussi appelé champ magnétique auxiliaire également appelé intensité du champ magnétique aussi appelé champ magnétique	ampère par mètre
$\ Mathbf {\ nabla \ cdot}$	la divergence opérateur	par mètre (facteur a contribué en appliquant soit l'opérateur)
$\ Mathbf {\ nabla \ times}$	la boucle opérateur
$\ Frac {\ partial} {\ partial t}$	dérivée partielle par rapport au temps	par seconde (facteur a contribué en appliquant l'opérateur)
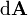$\ Mathrm {d} \ mathbf {A}$	élément de vecteur différentiel de la zone surface A, avec infiniment petit ampleur et la direction perpendiculaire à la surface S	mètres carrés
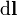$\ Mathrm {d} \ mathbf {l}$	élément de vecteur différentiel de longueur du chemin tangentielle au chemin / courbe	mètres
$\ Varepsilon_0 \$	permittivité de l'espace libre, appelé aussi constante électrique, une constante universelle	farads par mètre
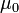$\ Mu_0 \$	perméabilité de l'espace libre, appelé aussi magnétique constant, une constante universelle	henrys par mètre, ou newtons par ampère carré
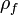$\ \ Rho_f \$	gratuit densité de charge (non compris charges liées)	coulombs par mètre cube
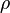$\ \ Rho \$	total densité de charge (y compris à la fois libre et charges liées)	coulombs par mètre cube
$\ Mathbf {J} _f$	gratuit densité de courant (non compris courant lié)	ampères par mètre carré
$\ Mathbf {J}$	total densité de courant (y compris à la fois libre et courant lié)	ampères par mètre carré
$\, Q_f (V)$	net sans charge électrique dans le volume V en trois dimensions (non compris charges liées)	Coulombs
$\, Q (V)$	net charge électrique dans le volume V en trois dimensions (y compris à la fois libre et charges liées)	Coulombs
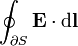$\ Oint _ {\ S partielle} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l}$	intégrale curviligne du champ électrique le long de la ∂S limites d'une surface S (∂S est toujours une courbe fermée ).	joules par coulomb
$\ Oint _ {\ S partielle} \ de mathbf {B} \ cdot \ mathrm {d} \ mathbf {l}$	ligne intégrante du champ magnétique sur les ∂S frontière fermée de la surface S	Tesla mètres
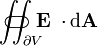$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf E \;! \ cdot \ mathrm {d} \ mathbf A$	la flux électrique ( intégrale de surface du champ électrique) à travers la ( surface fermée) $\ Partial V$ (La limite du volume V)	joule-coulomb mètre par
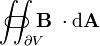$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A$	la flux magnétique ( intégrante de la surface du champ magnétique B) à travers la ( surface fermée) $\ Partial V$ (La limite du volume V)	tesla mètres-carré ou webers
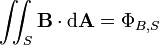$\ Iint_S \ mathbf {B} \ cdot \ mathrm {d} \ mathbf {A} = \ Phi_ {B, S}$	flux magnétique à travers ne importe quelle surface S, pas nécessairement fermé	webers ou équivalente, volts-seconde
$\ Iint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ {Phi_ E, S}$	flux électrique à travers ne importe quelle surface S, pas nécessairement fermé	Joule-mètres par coulomb
$\ Iint_S \ mathbf {D} \ cdot \ mathrm {d} \ mathbf {A} = \ Phi_ {D, S}$	flux de champ de déplacement électrique à travers ne importe quelle surface S, pas nécessairement fermé	Coulombs
$\ Iint_S \ mathbf {J} _f \ cdot \ mathrm {d} \ mathbf {A} = I_ {f, s}$	net gratuit un courant électrique passant à travers la surface S (à l'exclusion courant lié)	Ampère
$\ Iint_S \ mathbf {J} \ cdot \ mathrm {d} \ mathbf {A} = I_ {S}$	net passage de courant électrique à travers la surface S (incluant à la fois libre et courant lié)	Ampère

Preuve que les deux formulations générales sont équivalentes

Les deux formulations générales suppléants des équations de Maxwell données ci-dessus sont mathématiquement équivalentes et liés par les relations suivantes:

$\ Rho_b = - \ nabla \ cdot \ mathbf {P},$

$\ Mathbf {J} _b = \ nabla \ times \ mathbf {M} + \ frac {\ partial \ mathbf {P}} {\ t partielle},$

$\ Mathbf {D} = \ epsilon_0 \ mathbf {E} + \ mathbf {P},$

$\ Mathbf {B} = \ mu_0 (\ mathbf {H} + \ mathbf {M}),$

$\ Rho = \ rho_b + \ rho_f, \$

$\ Mathbf {J} = \ mathbf {J} _b + \ mathbf {J} _f,$

où P et M sont polarisation et aimantation, et ρ _b et _b J sont liés courant de charge et, respectivement. En substituant ces équations dans les équations »macroscopiques» de Maxwell donne identique les équations microscopiques.

Équations «microscopiques» de Maxwell

La variante microscopique de l'équation de Maxwell exprime le champ électrique E et le champ magnétique B en fonction de la charge totale et présente courant total, y compris les charges et des courants au niveau atomique. Elle est parfois appelée la forme générale des équations de Maxwell ou «équations de Maxwell dans le vide". Les deux variantes des équations de Maxwell sont tout aussi général, cependant, car ils sont mathématiquement équivalentes. Les équations microscopiques sont les plus utiles dans des guides d'ondes, par exemple, en l'absence de matériaux diélectriques ou magnétiques à proximité.

Formulation en termes de charge et de courant *total*
Nom	Forme différentielle	Forme intégrale
La loi de Gauss	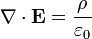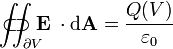$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$	$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf E \;! \ cdot \ mathrm {d} \ mathbf A = \ frac {Q (V)} {\ varepsilon_0}$
La loi de Gauss à magnétisme	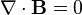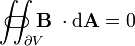$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A = 0$
Équation de Maxwell-Faraday (Loi de Faraday de l'induction)	$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$	$\ Oint _ {\ S partielle} \ de mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ partial t}$
Théorème d'Ampère (Avec correction de Maxwell)	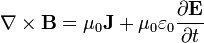$\ Nabla \ times \ mathbf {B} = \ mu_0 \ mathbf {J} + \ mu_0 \ varepsilon_0 \ frac {\ partial \ mathbf {E}} {\ partial t} \$	$\ Oint _ {\ S partielle} \ de mathbf {B} \ cdot \ mathrm {d} \ mathbf {l} = \ mu_0 I_S + \ mu_0 \ varepsilon_0 \ frac {\ partial \ Phi_ {E, S}} {\ partial t }$

Avec ni charges ni courants

Dans une région sans frais (ρ = 0) et aucun courant (J = 0), comme dans un vide, les équations de Maxwell réduisent à:

$\ Nabla \ cdot \ mathbf {} E = 0$

$\ Nabla \ cdot \ mathbf {B} = 0$

$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$

$\ Nabla \ times \ mathbf {B} = \ \ \ mu_0 \ varepsilon_0 \ frac {\ partial \ mathbf {E}} {\ t partielle}.$

Ces équations conduisent directement à E et B satisfaisant la équation d'onde pour laquelle les solutions sont des combinaisons linéaires de ondes planes voyageant à la vitesse de la lumière ,

$c = \ frac {1} {\ sqrt {\ mu_0 \ varepsilon_0}}. \$

En outre, E et B sont mutuellement perpendiculaires entre eux et la direction de déplacement et sont en phase les uns avec les autres. Un sinusoïdale onde plane est une solution spéciale de ces équations.

En fait, les équations de Maxwell expliquent comment ces ondes peuvent physiquement se propager à travers l'espace. Le champ magnétique changeant crée un champ électrique à travers l'évolution La loi de Faraday. À son tour, ce champ électrique crée un champ magnétique changeant travers La correction de Maxwell à la loi d'Ampère. Ce cycle perpétuel permet à ces vagues, maintenant connu sous le rayonnement électromagnétique , de se déplacer dans l'espace à la vitesse c.

'' Équations macroscopiques de Maxwell

Contrairement aux équations «microscopiques», «équations macroscopiques de Maxwell", aussi connu comme les équations de Maxwell dans la matière, le facteur sur la charge liée et actuelle pour obtenir des équations qui ne dépendent que des charges et des courants gratuits. Ces équations sont plus semblables à ceux que Maxwell se est présenté. Le coût de cette factorisation est que les champs supplémentaires doivent être définis: le champ de déplacement D qui est définie en termes de champ électrique E et le polarisation P du matériau, et le champ Magnétiques- de H, qui est définie en termes de champ et le B Magnétiques- aimantation M du matériau.

Courant de charge et Bound

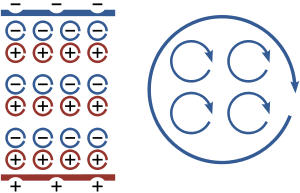
Gauche: Une vue schématique de la façon dont un ensemble de dipôles microscopiques produit des charges de surface opposées comme indiqué en haut et en bas à droite:. Comment un assemblage de boucles de courant microscopiques ajouter ensemble pour produire une boucle de courant circulant macroscopiquement. A l'intérieur des frontières, les contributions individuelles tendent à se annuler, mais aux limites aucune annulation survient.

Lorsqu'un champ électrique est appliqué à un matériau diélectrique ses molécules réagissent en formant microscopique leurs dipôles-électriques noyaux atomiques se déplacent d'une courte distance dans la direction du champ, tandis que les électrons se déplacent d'une courte distance dans la direction opposée. Cela produit une charge liée macroscopique dans le matériau même si tous les faits reprochés sont liés à des molécules individuelles. Par exemple, si chaque molécule répond identique, analogue à celui représenté sur la figure, ces petits mouvements de la charge se combinent pour produire une couche de positif lié charge sur un côté de la matière et une couche de charge négative de l'autre côté. La charge liée est plus commodément décrite en termes d'un polarisation, P, dans le matériau. Si P est uniforme, une séparation macroscopique de charge est produite uniquement sur les surfaces où P entrer et sortir de la matière. Pour P non uniforme, une charge est également produit dans la masse.

Un peu similaire, dans tous les matériaux constitutifs de la atomes exposition moments magnétiques qui sont intrinsèquement liés à la moment angulaire des composants des atomes, notamment leurs électrons. Le connexion au moment angulaire suggère l'image d'un ensemble de boucles de courant microscopiques. En dehors de la matière, un ensemble de ces boucles de courant microscopiques ne est pas différent d'un courant macroscopique de circulation autour de la surface de la matière, malgré le fait qu'aucun moment magnétique individuel se déplace d'une distance importante. Ces courants liés peuvent être décrites en utilisant la aimantation M.

Le très compliqué et granulaires lié charges et des courants consolidés, donc peuvent être représentés à l'échelle macroscopique en termes de P et M dont la moyenne de ces charges et de courants sur une échelle suffisamment grande pour ne pas voir la granularité des atomes individuels, mais aussi suffisamment petites qu'elles varient en fonction de l'emplacement dans le matériau. En tant que tel, les équations de Maxwell macroscopiques ignore beaucoup de détails sur une échelle fine qui peut être sans importance pour comprendre les questions sur une échelle de grosser en calculant les champs qui sont moyennées sur un peu de volume de taille appropriée.

Équations

Formulation en termes de charge et de courant *libre*
Nom	Forme différentielle	Forme intégrale
La loi de Gauss	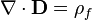$\ Nabla \ cdot \ mathbf {D} = \ rho_f$	$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf D \;! \ cdot \ mathrm {d} \ mathbf A = Q_ {f} (V)$
La loi de Gauss à magnétisme	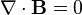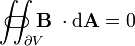$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Iint _ {\ V partielle} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A = 0$
Équation de Maxwell-Faraday ( La loi d'induction de Faraday)	$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$	$\ Oint _ {\ S partielle} \ de mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ partial t}$
Théorème d'Ampère (Avec correction de Maxwell)	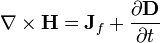$\ Nabla \ times \ mathbf {H} = \ mathbf {J} _f + \ frac {\ partial \ mathbf {D}} {\ partial t}$	$\ Oint _ {\ S partielle} \ mathbf {H} \ cdot \ mathrm {d} \ mathbf {l} = I_ {f, S} + \ frac {\ partial \ Phi_ {D, S}} {\ partial t}$

Relations constitutives

Afin d'appliquer 'équations macroscopiques de Maxwell », il est nécessaire de préciser les relations entre champ de déplacement D et E, et le H-champ magnétique H et B. Ces équations indiquent la réponse de charge et de courant liée aux domaines appliqués et sont appelés relations constitutives.

Détermination de la relation entre les champs de comportement auxiliaires D et H et les champs E et B commence par la définition des champs auxiliaires eux-mêmes:

$\ Mathbf {D} (\ mathbf {r}, t) = \ epsilon_0 \ mathbf {E} (\ mathbf {r}, t) + \ mathbf {P} (\ mathbf {r}, t)$

$\ Mathbf {H} (\ mathbf {r}, t) = \ frac {1} {\ mu_0} \ mathbf {B} (\ mathbf {r}, t) - \ mathbf {M} (\ mathbf {r} , t),$

où P est la champ de polarisation et M est la champ d'aimantation qui sont définis en termes de frais de microscopiques lié et le courant lié respectivement. Avant d'arriver à la façon de calculer M et P, il est utile d'examiner certains cas particuliers, cependant.

Sans matériaux magnétiques ou diélectriques

En l'absence de matériaux magnétiques ou diélectriques, les relations constitutives sont simples:

$\ Mathbf {D} = \ epsilon_0 \ mathbf {e}, \; \; \; \ Mathbf {H} = \ mathbf {B} / \ mu_0$

où ε ₀ et μ ₀ sont deux constantes universelles, appelé permittivité espace libre et perméabilité de l'espace libre, respectivement. En substituant ces dos en équations macroscopiques de Maxwell mènent directement à des équations de Maxwell microscopiques, sauf que les courants et les charges sont remplacés par des courants libres et charges libres. Ce est prévu car il n'y a aucun frais reliés ni courants.

Matériaux isotrope linéaire

Dans un ( isotrope) de matériau linéaire, où P est proportionnelle à E et M est proportionnel à B les relations constitutives sont également simple. En termes de polarizaton P et l'aimantation M ils sont:

$\ Mathbf {P} = \ epsilon_0 \ chi_e \ mathbf {e}, \; \; \; \ Mathbf {M} = \ chi_m \ mathbf {} H,$

où χ χ _e et _m sont électrique et susceptibilités magnétiques d'un matériau donné, respectivement. En termes de D et H les relations constitutives sont:

$\ Mathbf {D} = \ epsilon \ mathbf {e}, \; \; \; \ Mathbf {H} = \ mathbf {B} / \ mu,$

où ε et μ sont des constantes (qui dépendent de la matière), appelé le permittivité et perméabilité, respectivement, du matériau. Ceux-ci sont liés aux susceptibilités par:

$\ Epsilon = \ epsilon_0 (1+ \ chi_e) \; \; \; \ Mu = \ mu_0 (1+ \ chi_m)$

En substituant dans les relations constitutives ci-dessus dans les équations de Maxwell en linéaires, dispersionless, matériaux invariants dans le temps (forme différentielle seulement) sont:

$\ Nabla \ cdot (\ epsilon \ mathbf {E}) = \ rho_f$

$\ Nabla \ cdot \ mathbf {B} = 0$

$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$

$\ nabla \ times (\ mathbf {B} / \ mu) = \ mathbf {J} _f + \ epsilon \ frac {\ partial \ mathbf {E}} {\ t partielle}.$

Ce sont formellement identique à la formulation générale en termes de E et B (ci-dessus), sauf que le permittivité espace libre a été remplacé par le permittivité du matériau, la perméabilité de l'espace libre a été remplacé par le charges et des courants libres de perméabilité de la matière, et seuls sont inclus (au lieu de tous les frais et les courants). Sauf que le matériau est homogène dans l'espace, ε et μ ne peuvent pas être les exclure de l'expressions dérivés sur les côtés gauche.

Cas général

Pour les matériaux du monde réel, les relations constitutives ne sont pas linéaires, sauf environ. Calcul des relations constitutives de premiers principes consiste à déterminer la façon dont P et M sont créés à partir d'un E et B donné. Ces relations peuvent être empirique (fondée directement sur mesures), ou théorique (basé sur la mécanique statistique , la théorie du transport ou d'autres outils de la physique de la matière condensée ). Le détail peut être employé macroscopique ou microscopique, selon le niveau nécessaire pour le problème sous examen.

En général, si les relations constitutives peuvent généralement encore être écrits:

$\ Mathbf {D} = \ epsilon \ mathbf {e}, \; \; \; \ Mathbf {H} = \ mathbf {B} / \ mu$

mais ε et μ ne sont pas, en général, constantes simples, mais plutôt fonctions. Des exemples sont les suivants:

Dispersion et absorption où ε et μ sont des fonctions de la fréquence. (Causalité ne permet pas de matériaux pour être non dispersif; voir, par exemple, Kramers-Kronig relations). Ni le font les champs doivent être en phase qui conduit à ε et μ étant complexe . Cela conduit également à l'absorption.
Bi (e) isotropie où H et D dépendent à la fois B et E:

$D = \ epsilon E + \ xi H \; \; \; B = \ mu H + \ zeta E.$

Non-linéarité où ε et μ sont des fonctions de E et B.
Anisotropie (tels que biréfringence ou dichroïsme) qui se produit lorsque ε et μ sont de second rang tenseurs,

$D_j = \ epsilon_ {} ij E_i \; \; \; B_j = \ mu_ {} ij h_i.$

Dépendance de P et M sur E et B à d'autres endroits et les heures. Cela pourrait être dû au manque d'homogénéité spatiale; par exemple dans un la structure domained, hétérostructure ou un cristal liquide , ou le plus souvent dans la situation où il n'y a simplement plusieurs matériaux occupant différentes régions de l'espace). Ou cela peut être dû à un milieu variant de temps ou du fait de hystérésis. Dans un tel cas, P et M peut être calculée comme suit:

$\ Mathbf {P} (\ mathbf {r}, t) = \ epsilon_0 \ int {\ rm d} ^ 3 \ mathbf {r} '{\ rm d} t \'; \ Hat {\ chi} _ {\ mathrm {}} elec (\ mathbf {r}, \ mathbf {r} ', t, t'; \ mathbf {E}) \, \ mathbf {E} (\ mathbf { r} ', t')$

$\ Mathbf {M} (\ mathbf {r}, t) = \ frac {1} {\ mu_0} \ int {\ rm d} ^ 3 \ mathbf {r} '{\ rm d} t \'; \ Hat {\ chi} _ {\ mathrm {}} magn (\ mathbf {r}, \ mathbf {r} ', t, t'; mathbf \ {B}) \, \ mathbf {B} (\ mathbf { r} ', t'),$

dans lequel les fonctions de la permittivité et la perméabilité sont remplacés par des intégrales sur la plus générale électrique et susceptibilités magnétiques.

Dans la pratique, certaines propriétés des matériaux ont un impact négligeable dans des circonstances particulières, permettant la négligence de petits effets. Par exemple: non-linéarités optiques peuvent être négligés pour les faibles intensités de champ; dispersion par la matière est sans importance lorsque la fréquence est limitée à un étroit la bande passante; absorption de la matière peut être négligé pour des longueurs d'onde pour lesquelles un matériau est transparent; et métaux avec conductivité finie sont souvent estimés à micro-ondes ou des longueurs d'onde plus longues que métaux parfaits avec une conductivité infinie (formant barrières dures avec zéro la profondeur de la peau de la pénétration sur le terrain).

On peut noter que les matières synthétiques peuvent être conçus pour avoir une permittivité et une perméabilité sur mesure, tel que métamatériaux et des cristaux photoniques.

Calcul des relations constitutives

En général, les équations constitutives sont théoriquement déterminées par le calcul de la façon dont une molécule répond aux champs locaux par l'intermédiaire du Force de Lorentz. Peuvent avoir besoin d'être modélisés aussi bien comme vibrations réseaux dans les cristaux ou des forces d'obligations d'autres forces. Y compris toutes les forces conduit à des changements dans la molécule qui sont utilisées pour calculer P et M en fonction des champs locaux.

Les champs locaux diffèrent des champs appliqués en raison des champs produits par la polarisation et l'aimantation du matériau à proximité; un effet qui doit également être modélisé. En outre, des matériaux réels ne sont pas milieux continus; les champs locaux de matériaux réels varient énormément à l'échelle atomique. Les champs doivent être mesurées sur un volume approprié pour former une approximation de continuum.

Ces approximations du continuum nécessitent souvent un certain type de mécanique quantique analyse tels que la théorie quantique des champs appliquée à la physique de la matière condensée . Voir, par exemple, théorie de la fonctionnelle de la densité, Relations-Kubo vert et La fonction de Green. Diverses équations de transport approximatives ont évolué, par exemple, la Équation de Boltzmann ou de la Équation de Fokker-Planck ou Équations de Navier-Stokes. Certains exemples de ces équations sont appliquées sont magnétohydrodynamique, la dynamique des fluides, électrohydrodynamique, la supraconductivité , modélisation du plasma. Un ensemble de l'appareil physique pour traiter ces questions se est développée. Une autre série de méthodes d'homogénéisation (évolution d'une tradition dans les matériaux tels que le traitement des conglomérats et stratifiés) sont basés sur le rapprochement d'un matériau inhomogène par un homogène milieu effectif (valable pour excitations avec longueurs d'onde beaucoup plus grande que l'échelle de l'hétérogénéité).

La modélisation théorique des propriétés continuum-approximation de nombreux matériaux réels comptent souvent sur la mesure ainsi, par exemple, les mesures d'ellipsométrie.

Histoire

Relation entre l'électricité, le magnétisme et la vitesse de la lumière

La relation entre l'électricité, le magnétisme et la vitesse de la lumière peut être résumée par l'équation moderne:

$c = \ frac {1} {\ sqrt {\ mu_0 \ varepsilon_0}} \.$

Le côté gauche est la vitesse de la lumière, et de la droite est une grandeur liée à des équations régissant l'électricité et le magnétisme. Bien que la droite a des unités de vitesse, il peut être déduit à partir des mesures de forces électriques et magnétiques, qui impliquent aucun vitesses physiques. Par conséquent, l'établissement de cette relation fourni des preuves convaincantes que la lumière est un phénomène électromagnétique.

La découverte de cette relation a commencé en 1855, lorsque Wilhelm Eduard Weber et Rudolf Kohlrausch déterminé qu'il y avait une quantité liée à l'électricité et le magnétisme, "le rapport de l'unité électromagnétique de charge absolu à l'unité électrostatique de charge absolu" (en langage moderne, la valeur 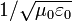$1 / \ sqrt {\ mu_0 varepsilon_0 \}$ ), Et déterminé qu'il devrait avoir des unités de vitesse. Ils ont ensuite mesuré ce rapport par une expérience qui a impliqué une charge et de décharge Bouteille de Leyde et de mesure de la force magnétique du courant de décharge, et a trouvé une valeur 3,107 × 10 ⁸ m / s, remarquablement proches de la vitesse de la lumière, qui a récemment été évalués à 3,14 × 10 ⁸ m / s par Hippolyte Fizeau en 1848 et à 2,98 × 10 ⁸ m / s par Léon Foucault en 1850. Cependant, Weber et Kohlrausch n'a pas fait la connexion à la vitesse de la lumière. Vers la fin de 1861 tout en travaillant sur la partie III de son document Sur les lignes de la force physique, Maxwell a voyagé de l'Ecosse à Londres et leva les yeux Weber et les résultats de Kohlrausch. Il les transforme en un format qui est compatible avec ses propres écrits, et, ce faisant, il établit la connexion à la vitesse de la lumière et a conclu que la lumière est une forme de rayonnement électromagnétique.

Les équations de Maxwell Le terme

Les quatre équations de Maxwell modernes peuvent être trouvés individuellement tout au long de son article 1861, dérivée théoriquement en utilisant un modèle de vortex moléculaire de Michael Faraday de l '«lignes de force» et en collaboration avec le résultat expérimental de Weber et Kohlrausch. Mais ce ne est qu'en 1884 que Oliver Heaviside, en même temps que des travaux similaires par Willard Gibbs et Heinrich Hertz, regroupé les quatre ensemble dans un ensemble distinct. Ce groupe de quatre équations était connue diversement comme les équations Hertz-Heaviside et les équations de Maxwell-Hertz, et sont parfois encore connu que les équations de Maxwell-Heaviside.

La contribution de Maxwell à la science dans la production de ces équations réside dans la correction qu'il a faite à Théorème d'Ampère dans son document de 1861 Sur les lignes de la force physique. Il a ajouté que mandat actuel déplacement à Théorème d'Ampère et cela lui a permis de tirer le Rayonnement électromagnétique dans son article ultérieur 1865 Une théorie dynamique du champ électromagnétique et de démontrer le fait que la lumière est une onde électromagnétique . Ce fait a été confirmé plus tard puis expérimentalement par Heinrich Hertz en 1887. Le physicien Richard Feynman a prédit que, "La guerre civile américaine sera pâle dans l'insignifiance provinciale par rapport à cet événement scientifique important de la même décennie."

. Le concept de champs a été introduit par, entre autres, Faraday Albert Einstein a écrit:

La formulation précise des lois l'espace-temps était l'œuvre de Maxwell. Imaginez ses sentiments lorsque les équations différentielles qu'il avait formulées lui prouvèrent que les champs électromagnétiques répartis sous la forme d'ondes polarisées, et à la vitesse de la lumière! Pour quelques hommes dans le monde a été une telle expérience daigné ... il a fallu des décennies pour certains physiciens saisir la pleine signification de la découverte de Maxwell, si audacieux était le saut que son génie forcé sur les conceptions de ses collaborateurs
- (Science, 24 mai 1940)

Heaviside a travaillé pour éliminer les potentiels ( potentiel électrique et potentiel magnétique) que Maxwell avait utilisé les concepts centraux dans ses équations; cet effort a été quelque peu controversé, mais il a été entendu par 1884 que les potentiels doivent se propagent à la vitesse de la lumière comme les champs, à la différence du concept de l'action instantanée-à-la-loin, comme à l'époque de la conception potentiel gravitationnel. Analyse moderne, par exemple, des antennes radio, fait pleinement usage de vecteurs et scalaires les potentiels de Maxwell pour séparer les variables, une technique couramment utilisée dans la formulation des solutions d'équations différentielles. Cependant les potentiels peuvent être introduits par manipulation algébrique des quatre équations fondamentales.

Sur les lignes de la force physique

Les quatre équations de Maxwell jours modernes sont apparus tout au long de 1861 papier de Maxwell sur les lignes de la force physique:

L'équation (56) en 1861 papier de Maxwell est ∇ ⋅ B = 0.
L'équation (112) est Théorème d'Ampère avec le courant de déplacement de Maxwell ajouté. Ce est l'addition de courant de déplacement qui est l'aspect le plus important du travail de Maxwell en électromagnétisme , car il lui a permis de tirer plus tard, le Rayonnement électromagnétique dans son article 1865 Une théorie dynamique du champ électromagnétique, et donc montrent que la lumière est une onde électromagnétique. Il est donc cet aspect de l'œuvre de Maxwell qui donne les équations leur pleine signification. (Fait intéressant, Kirchhoff dérivé du les équations de télégraphistes en 1857 sans utiliser courant de déplacement. Mais il ne utiliser l'équation de Poisson et l'équation de continuité qui sont les ingrédients mathématiques de la courant de déplacement. Néanmoins, Kirchhoff croyait ses équations pour être applicable seulement à l'intérieur d'un fil électrique et donc il ne est pas crédité d'avoir découvert que la lumière est une onde électromagnétique).
L'équation (115) est la loi de Gauss .
L'équation (54) est une équation qui Oliver Heaviside dénommée «la loi de Faraday. Cette équation répond pour le moment aspect de l'induction électromagnétique variable, mais pas pour l'aspect dynamiquement induite, alors que la loi de Faraday flux d'origine adresse à ces deux aspects. Maxwell traite de l'aspect dynamiquement dépendante de l'induction électromagnétique, v × B , à l'équation (77). L'équation (77), qui est le même que l'équation (D) dans les huit équations de Maxwell initiales énumérées ci-dessous, correspond à toutes fins utiles à la modernité loi de force de jour F = q ( E + v × B ) qui se trouve à côté des équations de Maxwell et porte le nom force de Lorentz, même si Maxwell dérivé quand Lorentz était encore un jeune garçon.

La différence entre leBet lesHvecteurs peut être retracée à 1855 papier de Maxwell intituléSur les lignes de Faraday de la Forcequi a été lu à la Cambridge Philosophical Society. Le document présenté un modèle simplifié des travaux de Faraday, et comment les deux phénomènes étaient liés.Il a réduit l'ensemble des connaissances actuelles dans un ensemble lié deéquations différentielles.

Figure du modèle de vortex moléculaire de Maxwell. Pour un champ magnétique uniforme, les lignes de champ pointent vers l'extérieur à partir de l'écran d'affichage, comme on peut l'observer à partir des points noirs dans le milieu des hexagones. Le vortex de chaque molécule hexagonale tourne dans le sens antihoraire. Les petits cercles verts sont tournant à droite particules en sandwich entre les tourbillons moléculaires.

Il est ensuite précisé dans son concept d'une mer de tourbillons moléculaires qui apparaît dans son papier 1861 Sur les lignes de la force physique. Dans ce contexte, H représenté tourbillon pur (spin), tandis que B était un tourbillon pondérée qui a été pondéré pour la densité de la mer de vortex. Maxwell considéré perméabilité magnétique μ comme une mesure de la densité de la mer à tourbillon. Ainsi la relation,

Courant d'induction magnétiqueprovoque une densité de courant magnétique
$\mathbf{B} = \mu \mathbf{H}$
était essentiellement une analogie de rotation à la relation courant électrique linéaire,
Courant électrique à convection
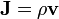
$\mathbf{J} = \rho \mathbf{v}$

où ρ est la densité de charge électrique. B a été vu comme une sorte de courant magnétique de tourbillons alignés dans leurs plans axiaux, avec H étant la vitesse circonférentielle des tourbillons. Avec μ représentant la densité de vortex, il en résulte que le produit de μ avec tourbillon H conduit à la champ magnétique désigné par B .

L'équation courant électrique peut être considéré comme un courant de convection de charge électrique qui implique un mouvement linéaire. Par analogie, l'équation magnétique est un courant inductif impliquant de spin. Il n'y a pas de mouvement linéaire dans le courant inducteur le long de la direction de la chambre vecteur. Le courant inductif magnétique représente lignes de force. En particulier, il représente les lignes de force de la loi carrée inverse.

L'extension des considérations ci-dessus confirme que là où B est à H , et où J est de ρ , alors il découle nécessairement de la loi de Gauss et de l'équation de la continuité de la charge que E est de D . c.-à- B parallèles avec E , tandis que H parallèles avec D .

Une théorie dynamique du champ électromagnétique

En 1864 Maxwell publié Une théorie dynamique du champ électromagnétique dans lequel il a montré que la lumière était un phénomène électromagnétique. Confusion sur la durée "les équations de Maxwell" est exacerbée car il est aussi parfois utilisé pour un ensemble de huit équations qui sont apparus dans la partie III de 1864 papier de Maxwell Une théorie dynamique du champ électromagnétique, intitulé "Les équations générales du champ électromagnétique,« un confusion aggravée par la rédaction de six de ces huit équations que trois équations séparées (une pour chacun des axes cartésiens), résultant en vingt et vingt équations inconnues. (Comme indiqué ci-dessus, cette terminologie est pas commun: références modernes à l'expression "les équations de Maxwell» font référence à des retraitements Heaviside.)

Les huit équations de Maxwell originaux peuvent être écrites en notation moderne vecteur comme suit:

(A) La loi des courants totaux

$\mathbf{J}_{tot} = \mathbf{J} + \frac{\partial\mathbf{D}}{\partial t}$

(B) L'équation de la force magnétique

$\mu \mathbf{H} = \nabla \times \mathbf{A}$

Circuital loi (C) Ampère

$\nabla \times \mathbf{H} = \mathbf{J}_\mathrm{tot}$

Force (D) Electromotive créé par convection, induction, et par l'électricité statique. (Ceci est en effet la force de Lorentz)

$\mathbf{E} = \mu \mathbf{v} \times \mathbf{H} - \frac{\partial\mathbf{A}}{\partial t}-\nabla \phi$

(E) L'équation d'élasticité électrique

$\mathbf{E} = \frac{1}{\epsilon} \mathbf{D}$

La loi de (F) Ohm

$\mathbf{E} = \frac{1}{\sigma} \mathbf{J}$

La loi de (G) Gauss

$\nabla \cdot \mathbf{D} = \rho$

(H) L'équation de continuité

$\nabla \cdot \mathbf{J} = -\frac{\partial\rho}{\partial t}$

$\nabla \cdot \mathbf{J}_\mathrm{tot} = 0$

Notation: Hest lechamp magnétisant, qui Maxwell a appelé l'intensité magnétique.; J est le densité de courant (avecJ _totétant le courant total, y compris en cours de déplacement).; Dest lechamp de déplacement (appelé ledéplacement électriquede Maxwell).; ρest ladensité de charge gratuite (appeléequantité d'électricité gratuitepar Maxwell).; Aest lepotentiel magnétique (appeléeimpulsion angulairepar Maxwell).; Eest appelée laforce électromotricepar Maxwell. Le terme force électromotrice est aujourd'hui utilisé pour la tension, mais il est clair à partir du contexte que le sens de Maxwell correspondait plus à l'expression modernechamp électrique.; φest lepotentiel électrique (qui Maxwell a également appelépotentiel électrique).; σest laconductivité électrique (Maxwell a appelé l'inverse de la conductivité de larésistance spécifique, ce qui est maintenant appelé larésistivité).

Il est intéressant de noter leμ v×Hterme qui apparaît dans l'équation équation D. D est donc effectivement laforce de Lorentz, de façon similaire à l'équation (77) de son document de 1861 (voir ci-dessus).

Lorsque Maxwell tire l' équation d'onde électromagnétique dans son document de 1865, il utilise l'équation D pour répondre à induction électromagnétique plutôt que la loi de Faraday de l'induction qui est utilisé dans les manuels modernes. (La loi de Faraday lui-même ne figure pas parmi ses équations.) Cependant, Maxwell laisse tomber le μ v × H terme de l'équation D quand il est dériver l' équation d'onde électromagnétique, comme il considère que la situation de la trame de repos.

Un Traité sur l'électricité et le magnétisme

En Un Traité sur l'électricité et le magnétisme, un 1873traité surl'électromagnétismeécrit parJames Clerk Maxwell, onze équations générales du champ électromagnétique sont répertoriés et ceux-ci comprennent les huit qui sont énumérés dans le document de 1865.

Les équations de Maxwell et de la relativité

Équations de Maxwell originaux sont basés sur l'idée que la lumière se déplace à travers une mer de tourbillons moléculaires connus comme le « éther luminiferous ', et que la vitesse de la lumière doit être respectif pour le cadre de cet éther de référence. Mesures visant à mesurer la vitesse de la Terre à travers l'éther en conflit, si.

Une approche plus théorique a été suggéré par Hendrik Lorentz avec George FitzGerald et Joseph Larmor. Les deux Larmor (1897) et Lorentz (1899, 1904) proviennent de la transformation de Lorentz (ainsi nommée par Henri Poincaré) que celui sous lequel les équations de Maxwell étaient invariant. Poincaré (1900) a analysé la coordination des horloges en mouvement par l'échange de signaux lumineux. Il a également établi mathématiquement la propriété de groupe de la transformation de Lorentz (Poincaré 1905).

Einstein a rejeté l'éther comme inutile et a conclu que les équations de Maxwell prédisent l'existence d'une vitesse fixe de lumière, indépendante de la vitesse de l'observateur, et comme tel il a utilisé les équations de Maxwell comme le point de départ de sa théorie de la relativité . Ce faisant, il a créé la transformation de Lorentz comme étant valable pour toute la matière et non pas seulement des équations de Maxwell. Les équations de Maxwell joué un rôle clé dans le célèbre article d'Einstein sur la relativité spéciale; par exemple, dans le paragraphe du document d'ouverture, il a motivé sa théorie en notant que la description d'un conducteur se déplaçant par rapport à un aimant doit générer un ensemble cohérent de domaines indépendamment du fait que la force est calculée dans le cadre de l'aimant de repos ou celle du conducteur.

Général la relativité a également eu une relation étroite avec les équations de Maxwell. Par exemple, Theodor Kaluza et Oskar Klein montré dans les années 1920 que les équations de Maxwell peut être obtenu en étendant la relativité générale en cinq dimensions. Cette stratégie d'utilisation des dimensions supérieures à unifier les différentes forces reste un domaine de recherche actif dans la physique des particules .

Modifié pour inclure les monopôles magnétiques

Les équations de Maxwell de l'électromagnétisme concernent les champs électriques et magnétiques aux mouvements de charges électriques. La forme standard des équations pour fournir une charge électrique, mais postulent aucune charge magnétique. Il n'y a pas analogique magnétique connu d'un électron, mais récemment, les scientifiques ont décrit le comportement dans un état cristallin de la matière connue comme spin-glace qui ont un comportement macroscopique comme monopôles magnétiques. (En accord avec le fait que la charge magnétique n'a jamais été vu et peut ne pas exister). Sauf pour cela, les équations sont symétriques en vertu échange de champ électrique et magnétique. En fait, des équations symétriques peuvent être écrites lorsque tous les frais sont à zéro, ce qui est la façon dont l' équation d'onde est dérivé (voir immédiatement ci-dessus).

Entièrement équations symétriques peuvent aussi être écrites si l'on permet la possibilité de charges magnétiques. Avec l'inclusion d'une variable pour ces charges magnétiques, dites ρ _m , il y aura également un "courant magnétique" variables dans les équations, J _m . Les équations de Maxwell étendues (en unités CGS de Gauss) sont comme suit:

Nom	Sans monopôles magnétiques	Avec monopôles magnétiques (hypothétique)
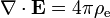
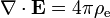
La loi de Gauss:	$\nabla \cdot \mathbf{E} = 4 \pi \rho_\mathrm{e}$	$\nabla \cdot \mathbf{E} = 4 \pi \rho_\mathrm{e}$
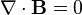
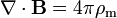
La loi de Gauss pour le magnétisme:	$\ Nabla \ cdot \ mathbf {B} = 0$	$\nabla \cdot \mathbf{B} = 4 \pi \rho_\mathrm{m}$
Équation de Maxwell-Faraday ( La loi de Faraday de l'induction):	$-\nabla \times \mathbf{E} = \frac{\partial \mathbf{B}} {\partial t}$	$-\nabla \times \mathbf{E} = \frac{\partial \mathbf{B}}{\partial t} + 4 \pi \mathbf{j}_\mathrm{m}$
La loi d'Ampère (Avec l'extension de Maxwell):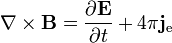	$\nabla \times \mathbf{B} = \frac{\partial \mathbf{E}} {\partial t} + 4 \pi \mathbf{j}_\mathrm{e}$	Dans certains cas, comme des guides d'ondes ou de la cavité des résonateurs, la région de la solution est en grande partie isolé à partir de l'univers, par exemple, par des parois métalliques, et les conditions aux limites sur les parois définissent les domaines de l'influence du monde extérieur confiné aux extrémités d'entrée / sortie la structure. Dans d'autres cas, l'univers dans son ensemble est parfois approchée par une frontière artificielle absorbant, ou, par exemple pour émettre des antennes ou des satellites de communication, ces conditions aux limites peuvent prendre la forme de limites asymptotiques imposées à la solution. En outre, par exemple dans une fibre optique ou à film mince optique, la région de la solution est souvent divisée en sous-régions avec leurs propres propriétés simplifiées, et les solutions dans chaque sous-région doit être joint à l'autre à travers les interfaces de sous-région à l'aide de conditions aux limites. Un exemple particulier de cette utilisation de conditions aux limites est le remplacement d'un matériau à polarisation de volume d'une couche de surface chargée, ou d'un matériau ayant une aimantation de volume par un courant de surface, comme décrit dans la section Bound charge et de courant . Voici quelques liens de nature générale concernant les problèmes de valeur limite: exemples de problèmes aux limites, la théorie de Sturm-Liouville, Dirichlet condition limite, Neumann condition limite, état limite mixte, Cauchy condition limite, Sommerfeld état de rayonnement. Inutile de dire, il faut choisir les conditions aux limites appropriées au problème est résolu. Voir aussi Kempel et le livre par Friedman. Unités de Gauss Unités de Gauss est un populaire variante de l'électromagnétisme de la deuxième système d'unités (CGS) centimètre de gramme. Dans les unités de gaussiennes, les équations de Maxwell sont: $\nabla \cdot \mathbf{D} = 4\pi\rho_\mathrm{f}$ $\ Nabla \ cdot \ mathbf {B} = 0$ $\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}} {\partial t}$ $\nabla \times \mathbf{H} = \frac{1}{c} \frac{\partial \mathbf{D}} {\partial t} + \frac{4\pi}{c} \mathbf{J}_\mathrm{f}$ où c est la vitesse de la lumière dans le vide. Les équations microscopiques sont: $\nabla \cdot \mathbf{E} = 4\pi\rho_{\mathrm{tot}}$ $\ Nabla \ cdot \ mathbf {B} = 0$ $\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}} {\partial t}$ $\nabla \times \mathbf{B} = \frac{1}{c} \frac{\partial \mathbf{E}}{\partial t} + \frac{4\pi}{c}\mathbf{J}_{\mathrm{tot}}.$ La relation entrechamp de déplacement électrique,champ électriqueetla densité de polarisation est: $\mathbf{D} = \mathbf{E} + 4\pi\mathbf{P}.$ Et de même la relation entre l'induction magnétique,champ magnétique et totaleaimantation est: $\mathbf{B} = \mathbf{H} + 4\pi\mathbf{M}.$ Dans l'approximation linéaire, lasusceptibilité électrique etsusceptibilité magnétique sont définis de telle sorte que: 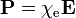$\mathbf{P} = \chi_\mathrm{e} \mathbf{E}$ , $\mathbf{M} = \chi_\mathrm{m} \mathbf{H}.$ (Note:. 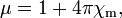Bien que les susceptibilités sont des nombres sans dimension dans les deux cgs et SI, ils diffèrent par la valeur d'un facteur de 4π) La permittivité et perméabilité sont: $\ \epsilon = 1+4\pi\chi_\mathrm{e}$ , $\ \mu = 1+4\pi\chi_\mathrm{m},$ de sorte que $\mathbf{D} = \epsilon \mathbf{E}$ , $\mathbf{B} = \mu \mathbf{H}.$ Dans le vide,ε=μ= 1, doncD=E, etB=H. La force exercée sur une particule chargée par lechamp électriqueetun champ magnétique est donnée par l'équation de la force de Lorentz: $\mathbf{F} = q \left(\mathbf{E} + \frac{\mathbf{v}}{c} \times \mathbf{B}\right),$ où q est la charge de la particule, et v est la vitesse des particules. Ce qui est légèrement différent de l' expression unité SI-dessus. Par exemple, le champ magnétique B a les mêmes unités que le champ électrique E . Quelques équations dans l'article sont donnés en unités de Gauss mais pas SI ou vice-versa. Heureusement, il existe des règles générales pour convertir de l'un à l'autre; Voir l'article unités de Gauss pour plus de détails. D'autres formulations des équations de Maxwell La relativité spéciale motivé une formulation mathématique compacte des équations de Maxwell, en termes detenseurs covariants.La mécanique quantiquea également motivé d'autres formulations. Par exemple, considérons un conducteur se déplaçant dans le champ d'un aimant. Dans le trame de l'aimant, ce conducteur éprouve un magnétique vigueur. Mais dans le cadre d'un conducteur se déplaçant par rapport à l'aimant, le conducteur subit une force due à une électrique champ. La formulation suivante montre comment les équations de Maxwell prennent la même forme dans tout système inertiel de coordonnées. Formulation covariante des équations de Maxwell Dans la relativité restreinte, afin d'exprimer plus clairement le fait que les équations de Maxwell («microscopiques») prennent la même forme dans tout système de coordonnées inertiel, les équations de Maxwell sont écrits en termes de quatre vecteurs et tenseurs dans le «manifestement sous forme covariante ". Les composants purement spatiales de la suivante sont en Unités SI. Un ingrédient dans cette formulation est letenseur électromagnétique, un covariant antisymétrique de rang 2tenseur combinant les champs électriques et magnétiques: $F_{\alpha \beta} = \left( \begin{matrix} 0 & \frac{-E_\mathrm{x}}{c} & \frac{-E_\mathrm{y}}{c} & \frac{-E_\mathrm{z}}{c} \\ \frac{E_\mathrm{x}}{c} & 0 & B_\mathrm{z} & -B_\mathrm{y} \\ \frac{E_\mathrm{y}}{c} & -B_\mathrm{z} & 0 & B_\mathrm{x} \\ \frac{E_\mathrm{z}}{c} & B_\mathrm{y} & -B_\mathrm{x} & 0 \end{matrix} \right)$ et le résultat de l'élévation ses indices $F^{\mu \nu} \, \stackrel{\mathrm{def}}{=} \, \eta^{\mu \alpha} \, F_{\alpha \beta} \, \eta^{\beta \nu} = \left( \begin{matrix} 0 & \frac{E_\mathrm{x}}{c} & \frac{E_\mathrm{y}}{c} & \frac{E_\mathrm{z}}{c} \\ \frac{-E_\mathrm{x}}{c} & 0 & B_\mathrm{z} & -B_\mathrm{y} \\ \frac{-E_\mathrm{y}}{c} & -B_\mathrm{z} & 0 & B_\mathrm{x} \\ \frac{-E_\mathrm{z}}{c} & B_\mathrm{y} & -B_\mathrm{x} & 0 \end{matrix} \right).$ L'autre ingrédient est lequatre-courant: $J^{\alpha} = (c\rho,\vec{J})$ oùρest ladensité de charge etJest ladensité de courant. Avec ces ingrédients, les équations de Maxwell peuvent être écrites: $\mu_{0} \, J^{\beta} \, = \, {\partial F^{\beta\alpha} \over {\partial x^{\alpha}} } \, \stackrel{\mathrm{def}}{=} \, \partial_{\alpha} F^{\beta\alpha} \, \stackrel{\mathrm{def}}{=} \, {F^{\beta\alpha}}_{,\alpha} \,$ et $0 = \partial_{\gamma} F_{\alpha\beta} + \partial_{\beta} F_{\gamma\alpha} + \partial_{\alpha} F_{\beta\gamma} \ \stackrel{\mathrm{def}}{=}\ {F_{\alpha\beta}}_{,\gamma} + {F_{\gamma\alpha}}_{,\beta} +{F_{\beta\gamma}}_{,\alpha}.$ La première équation de tenseur est une expression des deux équations de Maxwell non homogènes, la loi de Gauss et la loi d'Ampère avec correction de Maxwell. La seconde équation est une expression des deux équations homogènes, la loi de Faraday de l'induction et la loi de Gauss pour le magnétisme. La deuxième équation est équivalente à $0 = \epsilon^{\delta\alpha\beta\gamma} {F_{\beta\gamma}}_{,\alpha}$ où $\, \epsilon^{\alpha\beta\gamma\delta}$ est la version contravariant dusymbole de Levi-Civita, et ${ \partial \over { \partial x^{\alpha} } } \ \stackrel{\mathrm{def}}{=}\ \partial_{\alpha} \ \stackrel{\mathrm{def}}{=}\ {}_{,\alpha} \ \stackrel{\mathrm{def}}{=}\ \left(\frac{1}{c}\frac{\partial}{\partial t}, \nabla\right)$ est le 4-gradient. Dans les équations de tenseurs ci-dessus, les indices répétés sont additionnées selon Einstein convention de sommation. Nous avons affiché les résultats dans plusieurs notations communes. Haut-composants de plus bas et d'un vecteur, v ^α et v ^α respectivement, sont échangés avec le tenseur fondamental g , par exemple g = η = diag (1, 1, 1, 1). Présentations covariantes alternatifs des équations de Maxwell existent aussi, par exemple en termes dequatre potentiel; voir formulation covariante de l'électromagnétisme classique pour plus de détails. Formulation en potentiel En mécanique classique avancés et en mécanique quantique (où il est nécessaire), il est parfois utile d'exprimer les équations de Maxwell dans un «formulation potentiel» impliquant le potentiel électrique (aussi appelé potentiel scalaire), φ , et le potentiel magnétique, A , (également appelé potentiel vecteur). Ceux-ci sont définis de telle sorte que: $\mathbf E = - \mathbf \nabla \varphi - \frac{\partial \mathbf A}{\partial t},$ $\mathbf B = \mathbf \nabla \times \mathbf A.$ Avec ces définitions, les deux équations de Maxwell homogènes (loi de Faraday et la loi de Gauss pour le magnétisme) sont automatiquement remplies et que les deux autres équations (non homogènes) donnent les équations suivantes (pour "équations de Maxwell microscopiques»): $\nabla^2 \varphi + \frac{\partial}{\partial t} \left ( \mathbf \nabla \cdot \mathbf A \right ) = - \frac{\rho}{\varepsilon_0}$ $\left ( \nabla^2 \mathbf A - \frac{1}{c^2} \frac{\partial^2 \mathbf A}{\partial t^2} \right ) - \mathbf \nabla \left ( \mathbf \nabla \cdot \mathbf A + \frac{1}{c^2} \frac{\partial \varphi}{\partial t} \right ) = - \mu_0 \mathbf J.$ Ces équations, prises ensemble, sont aussi puissants et complets que les équations de Maxwell. En outre, si nous ne travaillons qu'avec les potentiels et d'ignorer les champs, le problème a été quelque peu réduite, que les champs électriques et magnétiques ont chacun trois composants qui doivent être résolus pour (six composants au total), tandis que les potentiels électriques et magnétiques ont seulement quatre composants ensemble. De nombreux choix différents de A et φ sont en accord avec une donnée E et B , ce qui rend ces choix physiquement équivalent - une flexibilité connu comme la liberté de la jauge. Choix approprié de A et φ peut simplifier ces équations, ou peut les adapter à une situation particulière. Quatre possibilités Dans le Jauge de Lorentz, les deux équations qui représentent les potentiels peut être réduite à une manifestementéquation invariante de Lorentz, l'utilisationdes quatre vecteurs: lequatre-courant défini par $j^\mu = \left( \rho c, \mathbf{j} \right)$ formé à partir de la densité de courantjet la charge de la densité ρ, et lequatre-potentiel électromagnétique définie par $A^\mu = \left( \varphi , \mathbf{A} c \right)$ formé à partir du potentiel vecteurAet le potentiel scalaire 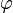$\varphi \,$ .L'équation unique résultant, en raison deArnold Sommerfeld, une généralisation d'une équation en raison deBernhard Riemannet connu comme l'équation de Riemann-Sommerfeld ou la forme covariante des équations de Maxwell, est: $\Box A^\mu = \mu_0 j^\mu$ , où $\Box=\partial^2=\partial_\alpha\partial^\alpha$ est le opérateur d'Alembertien, ou quatre Laplace, $\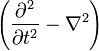left( {\partial^2 \over \partial t^2} - \nabla^2 \right)$ parfois écrites 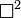$\ Box ^ 2$ Ou $\Box \cdot \Box$ Où $\Box$ est le de quatre dégradé. formulations de différentielles En espace libre, où ε = ε ₀ et μ = μ ₀ sont constants partout, les équations de Maxwell simplifier considérablement une fois que le langage de la géométrie différentielle et formes différentielles est utilisé. Dans ce qui suit, les unités CGS de Gauss, pas les unités SI sont utilisés. (Pour convertir à SI, voir ici.) Les champs électriques et magnétiques sont maintenant décrits conjointement par un 2-forme F dans un 4-dimensionnelle collecteur espace-temps. Les équations de Maxwell réduisent alors à l' identité de Bianchi $\mathrm{d}\bold{F}=0$ où d désigne ladérivée extérieure - coordonner un cadre naturel et opérateur différentiel métrique indépendante agissant sur les formes - et l'équation de la source $\mathrm {d} * {\bold{F}}=\bold{J}$ où le (bi)Hodge opérateur étoile * est une transformation linéaire à partir de l'espace de deux formes dans l'espace de (2.4) -Formulaires défini par la métrique dansl'espace de Minkowski (en quatre dimensions, même par une métriqueconforme à cette métrique ), et les champs sont enunités naturelles où 1 / 4pe ₀= 1. Ici, le 3-formeJest appelée laforme de courant électriqueou du courant 3-formesatisfaisant laéquation de continuité $\mathrm{d}{\bold{J}}=0.$ Le 3-forme actuelle peut être intégré sur une région en 3 dimensions d'espace-temps. L'interprétation physique de cette intégrale est la charge dans cette région si elle est de type espace, ou la quantité de charge qui circule à travers une surface dans un certain laps de temps si cette région est une surface de type espace traverser un intervalle de type temps. Comme dérivé extérieur est défini sur un collecteur , la version de la forme différentielle de l'identité de Bianchi logique pour chaque collecteur 4 dimensions, tandis que l'équation de source est défini si le collecteur est orienté et a une métrique de Lorentz. En particulier la version de forme différentielle des équations de Maxwell sont une formulation pratique et intuitive des équations de Maxwell en relativité générale. Dans un linéaire, théorie macroscopique, l'influence de la matière sur le champ électromagnétique est décrite par la transformation linéaire plus générale dans l'espace de deux formes. Nous appelons $C:\Lambda^2\ni\bold{F}\mapsto \bold{G}\in\Lambda^{(4-2)}$ la transformation constitutive. Le rôle de cette transformation est comparable à la transformation de la dualité de Hodge. Les équations de Maxwell dans la présence de la matière deviennent alors: $\mathrm{d}\bold{F} = 0$ $\mathrm{d}\bold{G} = \bold{J}$ où le 3-forme actuelleJrépond encore la continuité équation dJ= 0. Lorsque les champs sont exprimées comme des combinaisons linéaires (deproduits extérieurs) de base formulairesθ^p, $\bold{F} = \frac{1}{2}F_{pq}\bold{\theta}^p\wedge\bold{\theta}^q.$ la relation constitutive prend la forme $G_{pq} = C_{pq}^{mn}F_{mn}$ où les fonctions de coefficients de domaine sont antisymétrique des indices et des coefficients constitutifs sont antisymétrique dans les paires correspondantes. En particulier, la dualité de Hodge transformation conduisant à des équations de vide décrites ci-dessus sont obtenus en prenant $C_{pq}^{mn} = \frac{1}{2}g^{ma}g^{nb} \epsilon_{abpq} \sqrt{-g}$ qui jusqu'à mise à l'échelle est le seul tenseur invariant de ce type qui peut être défini avec la métrique. Dans cette formulation, l'électromagnétisme généralise immédiatement l'une tubulure orientée quatre dimensions ou de petites adaptations tout collecteur, ce qui nécessite même pas une métrique. Ainsi l'expression des équations de Maxwell en termes de formes différentielles conduit à une plus grande simplification de notation et conceptuel. Alors que les équations de Maxwell pourraient être écrites comme deux équations tensorielles au lieu de huit équations scalaires, à partir de laquelle la propagation de perturbations électromagnétiques et de l'équation de continuité pourrait être dérivé avec un peu d'effort, en utilisant des formes différentielles conduit à une dérivation encore plus simple de ces résultats. Compréhension conceptuelle de cette formulation Sur le plan conceptuel, du point de vue de la physique, ce qui montre que les deuxième et troisième équations de Maxwell devraient être regroupés, être appelé ceux homogènes, et être considérés comme des géométrique identités exprimant rien d'autre que: le champ F dérive d'un plus "fondamentale" potentiel A . Alors que le premier et le dernier devrait être considéré comme les dynamique équations du mouvement , obtenus via le principe de Lagrange de la moindre action, depuis le "terme d'interaction" AJ (introduit par jauge dérivées covariantes), couplant le champ à la matière. Souvent, le dérivé de temps dans la troisième loi motive l'appel de cette équation "dynamique", qui est quelque peu trompeur; dans le sens de l'analyse qui précède, cela est plutôt un artefact de rupture relativiste covariance en choisissant une direction de temps préféré. Pour avoir des degrés de liberté physiques propagée par ces équations de champ, il faut inclure un terme cinétique *F F pour A ; et prennent en compte les degrés non-physiques de liberté qui peuvent être éliminés par transformation de jauge A → A ' = A -. dα Voir également jauger fixation et Faddeev-Popov fantômes. Geometric Algebra (GA) formulation En algèbre géométrique, les équations de Maxwell sont réduites à une seule équation, $\left(\frac{1}{c}\partial_t + \boldsymbol{\nabla}\right)F = \mu_0 c J,$ oùFetJsont multivecteurs $F = \bold{E} + Ic\bold{B}$ et $J = c \rho + \bold{J}.$ avec l'unitépseudoscalaireI ²= -1 L'opérateur gradient spatial GA∇agit sur un champ de vecteurs, de telle sorte que $\boldsymbol{\nabla}\bold{F} = \boldsymbol{\nabla} \cdot \bold{F} + I \boldsymbol{\nabla} \times \bold{F},$ En algèbre de l'espace-temps en utilisant le même produit l'équation géométrique est simplement $\nabla F = \mu_0 c J,$ le dérivé de l'espace-temps du champ électromagnétique est la source. Voici le (non gras) gradient de l'espace-temps $\nabla = \gamma^\mu \partial_\mu$ est un vecteur de quatre, de même que la densité de courant $J = \gamma_{\mu} J^{\mu} = \gamma_0 c \rho + J^k \gamma_k = (c \rho + \bold{J})\gamma_0.$ Pour une démonstration que les équations données reproduisent les équations de Maxwell voir l'article principal. L'électrodynamique classique que la courbure d'un faisceau de ligne Une manière élégante et intuitive pour formuler les équations de Maxwell est d'utiliser complexes fibrés ou fibrés principaux avec de la fibre U (1). Le lien $\ Nabla$ sur le faisceau de la ligne a une courbure $\bold{F} = \nabla^2$ qui est un deux-forme automatiquement satisfait $\mathrm{d}\bold{F} = 0$ et peuvent être interprétées comme une intensité de champ . Si le faisceau de la ligne est trivial en référence plat connexion d , nous pouvons écrire $\nabla = \mathrm{d}+\bold{A}$ et F = d A avec A la 1-forme composée du potentiel électrique et le potentiel vecteur magnétique. En mécanique quantique, la connexion elle-même est utilisée pour définir la dynamique du système. Cette formulation permet une description naturelle de l' effet Aharonov-Bohm. Dans cette expérience, un champ magnétique statique traverse un fil magnétique longue (par exemple, un fil de fer magnétisé longitudinalement). En dehors de ce fil l'induction magnétique est égal à zéro, à la différence du potentiel vecteur, qui dépend essentiellement du flux magnétique à travers la section transversale du fil et qui ne disparaît pas à l'extérieur. Comme il n'y a pas de champ électrique soit, le tenseur de Maxwell F = 0** dans toute la région d'espace-temps à l'extérieur du tube, pendant l'expérience. Cela signifie par définition que la connexion $\ Nabla$ est plat il. Cependant, comme mentionné, la liaison dépend du champ magnétique à travers le tube depuis la holonomie long d'une courbe non-contractile qui entoure le tube est le flux magnétique à travers le tube dans les unités appropriées. Ceci peut être détecté quantique mécanique avec une expérience de diffraction d'électrons à double fente sur une vague d'électrons voyageant autour du tube. Le holonomie correspond à un décalage de phase supplémentaire, ce qui conduit à un changement dans le motif de diffraction. Espace courbe Formulation traditionnelle La matière et l'énergie génèrent courbure de l'espace-temps. ce fait l'objet de la relativité générale . Courbure de l'espace-temps affecte l'électrodynamique. Un champ électromagnétique ayant une énergie et l'élan génère également courbure dans l'espace-temps. Les équations de Maxwell dans l'espace-temps courbe peuvent être obtenus en remplaçant les dérivés dans les équations dans l'espace-temps plat avec dérivées covariantes. Les équations provenant de source et libre-deviennent ((Que ce soit la généralisation appropriée exige une enquête séparée.) unités CGS de Gauss): ${ 4 \pi \over c }j^{\beta} = \partial_{\alpha} F^{\alpha\beta} + {\Gamma^{\alpha}}_{\mu\alpha} F^{\mu\beta} + {\Gamma^{\beta}}_{\mu\alpha} F^{\alpha \mu} \ \stackrel{\mathrm{def}}{=}\ D_{\alpha} F^{\alpha\beta} \ \stackrel{\mathrm{def}}{=}\ {F^{\alpha\beta}}_{;\alpha} \, \!$ et $0 = \partial_{\gamma} F_{\alpha\beta} + \partial_{\beta} F_{\gamma\alpha} + \partial_{\alpha} F_{\beta\gamma} = D_{\gamma} F_{\alpha\beta} + D_{\beta} F_{\gamma\alpha} + D_{\alpha} F_{\beta\gamma}.\,$ Ici, ${\Gamma^{\alpha}}_{\mu\beta} \!$ est un Christoffel symbole qui caractérise la courbure de l'espace-temps etD_γest la dérivée covariante. Formulation en termes de formes différentielles La formulation des équations de Maxwell en termes de formes différentielles peut être utilisé sans changement de la relativité générale. L'équivalence de la formulation relativiste général plus traditionnel en utilisant la dérivée covariante avec la formulation de la forme différentielle peut être considérée comme suit. Choisissez coordonnées locales x ^α qui donne une base de 1-formes d x ^α dans chaque point de l'ouvert où les coordonnées sont définies. En utilisant cette base et unités CGS de Gauss nous définissons Le tenseur de champ infinitésimal antisymétrique 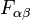$F_{\alpha\beta}$ , correspondant au champ 2-formeF $\bold{F} := \frac{1}{2}F_{\alpha\beta} \,\mathrm{d}\,x^{\alpha} \wedge \mathrm{d}\,x^{\beta}.$ Le courant-vecteur infinitésimal 3-formeJ $\bold{J} := {4 \pi \over c } j^{\alpha} \sqrt{-g} \, \epsilon_{\alpha\beta\gamma\delta} \mathrm{d}\,x^{\beta} \wedge \mathrm{d}\,x^{\gamma} \wedge \mathrm{d}\,x^{\delta}.$ Icigest comme d'habitude le déterminant de la métrique 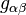$g_{\alpha\beta}$ .Un petit calcul qui utilise la symétrie dessymboles de Christoffel (ie, la torsion-liberté de laconnexion de Levi Civita) et la transmission permanente covariante de l'opérateur étoiles Hodge montre ensuite que, dans cette coordonnée quartier, nous avons: l'identité de Bianchi $\mathrm{d}\bold{F} = 2(\partial_{\gamma} F_{\alpha\beta} + \partial_{\beta} F_{\gamma\alpha} + \partial_{\alpha} F_{\beta\gamma})\mathrm{d}\,x^{\alpha}\wedge \mathrm{d}\,x^{\beta} \wedge \mathrm{d}\,x^{\gamma} = 0,$ l'équation de la source $\mathrm{d} * \bold{F} = {F^{\alpha\beta}}_{;\alpha}\sqrt{-g} \, \epsilon_{\beta\gamma\delta\eta}\mathrm{d}\,x^{\gamma} \wedge \mathrm{d}\,x^{\delta} \wedge \mathrm{d}\,x^{\eta} = \bold{J},$ l'équation de continuité $\mathrm{d}\bold{J} = { 4 \pi \over c } {j^{\alpha}}_{;\alpha} \sqrt{-g} \, \epsilon_{\alpha\beta\gamma\delta}\mathrm{d}\,x^{\alpha}\wedge \mathrm{d}\,x^{\beta} \wedge \mathrm{d}\,x^{\gamma} \wedge \mathrm{d}\,x^{\delta} = 0.$