
Interpolation
À propos de ce écoles sélection Wikipedia
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
Dans le mathématique de la sous-zone analyse numérique, l'interpolation est un procédé de construction de nouveaux points de données dans la plage de un ensemble discret de points de données connus.
Dans l'ingénierie et de la science on a souvent un certain nombre de points de données, obtenue par échantillonnage ou expérience, et tente de construire une fonction qui se adapte étroitement ces points de données. Cela se appelle courbe d'ajustement ou de l'analyse de régression . L'interpolation est un cas particulier de montage de la courbe, dans lequel la fonction doit aller exactement par les points de données.
Un autre problème qui est étroitement liée à l'interpolation est l'approximation d'une fonction compliquée par une fonction simple. Supposons que nous savons la fonction mais il est trop complexe à évaluer efficacement. Ensuite, nous pourrions prendre quelques points de données connues de la fonction compliquée, la création d'un Table de consultation, et essayer d'interpoler les points de données pour construire une fonction simple. Bien sûr, lorsque vous utilisez la fonction simple à calculer de nouveaux points de données nous avons l'habitude ne recevons pas le même résultat que lors de l'utilisation de la fonction d'origine, mais en fonction du domaine de problème et la méthode d'interpolation utilisés le gain dans la simplicité pourrait compenser l'erreur.
Il convient de mentionner qu'il existe un autre type très différent de l'interpolation en mathématiques, à savoir la " interpolation des opérateurs ". Les résultats classiques sur interpolation des opérateurs sont les Théorème de Riesz-Thorin et Théorème Marcinkiewicz. Il ya aussi beaucoup d'autres résultats ultérieurs.
Définition
De inter sens entre et le pôle, les points ou nœuds. Tout moyen de calculer un nouveau point entre deux points de données existantes est donc interpolation.
Il existe de nombreuses méthodes pour ce faire, dont beaucoup impliquent montage une sorte de fonction pour les données et l'évaluation de cette fonction au point désiré. Cela ne exclut pas d'autres moyens tels que des méthodes statistiques de calcul de données interpolées.
La forme la plus simple d'interpolation consiste à prendre la moyenne arithmétique des 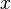 et
et  de deux points adjacents pour trouver le point à mi. Cela donnera le même résultat que l'interpolation linéaire évaluée au point milieu.
de deux points adjacents pour trouver le point à mi. Cela donnera le même résultat que l'interpolation linéaire évaluée au point milieu.
Compte tenu d'une séquence de n nombres distincts x k appelés nœuds et pour chaque x k un second nombre y k, nous sommes à la recherche d'une fonction f sorte que
Une paire x k, y k est appelé un point de données et f est appelé un interpolant les points de données.
Lorsque le nombre k y sont donnés par une fonction connue f, nous écrivons parfois f k.
Exemple
Par exemple, supposons que nous ayons un tableau comme celui qui donne des valeurs d'une fonction inconnue f.

| x | f (x) | ||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 1 | 0 | . | 8415 | ||
| 2 | 0 | . | 9093 | ||
| 3 | 0 | . | 1411 | ||
| 4 | -0 | . | 7568 | ||
| 5 | -0 | . | 9589 | ||
| 6 | -0 | . | 2794 | ||
Interpolation fournit un moyen d'estimation de la fonction aux points intermédiaires, telles que x = 2,5.
Il existe de nombreuses méthodes d'interpolation différentes, dont certaines sont décrites ci-dessous. Certaines des préoccupations à prendre en compte lors du choix d'un lieu algorithme sont: Quelle est la précision de la méthode? Quel est le coût? Comment lisse est l'interpolant? Combien de points de données sont nécessaires?
Interpolation constante par morceaux
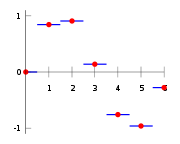
La méthode d'interpolation la plus simple est de localiser la valeur de données le plus proche, et attribuer la même valeur. Dans une dimension, il ya rarement de bonnes raisons de choisir celui sur interpolation linéaire, qui est presque aussi pas cher, mais dans des dimensions plus élevées, dans interpolation multivariée, cela peut être un choix favorable pour sa rapidité et simplicité.
Interpolation linéaire

Une des méthodes les plus simples est interpolation linéaire (parfois connu sous le nom lerp). Prenons l'exemple ci-dessus de détermination de f (2,5). Depuis 2.5 est à mi-chemin entre 2 et 3, il est raisonnable de prendre f (2,5) mi-chemin entre f (2) = 0,9093 et f (3) = 0,1411, ce qui donne 0,5252.
En général, une interpolation linéaire prend deux points de données, par exemple (x a, y a) et (x b, y b), et l'interpolant est donnée par:
 au point (x, y).
au point (x, y).
Interpolation linéaire est rapide et facile, mais il ne est pas très précis. Un autre inconvénient est que l'interpolant ne est pas dérivable au point x k.
L'estimation d'erreur suivant montre que l'interpolation linéaire ne est pas très précis. Notons la fonction que nous voulons pour interpoler par g, et supposons que x se situe entre x et x un b et g est deux fois continûment différentiable. Ensuite, l'erreur d'interpolation linéaire est
En termes, l'erreur est proportionnelle au carré de la distance entre les points de données. L'erreur de certaines autres méthodes, y compris l'interpolation polynomiale et interpolation spline (décrit ci-dessous), est proportionnelle à des puissances plus élevées de la distance entre les points de données. Ces méthodes produisent également interpolants lisses.
Interpolation polynomiale
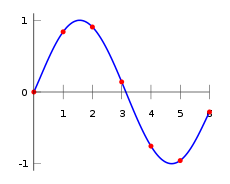
Interpolation polynomiale est une généralisation de l'interpolation linéaire. Notez que l'interpolant linéaire est un fonction linéaire. Nous remplaçons maintenant ce interpolant par un polynôme du supérieur degré.
Considérons à nouveau le problème ci-dessus. La sixième polynôme de degré à la suite passe par toutes les sept points:
En substituant x = 2.5, nous constatons que f (2,5) = 0,5965.
En général, si on a n points de données, il est tout à fait une polynôme de degré au plus n-1 en passant par tous les points de données. L'erreur d'interpolation est proportionnelle à la distance entre les points de données à la puissance n. En outre, l'interpolant est un polynôme et donc infiniment différentiables. Donc, on voit que l'interpolation polynomiale permet de résoudre tous les problèmes d'interpolation linéaire.
Cependant, l'interpolation polynomiale a aussi quelques inconvénients. Le calcul du polynôme d'interpolation est relativement très coûteux en calcul (voir complexité de calcul). En outre, l'interpolation polynomiale peut ne pas être si exact après tout, notamment au niveau des points d'extrémité (voir Phénomène de Runge). Ces inconvénients peuvent être évités en utilisant une interpolation spline.
Interpolation Spline

Rappelez-vous que interpolation linéaire utilise une fonction linéaire pour chacun des intervalles [x k, k x + 1]. Interpolation Spline utilise des polynômes de bas degré dans chacun des intervalles, et choisit les morceaux de polynômes de telle sorte qu'ils se adaptent sans problème ensemble. La fonction résulte est appelé spline.
Par exemple, le spline cubique naturelle est morceaux cube et deux fois continûment différentiable. En outre, sa dérivée seconde est égale à zéro au niveau des points d'extrémité. Le spline cubique naturelle interpoler les points dans le tableau ci-dessus est donnée par
Dans ce cas, nous obtenons f (2,5) = 0,597262.
Comme l'interpolation polynomiale, interpolation spline encourt une erreur inférieure à interpolation linéaire et l'interpolant est plus lisse. Cependant, l'interpolant est plus facile à évaluer que les polynômes-degré élevé utilisés dans l'interpolation polynomiale. Elle ne souffre pas de Phénomène de Runge.
D'autres formes d'interpolation
D'autres formes d'interpolation peuvent être construites en choisissant une classe différente de interpolants. Par exemple, interpolation rationnelle est l'interpolation par fonctions rationnelles, et interpolation trigonométrique est par interpolation polynômes trigonométriques. La transformée de Fourier discrète est un cas particulier d'interpolation trigonométrique. Une autre possibilité consiste à utiliser ondelettes.
Le Formule d'interpolation de Whittaker-Shannon peut être utilisé si le nombre de points de données est infini.
Interpolation à plusieurs variables est l'interpolation des fonctions de plusieurs variables. Les méthodes comprennent interpolation bilinéaire et interpolation bicubique en deux dimensions, et interpolation trilinéaire en trois dimensions.
Parfois, nous savons non seulement la valeur de la fonction que nous voulons pour interpoler, à certains moments, mais aussi son dérivé. Cela conduit à Problèmes d'interpolation d'Hermite.
Concepts associés
Le terme extrapolation est utilisé si nous voulons trouver des points de données en dehors de la gamme de points de données connus.
En courbe des problèmes de montage, la contrainte que l'interpolant doit aller exactement par les points de données est détendue. Il est seulement nécessaire de se approcher des points de données le plus étroitement possible. Cela nécessite le paramétrage des interpolants potentiels et ayant un moyen de mesurer l'erreur. Dans le cas le plus simple ce qui conduit à moins carrés rapprochement.
Études de théorie de l'approximation comment trouver la meilleure approximation d'une fonction donnée par une autre fonction de certains classe prédéterminée, et comment cette approximation est bonne. Cela donne clairement un bond sur la façon dont l'interpolant peut se rapprocher de la fonction inconnue.
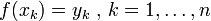
![| F (x) -g (x) | \ le C (X_B-x_a) ^ 2 \ quad \ mbox {} où \ quad C = \ frac18 \ max_ {y \ in [x_a, X_B]} | g '' (y) |.](../../images/71/7171.png)

![f (x) = \ \ \ {gauche begin {matrix} -0,1522 x ^ 3 + 0,9937 x, & \ mbox {if} x \ in [0,1], \\ -0,01258 x ^ 3 à 0,4189 x ^ 2 + 1,4126 x - 0,1396, et \ mbox {if} x \ in [1,2], \\ 0,1403 x ^ 3 à 1,3359 x ^ 2 + 3,2467 x - 1,3623, et \ mbox {if} x \ in [2, 3], \\ 0,1579 x ^ 3 à 1,4945 x ^ 2 + 3,7225 x - 1,8381, et \ mbox {if} x \ in [3,4], \\ 0,05375 x ^ 3 -0,2450 x ^ 2 à 1,2756 x + 4,8259, et \ mbox {if} x \ in [4,5], \\ -0,1871 x ^ 3 + 3,3673 x ^ 2 à 19,3370 34,9282 x +, & \ mbox {if} x \ in [5,6]. \\ \ End {matrix} \ right.](../../images/71/7182.png)
