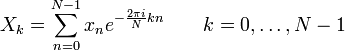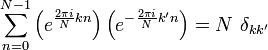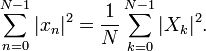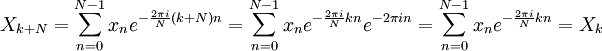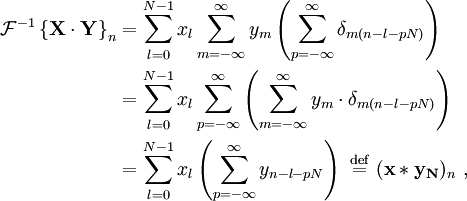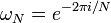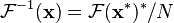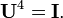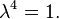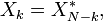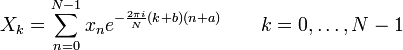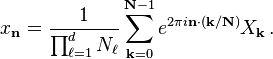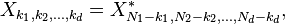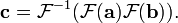Transformée de Fourier discrète
Contexte des écoles Wikipédia
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. Parrainer un enfant de faire une réelle différence.
| transformées de Fourier |
|---|
| Transformée de Fourier en continu |
| série de Fourier |
| Temps discret transformée de Fourier |
| Transformée de Fourier discrète |
En mathématiques , la transformée de Fourier discrète (DFT) est l'une des formes spécifiques de analyse de Fourier. En tant que tel, il se transforme en une autre fonction, qui est appelé le représentation dans le domaine fréquence, ou simplement la TFD, de la fonction d'origine (ce qui est souvent une fonction du dans le domaine temporel). Mais la DFT nécessite une fonction d'entrée qui est valeurs discrètes et dont les non-zéro ont une (finie) de durée limitée. Ces entrées sont souvent créées par échantillonnage d'une fonction continue, comme la voix d'une personne. Et, contrairement à la discret dans le temps à transformée de Fourier (DTFT), on évalue seulement assez de composantes de fréquence pour reconstruire le segment fini qui a été analysé. Sa transformée inverse ne peut pas reproduire le domaine temporel entière, à moins que l'entrée se trouve être périodique (toujours). Par conséquent, il est souvent dit que la DFT est une transformation pour l'analyse de Fourier des fonctions à temps discret finie domaine. Les fonctions de base de la décomposition sinusoïdales ont les mêmes propriétés.
Etant donné que la fonction d'entrée est une séquence finie de réels ou des nombres complexes , la TFD est idéal pour les informations de traitement stockées dans les ordinateurs . En particulier, la TFD est largement utilisé dans traitement du signal et des domaines connexes pour analyser les fréquences contenues dans une échantillonné signaler, pour résoudre des équations aux dérivées partielles et d'effectuer d'autres opérations telles que circonvolutions. La DFT peut être calculé de manière efficace dans la pratique en utilisant un transformée de Fourier rapide (FFT).
Depuis algorithmes FFT sont si couramment utilisées pour calculer la DFT, les deux termes sont souvent utilisés indifféremment dans des contextes familiers, bien qu'il y ait une distinction claire: "DFT" se réfère à une transformation mathématique, indépendamment de la façon dont il est calculé, tandis que "FFT" fait référence à un quelconque de plusieurs algorithmes efficaces pour la TFD. Cette distinction est plus floue, cependant, par le synonyme transformée de Fourier finie pour le DFT, qui précède apparemment le terme «transformée de Fourier rapide» (Cooley et al., 1969) mais a le même sigle.
Définition
La séquence de N nombres complexes x 0, ..., x N-1 est transformé en la séquence de N nombres complexes X 0, ..., X N-1 par la TFD d'après la formule:
où 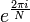 est un Nième primitive racine de l'unité.
est un Nième primitive racine de l'unité.
La transformation est parfois désigné par le symbole 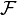 , Comme dans
, Comme dans  ou
ou  ou
ou 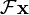 .
.
Le Fourier discrète inverse (IDFT) est donnée par
Une simple description de ces équations est que les nombres complexes  représenter l'amplitude et la phase des différents composantes sinusoïdales du "signal" d'entrée
représenter l'amplitude et la phase des différents composantes sinusoïdales du "signal" d'entrée  . La DFT calcule la
. La DFT calcule la  du
du  , Tandis que l'IDFT montre comment calculer le
, Tandis que l'IDFT montre comment calculer le  comme la somme des composantes sinusoïdales
comme la somme des composantes sinusoïdales 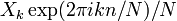 avec fréquence
avec fréquence 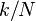 cycles par échantillon. En écrivant les équations sous cette forme, nous faisons un usage intensif des La formule d'Euler pour exprimer en termes de sinusoïdes exponentielles complexes, qui sont beaucoup plus faciles à manipuler. (De la même manière, par écrit
cycles par échantillon. En écrivant les équations sous cette forme, nous faisons un usage intensif des La formule d'Euler pour exprimer en termes de sinusoïdes exponentielles complexes, qui sont beaucoup plus faciles à manipuler. (De la même manière, par écrit  en forme polaire , on obtient immédiatement l'amplitude de sinusoïde
en forme polaire , on obtient immédiatement l'amplitude de sinusoïde 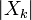 et la phase de la argumentation complexe.) Une subtilité importante de cette représentation, aliasing, est discutée ci-dessous.
et la phase de la argumentation complexe.) Une subtilité importante de cette représentation, aliasing, est discutée ci-dessous.
A noter que le facteur de normalisation et multiplier la transformée DFT IDFT (ici 1 et 1 / N) et les signes des exposants sont simplement conventions, et diffèrent dans certains traitements. Les seules exigences de ces conventions sont que la DFT et IDFT ont des exposants de signes opposés et que le produit de leurs facteurs de normalisation être 1 / N. Une normalisation de  à la fois pour la TFD et IDFT rend les transformations unitaire, ce qui présente certains avantages théoriques, mais il est souvent plus pratique de calcul numérique pour effectuer la mise à l'échelle en une seule fois comme ci-dessus (et une mise à l'échelle de l'unité peut être pratique d'une autre manière).
à la fois pour la TFD et IDFT rend les transformations unitaire, ce qui présente certains avantages théoriques, mais il est souvent plus pratique de calcul numérique pour effectuer la mise à l'échelle en une seule fois comme ci-dessus (et une mise à l'échelle de l'unité peut être pratique d'une autre manière).
(La convention d'un signe négatif dans l'exposant est souvent pratique car cela signifie que  est l'amplitude d'une "fréquence positif"
est l'amplitude d'une "fréquence positif" 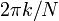 . Équivalente, la DFT est souvent considéré comme un Filtre adapté: lors de la recherche pour une fréquence de 1, une corrélation du signal entrant avec une fréquence de -1).
. Équivalente, la DFT est souvent considéré comme un Filtre adapté: lors de la recherche pour une fréquence de 1, une corrélation du signal entrant avec une fréquence de -1).
Dans la discussion qui suit les termes "séquence" et "vecteur" seront considérés comme interchangeables.
Propriétés
État complet
La transformée de Fourier discrète est une inversible, transformation linéaire
avec 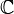 représentant l'ensemble des nombres complexes . En d'autres termes, pour tout n> 0, un vecteur de dimension N a un complexe DFT et une IDFT qui sont à leur tour N vecteurs complexes de dimension.
représentant l'ensemble des nombres complexes . En d'autres termes, pour tout n> 0, un vecteur de dimension N a un complexe DFT et une IDFT qui sont à leur tour N vecteurs complexes de dimension.
Orthogonalité
Les vecteurs  pour homme base orthogonale sur l'ensemble des vecteurs complexes de N:
pour homme base orthogonale sur l'ensemble des vecteurs complexes de N:
où  est le Kronecker. Cette condition d'orthogonalité peut être utilisée pour dériver la formule de l'IDFT de la définition de la TFD, et est équivalent à la propriété unitarity ci-dessous.
est le Kronecker. Cette condition d'orthogonalité peut être utilisée pour dériver la formule de l'IDFT de la définition de la TFD, et est équivalent à la propriété unitarity ci-dessous.
Le théorème de Plancherel et le théorème de Parseval
Si X et Y k k sont les TFD de x n et y n respectivement alors le Théorème de Plancherel états:
où l'étoile désigne conjugaison complexe. Égalité de Parseval est un cas particulier du théorème et les Etats Plancherel:
Ces théorèmes sont également équivalente à la condition unitaire ci-dessous.
Périodicité
Si l'expression qui définit la DFT est évaluée pour tous les entiers  au lieu de simplement pour
au lieu de simplement pour  , Alors la séquence infinie résultant est une extension périodique de la TFD, périodique de période N.
, Alors la séquence infinie résultant est une extension périodique de la TFD, périodique de période N.
La périodicité peut être démontré directement à partir de la définition:
où nous avons utilisé le fait que 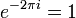 . De la même manière il peut être démontré que la formule IDFT conduit à une extension périodique.
. De la même manière il peut être démontré que la formule IDFT conduit à une extension périodique.
Le théorème de changement de vitesse
Multipliant  d'une phase linéaire
d'une phase linéaire  pour un certain entier
pour un certain entier  correspond à un décalage circulaire de la sortie
correspond à un décalage circulaire de la sortie  :
:  est remplacé par
est remplacé par  , Où l'indice est interprétée modulo
, Où l'indice est interprétée modulo 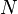 (Ce est-périodique). De même, un déplacement circulaire de l'entrée
(Ce est-périodique). De même, un déplacement circulaire de l'entrée  correspond à multiplier la sortie
correspond à multiplier la sortie  d'une phase linéaire. Mathématiquement, si
d'une phase linéaire. Mathématiquement, si 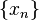 représente le vecteur x puis
représente le vecteur x puis
- si

- puis

- et

Circulaire théorème de convolution et de corrélation croisée théorème
Le théorème de convolution du temps continu et discret transformées de Fourier qui indique une convolution de deux séquences infinite peut être obtenue comme la transformée inverse du produit des transformations individuelles. Avec les séquences et les transformées de longueur n, a circularité se pose:
La quantité entre parenthèses est égal à 0 pour toutes les valeurs de  l'exception de ceux de la forme
l'exception de ceux de la forme  Où
Où 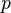 est un entier quelconque. Lors de ces valeurs, il est égal à 1. Il peut donc être remplacé par une somme infinie de Fonctions delta de Kronecker, et nous continuons en conséquence. Notez que nous pouvons également étendre les limites de
est un entier quelconque. Lors de ces valeurs, il est égal à 1. Il peut donc être remplacé par une somme infinie de Fonctions delta de Kronecker, et nous continuons en conséquence. Notez que nous pouvons également étendre les limites de  à l'infini, avec la compréhension que le
à l'infini, avec la compréhension que le 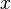 et
et  des séquences sont définis comme 0 en dehors de [0, N-1]:
des séquences sont définis comme 0 en dehors de [0, N-1]:
qui est la convolution de la 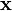 avec une séquence périodiquement étendu
avec une séquence périodiquement étendu 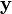 séquence définie par:
séquence définie par:
De même, il peut être montré que:
qui est le corrélation croisée de 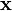 et
et 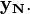
Une évaluation directe de la convolution ou de corrélation sommation, ci-dessus, nécessite 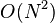 opérations. Une méthode indirecte, en utilisant des transformations, peut profiter de la
opérations. Une méthode indirecte, en utilisant des transformations, peut profiter de la  l'efficacité de la transformée de Fourier rapide (FFT) afin d'obtenir de bien meilleures performances. Par ailleurs, les circonvolutions peuvent être utilisés pour calculer efficacement par TFD L'algorithme FFT et de Rader L'algorithme FFT de Bluestein.
l'efficacité de la transformée de Fourier rapide (FFT) afin d'obtenir de bien meilleures performances. Par ailleurs, les circonvolutions peuvent être utilisés pour calculer efficacement par TFD L'algorithme FFT et de Rader L'algorithme FFT de Bluestein.
Méthodes ont également été développés pour utiliser convolution circulaire dans le cadre d'un processus efficace qui réalise normale (non circulaire) convolution avec un 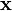 ou
ou 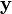 séquence potentiellement beaucoup plus longue que la taille transformer pratique (N). Deux de ces méthodes sont appelées chevaucher-enregistrer et empiètement additif.
séquence potentiellement beaucoup plus longue que la taille transformer pratique (N). Deux de ces méthodes sont appelées chevaucher-enregistrer et empiètement additif.
Trigonométrique interpolation polynomiale
Le trigonométrique interpolation polynomiale
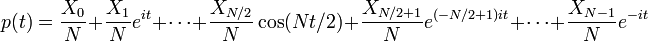 pour
pour 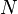 même,
même,  pour
pour  impair,
impair,
où les coefficients X k / N sont données par la transformée DFT x n ci-dessus, satisfait à la propriété d'interpolation  pour
pour 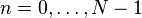 .
.
Pour encore 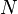 , Notez que la Composante de Nyquist
, Notez que la Composante de Nyquist 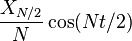 est traitée spécialement.
est traitée spécialement.
Cette interpolation est pas unique: aliasing implique que l'on peut ajouter à l'une quelconque des N fréquences de sinusoïde complexe (par exemple, changement  à
à  ) Sans changer la propriété d'interpolation, mais donnant des valeurs différentes entre le
) Sans changer la propriété d'interpolation, mais donnant des valeurs différentes entre le  Le secteur. Le choix ci-dessus, cependant, est typique parce qu'il a deux propriétés utiles. Tout d'abord, il se compose de sinusoïdes dont les fréquences ont la plus petite des amplitudes possibles, et donc minimise la moyenne quadratique pente
Le secteur. Le choix ci-dessus, cependant, est typique parce qu'il a deux propriétés utiles. Tout d'abord, il se compose de sinusoïdes dont les fréquences ont la plus petite des amplitudes possibles, et donc minimise la moyenne quadratique pente 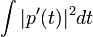 de la fonction d'interpolation. Deuxièmement, si le
de la fonction d'interpolation. Deuxièmement, si le  sont des nombres réels, puis
sont des nombres réels, puis  est réel ainsi.
est réel ainsi.
En revanche, la plus évidente trigonométrique interpolation polynomiale la est celui dans lequel les fréquences comprises entre 0 et  (Au lieu de plus ou moins
(Au lieu de plus ou moins  à
à 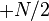 comme ci-dessus), similaire à la formule DFT inverse. Cette interpolation ne minimise pas la pente, et ne est généralement valeurs réelles pour de vrai
comme ci-dessus), similaire à la formule DFT inverse. Cette interpolation ne minimise pas la pente, et ne est généralement valeurs réelles pour de vrai  ; son utilisation est une erreur commune.
; son utilisation est une erreur commune.
Le DFT unitaire
Une autre façon de regarder le DFT est à noter que, dans la discussion ci-dessus, la DFT peut être exprimée comme une Vandermonde matrice:
où
est une primitive Racine nième de l'unité. La transformée inverse est alors donnée par l'inverse de la matrice ci-dessus:
Avec unitaires constantes de normalisation  , La DFT devient transformation unitaire, définie par une matrice unitaire:
, La DFT devient transformation unitaire, définie par une matrice unitaire:
où det () est le facteur déterminant fonction. Le déterminant est le produit des valeurs propres, qui sont toujours  ou
ou  comme décrit ci-dessous. Dans un espace vectoriel réel, une transformation unitaire peut être considérée comme une simple rotation rigide du système de coordonnées, et toutes les propriétés d'une rotation rigide peut être trouvée dans la DFT unitaire.
comme décrit ci-dessous. Dans un espace vectoriel réel, une transformation unitaire peut être considérée comme une simple rotation rigide du système de coordonnées, et toutes les propriétés d'une rotation rigide peut être trouvée dans la DFT unitaire.
L'orthogonalité de la TFD est maintenant exprimé en condition de orthonormalité (qui se pose dans de nombreux domaines des mathématiques comme décrit dans racine de l'unité):
Si  est défini comme la DFT du vecteur unitaire
est défini comme la DFT du vecteur unitaire 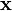 puis
puis
et le Plancherel théorème est exprimé comme suit:
Si nous considérons la DFT comme juste une transformation qui spécifie simplement les composantes d'un vecteur dans un nouveau système de coordonnées de coordonnées, le précède est juste la déclaration que le produit scalaire de deux vecteurs est conservé sous une transformation unitaire DFT. Pour le cas particulier 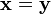 Ceci implique que la longueur d'un vecteur est conservé comme bien ce est juste De Parseval théorème:
Ceci implique que la longueur d'un vecteur est conservé comme bien ce est juste De Parseval théorème:
Exprimant le DFT inverse en termes de DFT
Une propriété utile de la TFD est que la TFD inverse peut être facilement exprimé en termes de (avant) DFT, via plusieurs «trucs» bien connus. (Par exemple, dans les calculs, il est souvent commode de mettre en oeuvre uniquement une transformée de Fourier rapide de transformée correspondant à une direction et ensuite pour obtenir la transformation autre direction à partir de la première).
Premièrement, nous pouvons calculer la DFT inverse en inversant les entrées:
(Comme d'habitude, les indices sont interprétés modulo 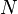 ; Ainsi, par
; Ainsi, par  , Nous avons
, Nous avons  .)
.)
Deuxièmement, on peut aussi conjuguer les entrées et les sorties:
Troisièmement, une variante de cette conjugaison tour, ce qui est parfois préférable car elle ne nécessite aucune modification des valeurs de données, comprend la permutation des parties réelles et imaginaires (qui peut être fait sur un ordinateur simplement en modifiant pointeurs). Définir swap (  ) Comme
) Comme  avec ses parties réelles et imaginaires permutées, ce est-si
avec ses parties réelles et imaginaires permutées, ce est-si  puis échanger (
puis échanger (  ) Est
) Est  . Équivalente, swap (
. Équivalente, swap (  ) Est égal
) Est égal  . Puis
. Puis
Autrement dit, la transformation inverse est la même que la transformée directe avec les parties réelles et imaginaires permutées pour l'entrée et la sortie, jusqu'à une normalisation (Duhamel et al., 1988).
L'astuce de conjugaison peut également être utilisé pour définir une nouvelle transformation, étroitement liée à la DFT, ce est- involutive qui est, qui est son propre inverse. En particulier,  est clairement son propre inverse:
est clairement son propre inverse: 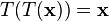 . Une transformation involutive étroitement apparenté (par un facteur de (1 + i) / √2) est
. Une transformation involutive étroitement apparenté (par un facteur de (1 + i) / √2) est  , Depuis la
, Depuis la  facteurs
facteurs  annuler l'2. Pour les entrées réelles
annuler l'2. Pour les entrées réelles 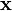 , La partie réelle de
, La partie réelle de 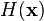 ne est autre que la transformée de Hartley discrète, qui est également involutive.
ne est autre que la transformée de Hartley discrète, qui est également involutive.
Valeurs et vecteurs propres
Les valeurs propres de la matrice DFT sont simples et bien connu, alors que les vecteurs propres sont compliquées, pas unique, et font l'objet de recherches.
Considérons la forme unitaire  défini ci-dessus pour la longueur de DFT
défini ci-dessus pour la longueur de DFT 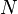 Où
Où  . Cette matrice vérifie l'équation:
. Cette matrice vérifie l'équation:
Ceci peut être vu à partir des propriétés inverses ci-dessus: en service  donne deux fois les données originales dans l'ordre inverse, afin d'exploitation
donne deux fois les données originales dans l'ordre inverse, afin d'exploitation  quatre fois redonne les données d'origine et est ainsi le matrice identité. Cela signifie que les valeurs propres
quatre fois redonne les données d'origine et est ainsi le matrice identité. Cela signifie que les valeurs propres  satisfaire une équation caractéristique:
satisfaire une équation caractéristique:
Par conséquent, les valeurs propres de  sont la quatrième racines de l'unité:
sont la quatrième racines de l'unité:  est une, -1, + i, ou - i.
est une, -1, + i, ou - i.
Depuis il ya seulement quatre valeurs propres distinctes pour ce 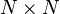 matrice, ils ont une certaine multiplicité . La multiplicité donne le nombre de vecteurs propres linéairement indépendants correspondant à chaque valeur propre. (Notez qu'il existe N vecteurs propres indépendants; une matrice unitaire ne est jamais défectueux.)
matrice, ils ont une certaine multiplicité . La multiplicité donne le nombre de vecteurs propres linéairement indépendants correspondant à chaque valeur propre. (Notez qu'il existe N vecteurs propres indépendants; une matrice unitaire ne est jamais défectueux.)
Le problème de leur multiplicité a été résolu par McClellan et des Parcs (1972), bien qu'il ait été révélé plus tard avoir été équivalent à un problème résolu par Gauss (Dickinson et Steiglitz, 1982). La multiplicité dépend de la valeur de 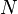 modulo 4, et est donné par le tableau suivant:
modulo 4, et est donné par le tableau suivant:
| taille N | λ = 1 | λ = -1 | λ = - i | λ + i = |
|---|---|---|---|---|
| 4 m | m + 1 | m | m | m - 1 |
| 4 m + 1 | m + 1 | m | m | m |
| 4 m 2 + | m + 1 | m + 1 | m | m |
| 4 m + 3 | m + 1 | m + 1 | m + 1 | m |
Malheureusement, pas de formule analytique simple pour les vecteurs propres est connu. En outre, les vecteurs propres ne sont pas uniques car toute combinaison linéaire des vecteurs propres pour la même valeur propre est aussi un vecteur propre pour cette valeur propre. Différents chercheurs ont proposé différents choix de vecteurs propres, sélectionné pour satisfaire des propriétés utiles comme orthogonalité et d'avoir des formes "simples" (par exemple, McClellan et des Parcs, 1972; Dickinson et Steiglitz, 1982; Grünbaum, 1982; Atakishiyev et loup, 1997;. Candan et al, 2000; Hanna et al., 2004).
Le choix des vecteurs propres de la matrice DFT a pris de l'importance ces dernières années dans le but de définir un analogue discret de la transformée de Fourier-fractionnée matrice DFT peuvent être prises pour les puissances fractionnaires par exponentiation des valeurs propres (par exemple, Rubio et Santhanam, 2005). Pour le continue à transformée de Fourier, les fonctions propres orthogonales naturels sont la Fonctions de Hermite, pour divers analogues discrètes de celles-ci ont été utilisés comme vecteurs propres de la TFD, tels que la Polynômes Kravchuk (Atakishiyev et Wolf, 1997). Le «meilleur» choix de vecteurs propres à définir une transformée de Fourier discrète fractionnée reste une question ouverte, cependant.
Le DFT réelle entrée
Si 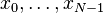 sont des nombres réels , car elles sont souvent dans des applications pratiques, la DFT obéit à la symétrie:
sont des nombres réels , car elles sont souvent dans des applications pratiques, la DFT obéit à la symétrie:
où l'étoile désigne conjugaison complexe et les indices sont interprétés modulo N.
Par conséquent, la sortie DFT pour les entrées réelles est moitié redondante, et l'on obtient l'information complète en ne regardant à peu près la moitié des sorties  . Dans ce cas, l'élément "DC"
. Dans ce cas, l'élément "DC"  est purement réel, et même pour l'élément n "Nyquist"
est purement réel, et même pour l'élément n "Nyquist" 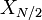 est aussi réel, donc il ya exactement N non redondants nombres réels au premier semestre + élément de Nyquist de la sortie complexe X.
est aussi réel, donc il ya exactement N non redondants nombres réels au premier semestre + élément de Nyquist de la sortie complexe X.
Utilisation La formule d'Euler, le polynôme d'interpolation trigonométrique peut alors être interprétée comme une somme de fonctions sinus et cosinus.
Généralisé / décalé DFT
Il est possible de décaler l'échantillonnage transformer dans le temps et / ou dans le domaine fréquentiel par certains changements réels a et b, respectivement. Ce est parfois connu comme un DFT généralisée (ou GDFT), aussi appelé le DFT DFT déplacé ou offset, et possède des propriétés analogues à la DFT ordinaire:
Le plus souvent, décale de  (La moitié d'un échantillon) sont utilisés. Bien que la DFT ordinaire correspond à un signal périodique à la fois dans les domaines temporel et de fréquence,
(La moitié d'un échantillon) sont utilisés. Bien que la DFT ordinaire correspond à un signal périodique à la fois dans les domaines temporel et de fréquence,  produit un signal qui est anti-périodique dans le domaine fréquentiel (
produit un signal qui est anti-périodique dans le domaine fréquentiel ( 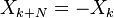 ) Et vice-versa pour
) Et vice-versa pour  . Ainsi, le cas spécifique de
. Ainsi, le cas spécifique de 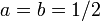 est connu comme un impair temps impair fréquence transformée de Fourier discrète (ou O 2 DFT). Cette décalé transformations sont le plus souvent utilisés pour les données symétriques, pour représenter les différentes symétries limites, et pour les données réelles symétriques qu'ils correspondent aux différentes formes de la discrète et cosinus transformations sinus.
est connu comme un impair temps impair fréquence transformée de Fourier discrète (ou O 2 DFT). Cette décalé transformations sont le plus souvent utilisés pour les données symétriques, pour représenter les différentes symétries limites, et pour les données réelles symétriques qu'ils correspondent aux différentes formes de la discrète et cosinus transformations sinus.
Un autre choix est intéressant  , Qui est appelé le DFT centrée (ou CDFT). Le DFT centrée a la propriété utile que, lorsque
, Qui est appelé le DFT centrée (ou CDFT). Le DFT centrée a la propriété utile que, lorsque 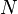 est un multiple de quatre, chacune de ses quatre valeurs propres (voir ci-dessus) ont multiplicités égales (Rubio et Santhanam, 2005).
est un multiple de quatre, chacune de ses quatre valeurs propres (voir ci-dessus) ont multiplicités égales (Rubio et Santhanam, 2005).
La transformée de Fourier discrète peut être considérée comme un cas particulier de la transformée en z, évalués sur le cercle unité dans le plan complexe; plus z transformations générales correspondent à des changements complexes a et b ci-dessus.
Multidimensionnelle DFT
Le DFT ordinaire calcule le transformer d'un ensemble de données "unidimensionnel": une séquence (ou array)  ce est une fonction d'une variable discrète
ce est une fonction d'une variable discrète 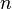 . Plus généralement, on peut définir le DFT multidimensionnelle d'un tableau multidimensionnel
. Plus généralement, on peut définir le DFT multidimensionnelle d'un tableau multidimensionnel 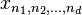 ce est une fonction de
ce est une fonction de  variables discrètes
variables discrètes 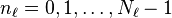 pour
pour 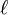 en
en 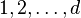 :
:
où 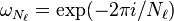 comme ci-dessus et le
comme ci-dessus et le  Les indices de production exécutés à partir
Les indices de production exécutés à partir  . Ceci est exprimé dans plus compacte notation vectorielle, où nous définissons
. Ceci est exprimé dans plus compacte notation vectorielle, où nous définissons  et
et 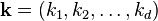 comme
comme  vecteurs de dimension des indices de 0 à
vecteurs de dimension des indices de 0 à 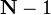 , Que nous définissons comme
, Que nous définissons comme  :
:
où la division 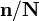 est défini comme étant
est défini comme étant 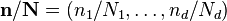 à effectuer élément par élément, et la somme représente l'ensemble des sommations imbriqués ci-dessus.
à effectuer élément par élément, et la somme représente l'ensemble des sommations imbriqués ci-dessus.
L'inverse de la transformée DFT multidimensionnelle est analogue au cas unidimensionnel, donnée par:
Le multidimensionnelle DFT a une interprétation simple. Tout comme le DFT unidimensionnelle exprime l'entrée  comme une superposition de sinusoïdes, la DFT multidimensionnel exprime l'entrée comme une superposition de ondes planes, ou sinusoïdes oscillant long de la direction
comme une superposition de sinusoïdes, la DFT multidimensionnel exprime l'entrée comme une superposition de ondes planes, ou sinusoïdes oscillant long de la direction 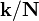 dans l'espace et ayant une amplitude
dans l'espace et ayant une amplitude  . Une telle décomposition est d'une grande importance pour tout, de traitement numérique de l'image (d = 2) pour résoudre des équations aux dérivées partielles en trois dimensions (d = 3) en brisant la solution dans des ondes planes.
. Une telle décomposition est d'une grande importance pour tout, de traitement numérique de l'image (d = 2) pour résoudre des équations aux dérivées partielles en trois dimensions (d = 3) en brisant la solution dans des ondes planes.
Calcul, la DFT multidimensionnel est simplement la composition d'une séquence de TFD à une dimension le long de chaque dimension. Par exemple, dans le cas bidimensionnel 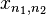 on peut d'abord calculer la
on peut d'abord calculer la  TFD indépendants des rangées (par exemple, le long de
TFD indépendants des rangées (par exemple, le long de 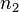 ) Pour former une nouvelle matrice
) Pour former une nouvelle matrice  , Puis calculer la
, Puis calculer la 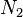 TFD indépendants
TFD indépendants  le long des colonnes (le long de
le long des colonnes (le long de  ) Pour former le résultat final
) Pour former le résultat final 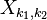 . Ou, on peut transformer les colonnes et les lignes puis-l'ordre est sans importance parce que les sommations imbriqués ci-dessus trajet .
. Ou, on peut transformer les colonnes et les lignes puis-l'ordre est sans importance parce que les sommations imbriqués ci-dessus trajet .
De ce fait, compte tenu de façon à calculer une DFT unidimensionnelle (par exemple, un algorithme FFT unidimensionnelle ordinaire), on a immédiatement un moyen pour calculer efficacement la DFT multidimensionnel. Ceci est connu comme un algorithme ligne-colonne, mais il ya aussi intrinsèquement algorithmes FFT multidimensionnels.
La véritable entrée multidimensionnelle DFT
Si les entrées 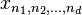 sont des nombres réels , car elles sont souvent dans des applications pratiques, les sorties DFT présentent une symétrie conjugué similaire au cas unidimensionnel ci-dessus:
sont des nombres réels , car elles sont souvent dans des applications pratiques, les sorties DFT présentent une symétrie conjugué similaire au cas unidimensionnel ci-dessus:
où l'étoile représente la conjugaison complexe et le 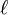 indice -ième est interprétée modulo
indice -ième est interprétée modulo  (Par
(Par  ).
).
Applications
Le DFT a vu une large utilisation dans un grand nombre de domaines; nous ne esquissons quelques exemples ci-dessous (voir aussi les références à la fin). Toutes les applications de la TFD dépendent essentiellement de la disponibilité d'un algorithme rapide pour calculer des transformées de Fourier discrète et leurs inverses, un transformée de Fourier rapide.
L'analyse spectrale
Lorsque la TFD est utilisé pour analyse spectrale, la  séquence représente généralement un ensemble fini de uniformément espacés temps-échantillons de quelque signal
séquence représente généralement un ensemble fini de uniformément espacés temps-échantillons de quelque signal 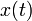 , Où t représente le temps. La conversion du temps continu aux échantillons (en temps discret) change le sous-jacent Transformée de Fourier de x (t) dans un Fourier discrète en temps de transformer (DTFT), ce qui implique généralement un type de distorsion appelé aliasing. Choix d'une fréquence d'échantillonnage approprié (voir Fréquence de Nyquist) est la clé de minimiser cette distorsion. De même, la conversion d'une séquence très long (ou infinie) à une taille implique un type de distorsion appelée fuites, qui se manifeste comme une perte de détail (résolution alias) dans le DTFT. Choix d'une longueur sous-séquence appropriée est la clé primaire de minimiser cet effet. Lorsque les données disponibles (et de temps pour le traiter) est supérieure à la quantité nécessaire pour atteindre la résolution de fréquence désirée, une technique classique consiste à effectuer plusieurs TFD, par exemple pour créer une spectrogramme. Si le résultat souhaité est un spectre de puissance et le bruit aléatoire ou est présente dans les données, la moyenne des composantes d'amplitude de la TFD multiple est un procédé utile pour réduire la variance du spectre (également appelée périodogramme dans ce contexte); deux exemples de ces techniques sont le Procédé et le Welch Méthode Bartlett.
, Où t représente le temps. La conversion du temps continu aux échantillons (en temps discret) change le sous-jacent Transformée de Fourier de x (t) dans un Fourier discrète en temps de transformer (DTFT), ce qui implique généralement un type de distorsion appelé aliasing. Choix d'une fréquence d'échantillonnage approprié (voir Fréquence de Nyquist) est la clé de minimiser cette distorsion. De même, la conversion d'une séquence très long (ou infinie) à une taille implique un type de distorsion appelée fuites, qui se manifeste comme une perte de détail (résolution alias) dans le DTFT. Choix d'une longueur sous-séquence appropriée est la clé primaire de minimiser cet effet. Lorsque les données disponibles (et de temps pour le traiter) est supérieure à la quantité nécessaire pour atteindre la résolution de fréquence désirée, une technique classique consiste à effectuer plusieurs TFD, par exemple pour créer une spectrogramme. Si le résultat souhaité est un spectre de puissance et le bruit aléatoire ou est présente dans les données, la moyenne des composantes d'amplitude de la TFD multiple est un procédé utile pour réduire la variance du spectre (également appelée périodogramme dans ce contexte); deux exemples de ces techniques sont le Procédé et le Welch Méthode Bartlett.
Une dernière source de distorsion (ou peut-être illusion) est la transformée DFT lui-même, parce que ce ne est qu'un échantillon de la DTFT discrète, qui est une fonction d'un domaine fréquentiel continu. Ce peut être atténué par l'augmentation de la résolution de la TFD. Cette procédure est illustrée dans le temps discret transformée de Fourier article.
- La procédure est parfois appelée zéro rembourrage, qui est un mode de réalisation particulier est utilisé en conjonction avec le transformée de Fourier rapide (FFT). L'inefficacité du effectuer des multiplications et des additions avec zéro-évaluée "échantillons" est plus que compensée par l'efficacité intrinsèque de la FFT.
- Comme déjà indiqué, les fuites impose une limite sur la résolution inhérente à la DTFT. Donc, il ya une limite pratique à l'avantage qui peut être obtenu à partir d'un DFT fine.
La compression de données
Le domaine du traitement de signal numérique se appuie fortement sur les opérations dans le domaine de fréquence (ce est à dire sur la transformée de Fourier). Par exemple, plusieurs l'image avec perte et les méthodes de compression audio emploient transformée de Fourier discrète: le signal est découpé en courts segments, chacun se transforme, puis les coefficients de Fourier de hautes fréquences, qui sont supposés être imperceptible, sont rejetés. Le décompresseur calcule la transformée inverse sur la base de ce nombre réduit de coefficients de Fourier. (Applications de compression utilisent souvent une forme spécialisée de la TFD, le transformée en cosinus discrète ou parfois le transformer cosinus discrète modifiée).
Équations aux dérivées partielles
Transformées de Fourier discrètes sont souvent utilisés pour résoudre des équations aux dérivées partielles , où de nouveau la DFT est utilisée comme une approximation pour le série de Fourier (qui est récupéré dans la limite de N infinie). L'avantage de cette approche est qu'elle élargit le signal dans exponentielles complexes e inx, qui sont propres de la différenciation: d dx e inx / = e dans inx. Ainsi, dans la représentation de Fourier, la différenciation est simple-nous multiplions simplement en en. Une équation différentielle linéaire à coefficients constants est transformée en une équation algébrique facilement résoluble. On utilise alors la TFD inverse pour transformer le résultat dans la représentation spatiale ordinaire. Une telle approche est appelée méthode spectrale.
Multiplication polynomiale
Supposons que nous souhaitons pour calculer le produit polynôme c (x) = a (x) · b (x). L'expression du produit ordinaire pour les coefficients de c implique un linéaire (acyclique) convolution, où les indices ne ont pas "se enrouler autour." Ceci peut être réécrite sous la forme d'une convolution cyclique en prenant les vecteurs de coefficients de a (x) et b (x) avec terme constant, puis l'ajout de zéros de sorte que le coefficient résultant des vecteurs a et b ont la dimension d> deg (a (x) ) + deg (b (x)). Ensuite,
Où c est le vecteur des coefficients C (x), et l'opérateur de convolution  est défini de sorte
est défini de sorte
Mais convolution devient multiplication sous la DFT:
Voici le produit vectoriel est prise élément par élément. Ainsi, les coefficients du produit polynôme C (X) ne sont que les termes 0, ..., deg (a (x)) + deg (b (x)) du vecteur de coefficient
Avec un Transformée de Fourier rapide, l'algorithme résultant prend O (n log n) opérations arithmétiques. En raison de sa simplicité et de rapidité, le Cooley-Tukey algorithme FFT, qui est limitée à tailles composites, est souvent choisi pour l'opération de transformation. Dans ce cas, d doit être choisi comme le plus petit entier plus grand que la somme des degrés de polynômes entrée qui est factorisable en petits facteurs premiers (par exemple de 2, 3 et 5, en fonction de l'application de la FFT).
Multiplication des grands entiers
Le plus rapide connue algorithmes pour la multiplication de très grands nombres entiers utilisent la méthode de multiplication polynôme indiqué ci-dessus. Les entiers peuvent être traitées comme la valeur d'un polynôme évalué spécifiquement à la base du numéro, avec les coefficients du polynôme correspondant à des chiffres dans ladite base. Après multiplication polynomiale, une étape de propagation de relativement faible complexité complète la multiplication.
Certains de transformée de Fourier discrète paires
 |  | Note |
|---|---|---|
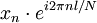 |  | Maj théorème |
 | 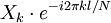 | |
 |  | Immobilier DFT |
 | 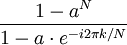 | |
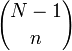 |  |
Dérivation en série de Fourier
La DFT peut être calculée comme une troncature de la série de Fourier d'une suite périodique de impulsions.
DFT sur les champs autres que les nombres complexes
Un grand nombre des propriétés de la transformée DFT ne dépendent que du fait que 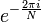 est un racine primitive de l'unité, parfois notée
est un racine primitive de l'unité, parfois notée  ou
ou  (De sorte que
(De sorte que  ). Ces propriétés comprennent l'exhaustivité, l'orthogonalité, Plancherel / Parseval, la périodicité, décalage, convolution, et les propriétés de unitarité ci-dessus, ainsi que de nombreux algorithmes FFT. Pour cette raison, la transformée de Fourier discrète peut être défini à l'aide de racines de l'unité en d'autres domaines que les nombres complexes; Pour plus d'informations, voir transformée de Fourier discrète (général).
). Ces propriétés comprennent l'exhaustivité, l'orthogonalité, Plancherel / Parseval, la périodicité, décalage, convolution, et les propriétés de unitarité ci-dessus, ainsi que de nombreux algorithmes FFT. Pour cette raison, la transformée de Fourier discrète peut être défini à l'aide de racines de l'unité en d'autres domaines que les nombres complexes; Pour plus d'informations, voir transformée de Fourier discrète (général).