Mécanique statistique
Renseignements généraux
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Voir http://www.soschildren.org/sponsor-a-child pour connaître le parrainage d'enfants.
| Mécanique statistique |
|---|
 |
|
Statistiques de particules
|
Ensembles
|
Modèles
|
Potentiels
|
La mécanique statistique est l'application de la théorie des probabilités , qui comprend mathématiques des outils pour faire face à de grandes populations, dans le domaine de mécanique, qui est concerné par le mouvement des particules ou des objets lorsqu'il est soumis à une force. Mécanique statistique, parfois appelés physique statistique, peut être considéré comme un sous-domaine de la physique et de la chimie .
Il fournit un cadre pour relier les propriétés microscopiques des atomes et des molécules individuelles aux propriétés macroscopiques ou en vrac de matières qui peuvent être observés dans la vie quotidienne, ce qui explique donc la thermodynamique comme un résultat naturel des statistiques et de la mécanique (classique et quantique) à l'échelle microscopique . En particulier, il peut être utilisé pour calculer les propriétés thermodynamiques des matériaux en vrac à partir des données spectroscopiques des molécules individuelles.
Cette capacité à faire des prédictions basées sur les propriétés macroscopiques microscopiques est le principal avantage de la mécanique statistique plus de la thermodynamique . Les deux théories sont régies par la seconde loi de la thermodynamique par l'intermédiaire de l'entropie . Cependant, l'entropie en thermodynamique ne peut être connu de manière empirique, alors que dans la mécanique statistique, ce est une fonction de la distribution du système sur ses micro-Unis.
Postulat fondamental
Le postulat fondamental en mécanique statistique (également connu sous le nom une probabilité égale postulat priori) est la suivante:
- Étant donné un système isolé à l'équilibre, il est constaté avec la même probabilité dans chacun de ses accessible microétats.
Ce postulat est une hypothèse fondamentale en mécanique statistique - il est dit que un système en équilibre n'a pas de préférence pour l'un de ses micro-disponibles. Compte tenu de micro-Ω à une énergie particulière, la probabilité de trouver le système dans un micro-état particulier est p = 1 / Ω.
Ce postulat est nécessaire car elle permet de conclure que pour un système à l'équilibre, l'état thermodynamique (macroscopique) qui pourrait résulter de la plus grande nombre de micro est également le macroétat plus probable du système.
Le postulat est justifiée en partie, pour les systèmes classiques, par Théorème de Liouville (hamiltonien), ce qui montre que si la répartition des points grâce système accessible espace des phases est uniforme à un certain moment, il reste donc parfois plus tard.
Similaire justification pour un système discret est fourni par le mécanisme de bilan détaillé.
Cela permet la définition de la fonction de l'information (dans le contexte de théorie de l'information):
Lorsque tous rhos sont égaux, I est minime, ce qui reflète le fait que nous avons un minimum d'informations sur le système. Lorsque notre information est maximale, ce est à dire une rho est égal à un et le reste à zéro (on sait dans quel état le système est en), la fonction est maximale.
Cette fonction "information" est la même que la fonction d'entropie en thermodynamique réduite.
Ensemble microcanonique
En ensemble microcanonique N, V et E sont fixés. Depuis la seconde loi de la thermodynamique se applique à systèmes isolés, le premier cas d'une enquête correspondra à ce cas. L'ensemble microcanonique décrit une système isolé.
L' entropie d'un tel système ne peut augmenter, de sorte que le maximum de son entropie correspond à une état d'équilibre du système.
Parce qu'un système isolé conserve une énergie constante, le total de l'énergie du système ne fluctue pas. Ainsi, le système ne peut accéder qu'à ceux de ses micro-états qui correspondent à une valeur donnée E de l'énergie. Le l'énergie interne du système est alors rigoureusement égale à son énergie .
Appelons  le nombre de micro-états correspondant à cette valeur de l'énergie du système. L'état macroscopique maximale entropie du système est celui dans lequel tous les micro-états sont également susceptibles de se produire, avec une probabilité
le nombre de micro-états correspondant à cette valeur de l'énergie du système. L'état macroscopique maximale entropie du système est celui dans lequel tous les micro-états sont également susceptibles de se produire, avec une probabilité 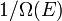 , Durant les fluctuations du système.
, Durant les fluctuations du système.
- où
 est le système d'entropie ,
est le système d'entropie , 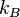 est La constante de Boltzmann
est La constante de Boltzmann
Ensemble canonique
En ensemble canonique N, V et T sont fixés. Appel du concept de l'ensemble canonique, il est possible de déduire la probabilité  que dans un système macroscopique équilibre thermique avec son environnement, sera dans un état microscopique donnée à l'énergie
que dans un système macroscopique équilibre thermique avec son environnement, sera dans un état microscopique donnée à l'énergie  selon le Distribution de Boltzmann:
selon le Distribution de Boltzmann:
- où
 ,
,
La température 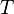 provient du fait que le système est en équilibre thermique avec son environnement. Les probabilités des différents micro-doivent ajouter à une, et de la facteur de normalisation dans le dénominateur est le canonique fonction de partition:
provient du fait que le système est en équilibre thermique avec son environnement. Les probabilités des différents micro-doivent ajouter à une, et de la facteur de normalisation dans le dénominateur est le canonique fonction de partition:
où  est l'énergie de la
est l'énergie de la  e microscopique du système. La fonction de partition est une mesure du nombre d'états accessibles au système à une température donnée. L'article ensemble canonique contient une dérivation du facteur de Boltzmann et la forme de la fonction de partition à partir des premiers principes.
e microscopique du système. La fonction de partition est une mesure du nombre d'états accessibles au système à une température donnée. L'article ensemble canonique contient une dérivation du facteur de Boltzmann et la forme de la fonction de partition à partir des premiers principes.
Pour résumer, la probabilité de trouver un système à la température 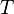 dans un état particulier de l'énergie
dans un état particulier de l'énergie  est
est
Connexion thermodynamique
La fonction de partition peut être utilisé pour trouver la valeur (moyenne) prévue de ne importe quelle propriété microscopique du système, qui peut ensuite être liée à des variables macroscopiques. Par exemple, la valeur attendue de l'énergie microscopique  est interprété comme la définition microscopique de l'énergie interne variable thermodynamique
est interprété comme la définition microscopique de l'énergie interne variable thermodynamique 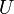 ., Et peut être obtenu en prenant la dérivée de la fonction de partition par rapport à la température. En Effet,
., Et peut être obtenu en prenant la dérivée de la fonction de partition par rapport à la température. En Effet,
implique, en collaboration avec l'interprétation de  comme
comme 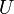 , La définition suivante de microscopiques énergie interne:
, La définition suivante de microscopiques énergie interne:
L'entropie peut être calculé par (voir Entropie de Shannon)
ce qui implique que
est le l'énergie libre du système ou en d'autres termes,
Ayant expressions microscopiques pour les potentiels thermodynamiques de base 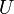 ( énergie interne),
( énergie interne),  ( entropie ) et
( entropie ) et 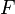 ( énergie libre) est suffisante pour obtenir des expressions pour d'autres grandeurs thermodynamiques. La stratégie de base est la suivante. Il peut y avoir une quantité intensive ou extensive qui entre explicitement dans l'expression de l'énergie microscopique
( énergie libre) est suffisante pour obtenir des expressions pour d'autres grandeurs thermodynamiques. La stratégie de base est la suivante. Il peut y avoir une quantité intensive ou extensive qui entre explicitement dans l'expression de l'énergie microscopique  , Pour le champ magnétique de l'instance (intensive) ou le volume (vaste). Ensuite, les variables thermodynamiques conjuguées sont des dérivés de l'énergie interne. L'aimantation macroscopique (large) est la dérivée de
, Pour le champ magnétique de l'instance (intensive) ou le volume (vaste). Ensuite, les variables thermodynamiques conjuguées sont des dérivés de l'énergie interne. L'aimantation macroscopique (large) est la dérivée de 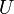 en ce qui concerne le (intensive) de champ magnétique, et la pression (intensité) est la dérivée de
en ce qui concerne le (intensive) de champ magnétique, et la pression (intensité) est la dérivée de 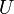 par rapport au volume (vaste).
par rapport au volume (vaste).
Le traitement de cette section ne assume aucune échange de matière (masse-à-dire fixe et nombre de particules fixes). Cependant, le volume du système est variable ce qui signifie que la densité est également variable.
Cette probabilité peut être utilisé pour trouver la valeur moyenne, ce qui correspond à la valeur macroscopique, de tous biens,  , Cela dépend de l'état énergétique du système en utilisant la formule:
, Cela dépend de l'état énergétique du système en utilisant la formule:
où 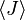 est la valeur moyenne des biens
est la valeur moyenne des biens 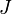 . Cette équation peut être appliquée à l'énergie interne,
. Cette équation peut être appliquée à l'énergie interne, 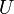 :
:
Par la suite, ces équations peuvent être combinées avec des relations thermodynamiques connues entre 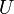 et
et  pour arriver à une expression de la pression en termes de température seulement, le volume et la fonction de partition. Des relations similaires en termes de la fonction de partition peuvent être dérivées d'autres propriétés thermodynamiques comme indiqué dans le tableau ci-dessous; vous pouvez aussi consulter les explications détaillées dans configuration intégrale.
pour arriver à une expression de la pression en termes de température seulement, le volume et la fonction de partition. Des relations similaires en termes de la fonction de partition peuvent être dérivées d'autres propriétés thermodynamiques comme indiqué dans le tableau ci-dessous; vous pouvez aussi consulter les explications détaillées dans configuration intégrale.
| Helmholtz énergie libre: | 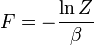 |
|---|---|
| L'énergie interne: |  |
| Pression: |  |
| Entropie : |  |
| Gibbs l'énergie libre : |  |
| Enthalpie : | 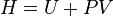 |
| Volume constant la capacité de la chaleur: | 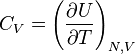 |
| Constant capacité calorifique de pression: |  |
| Potentiel chimique: |  |
Pour clarifier, ce ne est pas un grand ensemble canonique.
Il est souvent utile de considérer l'énergie d'une molécule donnée à distribuer parmi un certain nombre de modes. Par exemple, l'énergie de translation se réfère à cette partie de l'énergie associée au mouvement du centre de masse de la molécule. Configurationnel énergie se réfère à cette partie de l'énergie associée aux différentes forces d'attraction et de répulsion entre les molécules dans un système. Les autres modes sont tous considérés comme interne à chaque molécule. Ils comprennent les modes de rotation, de vibration, électroniques et nucléaires. Si l'on suppose que chaque mode est indépendant (une hypothèse discutable) l'énergie totale peut être exprimée comme la somme de chacun des composants:
Où les indices  ,
,  ,
,  ,
,  ,
,  Et
Et  correspondre à la traduction, configurationnelle, nucléaire, modes électroniques, rotation et de vibration, respectivement. La relation dans cette équation peut être substitué dans la première équation pour donner:
correspondre à la traduction, configurationnelle, nucléaire, modes électroniques, rotation et de vibration, respectivement. La relation dans cette équation peut être substitué dans la première équation pour donner:
Si nous pouvons supposer tous ces modes sont complètement découplé et non corrélées, de sorte que tous ces facteurs sont en un sens de probabilité complètement indépendant, puis
Ainsi, une fonction de partition peut être définie pour chaque mode. Les expressions simples ont été obtenus concernant chacun des différents modes de diverses propriétés moléculaires mesurables, tels que les fréquences de rotation ou de vibration caractéristiques.
Les expressions pour les différentes fonctions de partition moléculaires sont indiquées dans le tableau suivant.
| Nucléaire | 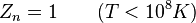 |
|---|---|
| Électronique | 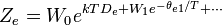 |
| Vibratoire |  |
| Rotation (linéaire) |  |
| De rotation (non linéaire) | 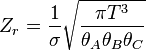 |
| Translationnelle | 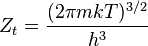 |
| Configurationnelle (gaz idéal) | 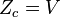 |
Ces équations peuvent être combinés avec ceux de la première table pour déterminer la contribution d'un mode d'énergie en particulier à une propriété thermodynamique. Par exemple, la «pression de rotation" peut être déterminée de cette manière. La pression totale pourrait être trouvé en additionnant les contributions de pression de tous les différents modes, à savoir:
Ensemble grand-canonique
En grande canonique ensemble V, T et le potentiel chimique sont fixés. Si le système à l'étude est un système ouvert, (matière peut être échangé), mais le nombre de particules ne est pas conservée, nous aurions à introduire potentiels chimiques, μ j, j = 1, ..., n et le remplacer canonique fonction de partition avec le grande fonction de partition canonique:
où N ij est le nombre de particules de j-ième espèces dans la i ème configuration. Parfois, nous avons aussi d'autres variables à ajouter au fonction de partition, l'une correspondant à chaque quantité conservée. La plupart d'entre eux, cependant, peut être interprété comme toute sécurité potentiels chimiques. Dans la plupart des systèmes de la matière condensée, les choses sont non relativiste et la masse est conservée. Cependant, la plupart des systèmes d'intérêt de la matière condensée conservent également le nombre de particules d'environ (métastable) et la masse (non relativiste) ne est autre que la somme du nombre de chaque type de temps de particules sa masse. La masse est inversement proportionnelle à la densité, qui est la variable conjuguée à la pression. Pour le reste de cet article, nous allons ignorer cette complication et prétendre potentiels chimiques ne comptent pas. Voir grand ensemble canonique.
Disons retravailler tout en utilisant un ensemble grand-canonique cette fois. Le volume est laissé fixe et ne figure pas dans du tout dans ce traitement. Comme auparavant, j est l'indice pour les particules de l'espèce j et i est l'indice de microétat i:
| Grand potentiel: |  |
| L'énergie interne: | 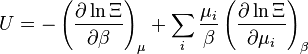 |
| nombre de particules: |  |
| Entropie : |  |
| Helmholtz énergie libre: |  |
Equivalence entre descriptions au limite thermodynamique
Toutes les descriptions ci-dessus diffèrent dans la manière dont ils permettent au système donné à fluctuer entre ses configurations.
Dans le micro-canonique ensemble, les échanges de système pas d'énergie avec le monde extérieur, et ne est donc pas soumis aux fluctuations de l'énergie, alors que dans l'ensemble canonique, le système est libre d'échanger de l'énergie avec l'extérieur sous forme de chaleur .
Dans le limite thermodynamique, qui est la limite de grands systèmes, les variations deviennent négligeables, de sorte que toutes ces descriptions convergent vers la même description. En d'autres termes, le comportement macroscopique d'un système ne dépend pas de l'ensemble particulier utilisé pour sa description.
Compte tenu de ces considérations, le meilleur ensemble de choisir pour le calcul des propriétés d'un système macroscopique est cet ensemble qui permet le résultat le plus facilement être dérivé.
Marcheurs aléatoires
L'étude de la longue chaîne polymères a été une source de problèmes dans les domaines de la mécanique statistique depuis environ les années 1950. Une des raisons, cependant, que les scientifiques étaient intéressés dans leur étude est que les équations régissant le comportement d'une chaîne de polymère étaient indépendants de la chimie de la chaîne. Qui plus est, l'équation régissant avère être un aléatoire (diffusion) marche dans l'espace. En effet, l'équation de Schrödinger est elle-même une équation de diffusion en temps imaginaire, 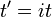 .
.
Marches aléatoires dans le temps
Le premier exemple d'une marche aléatoire est une dans l'espace, grâce à quoi une particule subit un mouvement aléatoire en raison des forces externes dans son milieu environnant. Un exemple typique serait un grain de pollen dans un bécher d'eau. Si l'on pouvait en quelque sorte "teindre" le chemin du grain de pollen a pris, le chemin observé est défini comme une marche aléatoire.
Considérons un problème de jouet, d'un train se déplaçant le long d'une piste 1D dans la direction x. Supposons que le train se déplace soit une distance de + ou - une distance fixe b, selon que une pièce de monnaie atterrit pile ou face quand renversé. Permet de commencer par examiner les statistiques des étapes du train jouet prend (où 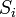 est l'étape ième prises):
est l'étape ième prises):
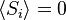 ; en raison de probabilités a priori égales
; en raison de probabilités a priori égales 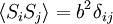
La seconde quantité est connue comme la la fonction de corrélation. Le delta est la Kronecker qui nous dit que si les indices i et j sont différents, alors le résultat est 0, mais si i = j alors la Kronecker est une, de sorte que le fonction de corrélation renvoie une valeur de  . Ce est logique, car si i = j alors nous envisageons la même étape. Plutôt trivialement alors il peut être établi que la moyenne de déplacement du train sur l'axe des x est égal à 0;
. Ce est logique, car si i = j alors nous envisageons la même étape. Plutôt trivialement alors il peut être établi que la moyenne de déplacement du train sur l'axe des x est égal à 0;
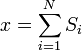


Comme indiqué  est égal à 0, de sorte que la somme de 0 est toujours 0. Il peut également être représenté, en utilisant la même méthode illustrée ci-dessus, pour calculer la valeur quadratique moyenne de problème. Le résultat de ce calcul est donnée ci-dessous
est égal à 0, de sorte que la somme de 0 est toujours 0. Il peut également être représenté, en utilisant la même méthode illustrée ci-dessus, pour calculer la valeur quadratique moyenne de problème. Le résultat de ce calcul est donnée ci-dessous
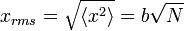
Du équation de diffusion, il peut être établi que la distance A se déplace de diffusion de particules dans un milieu est proportionnelle à la racine du moment où le système a été diffuse pour, lorsque la constante de proportionnalité est la racine de la constante de diffusion. La relation ci-dessus, bien que d'apparence différente révèle la physique similaire, où N est tout simplement le nombre de pas déménagé (est vaguement connecté avec le temps) et b est la longueur de l'étape caractéristique. En conséquence, nous pouvons considérer la diffusion comme un processus de marche aléatoire.
Marches aléatoires dans l'espace
Marches aléatoires dans l'espace peut être considéré comme des instantanés de la voie empruntée par un marcheur aléatoire dans le temps. Un tel exemple est la configuration spatiale des polymères à longue chaîne.
Il existe deux types de marche aléatoire dans l'espace: autoévitante marches aléatoires, où les liens de l'interaction de la chaîne polymère et ne se chevauchent pas dans l'espace, et les marches aléatoires purs, où les maillons de la chaîne de polymère sont sans interaction et les liens sont libres de se allonger sur un de l'autre. Le premier type est le plus applicable à des systèmes physiques, mais leurs solutions sont plus difficiles à obtenir au partir des premiers principes.
En prenant en compte, d'une chaîne articulée librement sans interaction polymère, le vecteur de bout en bout est  où
où 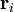 est le vecteur position de la liaison i -ième de la chaîne. En raison de la théorème central limite, si N >> 1 alors la nous nous attendons à une distribution gaussienne pour le vecteur de bout en bout. Nous pouvons aussi faire des déclarations de la statistique des liens eux-mêmes;
est le vecteur position de la liaison i -ième de la chaîne. En raison de la théorème central limite, si N >> 1 alors la nous nous attendons à une distribution gaussienne pour le vecteur de bout en bout. Nous pouvons aussi faire des déclarations de la statistique des liens eux-mêmes; 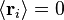 ; par l'isotropie de l'espace
; par l'isotropie de l'espace 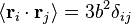 ; tous les maillons de la chaîne ne sont pas corrélés avec l'autre
; tous les maillons de la chaîne ne sont pas corrélés avec l'autre
En utilisant les statistiques des liens individuels, il est facile de montrer que  et
et 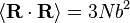 . Remarquez ce dernier résultat est le même que celui trouvé pour les marches aléatoires dans le temps.
. Remarquez ce dernier résultat est le même que celui trouvé pour les marches aléatoires dans le temps.
En supposant, comme indiqué, que cette distribution des vecteurs de bout-en-bout pour un très grand nombre de chaînes de polymère identiques est gaussienne, la distribution de probabilité a la forme suivante

Quel usage est-ce à nous? Rappelons que, selon le principe de tout aussi susceptibles probabilités a priori, le nombre de micro, Ω, à une certaine valeur physique est directement proportionnelle à la distribution de probabilité à cette valeur physique, à savoir;

où c est une constante de proportionnalité arbitraire. Compte tenu de notre fonction de distribution, il existe un maximum correspondant à 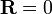 . Physiquement, cela revient à y étant plus microscopiques qui ont un vecteur de 0 que ne importe quel autre état microscopique de bout en bout. Maintenant en considérant
. Physiquement, cela revient à y étant plus microscopiques qui ont un vecteur de 0 que ne importe quel autre état microscopique de bout en bout. Maintenant en considérant 
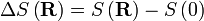
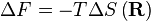
où F est la Énergie libre il est trivial de montrer que 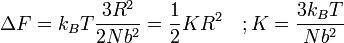
Un ressort Hookian!
Ce résultat est connu comme le Printemps Entropic Résultat et revient à dire que lors de l'étirement d'une chaîne polymère que vous faites un travail sur le système pour le faire glisser en dehors de son (préféré) état d'équilibre. Un exemple de ceci est une bande élastique commun, composé de longues chaînes de polymères (caoutchouc). En étirant l'élastique que vous faites un travail sur le système et le groupe se comporte comme un ressort classique. Ce qui est particulièrement surprenant de ce résultat cependant, est que le travail effectué à l'étirement de la chaîne de polymère peut être entièrement liée à la variation de l'entropie du système à la suite de l'étirage.






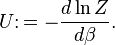


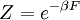

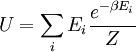
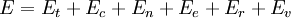

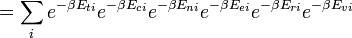


![\ Xi (V, T, \ mu) = \ sum_i \ exp \ left (\ beta \ left [\ sum_ {j = 1} ^ n \ mu_j N_ {ij} -E_i \ right] \ right)](../../images/633/63360.png)