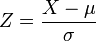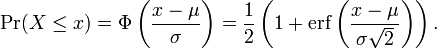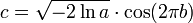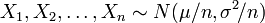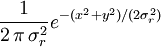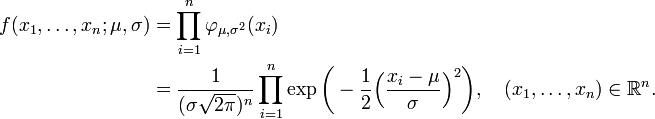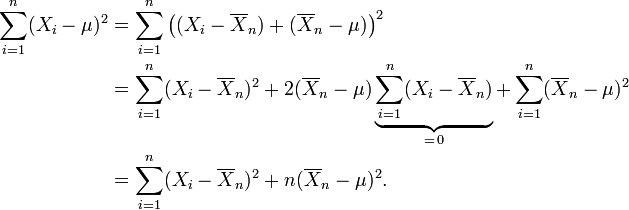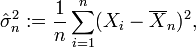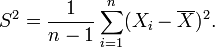Distribution normale
Contexte des écoles Wikipédia
Enfants SOS offrent un chargement complet de la sélection pour les écoles pour une utilisation sur les intranets des écoles. Cliquez ici pour plus d'informations sur les enfants SOS.
Densité de probabilité  La ligne verte est la distribution normale standard | |
Fonction de distribution cumulative  Couleurs correspondent à l'image ci-dessus | |
| Paramètres |  emplacement ( réel ) emplacement ( réel )  quadrillé échelle (réel) quadrillé échelle (réel) |
|---|---|
| Soutien | 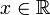 |
 | |
| CDF |  |
| Signifier |  |
| Médiane |  |
| Mode |  |
| Variance |  |
| Asymétrie | 0 |
| Ex. aplatissement | 0 |
| Entropy | 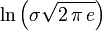 |
| MGF |  |
| FC |  |
La distribution normale, aussi appelée la distribution gaussienne, est une importante famille de distributions de probabilités continues , applicable dans de nombreux domaines. Chaque membre de la famille peut être définie par deux paramètres, l'emplacement et d'échelle: la moyenne («moyenne», μ) et la variance ( écart-type carré) σ 2, respectivement. La distribution normale est la distribution normale avec une moyenne de zéro et un écart d'une (les courbes vertes dans les parcelles vers la droite). Carl Friedrich Gauss est devenu associé à cet ensemble de distributions quand il a analysé les données astronomiques de les utiliser, et défini l'équation de la fonction de densité de probabilité. On l'appelle souvent la courbe en cloche, car le diagramme de son densité de probabilité ressemble à un cloche.
L'importance de la distribution normale en tant que modèle de phénomènes quantitatives dans le naturel et sciences du comportement est dû à la théorème central limite. Beaucoup psychologiques et mesures physiques (phénomènes comme bruit) peut être bien approchée par la distribution normale. Bien que les mécanismes qui sous-tendent ces phénomènes sont souvent inconnus, l'utilisation du modèle normal peut être justifié en supposant que théoriquement, de nombreux petits effets indépendants sont additivement contribuent à chaque observation.
La distribution normale se pose également dans de nombreux domaines de statistiques . Par exemple, le distribution d'échantillonnage de la moyenne échantillon est approximativement normale, même si la distribution de la population à partir de laquelle l'échantillon est prélevé ne est pas normal. En outre, la distribution normale maximise entropie de l'information entre toutes les distributions à moyenne et la variance connue, ce qui rend le choix naturel de distribution sous-jacente des données résumées en termes de moyenne de l'échantillon et la variance. La distribution normale est la famille la plus largement utilisée dans les statistiques des distributions et de nombreux tests statistiques sont fondées sur l'hypothèse de normalité. Dans la théorie des probabilités , distributions normales apparaissent comme limiter les distributions de plusieurs continues et discrètes familles de distributions.
Histoire
La distribution normale a été introduite par Abraham de Moivre dans un article en 1733, qui a été reproduit dans la deuxième édition de son La théorie des probabilités, 1738 dans le contexte de rapprochement de certaines distributions binomiale pour n grand. Son résultat a été prolongée par Laplace dans son livre Théorie analytique des probabilités (1812), et se appelle désormais la théorème de Moivre-Laplace.
Laplace utilise la distribution normale dans le analyse des erreurs d'expériences. L'importance méthode des moindres carrés a été introduit par Legendre en 1805. Gauss , qui prétendait avoir utilisé la méthode depuis 1794, a justifié rigoureusement en 1809 en supposant une distribution normale des erreurs.
Le nom de «courbe en cloche» remonte à Jouffret qui d'abord utilisé le terme «surface de cloche» en 1872 pour une bivariée normale avec des composants indépendants. Le nom de «distribution normale» a été inventé indépendamment par Charles S. Peirce, Francis Galton et Wilhelm Lexis vers 1875. Malgré cette terminologie, d'autres distributions de probabilité peut être plus approprié dans certains contextes; voir la discussion de survenance , ci-dessous.
Caractérisation
Il existe diverses façons à caractériser une distribution de probabilité . Le visuel est la plus fonction de densité de probabilité (PDF). Manières équivalentes sont les fonction de distribution cumulative, la moments, le cumulants, le fonction caractéristique, le Fonction génératrice des moments, le cumulant- fonction génératrice, et Le théorème de Maxwell. Voir distribution de probabilité pour une discussion.
Pour indiquer qu'une valeur réelle variable aléatoire X est normalement distribué avec une moyenne μ et de variance σ ² ≥ 0, nous écrivons
Même se il est certainement utile pour certains théorèmes limites (par exemple, normalité asymptotique des estimateurs) et de la théorie de la Processus gaussiens à considérer la distribution de probabilité concentrée à μ (voir Mesure de Dirac) comme une distribution normale de moyenne μ et de variance σ ² = 0, ce cas dégénéré est souvent exclue des considérations parce que personne ne la densité par rapport à la Mesure de Lebesgue existe.
La distribution normale peut également être paramétré en utilisant un précision paramètre τ, définie comme l'inverse de σ ². Ce paramétrage a un avantage dans les applications numériques où σ ² est très proche de zéro et est plus commode de travailler avec l'analyse que τ est un paramètre physique de la distribution normale.
Densité de probabilité

Le continu fonction de densité de probabilité de la distribution normale est le Gaussienne
où σ> 0 est l' écart-type , le paramètre μ réel est le valeur attendue, et
est la fonction de densité de la distribution normale "standard", ce est à dire, la distribution normale avec μ = 0 et σ = 1. Le intégrante de  au dessus de ligne réelle est égale à un, comme indiqué dans la Article intégrante gaussienne.
au dessus de ligne réelle est égale à un, comme indiqué dans la Article intégrante gaussienne.
Comme une fonction gaussienne avec le dénominateur de l'exposant égale à 2, la fonction de densité normale standard  est un fonction propre de la Transformée de Fourier.
est un fonction propre de la Transformée de Fourier.
La fonction de densité de probabilité présente des propriétés remarquables, notamment:
- symétrie par rapport à ses moyens μ
- la Mode et de la médiane à la fois égale à la moyenne μ
- la points de la courbe d'inflexion se produisent un écart-type loin de la moyenne, ce est à dire au μ - σ et μ + σ.
Fonction de distribution cumulative

Le fonction de distribution cumulative (CDF de) d'une distribution de probabilité , évaluée à un certain nombre (minuscules) x, est la probabilité de l'événement ayant une variable aléatoire (capital) X avec cette répartition est inférieur ou égal à x. La fonction de distribution cumulative de la distribution normale est exprimée en termes de la fonction de densité de la manière suivante:
où la fonction de répartition normale standard, Φ, est juste la cdf générale évaluée avec μ = 0 et σ = 1:
Le cdf normale standard peut être exprimée en termes de fonction spéciale appelée fonction d'erreur, en tant que
et la fonction de répartition lui-même peut donc être exprimée comme
Le complément de la fonction de répartition normale standard, 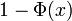 , Est souvent désigné
, Est souvent désigné  , Et est parfois désigné simplement comme la Q-fonction, en particulier dans les textes d'ingénierie. Cela représente la probabilité queue de la distribution gaussienne. D'autres définitions de la fonction de Q, qui sont toutes des transformations simples
, Et est parfois désigné simplement comme la Q-fonction, en particulier dans les textes d'ingénierie. Cela représente la probabilité queue de la distribution gaussienne. D'autres définitions de la fonction de Q, qui sont toutes des transformations simples  , Sont également utilisés parfois.
, Sont également utilisés parfois.
L'inverse fonction standard de distribution cumulative normale, ou fonction quantile, peut être exprimée en termes de la fonction d'erreur inverse:
et la fonction cumulative inverse de distribution peut donc être exprimée comme
Cette fonction quantile est parfois appelé le fonction probit. Il n'y a pas élémentaire primitive de la fonction de probit. Ce ne est pas de dire simplement que rien ne est connu, mais plutôt que la non-existence d'une telle primitive élémentaire a été prouvé. Plusieurs méthodes précises existent pour l'approximation de la fonction quantile pour la distribution normale - voir fonction quantile pour une discussion et références.
Les valeurs Φ (x) peuvent être estimés de façon très précise par une variété de méthodes, telles que l'intégration numérique , la série de Taylor , série asymptotique et fractions continues.
Limites strictes inférieures et supérieures pour la cdf
Pour les grandes x la cdf normale standard 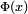 est proche de 1 et
est proche de 1 et 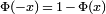 est proche de 0. Les limites élémentaires
est proche de 0. Les limites élémentaires
en termes de la densité  sont utiles.
sont utiles.
En utilisant le substitution v = u ² / 2, la limite supérieure est calculée comme suit:
De même, en utilisant  et le règle de quotient,
et le règle de quotient,
La résolution de  fournit la borne inférieure.
fournit la borne inférieure.
Fonctions génératrices
Moment fonction de production
Le fonction génératrice des moments est définie comme la valeur attendue de exp (TX). Pour une distribution normale, la fonction génératrice des moments est
comme on peut le voir par complétant le carré de l'exposant.
Fonction génératrice des cumulants
Le cumulant fonction génératrice est le logarithme de la fonction génératrice des moments: g (t) = μ t + s² t ² / 2. Puisque ce est un polynôme quadratique en t, seuls les deux premiers cumulants sont non nulles.
Fonction caractéristique
Le fonction caractéristique est définie comme la valeur attendue de  Où
Où  est l' unité imaginaire . Ainsi, la fonction caractéristique est obtenue en remplaçant
est l' unité imaginaire . Ainsi, la fonction caractéristique est obtenue en remplaçant  avec
avec  dans la fonction génératrice des moments.
dans la fonction génératrice des moments.
Pour une distribution normale, la fonction caractéristique est
Propriétés
Certaines propriétés de la distribution normale:
- Si
 et
et  et
et  sont des nombres réels , puis
sont des nombres réels , puis 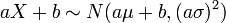 (Voir valeur attendue et la variance ).
(Voir valeur attendue et la variance ). - Si
 et
et 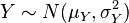 sont normales indépendantes variables aléatoires , puis:
sont normales indépendantes variables aléatoires , puis: - Leur somme est normalement distribué avec
 ( la preuve). Fait intéressant, l'inverse est vrai: si deux variables aléatoires indépendantes ont une somme normalement distribué, alors ils doivent être normales eux-mêmes - ce est connu comme Le théorème de Cramer.
( la preuve). Fait intéressant, l'inverse est vrai: si deux variables aléatoires indépendantes ont une somme normalement distribué, alors ils doivent être normales eux-mêmes - ce est connu comme Le théorème de Cramer. - Leur différence est normalement distribué avec
 .
. - Si les variances de X et Y sont égaux, alors U et V sont indépendantes les unes des autres.
- Le Kullback-Leibler,

- Leur somme est normalement distribué avec
- Si
 et
et  sont des variables aléatoires normales indépendantes, alors:
sont des variables aléatoires normales indépendantes, alors: - Leur produit
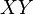 suit une distribution de densité
suit une distribution de densité 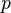 donné par
donné par  où
où 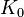 est une fonction de Bessel modifiée de deuxième espèce .
est une fonction de Bessel modifiée de deuxième espèce .
- Leur rapport suit une Distribution de Cauchy avec
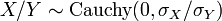 . Ainsi, la distribution de Cauchy est un type spécial de Répartition de rapport.
. Ainsi, la distribution de Cauchy est un type spécial de Répartition de rapport.
- Leur produit
- Si
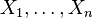 sont des variables normales standard indépendantes, puis
sont des variables normales standard indépendantes, puis  a une distribution chi-carré avec n degrés de liberté.
a une distribution chi-carré avec n degrés de liberté.
La normalisation des variables aléatoires normales
Du fait de la propriété 1, il est possible de relier ensemble des variables aléatoires normales à la normale standard.
Si 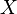 ~
~  , Puis
, Puis
est une variable aléatoire normale standard: 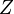 ~
~  . Une conséquence importante est que la fonction de répartition d'une distribution normale générale est donc
. Une conséquence importante est que la fonction de répartition d'une distribution normale générale est donc
Inversement, si 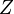 est une distribution normale standard,
est une distribution normale standard, 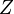 ~
~  , Puis
, Puis
est une variable aléatoire normale de moyenne  et la variance
et la variance  .
.
La distribution normale standard a été totalisées (généralement sous la forme de la valeur de la distribution cumulative fonction Φ), et les autres distributions normales sont les transformations simples, comme décrit ci-dessus, d'une norme. Par conséquent, on peut utiliser les valeurs des tables de la fonction de répartition de la distribution normale standard pour trouver les valeurs de la fonction de répartition d'une distribution normale général.
Moments
Les premières des moments de la distribution normale sont:
| Nombre | Raw instant | Moment central | Cumulant |
|---|---|---|---|
| 0 | 1 | 1 | |
| 1 |  | 0 |  |
| 2 |  |  |  |
| 3 |  | 0 | 0 |
| 4 |  |  | 0 |
| 5 |  | 0 | 0 |
| 6 | 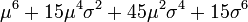 |  | 0 |
| 7 |  | 0 | 0 |
| 8 |  |  | 0 |
Tous cumulants de la distribution normale-delà de la seconde sont nuls.
Moments centraux plus élevés (de l'ordre 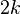 avec
avec 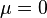 ) Peut être obtenu en utilisant la formule
) Peut être obtenu en utilisant la formule
![E \ left [x ^ {2k} \ right] = \ frac {(2k)!} {2 ^ kk!} \ Sigma ^ {} 2k.](../../images/109/10941.png)
Générer des valeurs pour les variables aléatoires normales
Pour les simulations sur ordinateur, il est souvent utile pour générer des valeurs qui ont une distribution normale. Il existe plusieurs méthodes et le plus fondamental est d'inverser la fonction de répartition normale standard. Des méthodes plus efficaces sont également connus, une telle méthode étant la Box-Muller transformer. Un algorithme encore plus rapide est le algorithme de ziggourat.
L'algorithme de Box-Muller dit que, si vous avez deux nombres a et b réparties uniformément sur (0, 1], (par exemple la sortie d'un générateur de nombres aléatoires), puis deux variables aléatoires standards normalement distribués sont c et d, où:
Ce est parce que la distribution du chi carré avec deux degrés de liberté (voir la propriété 4 ci-dessus) est une variable aléatoire exponentielle facilement généré.
Le théorème central limite

Dans certaines conditions (comme être indépendants et identiquement distribués de variance finie), la somme d'un grand nombre de variables aléatoires est normalement distribué environ - ce est le théorème central limite.
L'importance pratique du théorème de la limite centrale est que la fonction de distribution normale cumulative peut être utilisée comme une approximation pour d'autres fonctions de distribution cumulative, par exemple:
- Une loi binomiale de paramètres n et p est approximativement normale pour les grands n et p pas trop près de 1 ou 0 (certains livres vous recommandons d'utiliser cette approximation que si np et n (1 - p) sont à la fois au moins 5; dans ce cas, une correction de continuité doit être appliqué).
La distribution normale approximation a des paramètres μ = np, σ 2 = np (1 - p).
- Une distribution de Poisson de paramètre λ est à peu près normale pour les grands λ.
La distribution normale d'approximation des paramètres μ a = σ 2 = λ.
Que ces approximations sont suffisamment précise dépend de l'usage auquel ils sont nécessaires, et le taux de convergence de la distribution normale. Ce est généralement le cas que ces approximations sont moins précises dans les queues de la distribution. Un supérieur général lié de l'erreur d'approximation de la fonction de distribution cumulative est donnée par la Théorème de Berry-Esséen.
Infinie divisibilité
Les distributions normales sont infiniment divisibles distributions de probabilité: Étant donné une moyenne μ, une variance σ 2 ≥ 0, et un nombre naturel n, la somme X + 1. . . + X n de n variables aléatoires indépendantes
a cette distribution normale spécifiée (pour vérifier cela, l'utilisation ou fonctions caractéristiques convolution et induction mathématique).
Stabilité
Les distributions normales sont strictement distributions de probabilité stables.
Intervalles de rectification et de confiance standard

Environ 68% des valeurs tirées d'une distribution normale sont à moins d'un écart-type σ de> 0 loin de la moyenne μ; environ 95% des valeurs sont à deux écarts-types et environ 99,7% se situent dans trois écarts-types. Ceci est connu comme le " Règle 68-95-99.7 "ou la" règle empirique. "
Pour être plus précis, l'aire sous la courbe en cloche entre μ - n σ et μ + n σ en termes de la fonction de distribution normale cumulative est donnée par
où erf est la fonction d'erreur. Pour 12 décimales, les valeurs de la 1-, 2-, jusqu'à des points 6-sigma sont:
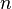 | 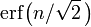 |
|---|---|
| 1 | ,682689492137 |
| 2 | ,954499736104 |
| 3 | ,997300203937 |
| 4 | ,999936657516 |
| 5 | ,999999426697 |
| 6 | ,999999998027 |
Le tableau suivant donne la relation inverse de multiples sigma correspondant à quelques valeurs souvent utilisées pour l'aire sous la courbe en cloche. Ces valeurs sont utiles pour déterminer (asymptotique) intervalles de confiance des niveaux spécifiés pour normalement distribués (ou asymptotiquement normal) estimateurs:
 | 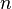 |
|---|---|
| 0,80 | 1,28155 |
| 0,90 | 1,64485 |
| 0,95 | 1,95996 |
| 0,98 | 2,32635 |
| 0,99 | 2,57583 |
| 0,995 | 2,80703 |
| 0,998 | 3,09023 |
| 0,999 | 3,29052 |
où la valeur du côté gauche de la table est la proportion de valeurs qui tombent dans un intervalle donné, et n est un multiple de l'écart-type définissant la largeur de l'intervalle.
Formulaire de famille exponentielle
La distribution normale est une à deux paramètres formulaire de famille exponentielle naturelle avec des paramètres μ et 1 / σ 2, et des statistiques naturelles X et X 2. La forme canonique a paramètres  et
et 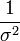 et statistiques suffisantes,
et statistiques suffisantes, 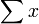 et
et  .
.
Processus gaussien complexe
Considérez variable aléatoire gaussienne complexe,
où X et Y sont des variables réelles et indépendantes gaussiennes ayant des variances égales  . Le pdf des variables communes est alors
. Le pdf des variables communes est alors
Parce que 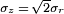 , Le PDF résultant pour le complexe gaussien variables Z est
, Le PDF résultant pour le complexe gaussien variables Z est
Distributions connexes
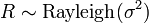 est un Distribution de Rayleigh si
est un Distribution de Rayleigh si  où
où  et
et  sont deux distributions normales indépendantes.
sont deux distributions normales indépendantes. 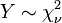 est une distribution chi-carré avec
est une distribution chi-carré avec 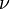 degrés de liberté si
degrés de liberté si  où
où 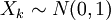 pour
pour  et sont indépendants.
et sont indépendants. 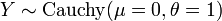 est un Distribution de Cauchy si
est un Distribution de Cauchy si  pour
pour 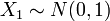 et
et  sont deux distributions normales indépendantes.
sont deux distributions normales indépendantes.  est un la distribution log-normale si
est un la distribution log-normale si  et
et  .
. - Rapport à La distribution alpha-stable biais Lévy: si
 puis
puis  .
.
- Distribution normale tronquée. Si
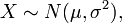 puis tronquer X ci-dessous au
puis tronquer X ci-dessous au 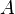 et au-dessus
et au-dessus  conduira à une variable aléatoire de moyenne
conduira à une variable aléatoire de moyenne 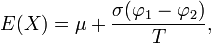 où
où  et
et  est le fonction de densité de probabilité d'une variable aléatoire normale standard.
est le fonction de densité de probabilité d'une variable aléatoire normale standard.
- Si
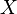 est une variable aléatoire avec une distribution normale, et
est une variable aléatoire avec une distribution normale, et 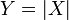 , Puis
, Puis 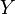 a un pliée distribution normale.
a un pliée distribution normale.
Les statistiques descriptives et inférentielles
Partitions
Beaucoup de points sont dérivées de la distribution normale, y compris rangs centiles («percentiles»), Les équivalents de courbe normale, stanines, z-scores, et T-score. En outre, un certain nombre de comportements statistiques procédures sont fondées sur l'hypothèse que les scores sont normalement distribués; par exemple, des t-tests et Des analyses de variance (voir ci-dessous). Bell a courbe classement attribue notes relatives basées sur une distribution normale des scores.
Tests de normalité
Tests de normalité vérifier un ensemble donné de données pour similitude avec la distribution normale. Le hypothèse nulle est que l'ensemble de données est similaire à la distribution normale, donc suffisamment faible P-valeur indique que les données non-normales.
- Test de Kolmogorov-Smirnov
- Test de Lilliefors
- Test d'Anderson-Darling
- Test Ryan-Joiner
- Test de Shapiro-Wilk
- Tracé de probabilité normale ( Rankit parcelle)
- Test de Jarque-Bera
Estimation des paramètres
Maximum de vraisemblance des paramètres
Supposer
sont indépendante et chacun est normalement distribué avec espérance μ et de variance σ ²> 0. Dans le langage des statisticiens, les valeurs observées de ces variables aléatoires n forment un "échantillon de taille n à partir d'une population distribuée normalement." Il est souhaitable d'estimer la «population signifie" μ et la «écart type de population», σ, basées sur les valeurs observées de cet échantillon. La fonction de densité de probabilité conjointe continue de ces variables aléatoires indépendantes est n
En fonction de μ et σ, la fonction de vraisemblance sur la base des observations X 1, ..., X n est
avec une constante C> 0 (qui, en général serait même permis de dépendre de X 1, ..., X n, mais disparaîtront de toute façon quand dérivées partielles de la fonction de log-vraisemblance par rapport aux paramètres sont calculés, voir ci-dessous ).
Dans le procédé de maximum de vraisemblance, les valeurs de μ et σ qui maximisent la fonction de vraisemblance sont pris comme des estimations de la population paramètres μ et σ.
Habituellement à maximiser une fonction de deux variables, on pourrait envisager dérivées partielles. Mais ici, nous allons exploiter le fait que la valeur de μ qui maximise la fonction de vraisemblance avec σ fixe ne dépend pas de σ. Par conséquent, nous pouvons constater que la valeur de μ, puis substituer à μ dans la fonction de vraisemblance, et enfin trouver la valeur de σ qui maximise l'expression résultante.
Il est évident que la fonction de vraisemblance est une fonction décroissante de la somme
Donc, nous voulons la valeur de μ qui minimise cette somme. Laisser
être la "moyenne de l'échantillon" sur la base des observations n. Observez que
Seul le dernier terme dépend de μ et il est minimisé par
Ce est l'estimation du maximum de vraisemblance de μ en fonction des n observations X 1, ..., X n. Lorsque nous substituons cette estimation pour μ dans la fonction de vraisemblance, nous obtenons
Il est classique pour désigner la fonction "log-likelihood", ce est à dire le logarithme de la fonction de vraisemblance, par un minuscule 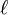 , Et nous avons
, Et nous avons
et puis
Ce dérivé est positive, nulle ou négative selon que σ ² est entre 0 et
ou égale à cette quantité, ou supérieure à cette quantité. (Si il ya juste une observation, ce qui signifie que n = 1, ou si X = 1 ... n = X, qui ne arrive avec une probabilité zéro, 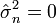 par cette formule, ce qui reflète le fait que, dans ces cas, la fonction de vraisemblance ne est pas borné comme σ diminue à zéro.)
par cette formule, ce qui reflète le fait que, dans ces cas, la fonction de vraisemblance ne est pas borné comme σ diminue à zéro.)
En conséquence de cette moyenne des carrés des résidus est l'estimation du maximum de vraisemblance de σ ², et sa racine carrée est l'estimation du maximum de vraisemblance de σ sur la base des n observations. Cet estimateur  est sollicité, mais a un plus petit l'erreur quadratique moyenne de l'estimateur sans biais d'habitude, qui est n / (n - 1) fois cet estimateur.
est sollicité, mais a un plus petit l'erreur quadratique moyenne de l'estimateur sans biais d'habitude, qui est n / (n - 1) fois cet estimateur.
Généralisation Surprenant
Le calcul de l'estimateur du maximum de vraisemblance de la matrice de covariance d'un distribution normale multivariée est subtile. Il se agit de la théorème spectral et la raison, il peut être préférable de voir un scalaire comme le trace d'un 1 × 1 matrice que comme un simple scalaire. Voir estimation des matrices de covariance.
Impartiale estimation des paramètres
L'estimateur du maximum de vraisemblance de la moyenne de population  à partir d'un échantillon est un estimateur non biaisé de la moyenne, comme ce est la variance lorsque la moyenne de la population est connu a priori. Cependant, si nous sommes confrontés à un échantillon et ne ont aucune connaissance de la moyenne ou la variance de la population dont il est tiré, l'estimateur sans biais de la variance
à partir d'un échantillon est un estimateur non biaisé de la moyenne, comme ce est la variance lorsque la moyenne de la population est connu a priori. Cependant, si nous sommes confrontés à un échantillon et ne ont aucune connaissance de la moyenne ou la variance de la population dont il est tiré, l'estimateur sans biais de la variance  est:
est:
Cette «variance de l'échantillon" suit une Distribution Gamma si tous les X i sont indépendants et identiquement distribués:
Occurrence
Environ distributions normales se produisent dans de nombreuses situations, en raison de la théorème central limite. Lorsqu'il existe des raisons de soupçonner la présence d'un grand nombre de petits effets qui agissent de façon additive et indépendamment, il est raisonnable de supposer que les observations seront normaux. Il existe des méthodes statistiques pour tester empiriquement cette hypothèse, par exemple, le Test de Kolmogorov-Smirnov.
Les effets peuvent aussi agir comme multiplicateurs modifications (plutôt que additifs). Dans ce cas, l'hypothèse de normalité ne est pas justifiée, et ce est le logarithme de la variable d'intérêt qui est normalement distribué. La distribution de la variable directement observé est alors appelé log-normale.
Enfin, se il ya une seule influence extérieure qui a un grand effet sur la variable à l'étude, l'hypothèse de normalité ne est pas justifié non plus. Ce est vrai même si, lorsque la variable externe est maintenue constante, les distributions marginales résultant sont en effet normal. La distribution complète sera une superposition de variables normales, qui ne est pas en général normale. Ceci est lié à la théorie des erreurs (voir ci-dessous).
Pour résumer, voici une liste des situations où la normalité approximative suppose parfois. Pour une discussion plus approfondie, voir ci-dessous.
- Dans les problèmes de comptage (de sorte que le théorème central limite comprend une approximation discrète à continuum) où variables aléatoires de reproduction sont impliqués, tels que
- Variables aléatoires binomiales , associés aux questions oui / non;
- Variables aléatoires de Poisson , associée à des événements rares;
- Dans les mesures physiologiques de spécimens biologiques:
- Le logarithme de mesures de la taille des tissus vivants (longueur, hauteur, surface de la peau, poids);
- La longueur des appendices inertes (cheveux, les ongles, les griffes, dents) des échantillons biologiques, dans la direction de la croissance; sans doute l'épaisseur de l'écorce d'arbre tombe également dans cette catégorie;
- Autres mesures physiologiques peuvent être distribuées normalement, mais il n'y a aucune raison de se attendre à ce que, a priori;
- Les erreurs de mesure sont souvent supposées être distribuées normalement, et tout écart par rapport à la normalité est considéré comme quelque chose qui doit être expliqué;
- Les variables financières
- Les changements dans le logarithme des taux de change, les indices des prix, et les indices boursiers; ces variables se comportent comme l'intérêt composé, pas comme un intérêt simple, et sont donc multiplicatif;
- Autres variables financières peuvent être distribuées normalement, mais il n'y a aucune raison de se attendre à ce que, a priori;
- L'intensité lumineuse
- L'intensité de la lumière laser est normalement distribué;
- La lumière thermique a une La distribution de Bose-Einstein sur des échelles de temps très courts, et une distribution normale sur des échéances plus longues en raison de la théorème central limite.
De l'intérêt pour la biologie et de l'économie est le fait que les systèmes complexes ont tendance à afficher lois de puissance plutôt que la normalité.
Comptage de photons
L'intensité lumineuse d'une source unique varie avec le temps, que les fluctuations thermiques peuvent être observées si la lumière est analysée avec une résolution de temps suffisamment élevé. L'intensité est généralement supposé être normalement distribués. La mécanique quantique interprète mesures de l'intensité de lumière photon comptage. L'hypothèse naturelle dans ce cadre est la distribution de Poisson . Lorsque l'intensité lumineuse est intégrée sur fois plus longtemps que le temps de cohérence et est grand, la limite de Poisson-à-normale est approprié.
Les erreurs de mesure
La normalité est l'hypothèse centrale de la mathématique théorie des erreurs. De même, dans le modèle statistique raccord, un indicateur de qualité de l'ajustement est que le résidus (comme les erreurs sont appelés dans ce cadre) soient indépendants et distribués normalement. L'hypothèse est que tout écart par rapport à la normalité doit être expliqué. En ce sens, à la fois dans le modèle ajusté et dans la théorie des erreurs, la normalité est la seule observation qui ne doivent pas être expliqué, étant prévu. Toutefois, si les données d'origine ne sont pas normalement distribuées (par exemple se ils suivent une Cauchy distribution), les résidus ne seront pas également distribuées normalement. Ce fait est généralement ignoré dans la pratique.
Des mesures répétées de la même quantité devraient donner des résultats qui sont regroupés autour d'une valeur particulière. Si toutes les sources principales d'erreurs ont été prises en compte, il est supposé que l'erreur restante doit être le résultat d'un grand nombre de très petites additifs effets, et donc normal. Les écarts à la normalité sont interprétées comme des indications d'erreurs systématiques qui ne sont pas prises en compte. Si cette hypothèse est valable est discutable. Une remarque célèbre et souvent citée attribué à Gabriel Lippmann dit: «Tout le monde croit en la loi [normale] d'erreurs: les mathématiciens, parce qu'ils pensent qu'il est un fait expérimental, et les expérimentateurs, parce qu'ils supposent qu'il est un théorème de mathématiques ».
Les caractéristiques physiques des échantillons biologiques
Les tailles des animaux adultes est d'environ log-normale. La preuve et une explication basée sur les modèles de croissance a été publié la première fois en 1932 le livre problèmes de croissance relative par Julian Huxley.
Les différences de taille en raison de dimorphisme sexuel, ou d'autres polymorphismes comme le travailleur / soldat / division reine chez les insectes sociaux, font en outre la distribution des tailles dévier de lognormalité.
L'hypothèse selon laquelle la taille linéaire d'échantillons biologiques est normal (plutôt que log-normale) conduit à une distribution non normale des poids (puisque le poids ou le volume est à peu près proportionnelle à la 2ème ou 3ème puissance de longueur, et les distributions gaussiennes ne sont conservés par des transformations linéaires ), et inversement en supposant que le poids est conduit normales à des longueurs non-normales. Ceci est un problème, car il n'y a pas a priori de raison pour laquelle on la longueur ou la masse corporelle, et pas l'autre, devrait être distribué normalement. Distributions lognormales, d'autre part, sont conservés par les puissances de sorte que le «problème» disparaît si lognormalité est supposé.
D'autre part, il ya quelques mesures biologiques où la normalité est supposé, comme la pression artérielle d'êtres humains adultes. Cela est censé être normalement distribué, mais seulement après avoir séparé les mâles et les femelles dans différentes populations (dont chacun est normalement distribué).
Les variables financières
Déjà en 1900 Louis Bachelier proposé représentant des variations de prix des actions à l'aide de la distribution normale. Cette approche a depuis été légèrement modifié. En raison de la nature exponentielle de l'inflation , les indicateurs financiers tels que les actions et les valeurs des matières premières les prix présentent "un comportement multiplicatif". En tant que tel, leurs changements périodiques (par exemple, les changements annuels) ne sont pas normaux, mais plutôt lognormale - c.-à- retours par opposition aux valeurs sont normalement distribués. Ceci est encore l'hypothèse la plus couramment utilisée dans la finance , en particulier dans l'évaluation des actifs. Corrections apportées à ce modèle semblent être nécessaires, comme cela a été souligné par exemple par Benoît Mandelbrot, le vulgarisateur de fractales , qui a observé que les changements dans logarithme sur de courtes périodes (comme un jour) sont bien approchées par des distributions qui ne disposent pas variance finie, et donc le théorème central limite ne sont pas applicables. Plutôt, la somme de beaucoup de ces changements donne distributions log-Levy.
Répartition dans les tests et l'intelligence
Parfois, la difficulté et le nombre de questions sur un test de QI est sélectionné afin de donner des résultats distribués normales. Ou bien, les résultats des tests premières sont converties en valeurs de QI par leur adaptation à la distribution normale. Dans les deux cas, il est le résultat délibéré de la construction d'essai ou marquer interprétation qui mène à des scores de QI étant distribuées normalement pour la majorité de la population. Cependant, la question de savoir si l'intelligence elle-même est normalement distribué est plus complexe, car l'intelligence est une variable latente, donc sa distribution ne peut être observée directement.
équation de diffusion
La fonction de densité de probabilité de la distribution normale est étroitement liée à la (homogène et isotrope)équation de diffusion et donc également à la équation de la chaleur.Cetteéquation différentielle partielledécrit l'évolution dans le temps d'une fonction de masse de densité sous diffusion.En particulier, la fonction de densité de probabilité
pour la distribution normale avec valeur 0 et de variance attendustsatisfait l'équation de diffusion:
Si la masse densité au moment t = 0 est donnée par un Dirac, ce qui signifie essentiellement que toute la masse est d'abord concentré en un seul point, alors la fonction de masse densité au moment t aura la forme de la fonction normale de densité de probabilité avec une variance croissante linéairement avec t . Cette connexion est pas un hasard: la diffusion est due à un mouvement brownien qui est mathématiquement décrite par un processus de Wiener, et un tel processus au moment t se traduira également par une distribution normale avec une variance croissante linéairement avec t .
Plus généralement, si la masse-densité initiale est donnée par une fonction φ (x), puis la masse densité au momenttsera donnée par laconvolution de φ et une fonction normale de densité de probabilité.
Approximations numériques de la distribution normale et son cdf
La distribution normale est largement utilisé dans le calcul scientifique et statistique. Par conséquent, il a été mis en œuvre de diverses manières.
Le GNU Scientific Library calcule les valeurs de la fonction de répartition normale standard en utilisant des approximations par morceaux en fonctions rationnelles. Une autre méthode d'approximation utilise des polynômes du troisième degré sur des intervalles . L'article sur le langage de programmation de la Colombie-Britannique donne un exemple de la façon de calculer la cdf dans GNU bc.
Génération d'écarts de l'unité normale se fait normalement en utilisant la méthode de Box-Muller de choisir un angle uniforme et un rayon exponentielle puis transformer à (normalement distribué) x et y coordonnées. Si journaux, cos ou le péché sont chers alors une alternative simple est de simplement résumer 12 uniforme (0,1) et écarte soustraire 6 (la moitié de 12). Ceci est tout à fait utilisable dans de nombreuses applications. La somme de plus de 12 valeurs est choisi car cela donne un écart d'exactement un. Le résultat est limité à la plage (-6,6) et a une densité qui est un 12-section onzième ordre approximation polynomiale à la distribution normale.
Une méthode qui est beaucoup plus rapide que la Box-Muller transformer, mais qui est encore exacte est le soi-disant algorithme Ziggurat développé par George Marsaglia. Dans environ 97% de tous les cas, il utilise seulement deux nombres aléatoires, un entier aléatoire et un uniforme aléatoire, une multiplication et un test, si. Seulement dans 3% des cas où la combinaison de ces deux chutes à l'extérieur du "noyau de la ziggourat" une sorte de rejet d'échantillonnage en utilisant les logarithmes, exponentielles et des nombres aléatoires plus uniformes doit être employé.
Il ya aussi quelques recherches sur le lien entre le jeûne Hadamard transformer et la distribution normale depuis le transformer emploie un peu addition et la soustraction et par les théorème de la limite des nombres aléatoires centrales de presque toute distribution sera transformé en la distribution normale. A cet égard, une série de transformées de Hadamard peut être combiné avec des permutations aléatoires pour activer des ensembles de données arbitraires dans un ensemble de données à distribution normale.
En Microsoft Excel la fonction NORMSDIST () calcule la fonction de répartition de la distribution normale standard, et NORMSINV () calcule sa fonction inverse. Par conséquent, NORMSINV (RAND ()) est une façon précise mais lente de générer des valeurs de la distribution normale standard, en utilisant le principe de la transformation inverse échantillonnage.
Bagatelles
- La dernière série de10 billets en deutsche marks en vedetteCarl Friedrich Gausset un graphique et la formule de la fonction normale de densité de probabilité.



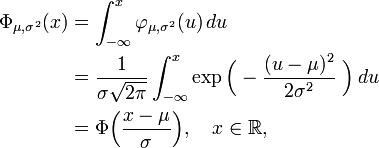

![\ Phi (x) = \ frac {1} {2} \ Bigl [1 + \ {operatorname erf} \ Bigl (\ frac {x} {\ sqrt {2}} \ bigr) \ bigr], \ quad x \ dans \ mathbb {R},](../../images/108/10890.png)
![\ Phi _ {\ mu, \ sigma ^ 2} (x) = \ frac {1} {2} \ Bigl [1 + \ {operatorname erf} \ Bigl (\ frac {x \ mu} {\ sigma \ sqrt { 2}} \ bigr) \ bigr], \ quad x \ in \ mathbb {R}.](../../images/108/10891.png)
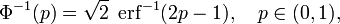
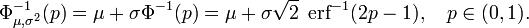



![\ Begin {align} m_x (t) et {} = \ mathrm {E} \ left [\ {exp (TX)} \ right] \\ & {} = \ int _ {- \ infty} ^ {\ infty} \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp {\ left (- \ frac {(x - \ mu) ^ 2} {2 \ sigma ^ 2} \ right)} \ {exp (tx )} \, dx \\ & {} = \ exp {\ left (\ mu t + \ frac {\ sigma ^ 2 t ^ 2} {2} \ right)} \ end {align}](../../images/109/10904.png)
![\ Begin {align} \ chi_X (t; \ mu, \ sigma) et {} = m_x (it) = \ mathrm {E} \ left [\ exp (ce X) \ right] \\ & {} = \ int_ {- \ infty} ^ {\ infty} \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp \ gauche (- \ frac {(x - \ mu) ^ 2} {2 \ sigma ^ 2 } \ right) \ exp (itx) \, dx \\ & {} = \ exp \ left (i \ mu t - \ frac {\ sigma ^ 2 t ^ 2} {2} \ right). \ End {align}](../../images/109/10907.png)