Géométrie analytique
À propos de ce écoles sélection Wikipedia
Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?
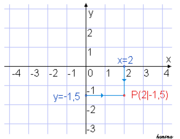
Géométrie analytique, aussi appelé la géométrie des coordonnées mentionnée précédemment que la géométrie cartésienne ou la géométrie analytique, est l'étude de la géométrie en utilisant les principes de l'algèbre . Que l'algèbre des nombres réels peut être utilisé pour produire des résultats sur le continuum de la géométrie linéaire repose sur la Axiome Cantor-Dedekind. Habituellement, le système de coordonnées cartésiennes est appliqué à manipuler des équations pour les avions , lignes, des lignes droites et carrés , souvent en deux et parfois en trois dimensions de mesure. Comme enseigné dans les manuels scolaires, la géométrie analytique peut se expliquer plus simplement: il est préoccupé par la définition des formes géométriques de manière numérique et extraire des informations numériques de cette représentation. La sortie numérique, cependant, peut aussi être un vecteur ou un façonner. Certains considèrent que l'introduction de la géométrie analytique est le début de modernes des mathématiques .
Histoire
Le mathématicien grec Ménechme résolu des problèmes et a prouvé théorèmes en utilisant une méthode qui avait une forte ressemblance avec l'utilisation de coordonnées et il a parfois soutenu qu'il avait la géométrie analytique. Apollonius de Perge, dans Sur la section Déterminé traité des problèmes d'une manière qui peut être appelé une géométrie analytique d'une dimension; la question de trouver des points sur une ligne qui se trouvaient dans un rapport aux autres. Apollonios dans les coniques développé une méthode qui est très similaire à la géométrie analytique que son travail est parfois pensé pour avoir anticipé le travail de Descartes par quelques 1800 années. Son application des lignes de référence, un diamètre et une tangente a pratiquement pas différente de celle de notre utilisation moderne d'un système de coordonnées, où les distances mesurées le long du diamètre du point de tangence sont les abscisses, et les segments parallèles à la tangente et interceptée entre l'axe et la courbe sont les ordonnées. Il a développé davantage les relations entre les abscisses et les ordonnées correspondantes qui sont équivalentes aux équations rhétoriques de courbes. Cependant, bien que Apollonius est venu près de développer la géométrie analytique, il n'a pas réussi à le faire car il ne tient pas compte des grandeurs négatives et dans tous les cas le système de coordonnées a été superposée sur une courbe donnée a posteriori au lieu d'a priori. Ce est, équations ont été déterminés par des courbes, mais les courbes ne ont pas été déterminées par des équations. Coordonnées, variables et équations étaient notions subsidiaires appliqués à une situation géométrique spécifique.
Le XIe siècle Persique mathématicien Omar Khayyam a vu une forte relation entre la géométrie et de l'algèbre, et se déplaçait dans la bonne direction quand il a aidé à combler le fossé entre l'algèbre numérique et géométrique avec sa solution géométrique de la générale équations cubiques, mais le pas décisif est venu plus tard avec Descartes.
Géométrie analytique a été traditionnellement attribuée à René Descartes qui a fait des progrès significatifs dans les méthodes de la géométrie analytique lorsque IN 1637 dans l'annexe intitulée Géométrie du discours intitulé sur la méthode pour bien conduire sa raison dans la recherche de la vérité dans les sciences, communément appelé Discours de la Méthode. Cet ouvrage, écrit dans son pays natal français langue, et ses principes philosophiques, a fourni la base pour le calcul en Europe.
Abraham de Moivre également pionnier dans le développement de la géométrie analytique. Avec l'hypothèse de la Cantor-Dedekind axiome, la géométrie euclidienne est essentiellement que interprétable dans la langue de la géométrie analytique (ce est-à chaque théorème de l'un est un théorème de l'autre), La preuve de Alfred Tarski du décidabilité du champ réel ordonné pourrait être considéré comme une preuve que la géométrie euclidienne est cohérente et décidable.
Thèmes
Thèmes importants de la géométrie analytique sont
- espace vectoriel
- définition de l' avion
- la distance problèmes
- la produit scalaire, pour obtenir l'angle de deux vecteurs
- le produit en croix , pour obtenir un vecteur perpendiculaire de deux vecteurs connus (et aussi leur volume spatial)
- intersection problèmes
Beaucoup de ces problèmes concernent l'algèbre linéaire .
Exemple
Voici un exemple d'un problème de la États-Unis d'Amérique mathématique Talent Search qui peut être résolu par la géométrie analytique:
Problème: Dans un pentagone convexe 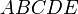 Dont les côtés ont des longueurs
Dont les côtés ont des longueurs 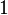 ,
,  ,
,  ,
,  Et
Et 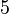 , Bien que non nécessairement dans cet ordre. Laisser
, Bien que non nécessairement dans cet ordre. Laisser 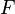 ,
, 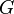 ,
,  Et
Et 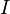 sont les milieux des côtés
sont les milieux des côtés 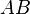 ,
, 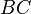 ,
, 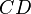 Et
Et  Respectivement. Laisser
Respectivement. Laisser 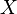 le milieu du segment
le milieu du segment  Et
Et 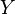 le milieu du segment
le milieu du segment 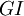 . La longueur du segment
. La longueur du segment 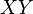 est un nombre entier. Trouver toutes les valeurs possibles de la longueur du côté
est un nombre entier. Trouver toutes les valeurs possibles de la longueur du côté  .
.
Solution: Laissez  ,
,  ,
, 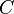 ,
,  Et
Et  être situé à
être situé à  ,
,  ,
, 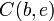 ,
, 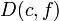 Et
Et  .
.
En utilisant le formule du point milieu, les points 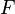 ,
, 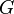 ,
,  ,
, 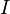 ,
, 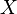 Et
Et 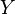 sont situés à
sont situés à
 ,
, 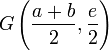 ,
, 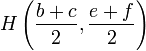 ,
,  ,
, 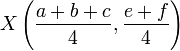 Et
Et 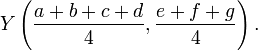
Utilisation de la distance de la formule,
et
Depuis 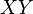 doit être un nombre entier ,
doit être un nombre entier ,
(Voir arithmétique modulaire ) afin 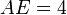 .
.
D'autres utilisations
Géométrie analytique, pour géomètres algébriques, est aussi le nom de la théorie de (réel ou) variétés complexes et les espaces analytiques plus généraux définis localement par la disparition de fonctions analytiques de plusieurs variables complexes (ou parfois vrais). Elle est étroitement liée à la géométrie algébrique, notamment à travers le travail de Jean-Pierre Serre GAGA.