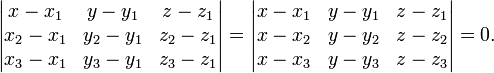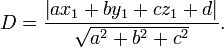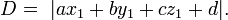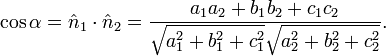Avion (géométrie)

Renseignements généraux

SOS Enfants produite ce site pour les écoles ainsi que ce site de vidéo sur l'Afrique . SOS Enfants a regardé des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?

Deux plans se coupant dans l'espace à trois dimensions

En mathématiques , un avion est un bidimensionnelle collecteur ou surface qui est parfaitement plat. Officieusement, il peut être considéré comme une feuille infiniment vaste et infiniment mince orientée dans certains espace. Formellement, ce est un espace affine de dimension deux.

Lorsque l'on travaille dans l'espace euclidien à deux dimensions, l'article défini est utilisé, l'avion, de se référer à tout l'espace. De nombreuses tâches fondamentales dans la géométrie , la trigonométrie et graphique sont effectuées dans l'espace à deux dimensions, ou en d'autres termes, dans le plan. Beaucoup des mathématiques peut être et a été réalisée dans le plan, notamment dans les domaines de la géométrie , la trigonométrie , théorie des graphes et graphique.

La géométrie euclidienne

Dans l'espace euclidien un avion est un surface de telle sorte que, compte tenu de toute deux distincte points de la surface, la surface contient également les uniques ligne droite qui passe par ces points.

La structure fondamentale de ces deux plans sera toujours le même. En mathématiques ce est décrit comme l'équivalence topologique . Officieusement cependant, cela signifie que les deux plans se ressemblent.

Un avion peut être déterminée uniquement par l'une des suivantes (ensembles de) objets:

trois points non alignés (ce est à dire, ne se trouvant sur la même ligne )
une ligne et un point non sur la ligne
deux lignes avec un point d'intersection
deux lignes parallèles

Avions intégrés dans R ³

Cette section concerne spécifiquement les avions embarqués en trois dimensions: précisément, dans ℝ ^3.

Propriétés

Dans l'espace euclidien à trois dimensions, nous pouvons exploiter les faits suivants qui ne détiennent pas de dimensions supérieures:

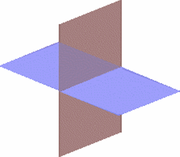
Deux avions sont soit parallèles, soit ils se croisent en ligne.
Une ligne est soit parallèle à un plan ou croise en un point unique ou est contenue dans le plan.
Deux lignes perpendiculaires à un même plan doivent être parallèles les uns aux autres.
Deux plans perpendiculaires à la même ligne doivent être parallèles les uns aux autres.

Définir un plan avec un point et un vecteur normal

Dans un espace à trois dimensions, un autre moyen important de définir un plan est en spécifiant un point et une vecteur normal au plan.

Laisser $\ P gras$ être le point que nous souhaitons trouver dans le plan, et laisser $\ Vec n$ un vecteur normal au plan différent de zéro. Le plan souhaité est l'ensemble de tous les points $\ R gras$ tel que $\ Vec n \ cdot (r- p gras \) = 0.$

Si nous écrivons 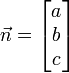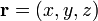$\ Vec n = \ begin {} bmatrix un \\ b \\ c \ end {} bmatrix$ , $\ R gras = (x, y, z)$ et d comme le produit scalaire 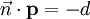$\ Vec n \ cdot \ p gras = -d$ , Puis l'avion 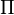$\ Pi$ est déterminée par la condition 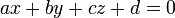$ax + by + cz + d = 0 \,$ , Où a, b, c et d sont des nombres réels et a, b et c ne sont pas tous nuls.

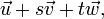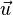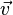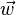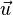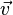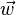Alternativement, un plan peut être décrit paramétrique que l'ensemble des points de la forme $\ Vec {u} + s \ vec {v} + t \ vec {w},$ où s et t plage sur tous les nombres réels, et $\ Vec {u}$ , $\ Vec {v}$ et $\ Vec {w}$ sont donnés vecteurs définissant le plan. $\ Vec {u}$ des points de l'origine à un point arbitraire sur le plan, et $\ Vec {v}$ et $\ Vec {w}$ peut être visualisé comme à partir de 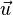$\ Vec {u}$ et pointant dans des directions différentes le long du plan. 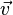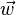$\ Vec {v}$ et $\ Vec {w}$ peut, mais ne ont pas à être perpendiculaire (mais ils ne peuvent pas être alignés).

Définir un plan passant par trois points

Le plan passant par trois points 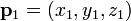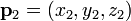$\ P_1 gras = (x 1, y_1, z_1)$ , $\ P_2 gras = (x_2, Y_2, Z_2)$ et $\ P_3 gras = (x_3, y_3, z_3)$ peut être défini comme l'ensemble des points (x, y, z) qui correspondent aux caractéristiques suivantes déterminants équations:

$\ Begin {} vmatrix x - x 1 et y - y_1 & z - z_1 \\ x_2 - x_1 & Y_2 - y_1 & Z_2 - z_1 \\ x_3 - x_1 & y_3 - y_1 & z_3 - z_1 \ end {} vmatrix = \ begin { vmatrix} x - x 1 et y - y_1 & z - z_1 \\ x - y x_2 & - Y_2 & z - Z_2 \\ x - y x_3 & - y_3 & z - z_3 \ end {} vmatrix = 0.$

Pour décrire le plan comme une équation sous la forme $ax + by + cz + d = 0$ , Résoudre le système d'équations suivant:

$\, Ax_1 + by_1 + cz_1 + d = 0$

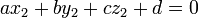
$\, Ax_2 + by_2 + cz_2 + d = 0$

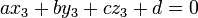$\, Ax_3 + by_3 + cz_3 + d = 0$ .

Ce système peut être résolu en utilisant Cramer règle et les manipulations de la matrice de base. Laisser 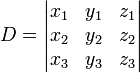$D = \ begin {} vmatrix x_1 & y_1 & z_1 \\ x_2 & Y_2 & Z_2 \\ x_3 & y_3 & z_3 \ end {} vmatrix$ . Ensuite,

$a = \ frac {} -d {D} \ begin {} vmatrix 1 & y_1 & z_1 \\ 1 & Y_2 & Z_2 \\ 1 & y_3 & z_3 \ end {} vmatrix$

$b = \ frac {} -d {D} \ begin {} vmatrix x_1 & 1 & z_1 \\ x_2 & 1 & Z_2 \\ x_3 & 1 & z_3 \ end {} vmatrix$

$c = \ frac {} -d {D} \ begin {} vmatrix x_1 & y_1 & 1 \\ x_2 & Y_2 & 1 \\ x_3 & y_3 & 1 \ end {} vmatrix$ .

Ces équations sont paramétrique d. Réglage d égal à ne importe quel nombre non nulle et son remplacement dans ces équations donnera un ensemble de solution.

Cet avion peut également être décrit par le "point et un vecteur normal" prescription ci-dessus.

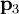Un vecteur approprié normale est donnée par la produit vectoriel $\ Vec n = (\ p_2 gras - p_1 \ gras) \ times (\ P_3 gras - p_1 \ gras),$ et le point $\ P gras$ peut être considéré comme étant l'un des points donnés $\ P_1 gras, \ p_2 gras$ ou $\ P_3 gras$ .

Distance d'un point à un plan

Pour un avion $\ Pi: ax + by + cz + d = 0 \,$ et un point 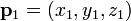$\ P_1 gras = (x 1, y_1, z_1)$ pas nécessairement se trouvant dans l'avion, la distance la plus courte à partir de $\ P_1 gras$ par rapport au plan est

$D = \ frac {\ left | a + b x_1 y_1 + c + d z_1 \ right |} {\ sqrt {a ^ 2 + b ^ 2 + c ^ 2}}.$

Il se ensuit que $\ P_1 gras$ située dans le plan si et seulement si D = 0.

Si $\ Sqrt {a ^ 2 + b ^ 2 + c ^ 2} = 1$ ce qui signifie que a, b et c sont normalisées alors l'équation devient

$D = \ | a + b x_1 y_1 + c + d z_1 |.$

Ligne d'intersection entre deux plans

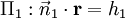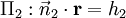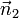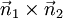Compte tenu des plans d'intersection décrites par $\ Pi_1: \ vec n_1 \ cdot \ r = gras h_1$ et $\ Pi_2: \ vec n_2 \ cdot \ r = gras H_2$ , La ligne d'intersection perpendiculaire à la fois $\ N_1 vec$ et $\ N_2 vec$ et donc parallèle à $\ Vec n_1 \ times \ vec n_2$ .

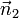Si nous supposons en outre que $\ N_1 vec$ et $\ N_2 vec$ sont orthonormée puis le point le plus proche sur la ligne d'intersection à l'origine est $\ Gras r_0 = h_1 \ n_1 vec + H_2 \ n_2 vec$ .

Dièdre

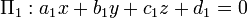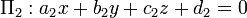Compte tenu des deux plans d'intersection décrites par $\ Pi_1: a_1 x + y + b_1 c_1 z + d_1 = 0 \,$ et $\ Pi_2: a_2 x + y + b_2 c_2 z + d_2 = 0 \,$ , Le angle dièdre entre eux est défini comme étant l'angle 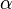$\ Alpha$ entre leurs directions normales:

$\ Cos \ alpha = \ hat n_1 \ cdot \ hat n_2 = \ frac {a_1 a_2 + b_1 b_2 + c_1 c_2} {\ sqrt {a_1 ^ 2 + b_1 ^ 2 + c_1 ^ 2} \ sqrt {a_2 ^ 2 + b_2 ^ 2 + c_2 ^ 2}}.$

Planes dans divers domaines des mathématiques

En plus de son familier géométrique la structure, avec isomorphismes qui sont isométries par rapport au produit intérieur habitude, le plan peut être consulté à divers autres niveaux de abstraction. Chaque niveau d'abstraction correspond à un particulier catégorie.

À un extrême, tout géométrique et concepts métriques peuvent être tombé à quitter le topologique avion, qui peut être considéré comme un idéalisée homotopiquement feuille de caoutchouc trivial infinie, qui conserve une notion de proximité, mais n'a pas de distances. Le plan topologique a un concept d'une trajectoire linéaire, mais pas de concept d'une ligne droite. Le plan topologique, ou son équivalent le disque ouvert, est le voisinage topologique de base utilisé pour construire surfaces (ou 2-variétés) classés dans topologie de basse dimension. Isomorphismes du plan topologique sont tous continu bijections. Le plan topologique est le cadre naturel pour la branche la théorie des graphes qui traite graphes planaires, et les résultats comme le Théorème des quatre couleurs .

L'avion peut également être considérée comme une espace affine, dont les isomorphismes sont des combinaisons de traductions et des cartes linéaires non singulières. De ce point de vue il n'y a pas de distances, mais colinéarité et des rapports de distance sur ne importe quelle ligne sont préservés.

Géométrie différentielle considère un plan comme un véritable deux dimensions collecteur , un plan topologique qui est pourvu d'un la structure différentielle. Encore une fois, dans ce cas, il n'y a pas de notion de la distance, mais il est maintenant un concept de finesse de cartes, par exemple un différentiables ou chemin lisse (selon le type de structure différentielle appliquée). Les isomorphismes dans ce cas sont bijections avec le degré de différentiabilité choisi.

Dans la direction opposée de l'abstraction, nous pouvons appliquer une structure de champ compatible avec le plan géométrique, donnant lieu à la plan complexe et la région majeure de analyse complexe. Le domaine complexe n'a que deux isomorphismes qui quittent la ligne réelle fixé, l'identité et conjugaison.

De la même manière que dans le cas réel, le plan peut également être considérée comme la plus simple, une dimension (sur les nombres complexes) variété complexe, parfois appelé la ligne complexe. Toutefois, ce point de vue contraste avec le cas de l'avion comme une véritable collecteur deux dimensions. Les isomorphismes sont tous bijections conforme du plan complexe, mais les seules possibilités sont les cartes qui correspondent à la composition d'une multiplication par un nombre complexe et d'une traduction.

En outre, la géométrie euclidienne (qui a zéro courbure partout) ne est pas la seule géométrie que l'avion peut avoir. Le plan peut être donné une géométrie sphérique en utilisant le projection stéréographique. Cela peut être considéré comme plaçant une sphère sur le plan (comme une balle sur le sol), en supprimant le point le plus haut, et en projetant la sphère sur le plan de ce point). Ce est l'une des saillies qui peuvent être utilisés dans la fabrication d'une carte à plat d'une partie de la surface de la Terre. La géométrie résultante a une courbure constante positive.

En variante, le plan peut également être donné une métrique qui lui donne une courbure négative constante permet de donner plan hyperbolique. Cette dernière possibilité trouve une application dans la théorie de la relativité restreinte dans le cas simplifié où il ya deux dimensions spatiales et une dimension temporelle. (Le plan hyperbolique est un type temps hypersurface en trois dimensions Espace de Minkowski.)

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Plane_(geometry)&oldid=197517431 "