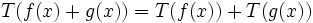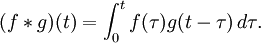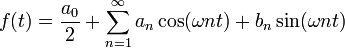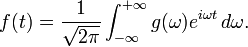Opérateur (mathématiques)

En mathématiques , un opérateur est une fonction , qui fonctionne sur (ou modifie) une autre fonction. Souvent, un "opérateur" est une fonction qui agit sur les fonctions pour produire d'autres fonctions (au sens où Oliver Heaviside a utilisé le terme); ou il peut être une généralisation d'une telle fonction, comme dans l'algèbre linéaire , où une partie de la terminologie reflète l'origine de l'objet à des opérations sur les fonctions qui sont des solutions d' équations différentielles . Un opérateur peut effectuer une fonction sur ne importe quel nombre des opérandes (entrées) mais le plus souvent il ya un seul opérande.

Un opérateur pourrait également être appelé un opération, mais le point de vue est différent. Par exemple, on peut dire "l'opération d'addition" (mais pas "l'opérateur d'addition") lors de la focalisation sur les opérandes et le résultat. On dit "opérateur d'addition" lorsqu'on se concentre sur le processus de l'addition, ou du point de vue plus abstrait, la fonction +: S × S → S.

Notation

Un nom d'opérateur ou le symbole de l'opérateur est une notation qui désigne un opérateur particulier. Quand il n'y a aucun risque de confusion, un nom d'opérateur ou le symbole de l'opérateur peuvent être renvoyés à plus brièvement comme un «opérateur». Strictement parlant, cependant, l'opérateur est un objet mathématique et non l'entité syntaxique qui dénote il. Le fait de relever avec sa notation est qu'il ya certains opérateurs qui sont venus à avoir notations standard.

Des exemples simples des opérateurs

En algèbre linéaire un «opérateur» est un opérateur linéaire. Dans l'analyse d'un "opérateur" peut être un opérateur différentiel, pour effectuer la différenciation ordinaire, ou un opérateur intégral, pour effectuer l'intégration ordinaire.

Un exemple est un opérateur différentiel, est le dérivé lui-même. Le nom de l'opérateur correspondant D, lorsqu'il est placé avant une fonction différentiable f, indique que la fonction est d'être différenciée par rapport à la variable.

Opérateurs par rapport fonctions

L'opérateur de mot peut en principe être appliquée à ne importe quelle fonction. Cependant, en pratique, il est le plus souvent appliquée à des fonctions qui agissent sur mathématique entités de complexité plus élevé que les nombres réels , comme des vecteurs , des variables aléatoires , ou expressions mathématiques. Le différentiel et opérateurs intégraux, par exemple, ont domaines et codomaines dont éléments sont des expressions mathématiques de complexité indéterminée. En revanche, les fonctions avec des domaines de valeurs vectorielles, mais gammes scalaires sont appelés fonctionnelles et formes.

En général, si le nom de domaine soit ou codomaine (ou les deux) de fonction contient des éléments beaucoup plus complexe que les nombres réels, cette fonction est appelée un opérateur. Inversement, si ni le nom de domaine ni le codomaine de fonction contiennent des éléments plus compliqués que les chiffres réels, cette fonction est susceptible d'être désigné simplement comme une fonction. Les fonctions trigonométriques telles que cosinus sont des exemples de ce dernier cas.

En outre, lorsque les fonctions sont utilisés si souvent qu'ils ont évolué notations rapide ou plus facile que le F (x, y, z, ...) forme générique, les formes particulières résultant sont aussi appelés opérateurs. Des exemples comprennent opérateurs infixes telles que l'addition "+" et la division "/", et postfix opérateurs tels que factorielle "!". Cet usage ne est pas liée à la complexité des entités impliquées.

Influences d'autres disciplines

Concepts d'autres disciplines, y compris dans la physique et à un degré moindre de l'informatique , ont influencé la façon dont les opérateurs sont perçus et utilisés.

Physique

L'influence mutuelle entre la physique et des mathématiques concernant le concept des opérateurs a été à long terme, en commençant dans les années 1900, et profonde dans les deux sens. La mécanique quantique en particulier a été contraint de passer de stratégies de mesure classiques impliquant des valeurs numériques simples à l'utilisation des opérateurs qui ont transformé et manipulés entités beaucoup moins intuitives. Ces inclus vecteurs à la fois dans l'espace réel et dans des généralisations de l'espace réel appelés Espaces de Hilbert, spineurs, et diverses formes de matrices . Le grand physicien Paul Dirac capturé l'importance de la relation entre la physique quantique et les mathématiques en disant "lois physiques devraient avoir la beauté mathématique et la simplicité."

Exemples d'opérateurs mathématiques

Cette section se concentre sur illustrant la puissance expressive de la notion d'opérateur en mathématiques. Se il vous plaît se référer aux sujets individuels pages pour plus de détails.

Opérateurs linéaires

Le type le plus commun de l'opérateur rencontré sont des opérateurs linéaires. En parlant opérateurs linéaires, l'opérateur est signifié généralement par les lettres T ou L. Les opérateurs linéaires sont ceux qui satisfont aux conditions suivantes; prendre l'opérateur T générale, la fonction a agi sur sous l'opérateur T, écrit f (x), et la constante a:

De nombreux opérateurs sont linéaires. Par exemple, l'opérateur différentiel et exploitant de Laplace, que nous verrons plus tard.

Les opérateurs linéaires sont également connus comme transformations ou applications linéaires linéaire. Beaucoup d'autres opérateurs une rencontres en mathématiques sont linéaires et opérateurs linéaires sont les plus faciles à étudier (Comparer avec non-linéarité).

Un tel exemple d'une transformation linéaire entre les vecteurs de réflexion R ² est: étant donné un vecteur x = (x _1, x ₂₎

Q (x _1, x ₂₎ = (- x _1, x ₂₎

Nous pouvons aussi donner un sens opérateurs linéaires entre les généralisations de finie espaces de dimension vectorielles. Par exemple, il ya un grand nombre de travaux portant sur les opérateurs linéaires sur Espaces de Hilbert et sur Espaces de Banach. Voir également algèbre de l'opérateur.

Les opérateurs de la théorie des probabilités

Les opérateurs sont également impliqués dans la théorie des probabilités. Ces opérateurs que attente, la variance , covariance, factorielles , etc.

Les opérateurs de calcul

Calcul est, essentiellement, l'étude de deux opérateurs particuliers: la opérateur différentiel D = d / d t, et la opérateur intégrale indéfinie 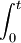. Ces opérateurs sont linéaires, comme le sont la plupart des opérateurs construits d'eux. Dans les régions les plus avancées de mathématiques, ces opérateurs sont étudiées dans le cadre de analyse fonctionnelle.

L'opérateur différentiel

Le opérateur différentiel est un opérateur qui est fondamentalement utilisé dans le calcul pour désigner l'action de prendre un dérivé. Notations sont communes dy / dx, et y '(x) pour indiquer la dérivée de y (x). Ici, cependant, nous allons utiliser la notation qui est plus proche de la notation de l'opérateur que nous utilisons; ce est, en utilisant Df pour représenter l'action de prendre la dérivée de f.

Opérateurs intégraux

Étant donné que l'intégration est un opérateur ainsi (inverse de la différentiation), nous avons quelques opérateurs importants, nous pouvons écrire en termes d'intégration.

Convolution

La convolution est une application de deux fonctions f (t) et g (t) à une autre fonction, définie par une intégrale de la manière suivante:

Transformée de Fourier

La transformée de Fourier est utilisé dans de nombreux domaines, non seulement en mathématiques, mais en physique et en traitement du signal, pour ne en nommer que quelques-uns. Ce est un autre opérateur intégral; il est utile principalement parce qu'il convertit une fonction sur une (spatiale) de domaine d'une fonction à une autre (fréquence) domaine, d'une manière qui est efficace inversible. Rien de significatif est perdu, parce qu'il ya une transformation inverse opérateur. Dans le cas simple de des fonctions périodiques, ce résultat est basé sur le théorème que toute fonction périodique continue peut être représentée comme la somme d'une série de ondes sinusoïdales et des vagues de cosinus:

Lorsque vous traitez avec fonction générale R → C, la transformation prend une intégrante forme:

Laplacien transformer

La transformation de Laplace est un autre opérateur intégré et est impliqué dans la simplification du processus de résolution d'équations différentielles.

Compte tenu de f = f (s), elle est définie par:

Opérateurs fondamentaux sur les champs scalaires et vectoriels

Trois principaux opérateurs sont la clé de calcul vectoriel , l'opérateur ∇, connu sous le nom gradient, où à un certain point dans un champ scalaire forme un vecteur qui pointe dans la direction du plus grand changement de ce champ scalaire. Dans un champ de vecteurs, le divergence est un opérateur qui mesure la tendance d'un champ de vecteurs en provenance ou à converger vers un point donné. Curl, dans un champ de vecteur, est un opérateur vectoriel qui montre la tendance d'un champ de vecteurs à tourner autour d'un point.

Relation de taper la théorie

En la théorie des types, un opérateur lui-même est une fonction, mais a un type joint indiquant le bon opérande, et le type de fonction renvoyée. Les fonctions peuvent donc être considérés comme des opérateurs à l'inverse, pour lequel nous oublions une partie du bagage de type, laissant étiquettes seulement pour le domaine et codomaine.

Opérateurs en physique

Dans la physique , un opérateur prend souvent un sens plus spécialisé que dans les mathématiques. Opérateurs observables sont un élément clé de la théorie de la mécanique quantique . Dans cet opérateur de contexte signifie souvent un une transformation linéaire à partir de Hilbert espace à un autre, ou (plus abstraitement) un élément d'un C * -algèbre.

Opérateurs des langages de programmation informatique

En général, le terme «opérateur» dans l'ordinateur langages de programmation a la même signification que dans les mathématiques. Ceci est particulièrement vrai dans langages de programmation fonctionnelle, où un opérateur est également une fonction.

Opérateurs primitives

Cependant, la plupart des langages de programmation de distinction entre les opérateurs et les fonctions à ce que les opérateurs sont une partie primitive spéciale de la langue, à la fois syntaxiquement et en termes de fonctionnalité. Par exemple, la plupart des langues offrent un ' + "(Plus) l'opérateur, qui ajoute deux nombres sans faire un appel de fonction.

Dans de nombreuses langues, ce comportement est totalement différente de celle d'un appel de fonction. Par exemple, dans C (et de nombreux dérivés tels que Java ), les opérateurs arithmétiques peuvent agir sur tout numérique type de données, tandis que les fonctions ne sont autorisés à agir sur un seul type explicite.

Autres langues (principalement les plus anciens) ne ont pas de fonctions qui retournent des valeurs du tout. Cependant, ils ont souvent encore les opérateurs qui ne renvoyer des valeurs, l'élargissement de la distinction entre les opérateurs et les fonctions.

Les opérateurs non-mathématiques

Les langages de programmation comportent souvent des opérateurs non-mathématiques. Ceux-ci peuvent inclure les exploitants qui font référence ou déréférencer pointeurs, qui accèdent éléments du tableau, ou obtenir le taille d'un type de données. Ils peuvent également comprendre des opérateurs composés tels que « += », qui incrémente une variable d'une valeur donnée.

Opérateurs en langage d'assemblage

En Assemblée programmation de langue, le terme "opérateur" peut se référer à la opcode d'une instruction donnée. Ceci est très similaire au concept d'un opérateur primitif dans un langage de niveau supérieur.