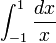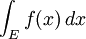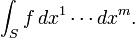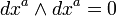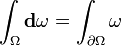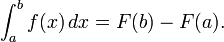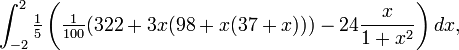Intégrale
Contexte des écoles Wikipédia
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Une bonne façon d'aider d'autres enfants est de parrainer un enfant
- Le mot «intégrale» (adjectif) peut aussi signifier: "étant un entier ".
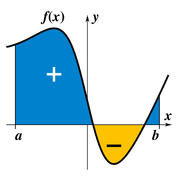
L'intégration est un concept de base du avancées mathématiques , en particulier dans les domaines de calcul et l'analyse mathématique . Etant donné une fonction f (x) d'un véritable et une variable x intervalle [a, b] de la ligne réelle, l'intégrale
est égale à la superficie d'une région dans la Plane xy délimitée par la graphe de f, l'axe des x, et la verticale lignes x = a et x = b, avec des zones ci-dessous l'axe des x étant soustraite.
Le terme «partie intégrante» peut également se référer à la notion de primitive, une fonction F dont la dérivée est la fonction donnée f. Dans ce cas, il est appelé une intégrale indéfinie, tandis que les intégrales abordées dans cet article sont appelés intégrales définies. Certains auteurs soutiennent une distinction entre primitives et intégrales indéfinies.
Les principes d'intégration ont été formulées par Isaac Newton et Gottfried Leibniz à la fin du XVIIe siècle. Par le biais du théorème fondamental du calcul , qui ils ont développé indépendamment, l'intégration est liée à la différenciation, et l'intégrale définie d'une fonction peuvent être facilement calculés fois une primitive est connue. Intégrales et dérivés sont devenus les outils de base de calcul , avec de nombreuses applications de la science et de l'ingénierie.
Une définition mathématique rigoureuse de l'intégrale a été donnée par Bernhard Riemann . Il est basé sur une limitation de procédure qui se rapproche de la surface d'une région curviligne par rupture de la région en brames minces verticaux. Dès le XIXe siècle, les notions plus sophistiquées de intégrante ont commencé à apparaître, où le type de la fonction ainsi que le domaine sur lequel l'intégration est effectuée a été généralisée. Un intégrale curviligne est définie pour les fonctions de deux ou trois variables, et l'intervalle d'intégration [a, b] est remplacé par une certaine courbe reliant deux points sur le plan ou dans l'espace. Dans un intégrale de surface, la courbe est remplacé par un morceau de surface dans l'espace à trois dimensions. Intégrales de formes différentielles jouent un rôle fondamental dans moderne géométrie différentielle . Ces généralisations intégrante premier découlaient des besoins de la physique , et ils jouent un rôle important dans la formulation de nombreuses lois physiques, notamment ceux de électrodynamique. Les concepts modernes de l'intégration sont basés sur la théorie mathématique abstrait connu comme l'intégration de Lebesgue , développé par Henri Lebesgue.
Histoire
L'intégration pré-calcul
L'intégration peut être retracée aussi loin que l'Egypte ancienne, vers 1800 avant JC, avec le Papyrus de Moscou démontrant des connaissances d'une formule pour le volume d'une pyramide tronc. La technique systématique première documentée capable d'intégrales déterminant est le méthode de l'épuisement des Eudoxe (vers 370 avant JC), qui visait à trouver des aires et des volumes en les décomposant en un nombre infini de formes pour lesquelles la zone ou le volume était connu. Cette méthode a été développée et utilisée par Archimède et utilisée pour calculer les zones de paraboles et une approximation de la surface d'un cercle. Des méthodes similaires ont été développés indépendamment en Chine vers le 3e siècle par Liu Hui, qui l'a utilisé pour trouver la zone du cercle. Cette méthode a été utilisé plus tard par Zu Chongzhi pour trouver le volume d'une sphère. Quelques idées de calcul intégral se trouvent dans le Siddhanta Shiromani, un texte de 12 l'astronomie siècle par le mathématicien indien Bhāskara II.
Des avancées significatives sur des techniques telles que la méthode de l'épuisement ne commencent à apparaître jusqu'à ce que le 16ème siècle AD. A ce moment le travail de Cavalieri avec sa méthode des indivisibles, et le travail par Fermat , a commencé à jeter les bases du calcul moderne. D'autres mesures ont été faites au début du 17e siècle par Barrow et Torricelli, qui a fourni les premiers indices d'un lien entre l'intégration et différenciation.
Newton et Leibniz
L'avancée majeure dans l'intégration est venu dans le 17ème siècle avec la découverte indépendante du théorème fondamental du calcul par Newton et Leibniz . Le théorème démontre un lien entre l'intégration et la différenciation. Cette connexion, combinée avec la facilité comparative de différenciation, peut être exploitée pour calculer des intégrales. En particulier, le théorème fondamental du calcul permet de résoudre une classe beaucoup plus large de problèmes. Égaux en importance est le cadre mathématique complète que les deux Newton et Leibniz développés. Étant donné le nom calcul infinitésimal, il a permis pour une analyse précise des fonctions au sein des domaines continus. Ce cadre est finalement devenu moderne Calculus , dont la notation pour les intégrales est tiré directement du travail de Leibniz.
Formaliser intégrales
Alors que Newton et Leibniz ont fourni une approche systématique à l'intégration, leur travail ne avait pas un degré de rigueur. L'évêque Berkeley mémorable attaqué infinitésimales que "les fantômes de quantité Departed". Calcul acquis une base plus solide avec le développement de limites et a reçu une fondation appropriée par Cauchy dans la première moitié du 19ème siècle. Intégration a été rigoureusement formalisé, en utilisant des limites, par Riemann . Bien que tous les morceaux borné fonctions continues sont Riemann intégrable sur un intervalle borné, par la suite des fonctions plus générales ont été considérés, à laquelle la définition de Riemann ne se applique pas, et Lebesgue formulé une définition différente de l'intégrale, fondée en théorie de la mesure. D'autres définitions de intégrante, se étendant des approches de Riemann et Lebesgue'S, ont été proposées.
Notation
Isaac Newton a utilisé une petite barre verticale dessus d'une variable pour indiquer l'intégration, ou placé la variable dans une boîte. La barre verticale a été facilement confondu avec 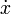 ou
ou 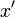 , Que Newton utilisé pour indiquer la différenciation, et la notation de la boîte était difficile pour les imprimantes de reproduire, de sorte que ces notations ne ont pas été largement adopté.
, Que Newton utilisé pour indiquer la différenciation, et la notation de la boîte était difficile pour les imprimantes de reproduire, de sorte que ces notations ne ont pas été largement adopté.
La notation moderne pour l'intégrale indéfinie a été introduit par Gottfried Leibniz en 1675 (Burton, 1988, p 359;. Leibniz 1899, p 154.). Il a adapté le symbole intégrante, "∫", à partir d'un lettre S allongé, debout pour summa (latin pour «somme» ou «total»). La notation moderne de l'intégrale définie, avec des limites ci-dessus et ci-dessous le signe intégrante, a été d'abord utilisé par Joseph Fourier de Mémoires de l'Académie française autour de 1819 à 1820, reproduit dans son livre de 1822 (Cajori 1929, pp 249-250;. Fourier 1822, §231). En Notation mathématique arabe qui se écrit de droite à gauche, un symbole intégrante inversé 22px est utilisé (W3C 2006).
Terminologie et notation
Si une fonction a une intégrale, il est dit être intégrable. La fonction pour laquelle l'intégrale est calculée est appelée l'intégrale. La région sur laquelle une fonction est intégrée est appelée le domaine de l'intégration. Si l'intégrale n'a pas un domaine de l'intégration, il est considéré indéterminée (une avec un domaine est considérée comme définitive). En général, l'intégrale peut être une fonction de plusieurs variables, et le domaine d'intégration peut être une zone, volume, une région de plus grande dimension, ou encore un espace abstrait qui ne possède pas une structure géométrique au sens habituel.
Le cas le plus simple, l'intégrale d'une fonction réelle f d'une variable réelle x sur l'intervalle [a, b], est désigné par
Le signe de ∫, un "S" allongé, représente l'intégration; a et b sont la limite inférieure et la limite supérieure de l'intégration, de définir le domaine de l'intégration; f est la fonction à intégrer, d'être évalué comme x varie sur l'intervalle [a, b ]; dx et peut avoir des interprétations différentes en fonction de la théorie utilisées. Par exemple, il peut être considéré comme une simple notation indiquant que x est la «variable fictive» de l'intégration, comme un reflet des poids dans la somme de Riemann, une mesure (dans l'intégration de Lebesgue et ses extensions), un infinitésimal (en non -standard analyse) ou comme une quantité mathématique indépendante: un forme différentielle. Plus les cas compliqués peuvent varier légèrement la notation.
Introduction
Intégrales apparaissent dans de nombreuses situations pratiques. Envisager une piscine. Si elle est rectangulaire, puis de sa longueur, la largeur, la profondeur et on peut facilement déterminer le volume d'eau qu'il peut contenir (à remplir), la zone de sa surface (pour le couvrir), et la longueur de son bord (à ce câble). Mais se il est de forme ovale avec un fond arrondi, toutes ces quantités se nomment pour les intégrales. Approximations pratiques peuvent suffire au début, mais finalement nous exiger des réponses exactes et rigoureuses à ces problèmes.

Pour commencer, pensez à la courbe y = f (x) entre x = 0 et x = 1, f (x) = √ x. Nous demandons:
- Quel est l'aire sous la fonction f, dans l'intervalle de 0 à 1?
et d'appeler ce domaine (encore inconnue) l'intégrale de f. La notation pour cette intégrale sera
En première approximation, regardez l'unité carré donné par les côtés x = 0 à x = 1 et y = f (0) = 0 et y = f (1) = 1. Sa superficie est exactement 1. Comme il est, la vraie valeur de l'intégrale doit être un peu moins. La diminution de la largeur des rectangles d'approximation donne un meilleur résultat; donc traverser l'intervalle en cinq étapes, en utilisant les points d'approximation 0, 1/5, 2/5, et ainsi de suite à 1. Monter une boîte pour chaque étape en utilisant la hauteur de l'extrémité droite de chaque pièce de la courbe, donc √ 1/5, √ 2/5, et ainsi de suite pour √1 = 1. La somme des aires de ces rectangles, nous obtenons une meilleure approximation de l'intégrale recherchés, à savoir
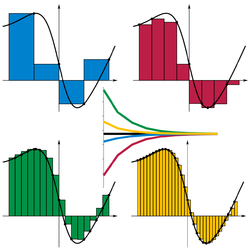
Notez que nous prenons une somme d'un nombre fini de valeurs de la fonction de f, multiplié avec les différences de deux points d'approximation suivantes. Nous pouvons facilement voir que le rapprochement est encore trop grande. Utilisation de plusieurs étapes produit une approximation plus proche, mais ne sera jamais exacte: remplacer les cinq sous-intervalles par douze comme représenté, nous aurons une valeur approximative pour le domaine de 0,6203, ce qui est trop petit. L'idée clé est la transition d'ajouter un nombre fini de différences de points de rapprochement multiplié par leurs valeurs de la fonction respectifs à l'aide infiniment amende, ou étapes infinitésimales.
En ce qui concerne le calcul réel des intégrales, le théorème fondamental du calcul , en raison de Newton et Leibniz, est le lien fondamental entre les opérations de différenciation et d'intégration. Appliqué à la courbe de la racine carrée, f (x) = x 1/2, il est dit de regarder la fonction connexe F (x) = 2/3 x 3/2, et tout simplement prendre F (1) - F (0) , 0 et 1 sont les limites de la intervalle [0,1]. (Ce est un cas d'une règle générale, que pour f (x) = x q, avec q ≠ -1, la fonction connexe, le soi-disant primitive est F (x) = (x 1 q) / (q + 1).) Ainsi, la valeur exacte de l'aire sous la courbe est calculée officiellement comme
La notation
conçoit l'intégrale comme une somme pondérée, désigné par la "S" allongé, avec des valeurs de fonction, f (x), multiplié par largeurs de pas infinitésimales, les soi-disant différences, désignés par dx. Le signe de multiplication est généralement omise.
Historiquement, après l'échec des premiers efforts pour interpréter rigoureusement infinitésimaux, Riemann formellement intégrales définie comme une limite des sommes pondérées, de sorte que le dx suggéré la limite d'une différence (à savoir, la largeur de l'intervalle). Lacunes de la dépendance de Riemann sur les intervalles et la continuité motivé définitions plus récentes, en particulier l' intégrale de Lebesgue , qui est fondée sur une capacité à étendre l'idée de "mesure" de manière beaucoup plus souple. Ainsi, la notation
se réfère à une somme pondérée, dans lequel les valeurs de fonction sont partitionnés, avec μ la mesure du poids à attribuer à chaque valeur. Ici A désigne la région d'intégration.
Géométrie différentielle , avec son "tartre sur collecteurs ", donne encore la notation familière autre interprétation. Maintenant, f (x) dx et devenir forme différentielle, ω = f (x) dx, une nouvelle opérateur différentiel d, connu sous le nom dérivée extérieure apparaît, et le théorème fondamental devient le plus général Théorème de Stokes,
à partir duquel Le théorème de Green, le théorème de la divergence et le théorème fondamental du calcul suivi.
Plus récemment, infinitésimales ont réapparu avec rigueur, grâce à des innovations modernes telles que analyse non-standard. Non seulement ces méthodes revendiquent les intuitions des pionniers, ils conduisent également à de nouvelles mathématiques.
Bien qu'il existe des différences entre ces conceptions de intégrale, il ya un chevauchement considérable. Ainsi, la zone de la surface de la piscine ovale peut être manipulé comme une ellipse géométrique, en tant que somme des infinitésimales, comme une intégrale de Riemann, comme une intégrale de Lebesgue, ou comme un collecteur avec une forme différentielle. Le résultat calculé sera le même pour tous.
Les définitions officielles
Il ya beaucoup de façons de définir formellement une intégrale, dont tous ne sont équivalents. Les différences existent surtout pour faire face aux différentes situations particulières qui peuvent ne pas être intégrable dans d'autres définitions, mais aussi parfois pour des raisons pédagogiques. Les définitions les plus couramment utilisés sont intégrante intégrales de Riemann et intégrales Lebesgue.
Intégrale de Riemann

L'intégrale de Riemann est définie en termes de Sommes de Riemann de fonctions à l'égard de partitions marqués d'un intervalle. Laissez [a, b] être un intervalle fermé de la ligne réelle; puis une partition marqués de [a, b] est une séquence finie
Ce partitionne l'intervalle [a, b] i en sous-intervalles [x i -1, x i], dont chacun est "marqué" avec un point distingué t i ∈ [x i -1, x i]. Soit Δ i = x i - x i -1 être la largeur de sous-intervalle i; puis les mailles d'un tel partage étiqueté est la largeur du plus grand sous-intervalle formé par la cloison, max i = 1 ... n Δ i. Une somme de Riemann d'une fonction f par rapport à une telle partition marquée est définie comme
Ainsi, chaque terme de la somme est l'aire d'un rectangle ayant une hauteur égale à la valeur de la fonction au niveau du point de la sous-intervalle donné distingué, et une largeur identique à la largeur de sous-intervalle. L'intégrale de Riemann d'une fonction f sur l'intervalle [a, b] est égal à S si:
- Pour tous ε> 0, il existe δ> 0 tel que, pour ne importe quelle partition marqués [a, b] avec un maillage inférieur à δ, nous avons
Lorsque les balises choisies donnent le maximum (respectivement minimum) la valeur de chaque intervalle, la somme de Riemann devient supérieure (respectivement inférieure) Darboux somme, suggérant le lien étroit entre l'intégrale de Riemann et Darboux intégrante.
Intégrale de Lebesgue
L'intégrale de Riemann ne est pas défini pour une large gamme de fonctions et de situations d'importance dans les applications (et d'intérêt pour la théorie). Par exemple, l'intégrale de Riemann peut facilement intégrer la densité de trouver la masse d'une poutre d'acier, mais ne peut pas accueillir une bille d'acier reposant sur elle. Cela motive d'autres définitions, en vertu duquel un assortiment plus vaste de fonctions est intégrable (Rudin, 1987). L'intégrale de Lebesgue, en particulier, réalise une grande flexibilité en dirigeant l'attention sur les poids dans la somme pondérée.
La définition de l'intégrale de Lebesgue commence donc par une mesure, μ. Dans le cas le plus simple, le Mesure de Lebesgue μ (A) d'un intervalle A = [a, b] est sa largeur, b - a, de sorte que l'intégrale de Lebesgue accord avec la (bonne) intégrale de Riemann lorsque deux existent. Dans les cas plus complexes, les jeux étant mesurées peuvent être très fragmenté, sans continuité et aucune ressemblance avec des intervalles.
Pour exploiter cette flexibilité, intégrales Lebesgue inverser l'approche de la somme pondérée. Comme Folland (1984, p. 56) le dit, «Pour calculer l'intégrale de Riemann de f, on partitionne le domaine [a, b] en sous-intervalles", tandis que dans l'intégrale de Lebesgue, "une est en vigueur partitionner la gamme de f ».
Une approche commune définit d'abord l'intégrale de la fonction indicatrice d'un mesurables ensemble A par:
 .
.
Ceci prolonge par une linéarité de mesurable fonction simple s, qui atteint seulement un nombre fini, n, des valeurs non-négatives distinctes:
(Où l'image de A i sous la simple fonction s est la valeur constante a i). Ainsi si E est un ensemble mesurable on définit
Alors pour tout non-négative fonction mesurable f définit une
ce est l'intégrale de f est réglée pour être la borne supérieure de toutes les intégrales de fonctions simples qui sont inférieures ou égales à f. Une fonction f mesurable général, est divisé en ses valeurs positives et négatives, en définissant
Enfin, f est Lebesgue intégrable si
et ensuite l'intégrale est définie par
Lorsque l'espace de mesure sur laquelle les fonctions sont définies est aussi un localement compact espace topologique (comme ce est le cas avec le nombres réels R), mesure compatible avec la topologie dans un sens approprié ( Mesures de Radon, dont la mesure de Lebesgue est un exemple) et solidaire à leur égard peut être défini différemment, à partir des intégrales de fonctions continues avec support compact. Plus précisément, les fonctions support compact forment un espace vectoriel qui porte un naturel topologie, et un (Radon) mesure peuvent être définis comme ne importe quelle continue fonctionnelle linéaire sur cet espace; la valeur d'une mesure à une fonction support compact est alors aussi, par définition, l'intégrale de la fonction. On procède ensuite à étendre la mesure (l'intégrale) à des fonctions plus générales par la continuité, et définit la mesure d'un ensemble comme l'intégrale de sa fonction d'indicateur. Ce est l'approche adoptée par Bourbaki (2004) et un certain nombre d'autres auteurs. Pour plus de détails voir Mesures de Radon.
Autres intégrales
Bien que les intégrales de Riemann et Lebesgue les définitions les plus importants de l'intégrale, un certain nombre d'autres existent, notamment:
- Le Intégrale de Stieltjes, une extension de l'intégrale de Riemann.
- Le Lebesgue-Stieltjes intégrante, développé par Johann Radon, qui généralise le Riemann-Stieltjes et Lebesgue intégrales .
- Le Daniell intégrante, qui subsume l' intégrale de Lebesgue et Lebesgue-Stieltjes intégrante sans la dépendance mesures.
- Le Henstock-Kurzweil intégrante, diversement définie par Arnaud Denjoy, Oskar Perron, et (le plus élégamment, comme la jauge intégrante) Jaroslav Kurzweil, et développé par Ralph Henstock.
Propriétés de l'intégration
Linéarité
- La collection de fonctions intégrables Riemann sur un intervalle fermé [a, b] forme un espace vectoriel dans les opérations d'addition et de multiplication ponctuelle par un scalaire, et l'opération d'intégration
- est un linéaire fonctionnel sur cet espace vectoriel. Ainsi, d'une part, l'ensemble des fonctions intégrables est fermé sous prise combinaisons linéaires; et, d'autre part, l'intégrale d'une combinaison linéaire est la combinaison linéaire des intégrales,
- De même, l'ensemble des biens à valeurs fonctions intégrables Lebesgue sur une donnée mesure l'espace E avec mesure μ est fermé sous prenant combinaisons linéaires et donc former un espace vectoriel, et l'intégrale de Lebesgue
- est une fonction linéaire dans cet espace de vecteur, de sorte que
- Plus généralement, pensez à l'espace vectoriel de tous fonctions mesurables sur un espace de mesure (E μ,), prenant des valeurs dans un localement compact complet espace vectoriel topologique V sur une localement compact champ topologique K, f: E → V. Puis on peut définir un plan d'intégration abstraite attribuant à chaque fonction f un élément de V ou le symbole ∞,
- qui est compatible avec les combinaisons linéaires. Dans ce cas, la linéarité est valable pour le sous-espace de fonctions dont l'intégrale est un élément de V (ce est à dire «fini»). Les cas particuliers les plus importants se posent lorsque K représente un groupe R, C, ou une extension finie du champ Q de p nombres p-adiques, et V est un espace vectoriel de dimension finie sur K, et quand K = C et V est un complexe Espace de Hilbert.
Linéarité, avec quelques propriétés de continuité naturelles et la normalisation pour une certaine classe de fonctions "simples", peut être utilisé pour donner une autre définition de l'intégrale. Ce est l'approche de Daniell pour le cas de fonctions réelles sur un ensemble X, généralisée par Nicolas Bourbaki à des fonctions à valeurs dans un espace vectoriel topologique localement compact. Voir (Hildebrandt 1953) pour une caractérisation axiomatique de l'intégrale.
Inégalités pour des intégrales
Un certain nombre d'inégalités générales pour tenir Riemann-intégrables fonctions définies sur un fermé et délimitée intervalle [a, b] et peut être généralisée à d'autres notions de Lebesgue intégrante (et Daniell).
- Limites supérieure et inférieure. Une fonction f intégrable sur [a, b], est nécessairement délimitée sur cet intervalle. Ainsi il ya des nombres réels m et M de sorte que m ≤ f (x) ≤ M pour tout x dans [a, b]. Etant donné que les montants inférieur et supérieur de f sur [a, b] sont donc délimités respectivement par m (b - a) et M (b - a), il se ensuit que
- Les inégalités entre les fonctions. Si f (x) ≤ g (x) pour chaque x dans [a, b], puis chacune des sommes supérieures et inférieures de f est majorée par les sommes supérieures et inférieures, respectivement, de g. Ainsi
- Il se agit d'une généralisation des inégalités ci-dessus, que M (b - a) est l'intégrale de la fonction constante ayant une valeur M sur [a, b].
- Sous-intervalles. Si [c, d] est un sous-intervalle de [a, b] et f (x) est non-négatif pour tous x, puis
- Produits et valeurs absolues des fonctions. Si f et g sont deux fonctions alors nous pouvons considérer leur produits ponctuelles et pouvoirs, et des valeurs absolues :
- Si f est Riemann-intégrable sur [a, b] alors la même chose est vraie pour | f |, et
- De plus, si f et g sont deux Riemann-intégrable alors f 2, g 2, et fg sont également Riemann-intégrable, et
- Cette inégalité, connu sous le nom Inégalité de Cauchy-Schwarz, joue un rôle important dans La théorie de l'espace de Hilbert, où le côté gauche est interprété comme le produit scalaire de deux fonctions de carré intégrable f et g sur l'intervalle [a, b].
- L'inégalité de Hölder. Supposons que p et q sont deux nombres réels, 1 ≤ p, q ≤ ∞ avec 1 / + 1 p / q = 1 et F et G sont deux fonctions Riemann-intégrables. Ensuite, la fonctions | f | p et | g | q sont également intégrable et la suivante L'inégalité de Hölder détient:
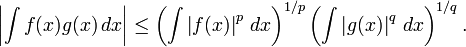
- Pour p = q = 2, l'inégalité de Hölder devient l'inégalité de Cauchy-Schwarz.
- L'inégalité de Minkowski. Supposons que p ≥ 1 est un nombre réel et f et g sont des fonctions de Riemann-intégrables. Puis | f | p, | g | p et | f + g | p sont également Riemann intégrable et la suivante Minkowski inégalité est:

- Un analogue de cette inégalité pour intégrale de Lebesgue est utilisé dans la construction de L espaces p.
Conventions
Dans cette section f est une valeur réelle de Riemann-intégrable fonction . L'intégrale
sur un intervalle [a, b] est définie si a <b. Cela signifie que les montants supérieur et inférieur de la fonction f sont évalués sur une partition a = x 0 ≤ x ≤ 1. . . ≤ x n = b dont les valeurs x i sont en augmentation. Géométriquement, cela signifie que l'intégration a lieu "gauche à droite", l'évaluation de f dans les intervalles [x i, x i 1] où un intervalle avec un indice plus élevé se trouve à droite de l'un avec un indice inférieur. Les valeurs a et b, les points terminaux de la intervalle, qu'on appelle la limites de l'intégration de f. Intégrales peuvent également être définis si un> b:
- Inverser limites de l'intégration. Si a> b puis définissez
Ce, avec a = b, implique:
- Intégrales sur des intervalles de longueur nulle. Si A est un nombre réel puis
La première convention est nécessaire de prendre en considération des intégrales sur sous-intervalles de [a, b]; le second dit que une intégrale prise sur un intervalle dégénérée, ou d'un stade, devrait être de zéro . Une des raisons de la première convention est que l'intégrabilité de f sur un intervalle [a, b] implique que f est intégrable sur ne importe quel sous-intervalle [c, d], mais dans intégrales particulières ont la propriété que:
- Additivité de l'intégration sur les intervalles. Si c est tout élément, [, b a], puis
Avec la première convention de la relation résultant
est alors bien définie pour ne importe quelle permutation cyclique de a, b, et c.
Au lieu de considérer ce qui précède que les conventions, on peut aussi adopter le point de vue que l'intégration est effectuée sur variétés orientées seulement. Si M est une telle variété M de dimension orientée, et M 'est le même collecteur avec une orientation opposée et ω est une m -forme, alors on a (voir ci-dessous pour l'intégration des formes différentielles):
Théorème fondamental du calcul
Le théorème fondamental du calcul est la déclaration que la différenciation et l'intégration sont des opérations inverses: si un fonction continue est d'abord intégrée et différenciée, la fonction d'origine est récupéré. Une conséquence importante, parfois appelé le deuxième théorème fondamental du calcul, permet de calculer des intégrales en utilisant un primitive de la fonction à intégrer.
Des énoncés de théorèmes
- Théorème fondamental du calcul. Soit f une valeur réelle intégrable fonction définie sur un intervalle fermé [a, b]. Si F est défini par x dans [a, b] par
- alors F est continue sur [a, b]. Si f est continue en x dans [a, b], alors F est différentiable en x, et F '(x) = f (x).
- Deuxième théorème fondamental du calcul. Soit f une fonction intégrable à valeurs réelles définie sur un intervalle fermé [a, b]. Si F est une fonction telle que F '(x) = f (x) pour tout x dans [a, b] (ce est-F est une primitive de f), puis
- Corollaire. Si f est une fonction continue sur [a, b], alors f est intégrable sur [a, b], et F, défini par
- est un anti-dérivée de f sur [a, b]. Par ailleurs,
Extensions
Intégrales impropres
Un intégrante "bonne" Riemann assume la fonction à intégrer est définie et finie sur un intervalle fermé et borné, encadrée par les limites de l'intégration. Une intégrale impropre se produit lorsque l'un ou plusieurs de ces conditions ne est pas satisfaite. Dans certains cas, ces intégrales peuvent être définies en tenant compte de la limite d'une séquence appropriée de Riemann intégrales sur des intervalles progressivement plus grands.
Si l'intervalle est de bornes, par exemple à son extrémité supérieure, puis l'intégrale impropre est la limite en tant que point d'extrémité tend vers l'infini.
Si l'intégrale ne est défini ou finie sur un intervalle de demi-ouverte, par exemple (a, b], puis de nouveau une limite peut fournir un résultat fini.
Ce est, l'intégrale impropre est la limite d'intégrales appropriées comme un point final de l'intervalle d'intégration se rapproche soit une indication nombre réel ou ∞ ou -∞. Dans les cas plus complexes, des limites sont nécessaires aux deux extrémités, ou à des points intérieurs.
Considérons, par exemple, la fonction 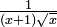 intégré de 0 à ∞ (à droite). À la limite inférieure, comme x passe à 0 la fonction va à ∞, et la limite supérieure est elle-même ∞, si la fonction passe à 0. Ainsi, ce est un doublement intégrale impropre. Intégré, par exemple, 1-3, une somme de Riemann ordinaire suffit pour produire un résultat de
intégré de 0 à ∞ (à droite). À la limite inférieure, comme x passe à 0 la fonction va à ∞, et la limite supérieure est elle-même ∞, si la fonction passe à 0. Ainsi, ce est un doublement intégrale impropre. Intégré, par exemple, 1-3, une somme de Riemann ordinaire suffit pour produire un résultat de  . Pour intégrer de 1 à ∞, une somme de Riemann ne est pas possible. Cependant, toute borne supérieure finie, disent t (avec t> 1), donne un résultat bien défini,
. Pour intégrer de 1 à ∞, une somme de Riemann ne est pas possible. Cependant, toute borne supérieure finie, disent t (avec t> 1), donne un résultat bien défini,  . Cela a une limite finie lorsque t tend vers l'infini, à savoir
. Cela a une limite finie lorsque t tend vers l'infini, à savoir 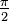 . De même, l'intégrale du tiers-1 permet une somme de Riemann ainsi, par coïncidence produire à nouveau
. De même, l'intégrale du tiers-1 permet une somme de Riemann ainsi, par coïncidence produire à nouveau  . Remplacement tiers par une valeur arbitraire positif s (avec s <1) est tout aussi sûre, donnant
. Remplacement tiers par une valeur arbitraire positif s (avec s <1) est tout aussi sûre, donnant 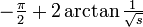 . Cela, aussi, a une limite finie comme s tend vers zéro, à savoir
. Cela, aussi, a une limite finie comme s tend vers zéro, à savoir 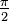 . La combinaison de la limite des deux fragments, le résultat de cette intégrale est incorrecte
. La combinaison de la limite des deux fragments, le résultat de cette intégrale est incorrecte
Ce processus ne est pas garantie de succès; une limite peut échouer d'exister, ou peut être sans limite. Par exemple, sur l'intervalle borné 0-1 l'intégrale de  ne converge pas; et sur l'intervalle bornes 1 à ∞ l'intégrale de
ne converge pas; et sur l'intervalle bornes 1 à ∞ l'intégrale de  ne converge pas.
ne converge pas.
Il peut également arriver que l'intégrande est pas borné à un point intérieur, auquel cas l'intégrale doit être divisé à ce point, et les intégrales limites des deux côtés doit exister et doit être limitée. Ainsi
Mais l'intégrale similaire
ne peut pas être attribué une valeur de cette façon, comme les intégrales au-dessus et au-dessous de zéro faire converger pas de façon autonome. (Toutefois, voir Cauchy valeur principale.)
Intégration multiple
Intégrales peuvent être prises sur des régions autres que les intervalles. En général, une intégrale sur un ensemble E d'une fonction f est écrit:
Voici x ne doit pas être un nombre réel, mais peut être une autre quantité appropriée, par exemple, un vecteur de R 3 . le théorème de Fubini montre que ces intégrales peuvent être réécrites comme une partie intégrante réitéré . En d'autres termes, l'intégrale peut être calculée en intégrant une coordonnée à la fois.
Tout comme l'intégrale définie d'une fonction positive de la variable représente unezonede la région située entre le graphique de la fonction et lexaxe des, ladouble intégraled'une fonction de deux variables positif représente levolume dela région de la surface définie entre par la fonction et le plan qui contient son domaine.(Le même volume peut être obtenu par l'intermédiaire duintégrale triple- l'intégrale d'une fonction à trois variables - de la constante fonctionf(x,y,z) = 1 sur la région mentionnée ci-dessus entre la surface et le plan). Si le nombre de variables est élevé, alors l'intégrale représente unhypervolume, un volume d'un solide de plus de trois dimensions qui ne peuvent pas être représentées graphiquement.
Par exemple, le volume duparallélépipède de côtés 4 x 6 x 5 peut être obtenu de deux façons:
- Par l'intégrale double
- de la fonctionf(x,y) = 5 calculée dans la régionDenxy-Plane qui est la base du parallélépipède.
- Par l'intégrale triple
- de la fonction constante 1 calculé sur le parallélépipède lui-même.
Parce qu'il est impossible de calculer laprimitive d'une fonction de plusieurs variables,indéfinisintégrales multiples existent pas, alors ces intégrales sont tousdéfinitive.
intégrales de ligne
Le concept d'une intégrale peut être étendu à des domaines plus généraux de l'intégration, tels que des lignes et des surfaces courbes. Ces intégrales sont connus comme des intégrales de ligne et intégrales de surface respectivement. Celles-ci ont d'importantes applications en physique, que lorsqu'ils traitent avec des champs de vecteurs.
Une intégrale de ligne (parfois appelée intégrale de chemin ) est une intégrale où la fonction à intégrer est évaluée le long d'une courbe . Diverses différentes intégrales de ligne sont utilisés. Dans le cas d'une courbe fermée, il est aussi appelé une intégrale de contour .
La fonction à être intégrée peut être un champ scalaire ou un champ de vecteurs. , la valeur de l'intégrale de ligne est la somme des valeurs du champ en tout point de la courbe, pondérée par une fonction scalaire sur la courbe (généralement la longueur d'arc ou, pour un vecteur domaine, le produit scalaire du champ de vecteurs avec un vecteur différentiel de la courbe). Cette pondération distingue la ligne intégrante de simples intégrales définies sur des intervalles. Beaucoup de formules simples de la physique ont analogues naturels continus en termes d'intégrales de ligne; par exemple, le fait que le travail est égale à la force multipliée par la distance peut être exprimé (en termes de quantités vectoriels) que:
 ;
;
qui va de pair avec l'intégrale de ligne:
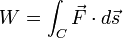 ;
;
qui résume composantes de vecteur le long d'un chemin continu, et donc trouve le travail effectué sur un objet se déplaçant à travers un champ, comme un champ électrique ou gravitationnelle
intégrales de surface
Une intégrale de surface est une intégrale définie pris sur une surface (qui peut être une courbe ensemble dans l'espace); il peut être considéré comme l' analogique intégrale double de l' intégrale de ligne. La fonction à être intégrée peut être un champ scalaire ou un champ de vecteurs. La valeur de l'intégrale de surface est la somme du champ en tout point de la surface. Ceci peut être réalisé en divisant la surface en éléments de surface, qui fournissent la séparation de sommes de Riemann.
Pour un exemple d'applications des intégrales de surface, envisager un champ de vecteurs v sur une surface S ; qui est, pour chaque point x dans S , v ( x ) est un vecteur. Imaginons que nous avons un fluide circulant à travers S , de telle sorte que v ( x ) détermine la vitesse du fluide à x . Le flux est défini comme la quantité de fluide circulant à travers S dans le montant de l'unité de temps. Pour trouver le flux, nous devons prendre le produit scalaire de v avec l'unité de surface normale à S à chaque point, ce qui nous donnera un champ scalaire, que nous intégrons sur la surface:
 .
.
Le flux de fluide dans cet exemple peut être d'un fluide telles que l'eau ou de l'air, ou de flux électrique ou magnétique. Ainsi intégrales de surface ont des applications dans la physique , en particulier avec la théorie classique de l'électromagnétisme .
Intégrales de formes différentielles
Un forme différentielle est un concept mathématique dans les domaines de lafonction de plusieurs variables,la topologie différentielle et tenseurs.La notation moderne pour la forme différentielle, ainsi que l'idée des formes différentielles comme étant lesproduits de coin dedérivés extérieurs formant unealgèbre extérieure, a été présenté par Élie Cartan.
Nous travaillons d'abord dans un ensemble ouvert dans R n . A 0-forme est définie comme une fonction lisse f . Lorsque nous intégrons une fonction f sur une m - dimensions sous-espace S de R n , nous l'écrivons comme
(Les exposants sont des indices, et non des exposants.) On peut considérer dx 1 travers dx n être objets formels eux-mêmes, plutôt que les étiquettes annexées à faire intégrales ressemblent Riemann résume. Alternativement, nous pouvons les considérer comme covecteurs, et donc une mesure de la «densité» (d'où intégrable dans un sens général). Nous appelons le dx 1 , ..., dx n base 1- formes .
Nous définissons leproduit de coin, "∧", bilinéaire "multiplication" opérateur sur ces éléments, avec l'alternancedes biens qui
pour tous les indices a . On notera que l'alternance avec linéarité implique dx b ∧ dx une = - dx une ∧ dx b . Cela garantit également que le résultat du produit en forme de coin a une orientation.
Nous définissons l'ensemble de tous ces produits d'être de base 2- formes , et de même, nous définissons l'ensemble des produits de la forme dx une ∧ dx b ∧ dx c être base 3- formes . Un général k -forme est alors une somme pondérée de base k- formes, où les poids sont des fonctions lisses f . Ensemble, ils forment un espace vectoriel de base avec k -Formulaires que les vecteurs de base, et 0-formes (fonctions lisses) que le champ de scalaires. Le produit de coin se prolonge ensuite à k -Formulaires de façon naturelle. Plus de R n dans la plupart n covecteurs peut être linéairement indépendant, donc un k- forme avec k > n sera toujours zéro, par l'établissement alternatif.
En plus du produit de calage, il existe également le dérivé opérateur extérieur d . Cette carte de l'opérateur k -Formulaires à ( k +1) -Formulaires. Pour un k ω de -forme = f dx une sur R n , on définit l'action de d par:
avec extension au généralk-Formulaires survenant linéairement.
Cette approche plus générale permet une approche plus naturelle de coordonner-libre de l'intégration sur les collecteurs . Il permet également une généralisation naturelle du théorème fondamental du calcul , appelé Théorème de Stokes, que nous pouvons affirmer que
où ω est un général k -form, et ∂Ω désigne la limite de la région Ω. Ainsi, dans le cas où ω est un 0-forme et Ω est un intervalle fermé de la ligne réelle, ce qui réduit le théorème fondamental du calcul . Dans le cas où ω est une forme 1 et Ω est une région en 2 dimensions dans le plan, le théorème réduit à le théorème de Green. De même, en utilisant 2-formes, et 3-formes et dualité de Hodge, nous pouvons arriver à Théorème de Stokes et de la théorème de la divergence. De cette façon, nous pouvons voir que les formes différentielles fournissent une vue unificateur puissant d'intégration.
Les méthodes et applications
intégrales Informatique
La technique la plus base pour calculer des intégrales d'une variable réelle est basée sur le théorème fondamental du calcul . Il procède comme ceci:
- Choisir une fonctionf(x) et un intervalle [a,b].
- Trouver une primitive def, autrement dit, une fonctionFtelle queF '=f.
- Par le théorème fondamental du calcul, à condition que la fonction à intégrer et intégrale ont passingularités sur la voie de l'intégration,
- Par conséquent, la valeur de l'intégrale estF(b) -F(a).
Notez que l'intégrale est pas réellement la primitive, mais le théorème fondamental nous permet d'utiliser des primitives pour évaluer les intégrales définies.
L'étape est souvent difficile de trouver une primitive de f . Il est rarement possible de regard sur une fonction et écrivez sa primitive. Le plus souvent, il est nécessaire d'utiliser l'une des nombreuses techniques qui ont été développées pour évaluer les intégrales. La plupart de ces techniques réécrire une intégrale comme un autre qui est je l'espère plus docile. Les techniques comprennent:
- Intégration par substitution
- Intégration par parties
- Intégration par substitution trigonométrique
- Intégration par fractions partielles
- Intégration par les formules de réduction
Même si ces techniques échouent, il peut toujours être possible d'évaluer une intégrale donnée. La prochaine technique la plus courante est le calcul des résidus, tandis que pour les intégrales non élémentaire série de Taylor peut parfois être utilisé pour trouver la primitive. Il ya aussi beaucoup moins courantes façons de calculer des intégrales définies; par exemple, l'identité de Parseval peut être utilisé pour transformer une intégrale sur une zone rectangulaire en une somme infinie. Parfois, une intégrale peut être évaluée par un tour; pour un exemple de cela, voir intégrante gaussienne.
Calculs de volumes desolides de révolution peuvent normalement être faites avecl'intégration de disque oul'intégration shell.
Les résultats spécifiques qui ont été travaillées par différentes techniques sont recueillies dans laliste des intégrales.
Algorithmes symboliques
Beaucoup de problèmes en mathématiques, la physique et l'ingénierie impliquent l'intégration où une formule explicite pour l'intégrale est souhaitée. Extensif tables d'intégrales ont été compilées et publiées au fil des ans à cet effet. Avec la propagation des ordinateurs , de nombreux professionnels, les éducateurs et les étudiants se sont tournés vers des systèmes de calcul formel qui sont spécifiquement conçus pour effectuer des tâches difficiles ou pénibles, y compris l'intégration. L'intégration symbolique présente un défi particulier dans le développement de ces systèmes.
Une difficulté mathématique majeur dans l'intégration symbolique est que dans de nombreux cas, une formule fermée pour la primitive d'une fonction plutôt regardant innocemment existe tout simplement pas. Par exemple, il est connu que les primitives des fonctions exp ( x 2 ), x X et sin x / x ne peut être exprimé sous la forme fermée impliquant seulement rationnelles et exponentielles fonctions logarithme , trigonométriques et fonctions trigonométriques inverses, et les opérations de multiplication et la composition; en d'autres termes, aucun des trois fonctions données est intégrable dans fonctions élémentaires. la théorie de Galois différentiel fournit des critères généraux qui permettent de déterminer si la primitive d'une fonction élémentaire est élémentaire. Malheureusement, il se trouve que les fonctions avec des expressions fermées de primitives sont l'exception plutôt que la règle. Par conséquent, les systèmes d'algèbre informatisés ont aucun espoir d'être en mesure de trouver une primitive d'une fonction élémentaire construit au hasard. Sur le côté positif, si les «blocs de construction» pour primitives sont fixés à l'avance, il peut être encore possible de décider si la primitive d'une fonction donnée peut être exprimée en utilisant ces blocs et les opérations de multiplication et de la composition, et de trouver le réponse symbolique à chaque fois qu'il existe. Le algorithme Risch, mis en œuvre dans les Mathematica et Érable systèmes de calcul formel, ne vient que pour les fonctions et primitives construites à partir de fonctions rationnelles, radicaux, logarithme, et les fonctions exponentielles.
Certains intégrandes spéciales se produisent assez souvent pour justifier une étude spéciale. En particulier, il peut être utile d'avoir, dans l'ensemble des primitives, les fonctions spéciales de la physique (comme les fonctions de Legendre, la fonction hypergéométrique, la fonction Gamma et ainsi de suite). Extension de l'algorithme Risch-normand de sorte qu'il comprend ces fonctions est possible, mais difficile.
La plupart des humains ne sont pas en mesure d'intégrer ces formules générales, donc dans un sens ordinateurs sont plus habiles à intégrer des formules très compliquées. Très formules complexes sont peu susceptibles d'avoir-forme fermée primitives, alors comment beaucoup d'un avantage fait ce présent est une question philosophique qui est ouvert pour le débat.
Quadrature numérique
Les intégrales rencontrés dans un cours de calcul de base sont délibérément choisis pour la simplicité; ceux trouvés dans des applications réelles ne sont pas toujours très arrangeant. Certains intégrales ne peuvent pas être trouvés exactement, certains nécessitent des fonctions spéciales qui sont eux-mêmes un défi à calculer, et d'autres sont si complexes que trouver la réponse exacte est trop lent. Cela motive l'étude et l'application de méthodes numériques pour les intégrales approchant, qui utilisent aujourd'hui l'arithmétique flottante sur électroniques numériques ordinateurs . Beaucoup d'idées se leva beaucoup plus tôt, pour les calculs à la main; mais la vitesse des ordinateurs à usage général comme l' ENIAC a créé un besoin d'améliorations.
Les objectifs d'intégration numérique sont l'exactitude, la fiabilité, l'efficacité et la généralité. Des méthodes sophistiquées peuvent largement surperformer une méthode naïve par les quatre mesures (Dahlquist & Björck venir; Kahaner, Moler & Nash 1989; Stoer & Bulirsch 2002). Considérons, par exemple, l'intégrale
qui a la réponse exacte 94 / 25 = 3,76. (Dans la pratique ordinaire, la réponse ne sait pas à l'avance, donc une tâche importante - pas exploré ici -. Est de décider quand une approximation est assez bon) Un «livre de calcul" approche divise la plage de l'intégration dans, disons, 16 morceaux égaux, et calcule les valeurs de fonction.
Valeurs de la fonction espacés x -2.00 -1.50 -1.00 -0.50 0,00 0,50 1,00 1,50 2,00 f(x) 2,22800 2,45663 2,67200 2,32475 0,64400 -0,92575 -0,94000 -0,16963 0,83600 x -1.75 -1.25 -0.75 -0.25 0,25 0,75 1,25 1,75 f(x) 2,33041 2,58562 2,62934 1,64019 -0,32444 -1,09159 -0,60387 0,31734
Utilisation de l'extrémité gauche de chaque pièce, la méthode de rectangle résume 16 valeurs et multiplie fonction de la largeur de l'étape, h , ici 0,25, pour obtenir une valeur approximative de 3,94325 pour l'intégrale. La précision est pas impressionnant, mais le calcul utilise formellement morceaux de largeur infinitésimale, donc d'abord cela peut sembler peu préoccupante. En effet, à plusieurs reprises de doubler le nombre d'étapes finit par produire une approximation de 3,76001. Cependant 2 18 pièces sont nécessaires, une grande dépense de calcul pour si peu de précision; et une portée plus grande précision peut forcer étapes si petite que la précision arithmétique devient un obstacle.
Une meilleure approche remplace les sommets horizontales des rectangles avec des sommets inclinés touchant la fonction aux extrémités de chaque pièce. Cette règle de trapèze est presque aussi facile à calculer; il résume l'ensemble des 17 valeurs de la fonction des poids, mais le premier et le dernier par une moitié, et encore multiplie par la largeur de pas. Cela améliore immédiatement le rapprochement à 3,76925, ce qui est nettement plus précis. En outre, seuls 2 10 pièces sont nécessaires pour atteindre 3,76000, sensiblement moins de calculs que la méthode de rectangle pour une précision comparable.
La méthode de Romberg se fonde sur la méthode de trapèze à grand effet. Tout d'abord, les longueurs de pas sont réduites de moitié de manière incrémentielle, ce qui donne des approximations trapézoïdales désignés par T ( h 0 ), T ( h 1 ), et ainsi de suite, où h k1 est la moitié de h k . Pour chaque nouvelle taille de pas, seulement la moitié des nouvelles valeurs de fonction doivent être calculés; les autres portent au-dessus de la taille précédente (comme indiqué dans le tableau ci-dessus). Mais l'idée est vraiment puissant pour interpoler un polynôme à travers les approximations, et d'extrapoler à T (0). Avec cette méthode numériquement exacte réponse ici ne nécessite que quatre pièces (cinq valeurs de fonction)! Le Lagrange de polynôme d'interpolation { h k , T ( h k )} k= 0 ... 2 = {(4.00,6.128), (2.00,4.352), (1.00,3.908)} est 3,76 + 0,148 h 2 , produisant la valeur extrapolée à 3,76 h = 0.
La quadrature de Gauss nécessite souvent nettement moins de travail pour une précision supérieure. Dans cet exemple, il peut calculer les valeurs de fonction à seulement deux x positions, ± 2 / √3 , puis double chaque valeur et la somme pour obtenir la réponse numériquement exacte. L'explication de ce succès spectaculaire réside dans l'analyse des erreurs, et un peu de chance. Un n- point de la méthode de Gauss est exacte pour les polynômes de degré jusqu'à 2 n -1. La fonction dans cet exemple est un polynôme de degré 3, plus un terme qui annule parce que les critères d'évaluation choisis sont symétriques autour de zéro. (Annulation bénéficie également de la méthode de Romberg.)
Déplacement de la plage a laissé un peu, donc l'intégrale est de -2,25 à 1,75, supprime la symétrie. Néanmoins, la méthode de trapèze est plutôt lent, la méthode d'interpolation polynomiale de Romberg est acceptable, et la méthode de Gauss nécessite le moins de travail - si le nombre de points est connu à l'avance. Ainsi, l'interpolation rationnelle peut utiliser les mêmes évaluations trapézoïdales que la méthode Romberg avec plus d'effet.
comparaison méthode du coût de Quadrature Méthode Trapèze Romberg Rationnel Gauss Points 1048577 257 129 36 Rel.Err. -5.3 × 10-13 -6,3 × 10-15 8,8 × 10-15 3,1 × 10-15 Valeur 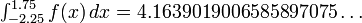
Dans la pratique, chaque méthode doit utiliser les évaluations supplémentaires pour assurer une erreur liée à une fonction inconnue; ce qui tend à compenser une partie de l'avantage de la méthode gaussienne pure, et motive l'hybride populaire Gauss-Kronrod. La symétrie peut encore être exploité en divisant cette intégrale en deux gammes, de -2,25 à -1,75 (pas de symétrie) et de -1,75 à 1,75 (symétrie). Plus largement, quadrature adaptative partitionne une gamme en morceaux basés sur les propriétés de la fonction, de sorte que les points de données sont concentrées là où elles sont le plus nécessaires.
Cette brève introduction omet intégrales de dimensions supérieures (par exemple, la superficie et les calculs de volume), où les alternatives telles quel'intégration de Monte Carlo ont une grande importance.
Un texte de calcul est pas de substitut à l'analyse numérique, mais l'inverse est également vrai. Même le meilleur code numérique adaptative nécessite parfois un utilisateur pour aider avec les intégrales les plus exigeants. Par exemple, intégrales impropres peuvent nécessiter un changement de variable ou méthodes qui peuvent éviter des valeurs de la fonction infinies; et les propriétés connues comme la symétrie et la périodicité peuvent constituer un levier essentiel.
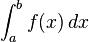
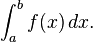
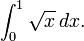

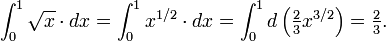

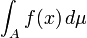
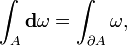


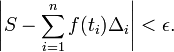
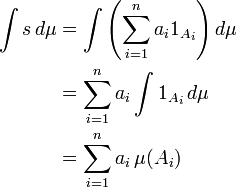
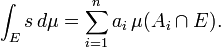


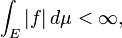
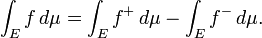
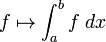
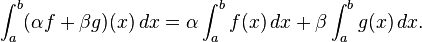
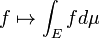
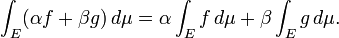
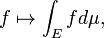
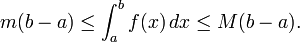
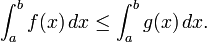

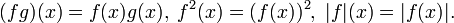
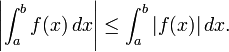
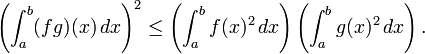


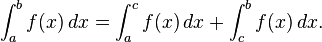
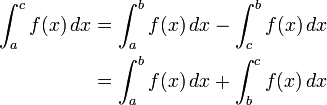
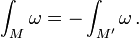

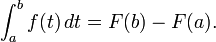


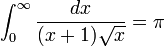
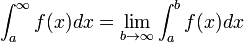
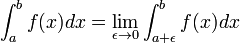
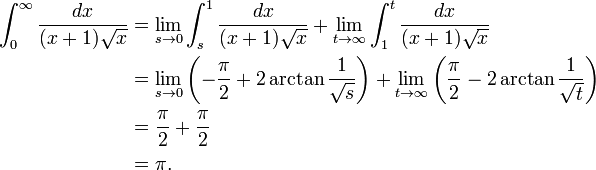
![\ Begin {align} \ int _ {- 1} ^ {1} \ frac {dx} {\ sqrt [3] {x ^ 2}} et {} = \ lim_ {s \ 0} \ int _ {- 1} ^ {- s} \ frac {dx} {\ sqrt [3] {x ^ 2}} + \ lim_ {t \ 0} \ {t} int_ ^ {1} \ frac {dx} {\ sqrt [3 ] {x ^ 2}} \\ & {} = \ lim_ {s \ 0} 3 (1- \ sqrt [3] {s}) + \ lim_ {t \ 0} 3 (1- \ sqrt [ 3] {t}) \\ & {} = 3 + 3 \\ & {} = 6. \ end {align}](../../images/116/11627.png)