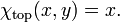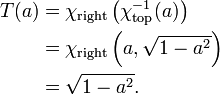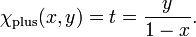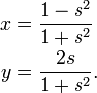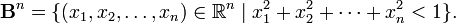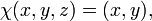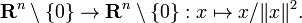Collecteur

Sur une sphère, la somme des angles d'un triangle ne est pas égal à 180 ° (voir trigonométrie sphérique). Une sphère ne est pas un espace euclidien, mais localement les lois de la géométrie euclidienne sont de bonnes approximations. Dans un petit triangle sur la face de la terre, la somme des angles est très près de 180 °. Une sphère peut être représenté par un ensemble de deux cartes dimensions, donc une sphère est un collecteur.

Un collecteur est un résumé espace mathématique dans laquelle chaque point a une quartier qui ressemble à l'espace euclidien , mais dans laquelle la structure globale peut être plus complexe. En discuter collecteurs, l'idée de dimension est importante. Par exemple, les lignes sont à une dimension, et des plans à deux dimensions.

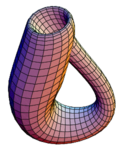
Dans un collecteur unidimensionnelle (ou un collecteur), chaque point a un voisinage qui ressemble à un segment d'une ligne. Des exemples de une-collecteurs comprennent une ligne, un cercle , et deux milieux distincts. Dans un deux-collecteur, chaque point a un voisinage qui ressemble à un disque. Des exemples comprennent un plan, la surface d'une sphère , et la surface d'un tore .

Collecteurs sont des objets importants en mathématiques et en physique , car ils permettent des structures plus complexes pour être exprimées et comprises en termes de propriétés relativement bien compris de simples espaces.

Structures supplémentaires sont souvent définis sur les variétés. Exemples de variétés avec une structure supplémentaire comprennent variétés différentiables sur lequel on peut faire le calcul , Variétés riemanniennes sur lequel distances et les angles peuvent être définis, variétés symplectiques qui servent l'espace de phase dans la mécanique classique , et les quatre dimensions collecteurs de pseudo-riemannienne qui modèle espace-temps de la relativité générale .

Une définition mathématique précise d'un collecteur est donnée ci-dessous. Pour bien comprendre les mathématiques derrière collecteurs, il est nécessaire de connaître les concepts élémentaires concernant ensembles et fonctions , et utile d'avoir une connaissance pratique de calcul et de topologie .

Exemples de motivation

Cercle

Figure 1: Les quatre tableaux chaque carte partie du cercle à un intervalle ouvert, et, ensemble, couvrent tout le cercle.

Le cercle est l'exemple le plus simple d'un collecteur topologique après une ligne. Topologie ignore torsions, un petit morceau d'un cercle est exactement le même que un petit morceau d'une ligne. Considérons, par exemple, la moitié supérieure de la cercle unité, x ² + y ² = 1, où le -Coordonner y est positif (indiqué par l'arc jaune sur la figure 1). Tout point de ce demi-cercle peut être décrit de façon unique par son x -Coordonner. Alors, projection sur la première coordonnée est une continue et inversible , cartographie du demi-cercle supérieur de la intervalle ouvert (-1,1):

Ces fonctions sont appelées tableau s. De même, il existe des cartes pour le fond (rouge), à gauche (bleu) et (vert) bonnes pièces du cercle. Ensemble, ces parties couvrent l'ensemble du cercle et les quatre tableaux font atlas pour le cercle.

Les graphiques haut et droite se chevauchent: leur intersection se trouve dans le quartier du cercle où les deux x - et les -coordinates de y sont positives. Le _sommet de deux cartes de χ et χ _{droite à} chaque carte cette partie dans l'intervalle (0,1). Ainsi, une fonction de T (0,1) pour lui-même peut être construite, qui utilise le premier inverse du diagramme de base pour atteindre le cercle, puis suit le tableau arrière droit de l'intervalle. Soit a un nombre quelconque de (0,1), puis:

Une telle fonction est appelée une carte de transition.

Figure 2: Un cercle tableau collecteur basée sur la pente, couvrant l'ensemble mais un point du cercle.

Le haut, bas, gauche et droite graphiques montrent que le cercle est une variété, mais ils ne font pas les seules possibles atlas. Graphiques ne sont pas nécessairement des projections géométriques, et le nombre de cartes est un sujet de choix. Considérez les cartes

et

Ici s est la pente de la ligne par le point de coordonnées (x, y) et le point de pivot fixe (-1,0); t est l'image en miroir, avec un point de pivot (+1,0). La mise en correspondance inverse de s à (x, y) est donnée par

Il peut facilement être confirmé que x ² + y ² = 1 pour toutes les valeurs de la pente de l'art. Ces deux tableaux fournissent une seconde atlas pour le cercle, avec

Chaque tableau omet un seul point, soit (-1,0) pour s ou (+1,0) pour t, de sorte que ni tableau seul est suffisant pour couvrir l'ensemble du cercle. Topologie peut prouver qu'il ne est pas possible de couvrir le cycle complet avec un seul tableau. Par exemple, même se il est possible de construire un cercle à partir d'un intervalle de ligne unique par le chevauchement et «coller» les extrémités, cela ne produit pas un tableau; une partie du cercle sera associée à deux extrémités à la fois, de perdre inversibilité.

Autres courbes

Quatre collecteurs de courbes algébriques: ■ cercles, ■ parabole, hyperbole ■, ■ cube.

Collecteurs ne doivent pas être connecté (all in "One Piece"); ainsi une paire de cercles distincts est également un collecteur. Ils ne doivent pas être fermée; ainsi un segment de ligne sans ses points d'extrémité est un collecteur. Et ils ne doivent pas être finie; ainsi un parabole est un collecteur. Rassembler ces libertés, deux autres exemples de collecteurs sont un hyperbole (deux pièces, infinies ouvertes) et le lieu des points sur la courbe cubique y ² = x ³ - x (une pièce de boucle fermée et, une pièce infini ouvert).

Cependant, nous excluons des exemples comme deux cercles touchantes qui partagent un point pour former une figure-huit; au point partagé nous ne pouvons pas créer un graphique satisfaisant. Même avec la flexion admis par la topologie, le voisinage du point partagé ressemble à un "+", pas une ligne.

Cercle enrichi

Vu en utilisant le calcul , la fonction transition cercle T est simplement une fonction entre les intervalles ouverts, ce qui donne un sens à la déclaration que T est différentiable . La carte de transition T, et tous les autres, sont différentiables sur (0, 1); donc, avec cet atlas est un cercle variété différentiable. Il est aussi lisse et analytique parce que les fonctions de transition ont ces propriétés ainsi.

Autres propriétés du cercle lui permettent de répondre aux exigences de types plus spécialisés de collecteur. Par exemple, le cercle a une notion de distance entre deux points, la longueur d'arc entre les points; par conséquent, ce est un Variété riemannienne.

Histoire

L'étude des variétés combine de nombreux domaines importants des mathématiques: il généralise concepts tels que courbes et surfaces ainsi que des idées de l'algèbre linéaire et de topologie .

Préhistoire

Avant le concept moderne d'un collecteur, il y avait plusieurs résultats importants.

La géométrie non-euclidienne considère espaces où Euclide l ' postulat des parallèles échoue. Saccheri d'abord les études à 1733. Lobachevsky, Bolyai et Riemann entre eux ont développé 100 ans plus tard. Leur recherche a découvert deux types d'espaces dont les structures géométriques différer de celle de classique espace euclidien ; ceux-ci ont donné lieu à géométrie hyperbolique et géométrie elliptique. Dans la théorie moderne de collecteurs, ces notions correspondent à Variétés riemanniennes avec négative constante et positive courbure, respectivement.

Carl Friedrich Gauss peut avoir été le premier à considérer espaces abstraits comme des objets mathématiques dans leur propre droit. Son theorema egregium donne une méthode de calcul de la courbure d'une surface sans tenir compte du espace ambiant dans lequel se trouve la surface. Une telle surface serait, dans la terminologie moderne, être appelé un collecteur; et en termes modernes, le théorème prouvé que la courbure de la surface est une propriété intrinsèque. Théorie Manifold est venu de se concentrer exclusivement sur ces propriétés intrinsèques (ou invariants), tout en ignorant largement les propriétés extrinsèques de l'espace ambiant.

Un autre, plus topologique exemple d'un intrinsèque la propriété d'un collecteur est sa caractéristique d'Euler . Leonhard Euler a montré que pour une forme convexe polytope dans l'espace euclidien à trois dimensions avec des sommets (V) ou des coins, des bords E, et F faces,

V - E + F = 2.

La même formule tiendra si nous projetons les sommets et les arêtes du polytope sur une sphère , la création d'une «carte» avec des sommets de V, bords de E, et F visages, et en fait, restera vrai pour ne importe quelle carte sphérique, même si elle ne se pose pas de tout polytope convexe. Ainsi, la figure 2 est un invariant topologique de la sphère, appelée sa caractéristique d'Euler. D'autre part, un tore peut être tranché ouverte par sa cercles 'Meridian' «parallèle» et la création d'une carte avec V = 1 vertex, E = deux bords, et F = 1 visage. Ainsi, la caractéristique d'Euler du tore est de 1 à 2 + 1 = 0. La caractéristique d'Euler d'autres surfaces est utile invariant topologique, qui peut être étendue à des dimensions supérieures à l'aide Nombres de Betti. Dans le milieu du XIXe siècle, le Théorème de Gauss-Bonnet liée la caractéristique d'Euler à la courbure gaussienne.

Synthèse

Enquêtes de Niels Henrik Abel et Carl Gustav Jacobi sur inversion de intégrales elliptiques dans la première moitié du 19e siècle les ont amenés à envisager des types particuliers de variétés complexes, maintenant connu comme Jacobiens. Bernhard Riemann a également contribué à leur théorie, la clarification du sens géométrique du processus de prolongement analytique de fonctions de variables complexes, bien que ces idées étaient en avance sur leur temps.

Une autre source importante de collecteurs dans le 19ème siècle était les mathématiques mécanique analytique, tel que développé par Siméon Poisson, Jacobi, et William Rowan Hamilton. Les états possibles d'un système mécanique sont considérés comme des points d'un espace abstrait, espace de phase Lagrange et Formalismes hamiltonien de la mécanique classique. Cet espace est, en fait, une grande dimension-collecteur, dont la dimension correspond aux degrés de liberté du système et où les points sont spécifiés par leur coordonnées généralisées. Pour un mouvement sans contrainte de particules libres le collecteur est équivalent à l'espace euclidien, mais diverses lois de conservation limitent à des formations plus complexes, par exemple Liouville tori. La théorie d'un corps solide en rotation, développé dans le 18ème siècle par Leonhard Euler et Joseph Lagrange , donne un autre exemple où le collecteur ne est pas triviale. Aspects géométriques et topologiques de la mécanique classique ont été soulignés par Henri Poincaré, l'un des fondateurs de la topologie .

Riemann a été le premier à faire un travail considérable de généraliser l'idée d'une surface aux dimensions supérieures. Le nom vient du collecteur d'origine de Riemann allemande terme, Mannigfaltigkeit, qui William Kingdon Clifford traduit comme "multiplicité". Dans sa leçon inaugurale Göttingen, Riemann décrit l'ensemble de toutes les valeurs possibles d'une variable à certaines contraintes comme Mannigfaltigkeit, car la variable peut avoir de nombreuses valeurs. Il distingue stetige Mannigfaltigkeit et Diskrete Mannigfaltigkeit (de multiplicité et multiplicité continue discontinue), selon que les changements de valeur continue ou non. Comme exemples continues, Riemann se réfère à non seulement les couleurs et les emplacements des objets dans l'espace, mais aussi les formes possibles d'une figure spatiale. Utilisation induction, Riemann construit un n-fach ausgedehnte Mannigfaltigkeit (n fois multiplicité prolongé ou multiplicité de dimension n) en tant que pile continue de (n-1) manifoldnesses dimensions. Notion intuitive de Riemann d'un Mannigfaltigkeit évolué dans ce qui est aujourd'hui formalisée comme un collecteur. Variétés riemanniennes et surfaces de Riemann sont nommés d'après Bernhard Riemann.

Hermann Weyl a donné une définition intrinsèque variétés différentiables dans son cours magistral sur les surfaces de Riemann en 1911-1912, ouvrant la voie à la notion générale d'un espace topologique qui a suivi peu de temps. Durant les années 1930 Hassler Whitney et d'autres clarifié la aspects fondamentaux de la personne, et donc intuitions datant de la seconde moitié du 19ème siècle sont devenus précise, et développées à travers la géométrie différentielle et la théorie des groupes de Lie.

Topologie des variétés: faits saillants

Collecteurs en deux dimensions, aussi connu comme surfaces, ont été examinées par Riemann sous le couvert de surfaces de Riemann , et rigoureusement classés dans le début du 20e siècle par Poul Heegaard et Max Dehn. Henri Poincaré pionnier de l'étude des variétés en trois dimensions et a soulevé une question fondamentale à leur sujet, aujourd'hui connu sous le nom Conjecture de Poincaré. Après près d'un siècle d'efforts par de nombreux mathématiciens, en commençant par Poincaré lui-même, un consensus parmi les experts (en 2006), ce est que Grigori Perelman a prouvé la conjecture de Poincaré (voir le Solution de la conjecture de Poincaré Hamilton-Perelman). Bill Thurston programme de géométrisation, formulée dans les années 1970, à condition d'une extension en profondeur de la conjecture de Poincaré aux collecteurs tridimensionnels générales. Quatre dimensions collecteurs ont été portés à l'avant-garde de la recherche mathématique dans les années 1980 par Michael Freedman et dans un contexte différent, par Simon Donaldson, qui a été motivé par les progrès alors récente en physique théorique ( Théorie de Yang-Mills), où ils servent comme un substitut pour ordinaire 'plat' l'espace-temps. Un important travail sur les variétés de dimension supérieure, y compris des analogues de la conjecture de Poincaré, avait été fait plus tôt par René Thom, John Milnor, Stephen Smale et Sergei Novikov. Une des techniques les plus répandues et flexibles sous-jacents beaucoup de travail sur la topologie des variétés est La théorie de Morse.

Définition mathématique

Officieusement, un collecteur est un espace qui est "calqué sur" l'espace euclidien .

Il existe de nombreux types de variétés et des généralisations. En la géométrie et la topologie, tous les collecteurs sont variétés topologiques, éventuellement avec une structure supplémentaire, le plus souvent un la structure différentiable. En termes de construction de collecteurs via patch, un collecteur a une structure supplémentaire si les cartes de transition entre les différents patchs satisfont axiomes au-delà de la continuité. Par exemple, variétés différentiables ont homéomorphismes sur les quartiers se chevauchent difféomorphes uns avec les autres, de sorte que le collecteur a un ensemble bien défini de fonctions qui sont différentiables dans chaque quartier, etc. dérivable sur le collecteur dans son ensemble.

Formellement, un collecteur topologique est un seconde dénombrable Hausdorff espace qui est localement homéomorphe à l'espace euclidien.

Deuxième comptable et sont séparé point set conditions; seconde exclut dénombrables espaces de cardinal supérieur comme le longue lignée, tout séparé exclut espaces tels que "la ligne avec deux origines" (ces collecteurs généralisées sont discutés dans non séparé collecteurs).

Localement homéomorphe à l'espace euclidien signifie que chaque point a un voisinage homéomorphe à un euclidienne ouverte n -boule,

Généralement collecteurs sont prises pour avoir une dimension fixe (l'espace doit être localement homéomorphe à un fixe n -Ball), et un tel espace est appelé un n -manifold; Cependant, certains auteurs admettre collecteurs où différents points peuvent avoir différents dimensions. Depuis dimension est un invariant local, chaque composant connecté a une dimension fixe.

Schéma-théoriquement, un collecteur est un annelé espace localement, dont la structure faisceau est localement isomorphe à la gerbe de continu (ou différentiables, ou analytique complexe, etc.) fonctions sur l'espace euclidien. Cette définition est principalement utilisé lors de la discussion collecteurs analytiques dans géométrie algébrique.

Définition large

La large définition commune de collecteur est un espace topologique localement homéomorphe à un espace vectoriel topologique sur les réels. Ce omet les axiomes de point-set (permettant cardinalités plus élevés et non-Hausdorff collecteurs) et la dimension finie (ce qui permet de divers collecteurs analyse fonctionnelle). Habituellement on se détend un ou l'autre condition: collecteurs sans les axiomes de point-set sont étudiés dans topologie générale, tandis que les variétés de dimension infinie sont étudiés dans analyse fonctionnelle.

Graphiques, atlas et cartes de transition

La Terre sphérique est navigué en utilisant des cartes ou des tableaux plats, recueillies dans un atlas. De même, une variété différentiable peut être décrite à l'aide cartes mathématiques, appelées coordonner les arbres, recueillies dans un atlas mathématiques. Il ne est généralement pas possible de décrire un collecteur avec un seul tableau, parce que la structure globale du collecteur est différente de la structure simple des charts. Par exemple, aucune carte forfaitaire unique peut bien représenter la Terre entière. Quand un collecteur est construit à partir de plusieurs graphiques qui se chevauchent, les régions où ils se chevauchent présentent les informations essentielles à la compréhension de la structure globale.

Hit-parade

Une carte de coordonner, un tableau de coordonnées, ou tout simplement un tableau, d'un collecteur est un inversible la carte entre un sous-ensemble de l'espace collecteur et un simple tel que à la fois la carte et son inverse préservent la structure désirée. Pour un collecteur topologique, l'espace est simple: un certain espace euclidien R ⁿ et l'intérêt se concentre sur la structure topologique. Cette structure est préservée par homéomorphismes , cartes inversibles qui sont continues dans les deux directions.

Dans le cas d'un variété différentiable, un ensemble de graphiques appelé un atlas nous permet de faire le calcul sur les variétés. Les coordonnées polaires , par exemple, forment un tableau pour le plan R ² moins le axe x positif et l'origine. Un autre exemple d'un tableau est le _haut de la carte χ mentionné dans la section ci-dessus, un tableau pour le cercle.

Atlas

La description de la plupart des collecteurs nécessite plus d'un tableau (un seul graphique est suffisante pour que les collecteurs les plus simples). Une collection spécifique de graphiques qui couvre un collecteur est appelé un atlas. Un atlas ne est pas unique que tous les collecteurs peuvent être couverts de multiples façons en utilisant différentes combinaisons de cartes.

L'atlas contenant toutes les cartes possibles compatibles avec un atlas donné se appelle l'atlas maximales. Contrairement à un atlas ordinaires, l'atlas maximales d'une variété donnée est unique. Bien qu'il est utile pour les définitions, ce est un objet très abstrait et non utilisé directement (par exemple, dans les calculs).

cartes de transition

Graphiques dans un atlas peuvent se chevaucher et un point d'une variété unique peuvent être représenté dans plusieurs tableaux. Si deux cartes se chevauchent, des parties de les représenter de la même région du collecteur, comme une carte de l'Europe et une carte de l'Asie peut contenir à la fois Moscou. Compte tenu de deux graphiques qui se chevauchent, une fonction de transition peuvent être définis qui va de une boule ouverte dans R ⁿ pour le collecteur, puis de nouveau à un autre (ou peut-être le même) boule ouverte dans R ^n. La carte résultante, comme la carte T dans l'exemple de cercle au-dessus, est appelé un changement de coordonnées, une transformation de coordonnées, une fonction de transition, ou une carte de transition.

Structure supplémentaires

Un atlas peut également être utilisé pour définir la structure supplémentaire sur le collecteur. La structure est d'abord défini sur chaque carte séparément. Si toutes les cartes de transition sont compatibles avec cette structure, la structure de transferts vers le collecteur.

Ce est le moyen standard variétés différentiables sont définis. Si les fonctions de transition d'un atlas pour une variété topologique préservent la structure différentielle naturel de R ⁿ (autrement dit, si elles sont difféomorphismes), la structure différentielle transferts vers le collecteur et le transforme en une variété différentiable. Variétés complexes sont introduits d'une manière analogue en exigeant que les fonctions de transition d'un atlas sont fonctions holomorphes. Pour variétés symplectiques, les fonctions de transition doivent être symplectomorphismes.

La structure du collecteur dépend de l'atlas, mais parfois différentes atlas peut dire de donner lieu à la même structure. Ces atlas sont appelés compatible.

Ces notions sont faits précis, en général par l'utilisation de pseudogroups.

Construction

Un seul collecteur peut être construit de différentes manières, en soulignant chacun un aspect différent de la tubulure, ce qui conduit à un point de vue légèrement différent.

Hit-parade

Le graphique des cartes de la part de la sphère avec z positif coordonner sur un disque.

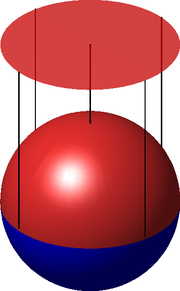
Peut-être le moyen le plus simple pour construire un collecteur est celui utilisé dans l'exemple ci-dessus du cercle. Tout d'abord, un sous-ensemble de R ² est identifié, puis un atlas couvrant ce sous-ensemble est construit. Le concept de collecteur a grandi historiquement de constructions de ce genre. Voici un autre exemple, l'application de cette méthode pour la construction d'une sphère:

Sphère avec des graphiques

Une sphère peut être traitée pratiquement de la même manière que le cercle. En mathématiques une sphère ne est que la surface (et non le solide intérieur), qui peut être définie comme un sous-ensemble de R ^3:

La sphère est en deux dimensions, de sorte que chaque tableau permettra de cartographier partie de la sphère à un sous-ensemble ouvert de R ^2. Envisager l'hémisphère nord, qui est la partie avec z positif coordonnées (couleur rouge sur la photo à droite). La fonction définie par χ

cartes de l'hémisphère nord à l'air libre unité de disque en la projetant sur le plan (x, y). Un tableau similaire existe pour l'hémisphère sud. Avec deux arbres en saillie sur le plan (x, z) et les deux arbres en saillie sur le plan (y, z), un atlas des six arbres est obtenu qui couvre l'ensemble du domaine.

Ceci peut être facilement généralisée aux sphères de dimensions supérieures.

Patchwork

Un collecteur peut être construit en collant ensemble des morceaux d'une manière cohérente, en faire des tableaux qui se chevauchent. Cette construction est possible pour tout collecteur et par conséquent, il est souvent utilisé comme une caractérisation, en particulier pour les variétés différentiables et Riemann. Il se concentre sur un atlas, comme les patchs offrent naturellement graphiques, et puisqu'il n'y a pas d'espace extérieur impliqués elle conduit à une vue intrinsèque de la conduite.

Le collecteur est constitué par la spécification d'un atlas, qui est lui-même défini par des plans de transition. Un point du collecteur est donc un classe d'équivalence de points qui sont mis en correspondance les uns aux autres par des plans de transition. Graphiques carte classes d'équivalence à des points d'un seul patch. Il ya habituellement une forte demande sur la cohérence des cartes de transition. Pour variétés topologiques ils sont tenus d'être homéomorphismes ; se ils sont également difféomorphismes, le collecteur en résulte est une variété différentiable.

Ceci peut être illustré par la carte transition t = ¹ / _s à partir de la seconde moitié de l'exemple de cercle. Commencez avec deux copies de la ligne. Utilisez le S de coordonnées pour la première copie et t pour la deuxième copie. Maintenant, collez les deux copies ensemble par identifiant le point t sur le deuxième exemplaire avec le point ¹ / _s sur la première copie (le point t = 0 ne est pas identifié avec ne importe quel point de la première copie). Cela donne un cercle.

Vue intrinsèque et extrinsèque

La première construction et cette construction sont très semblables, mais ils représentent plutôt différents points de vue. Dans la première construction, le collecteur est considérée comme intégré dans un espace euclidien. Ce est la vue extrinsèque. Quand un collecteur est considéré de cette façon, il est facile à utiliser l'intuition d'espaces euclidiens de définir une structure supplémentaire. Par exemple, dans un espace euclidien il est toujours clair si un vecteur à un moment donné est tangentielle ou normale dans une certaine surface par ce point.

La construction de patchwork ne utilise aucun enrobage, mais considère tout simplement le collecteur comme un espace topologique par lui-même. Ce point de vue abstrait est appelée la vue intrinsèque. Il peut rendre plus difficile à imaginer ce qu'est un vecteur tangent peut être.

n -Sphere comme un patchwork

Le n -sphere S ⁿ est une généralisation de l'idée d'un cercle (une sphère) et la sphère (2-sphère) à des dimensions supérieures. Un -sphere n S ⁿ peut être construit en collant ensemble deux copies de R ^n. La carte de transition entre eux est défini comme

Cette fonction est sa propre inverse et peut donc être utilisé dans les deux sens. Comme le plan de transition est un fonction lisse, cet atlas définit un collecteur lisse. Dans le cas n = 1, simplifie l'exemple à l'exemple donné plus haut de cercle.

Identifier les points d'une variété

Il est possible de définir différents points d'un même collecteur d'être. Ceci peut être visualisé comme ces points de collage en un seul stade, la formation d'une espace quotient. Il est, cependant, pas de raison de se attendre à de tels espaces quotients soient collecteurs. Parmi les espaces possibles de quotient qui ne sont pas nécessairement collecteurs, orbifolds et CW complexes sont considérés comme étant relativement bien comportés.

Un procédé pour identifier des points (les coller ensemble) se fait par une droite (ou gauche) action d'un groupe , qui agit sur le collecteur. Deux points sont identifiés si l'on est déplacé sur l'autre par un élément du groupe. Si M est le collecteur et G est le groupe, l'espace quotient résultant est désigné par M / G (ou G \ M).

Collecteurs qui peuvent être construits en identifiant des points comprennent tori et espaces projectifs réels (à partir avec un plan et une sphère, respectivement).

Produits cartésiens

Le Produit cartésien des collecteurs est également un collecteur. Non chaque collecteur peut être écrit comme un produit d'autres collecteurs.

La dimension de la tubulure de produit est la somme des dimensions de ses facteurs. Sa topologie est la topologie produit, et un produit cartésien de graphiques est un organigramme pour le collecteur de produit. Ainsi, un atlas pour le collecteur de produit peut être construit en utilisant des atlas pour ses facteurs. Si ces atlas définissent une structure différentielle sur les facteurs, les atlas correspondant définit une structure différentielle sur le collecteur de produit. Le même est vrai pour toute autre structure définie sur les éléments. Si l'un des facteurs a une limite, le collecteur de produit a également une limite. Produits cartésiens peuvent être utilisés pour construire tori et finie des cylindres, par exemple, en tant que S ¹ x S ¹ et S ¹ × [0, 1], respectivement.

Un cylindre fini est une variété à bord.

Variété à bord

Une variété à bord est un collecteur avec un bord. Par exemple, une feuille de papier avec des coins arrondis est un 2-variété avec une limite de dimension 1. Le bord d'une -manifold n est un (n-1) -manifold. Un disque (cercle, plus intérieur) est une 2-variété à bord. Sa limite est un cercle, un une-collecteur . Un bille (sphère, plus intérieur) est une 3-variété à bord. Sa limite est une sphère, une 2-variété. (Voir aussi Boundary (topologie)).

En langage technique, une variété à bord est un espace contenant les deux points intérieurs et points limites. Chaque point intérieur a un voisinage homéomorphe au n -boule ouverte {(x _1, x _2, ..., x _n) | Σ x _i ² <1}. Chaque point limite a un voisinage homéomorphe à la "moitié" n -boule {(x _1, x _2, ..., x _n) | Σ x _i ² <1 et ₁ x ≥ 0}. Le homéomorphisme doit envoyer le point limite jusqu'à un point avec x ₁ = 0.

Collage le long des frontières

Deux collecteurs avec des limites peuvent être collés ensemble le long d'une frontière. Si cela est fait de la bonne façon, le résultat est également un collecteur. De même, deux limites d'un seul collecteur peuvent être collées ensemble.

Formellement, le collage est défini par une bijection entre les deux limites. Deux points sont identifiés quand ils sont mis en correspondance sur l'autre. Pour une variété topologique bijection ce doit être un homéomorphisme, sinon, le résultat ne sera pas un collecteur topologique. De même, pour une variété différentiable il doit être un difféomorphisme. Pour les autres collecteurs autres structures devraient être préservés.

Un cylindre fini peut être réalisé sous forme de collecteur en partant d'une bande [0, 1] x [0, 1] et collage d'une paire de bords opposés sur la limite par un difféomorphisme approprié. Un plan projectif peut être obtenu par collage d'une sphère avec un trou à un Möbius bande le long de leurs frontières respectives circulaires.

Classes de collecteurs

Variétés topologiques

Le type le plus simple de variété à définir est le collecteur topologique, qui ressemble localement comme un "ordinaire" espace euclidien R ^n. Formellement, un collecteur topologique est un espace topologique localement homéomorphe à un espace euclidien. Cela signifie que chaque point a un voisinage pour lesquels il existe un homéomorphisme (un bijective fonction continue dont l'inverse est également continu) la cartographie de ce quartier à R ^n. Ces homéomorphismes sont les graphiques du collecteur.

Il est à noter que un collecteur topologique ressemble localement comme un espace euclidien d'une manière plutôt faible: alors que pour chaque tableau individuel, il est possible de distinguer les fonctions différentiables ou mesurer des distances et des angles, du seul fait d'être un collecteur topologique un espace fait pas un choix particulier et cohérente de ces concepts. Afin de discuter de ces propriétés pour un distributeur, il faut préciser davantage la structure et envisager variétés différentiables et variétés riemanniennes ci-dessous. En particulier, un même collecteur topologique sous-jacent peut avoir plusieurs classes mutuellement incompatibles de fonctions différentiables et un nombre infini de façons de spécifier les distances et les angles.

Habituellement hypothèses techniques supplémentaires sur l'espace topologique sont faites pour exclure les cas pathologiques. Il est de coutume d'exiger que l'espace soit Séparé et seconde dénombrable.

La dimension de la variété à un certain point est la dimension de l'espace euclidien que les cartes à ce point carte pour (nombre n dans la définition). Tous les points dans un variété connexe ont la même dimension. Certains auteurs exigent que toutes les cartes d'une carte de collecteur topologique euclidienne des espaces de même dimension. Dans ce cas, toute variété topologique a un invariant topologique, sa dimension. D'autres auteurs permettent syndicats disjoints de variétés topologiques avec différentes dimensions d'être appelés collecteurs.

Variétés différentiables

Pour la plupart des applications, une aimables spécial de variété topologique, une variété différentiable, est utilisé. Si les cartes locales sur un collecteur sont compatibles dans un certain sens, on peut définir les directions, espaces tangents, et fonctions différentiables sur ce collecteur. En particulier, il est possible d'utiliser le calcul sur une variété différentiable. Chaque point d'une variété différentiable de dimension n a une espace tangente. Ce est un espace euclidien de dimension n constitué de la vecteurs tangents des courbes passant par le point.

Deux classes importantes de variétés différentiables sont des variétés lisses et analytiques. Pour les variétés lisses cartes de transition sont lisse, ce est infiniment différentiable. Collecteurs analytiques sont des variétés lisses avec la condition supplémentaire que les cartes de transition sont analytique (ils peuvent être exprimés sous forme de séries de puissance, qui sont essentiellement des polynômes de degré infini). La sphère peut être donnée la structure analytique, tout comme les courbes et les surfaces les plus familiers.

Un ensemble rectifiable généralise l'idée d'un morceaux lisse ou courbe rectifiable à des dimensions supérieures; Toutefois, ensembles rectifiables ne sont pas en collecteurs généraux.

Variétés riemanniennes

Pour mesurer les distances et les angles sur les variétés, le collecteur doit être de Riemann. Une variété riemannienne est une variété différentiable dans lequel chaque espace tangent est équipé d'un produit scalaire <⋅, ⋅> d'une manière qui varie en douceur de point à point. Étant donné deux vecteurs tangents U et V, le produit scalaire <u, v> donne un nombre réel. Le dot (ou scalaire) produit est un exemple typique d'un produit interne. Cela permet de définir diverses notions telles que longueur, les angles , les zones (ou volumes ), courbure, gradients de fonctions et de divergence champs de vecteurs.

Toutes les variétés différentiables (de dimension constante) peuvent être donnés la structure d'une variété riemannienne. L'espace euclidien lui-même une structure naturelle de variété riemannienne (les espaces tangents sont naturellement identifiés avec l'espace euclidien lui-même et portent le produit scalaire niveau de l'espace).Beaucoup de courbes et de surfaces familiers, y compris par exemple lesn-Sphères, sont spécifiés comme des sous-espaces d'un espace euclidien et héritent d'une métrique de leur incorporation en elle.

Collecteurs Finsler

Un collecteur Finsler permet la définition de la distance, mais pas de l'angle; il est un collecteur d'analyse dans lequel chaque espace tangent est équipé d'une norme, || || ·, d'une manière qui varie en douceur de point à point. Cette norme peut être étendue à une métrique définissant la longueur d'une courbe; mais il ne peut pas en général être utilisé pour définir un produit scalaire.

Toute variété riemannienne est un collecteur Finsler.

groupes de Lie

groupes de Lie, nommé d'aprèsSophus Lie, sont des variétés différentiables qui portent également la structure d'ungroupequi est telle que les opérations de groupe sont définis par les cartes lisses.

Un espace vectoriel euclidien avec l'opération de groupe de plus de vecteur est un exemple d'un groupe de Lie non-compact. Un exemple simple d'un compact groupe de Lie est le cercle: l'opération de groupe est tout simplement la rotation. Ce groupe, connu sous le nom U (1), peut également être caractérisé en tant que groupe de nombres complexes de module avec une multiplication en tant que l'opération de groupe. D'autres exemples de groupes de Lie comprennent des groupes spéciaux de matrices , qui sont tous les sous-groupes du groupe linéaire général, le groupe de n par n matrices non nulle déterminant. Si les entrées de la matrice sont des nombres réels , ce sera un n ² -dimensionnelle collecteur déconnecté. Le groupes orthogonaux, les groupes de symétrie de la sphère et hypersphères, sont n ( n -1) / 2, où les variétés de dimension n -1 est la dimension de la sphère. D'autres exemples peuvent être trouvés dans la table des groupes de Lie.

D'autres types de collecteurs

• Un variété complexe est un collecteur sur le modèle C ⁿ avec fonctions de transition holomorphes sur tableau chevauchements. Ces collecteurs sont les objets de base de l'étude de la géométrie complexe. Un collecteur d'un complexe de dimension est appelée une surface de Riemann . Notez qu'un n variété complexe de dimension 2 est de dimension n comme une véritable variété différentiable.
• Un CR collecteurest un collecteur calqué sur les frontières de domaines dansC ⁿ.
• Collecteurs de dimension infinie: pour permettre dimensions infinies, on peut considérercollecteurs de Banach qui sont localement homéomorphe à Espaces de Banach.même, collecteurs Fréchet sont localement homéomorphe à Espaces de Fréchet.
• Un variété symplectique est une sorte de collecteur qui est utilisé pour représenter les espaces de phase dans la mécanique classique . Ils sont doués d'une 2-forme qui définit le crochet de Poisson. Un type étroitement lié de collecteur est un collecteur de contact.

Classification et invariants

Différentes notions de collecteurs ont différentes notions de classification et invariant; dans cette section, nous nous concentrons sur les variétés lisses fermées.

La classification des variétés fermées lisses est bien compris , en principe , sauf en dimension 4: dans les dimensions faibles (2 et 3), il est géométrique, via le théorème de l'uniformisation et de la solution de Hamilton-Perelman de la conjecture de Poincaré, et en haute dimension ( et 5 ci-dessus), il est algébrique, via la théorie de la chirurgie. Ceci est une classification en principe: la question générale de savoir si deux variétés lisses sont difféomorphes est pas calculable en général. En outre, les calculs spécifiques restent difficiles, et il ya de nombreuses questions ouvertes.

Surfaces orientables peuvent être visualisés, et leurs classes de difféomorphisme énumérés, par genre. Compte tenu de deux surfaces orientables, on peut déterminer si elles sont difféomorphes en calculant leurs genres respectifs et en comparant: ils sont difféomorphes si et seulement si les genres sont égaux, de sorte que le genre constitue un ensemble complet d'invariants.

Cela est beaucoup plus difficile dans les dimensions plus élevées: les variétés de dimension plus élevés ne peuvent être directement visualisés (bien que l'intuition visuelle est utile dans les comprendre), ni leurs classes de difféomorphisme peut être énuméré, ni peut-on en général de déterminer si deux descriptions différentes d'une variété de dimensions supérieures reportez-vous au même objet.

Toutefois, on peut déterminer si deux collecteurs sont différents si il ya une caractéristique intrinsèque qui les différencie. Ces critères sont communément appelées invariants , parce que, même si elles peuvent être définies en termes d'une certaine présentation (tels que le genre en termes de triangulation), ce sont les mêmes par rapport à toutes les descriptions possibles d'un collecteur particulier: ils sont invariant sous différentes descriptions.

Naïvement, on pourrait espérer développer un arsenal de critères invariants qui définitivement classer tous les collecteurs à isomorphisme. Malheureusement, il est connu que pour les variétés de dimension 4 et plus, aucun programme existe qui peut décider si deux collecteurs sont difféomorphes.

Variétés lisses ontun riche ensemble d'invariants, venant detopologie point-set, classique topologie algébrique, et topologie géométrique.Les invariants les plus familiers, qui sont visibles pour les surfaces, sontorientability (un invariant normal, aussi détecté parhomologie) etgenre (un invariant homologique).

Lisse collecteurs fermés n'a pas invariants locaux (dimension) autres que, bien que les collecteurs ont invariants géométriques locales, notamment la courbure d'une variété de Riemann et la torsion d'un collecteur équipé d'une connexion affine. Cette distinction entre aucun invariants locales et les invariants locaux est une façon courante de faire la distinction entre la géométrie et la topologie. Tous les invariants d'une variété fermée lisse sont donc mondiale.

Topologie algébrique est une source d'un certain nombre de propriétés invariantes mondiaux importants. Certains critères clés comprennent le simplement connexe propriété et orientability (voir ci-dessous). En effet, plusieurs branches des mathématiques, comme homologie et homotopie théorie et la théorie des classes caractéristiques ont été fondées afin d'étudier les propriétés invariantes des collecteurs.

Des exemples de surfaces

Orientability

En deux dimensions et supérieur, un critère invariant simple mais importante est la question de savoir si un collecteur admet une orientation significative. Considérons une variété topologique avec des graphiques à la cartographie R ⁿ . Compte tenu d'une base commandé pour R ⁿ , un tableau fait sa part du collecteur de se acquérir un sens de l'ordre, qui en 3 dimensions peut être considérée soit comme droitier ou gaucher. Graphiques se chevauchent ne sont pas tenus d'accepter dans leur sens de la commande, ce qui donne une liberté importante collecteurs. Pour certaines variétés, comme la sphère, diagrammes peuvent être choisis de sorte que les régions se chevauchent d'accord sur leur "impartialité"; ceux-ci sont orientables collecteurs. Pour d'autres, cela est impossible. Cette dernière possibilité est facile d'oublier, parce que toute surface fermée intégré (sans auto-intersection) dans l'espace en trois dimensions est orientable.

Quelques exemples de collecteurs non orientables comprennent: (1) leruban de Möbius, qui est une variété à bord, (2) labouteille de Klein, qui doit se coupent en 3-espace, et (3) leplan projectif réel, qui se pose naturellement dansla géométrie.

Ruban de Möbius

Ruban de Möbius

Commencez avec un cylindre circulaire infinie debout verticalement, un collecteur sans limite. Slice travers elle haut et bas pour produire deux limites circulaires, et la bande cylindrique entre eux. Ceci est une variété orientable avec limite, sur laquelle "chirurgie" sera exécutée. Couper la bande ouverte, afin qu'il puisse se dérouler à devenir un rectangle, mais garder une emprise sur les extrémités coupées. Twist un bout à 180 °, ce qui rend le visage de surface intérieure sur, et coller les extrémités de retour ensemble de façon transparente. Il en résulte une bande avec une demi-torsion permanente: l' Ruban de Möbius. Sa limite est plus une paire de cercles, mais (topologiquement) un seul cercle; et ce qui était autrefois son "à l'intérieur" a fusionné avec son «dehors», de sorte qu'il a maintenant qu'un seul côté.

La bouteille de Klein

La bouteille de Klein immergé dans un espace tridimensionnel.

Prenez deux bandes de Möbius; chacun a une seule boucle comme une frontière. Redresser les boucles dans les cercles, et de laisser les bandes faussent en cross-caps. Le collage des cercles ensemble va produire une nouvelle variété fermée sans limite, la bouteille de Klein . Fermeture de la surface ne fait rien pour améliorer le manque de orientability, il supprime simplement la frontière. Ainsi, la bouteille de Klein est une surface fermée sans distinction entre intérieur et extérieur. Notez que dans l'espace en trois dimensions, la surface d'une bouteille de Klein doit passer par lui-même. Construire une bouteille de Klein, qui ne sont pas auto-intersection nécessite quatre ou plusieurs dimensions de l'espace.

Plan projectif réel

Commencez par une sphère centrée sur l'origine. Chaque ligne par l'origine perce la sphère en deux points opposés appelés antipodes . Bien qu'il n'y ait aucun moyen de le faire physiquement, il est possible de fusionner mathématiquement chaque paire de antipode en un seul point. La surface fermée ainsi produit est le plan projectif réel, encore une autre surface non-orientable. Il a un certain nombre de descriptions et constructions équivalentes, mais cette route explique son nom: tous les points sur une ligne donnée par le projet de l'origine à la même "point" sur ce "plan".

Genre et la caractéristique d'Euler

Pour deux variétés de dimension une propriété invariante clé est le genre, ou le «nombre de poignées» présents dans une surface. Un tore est une sphère avec une poignée, un double tore est une sphère avec deux poignées, et ainsi de suite. En effet, il est possible de caractériser complètement les variétés compactes, en deux dimensions sur la base du genre et de orientability. Dans collecteurs de dimensions supérieures genre est remplacé par la notion de caractéristique d'Euler .

Généralisations de collecteurs

• Orbifolds : Un orbifold est une généralisation du collecteur permettant pour certains types de « singularités »dans la topologie. Grosso modo, il est un espace qui ressemble localement comme les quotients de certains simple espace ( par exemple de l'espace euclidien ) par les actions de divers groupes finis. Les singularités correspondent à des points fixes des actions de groupe, et les actions doivent être compatibles dans un certain sens.

• Variétés et des systèmes algébriques : variétés algébriques non-singuliers sur les nombres réels ou complexes sont des variétés. On généralise cette première en permettant singularités, d'autre part en permettant aux différents domaines, et, troisièmement, en émulant la construction de correction de variétés: tout comme un collecteur est collé ensemble à partir de sous-ensemble ouvert de l'espace euclidien, une variété algébrique est collée à partir de variétés algébriques affines, qui ya zéro ensembles de polynômes sur des corps algébriquement clos. schémas sont également collées ensemble des régimes affines, qui sont une généralisation des variétés algébriques. Les deux sont liées à des collecteurs, mais sont construits algébrique utilisant gerbes à la place de atlas.

À cause de points singuliers, une variété est en général pas un collecteur, bien que linguistiquement les FrançaisVariété, allemandMannigfaltigkeitet en anglaiscollecteursont en grande partie synonymes.en français une variété algébrique est appeléjuin Variété algébrique(unevariété algébrique), tandis qu'une variété lisse est appeléejuin Variété différentielle(unevariété différentielle).

• CW-complexes : Un complexe CW est un espace topologique formé par collage des disques de dimension différente ensemble. En général, l'espace qui en résulte est singulier, et par conséquent pas un collecteur. Cependant, ils sont d'un intérêt central dans la topologie algébrique, en particulier dans théorie de l'homotopie , car ils sont faciles à calculer avec singularités et ne sont pas une préoccupation.