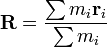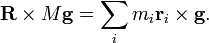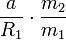Centre de la masse

Saviez-vous ...

Enfants SOS offrent un chargement complet de la sélection pour les écoles pour une utilisation sur les intranets des écoles. Les enfants SOS est le plus grand organisme de bienfaisance du monde en donnant des enfants orphelins et abandonnés la chance de la vie familiale.

En physique , le centre de masse d'un système de particules est un point spécifique qui, pour de nombreuses raisons, le système de la masse se comporte comme si elle était concentrée. Le centre de masse ne est fonction que des positions et des masses des particules qui constituent le système. Dans le cas d'un corps rigide, la position de son centre de masse est fixe par rapport à l'objet (mais pas nécessairement en contact avec elle). Dans le cas d'une distribution des masses en vrac l'espace libre, tel que, par exemple, tiré à partir d'un fusil de chasse, la position du centre de masse est un point l'espace entre eux qui peuvent ne pas correspondre à la position de toute masse individuelle. Dans le contexte d'un champ gravitationnel entièrement uniforme, le centre de masse est souvent appelé le centre de gravité - le point où la gravité peut dire d'agir.

Le centre de masse d'un corps ne coïncide pas toujours avec son centre géométrique intuitive, et l'on peut exploiter cette liberté. Ingénieurs essaient de concevoir un centre de la voiture de sport de gravité aussi bas que possible pour rendre la voiture mieux gérer. Quand sauteurs en hauteur effectuer une " Fosbury Flop ", ils plier leur corps dans une telle manière qu'il est possible pour le cavalier pour effacer la barre alors que son centre de masse ne est pas.

La dite centre de cadre de gravité (un terme moins préférée pour le centre du cadre de l'élan) est un référentiel inertiel défini comme le référentiel inertiel dans lequel le centre de masse d'un système est au repos.

Définition

Le centre de masse $\ Mathbf {R}$ d'un système de particules est définie comme la moyenne de leurs positions $\ Mathbf {r} _i$ , pondérée par leurs masses $m_i$ :

$\ Mathbf {R} = {\ sum m_i \ mathbf {r} _i \ over \ sum m_i}$

Pour un distribution continue avec une densité de masse 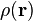$\ Rho (\ mathbf {r})$ et la masse totale $M$ , La somme devient une intégrale:

$\ Mathbf R = \ frac 1M \ int \ mathbf {r} \; dm = \ frac 1M \ int \ rho (\ mathbf {r}) \, \ mathbf {r} \ dV = \ frac {\ int \ rho (\ mathbf {r}) \, \ mathbf {r} \ dV} {\ int \ rho (\ mathbf {r}) \ dV}$

Si un objet a uniforme densité puis son centre de masse est la même que la centre de gravité de sa forme.

Exemples

Le centre de masse d'un système à deux particules se trouve sur la ligne reliant les particules (ou, plus précisément, leurs centres individuels de masse). Le centre de gravité est plus proche de l'objet plus massif; pour plus de détails, voir barycentre ci-dessous.
Le centre de masse d'un anneau est au centre de l'anneau (dans l'air).
Le centre de gravité d'un triangle solide se trouve sur tous les trois médianes et donc au centre de gravité, qui est aussi la moyenne des trois sommets.
Le centre de masse d'un rectangle est situé à l'intersection des deux diagonales.
Dans un corps à symétrie sphérique, le centre de gravité se trouve au centre. Cela se applique à peu près à la Terre : la densité varie considérablement, mais il dépend principalement de profondeur et moins sur les deux autres coordonnées.
Plus généralement, pour toute symétrie d'un corps, son centre de masse sera un point de cette symétrie fixe.

Histoire

Le concept du centre de gravité a été introduit par le grec ancien mathématicien, physicien et ingénieur d'Archimède de Syracuse . Archimède a montré que le couple exercé sur un levier par des poids reposant à différents points le long du levier est le même que ce que ce serait si tous les poids ont été transférés à un seul point - leur centre de gravité. Dans le travail sur les corps flottants il a démontré que l'orientation d'un objet flottant est celui qui fait son centre de gravité aussi bas que possible. Il a développé des techniques mathématiques pour trouver les centres de gravité des objets de densité uniforme de diverses formes bien définies, notamment un triangle, un hémisphère, et un tronc d'un paraboloïde circulaire.

Dans le Moyen Age , les théories sur le centre de gravité ont été développées par Al-Biruni, al-Razi ( latinisé comme Rhazes), Omar Khayyam, et al-Khazini.

Mouvement

Les équations du mouvement suivants supposent l'existence d'un système de particules régies par les forces internes et externes. Une force est une force interne provoqué par l'interaction des particules à l'intérieur du système. Une force externe est une force qui provient de l'extérieur du système, et agit sur une ou plusieurs particules à l'intérieur du système. La force externe ne doit pas être due à un champ uniforme.

Pour ne importe quel système sans forces extérieures, le centre de masse se déplace à vitesse constante. Ceci se applique à tous les systèmes classiques avec des forces internes, y compris les champs magnétiques, les champs électriques, réactions chimiques, et ainsi de suite. Plus formellement, ce est vrai pour toutes les forces internes qui répondent à la forme faible de la troisième loi de Newton .

La quantité de mouvement totale pour tout système de particules est donnée par

$\ Mathbf {p} = M \ mathbf {v} _ \ mathrm {} cm$

Où M indique la masse totale, et v _cm est la vitesse du centre de masse. Cette vitesse peut être calculée en prenant la dérivée temporelle de la position du centre de masse.

Un analogue de la célèbre deuxième loi de Newton est

$\ Mathbf {F} = M \ mathbf {a} _ \ mathrm {} cm$

Où F indique la somme de toutes les forces extérieures sur le système, et un _cm indique l'accélération du centre de masse.

Rotation et centres de gravité

Schéma d'un jouet éducatif qui équilibre sur un point: le CM (C) se installe en dessous de son support (P). Tout objet dont la CM est en dessous de la point d'appui ne sera pas tomber.

Le centre de masse est souvent appelé le centre de gravité, car tout uniforme Champ de gravitation g agit sur un système comme si la masse M du système ont été concentrés au centre de masse R. Cela se voit dans au moins deux manières:

Le l'énergie potentielle gravitationnelle d'un système est égale à l'énergie potentielle d'une particule de point ayant la même masse M situé à R.
Le gravitationnelle couple sur un système est égal au couple M d'une force agissant à R g:
$\ Mathbf {R} \ times M \ mathbf {g} = \ sum_im_i \ mathbf {r} _i \ times \ mathbf {g}.$

Si le champ de gravitation agissant sur un corps ne est pas uniforme, le centre de masse ne présente pas nécessairement ces propriétés pratiques concernant la gravité. Comme la situation est mise en Feynman manuel influent de l ' Cours de physique de Feynman:

"Le centre de masse est parfois appelé le centre de gravité, pour la raison que, dans de nombreux cas, la gravité peut être considérée comme uniforme. ... Dans le cas où l'objet est si grand que le nonparallelism des forces gravitationnelles est significatif, alors la centre où il faut appliquer la force d'équilibrage ne est pas simple à décrire, et il se écarte légèrement de la centre de masse. Ce est pourquoi il faut distinguer entre le centre de masse et le centre de gravité. "

Les auteurs postérieurs sont souvent moins prudent, déclarant que lorsque la gravité ne est pas uniforme, «le centre de gravité" se écarte de la CM. Cet usage semble impliquer un «centre de gravité» bien définie concept pour les champs non uniformes, mais il n'y a pas une telle chose. Même lors de l'examen les forces de marée sur les planètes , il suffit d'utiliser les centres de masse pour trouver le mouvement d'ensemble. Dans la pratique, pour les champs non uniformes, on ne parle tout simplement pas d'un "centre de gravité".

Cadre CM

Le moment cinétique pour un système vecteur est égale à la vitesse angulaire de toutes les particules à travers le centre de masse, ainsi que le moment angulaire du centre de masse, comme se il se agissait d'une seule particule de masse $M$ :

$\ Mathbf {L} _ \ mathrm {} = sys \ mathbf {L} _ \ mathrm {} cm + \ mathbf {L} _ \ mathrm {autour \, cm}$

Ceci est un corollaire de la Parallel Axis Théorème.

Ingénierie

Importance aéronautique

Le centre de masse est un point important sur un avion , ce qui affecte de manière significative la stabilité de l'avion. Pour assurer que l'aéronef est sûr de voler, il est essentiel que le centre de gravité chute dans les limites spécifiées. Cette gamme varie par des avions, mais en règle générale il est centré autour d'un point quart de la distance entre le bord de l'aile d'attaque au bord de fuite de l'aile (le point de corde de trimestre). Si le centre de masse est en avance sur la limite avant, l'avion sera moins maniable, peut-être au point d'être incapable de tourner pendant le décollage ou l'arrondi à l'atterrissage. Si le centre de masse se trouve derrière la limite arrière, le bras du moment de la ascenseur est réduite, ce qui rend plus difficile la récupération à partir d'un décrochage. L'avion sera plus maniable, mais aussi moins stable, et peut-être tellement instable qu'il est impossible de voler.

Barycentre en astronomie

Le barycentre (ou barycentre; du grec βαρύκεντρον) est le point entre deux objets où ils se équilibrent. En d'autres termes, le centre de gravité où deux ou plusieurs corps célestes orbite autour de l'autre. Lorsqu'un lune orbite autour d'une planète , ou une planète orbite autour d'une étoile , les deux organismes sont effectivement en orbite autour d'un point qui se trouve en dehors du centre de la plus grande corps. Par exemple, la lune ne tourne pas le centre exact de la terre, à la place en orbite autour d'un point à l'extérieur du centre de la terre (mais bien en dessous de la surface de la Terre) où leurs masses respectives se équilibrent. Le barycentre est l'un des foyers de la orbite elliptique de chaque corps. Ce est un concept important dans les domaines de l'astronomie , l'astrophysique , etc. (voir problème à deux corps).

Dans un cas simple de deux corps, r _1, la distance entre le centre du premier corps au barycentre est donnée par:

$r_1 = a \ cdot {m_2 \ over m_1 + m_2} = {a \ over 1 + m_1 / m_2}$

où:

a est la distance entre les centres des deux organes;

M ₁ et M ₂ sont les masses des deux corps.

R ₁ est essentiellement le demi-grand axe de l'orbite de la premier corps autour du barycentre - et r ₂ = a - R ₁ du demi-grand axe de l'orbite de la deuxième corps. Lorsque le barycentre est situé dans le corps plus massif, qui apparaît à corps "wobble" plutôt que de suivre une orbite discernable.

Le tableau suivant présente quelques exemples de notre système solaire . Les chiffres sont donnés arrondi à trois chiffres significatifs. Les deux dernières colonnes indiquent R _1, le rayon de la première (plus massifs) corps, et R ₁ / R _1, le rapport de la distance par rapport au barycentre et ce rayon: une valeur inférieure à une montre que le barycentre se trouve à l'intérieur du premier corps.

**Exemples**
Agrandir corps	₁ m (M _E = 1)	Smaller corps	m ₂ (M _E = 1)	une ( km)	r ₁ (Km)	R ₁ (Km)	R ₁ / R ₁
Remarques
Terre	1	Lune	0,0123	384000	4670	6380	0,732
La Terre a un "wobble" perceptible.
Pluton	0,0021	Charon	0.000,254 (0,121 m _Pluton)	19600	2110	1150	1,83
Les deux organismes ont des orbites distinctes autour du barycentre, et en tant que tels Pluton et Charon ont été considérés comme un planète double par beaucoup avant la redéfinition de la planète en Août., 2006
Soleil	333000	Terre	1	150000000 (1 UA)	449	696000	0.000,646
L'oscillation du Soleil est à peine perceptible.
Soleil	333000	Jupiter	318	778000000 (5,20 UA)	742000	696000	1,07
Le Soleil tourne autour d'une barycentre juste au-dessus de sa surface.

Si m ₁ m ₂ >> - ce qui est vrai pour le Soleil et toutes les planètes - alors le rapport r ₁ / R ₁ se rapproche de:

${A \ over R_1} \ cdot {m_2 \ over m_1}$

Par conséquent, le barycentre du système Soleil-planète se trouver en dehors du Soleil que si:

${A \ over R _ {\ bigodot}} \ cdot {{m_ planète} \ over m _ {\ bigodot}}> 1 \; \ Flèche Droite \; {A m_ \ cdot {de}} planète> {R _ {\ bigodot} \ cdot m _ {\ bigodot}} \ environ 2,3 \ times 10 ^ {11} \; m_ {Terre} \; \ Mbox {} km \ environ 1530 \; m_ {Terre} \; \ Mbox {} UA$

Ce est, où la planète est lourd et loin du Soleil

Si Jupiter avait Mercury l 'orbite (57.900.000 km, 0,387 UA), le barycentre Soleil-Jupiter serait seulement 5500 km du centre du Soleil (R ₁ / R ₁ ~ 0,08). Mais même si la Terre avait Eris l'orbite (68 UA), le barycentre Terre-Soleil serait encore dans le Sun (un peu plus de 30000 km du centre).

Pour calculer le mouvement réel du Soleil, vous auriez besoin de la somme de toutes les influences de toutes les planètes , comètes , astéroïdes , etc., du système solaire (voir Problème à N corps). Si toutes les planètes étaient alignées sur le même côté du Soleil, le centre de la masse combinée serait mentir environ 500.000 km de la surface du Soleil.

Les calculs ci-dessus sont basés sur la distance moyenne entre les organes et produisent la valeur r moyenne _1. Mais toutes les orbites sont elliptiques célestes, et la distance entre les corps varie entre le ábsides, en fonction de la excentricité, e. Par conséquent, la position du barycentre varie trop, et il est possible dans certains systèmes pour le barycentre d'être parfois à l'intérieur et parfois l'extérieur du corps plus massif. Cela se produit lorsque:

${1 \ over {1-e}}> {r_1 \ over R_1}> {1 \ over {1 + e}}$

Notez que le système Soleil-Jupiter, avec e = 0,0484 _Jupiter, échoue juste pour se qualifier: 1,05 ≯ 1,07> 0,954.

Animations

Les images sont représentatives, pas simulés.

Deux corps en orbite autour d'une masse semblable barycentre commun. (Similaire à la 90 Antiope système)	Deux corps avec une différence de masse en orbite autour d'un barycentre commun, comme dans le Pluto - Système Charon.	Deux corps avec une différence majeure dans la masse en orbite autour d'un barycentre commun (semblable à la Terre - Lune système)	Deux corps avec une extrême différence de masse en orbite autour d'un barycentre commun (similaires à la Sun - Terre système)
Deux corps avec orbite autour d'une masse semblable barycentre commun avec orbites elliptiques (situation courante pour les étoiles binaires )

Localisation du centre de masse de forme physique 2D arbitraire

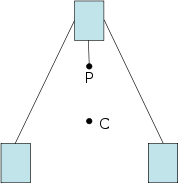
Cette méthode est utile lorsque l'on veut trouver le centre de gravité d'un objet plan complexe avec des dimensions inconnues.


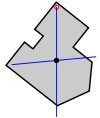Étape 1: Une forme 2D arbitraire.	Étape 2: Suspendre la forme d'un emplacement près d'un bord. Déposez un fil à plomb et la marque sur l'objet.	Étape 3: Suspendre la forme d'un autre endroit pas trop près de la première. Déposez un fil à plomb et marquer. L'intersection des deux lignes est le centre de gravité.

Centre de masse Localisation

Ce est une méthode de détermination du centre de masse d'un objet en forme de L.

CG de l'objet en forme de L-

Divisez la forme en deux rectangles, comme le montre la figure 2. Trouver le centre des masses de ces deux rectangles en tirant les diagonales. Tracez une ligne joignant le centre des masses. Le centre de gravité de la forme doit se trouver sur cette ligne AB.
Divisez la forme en deux autres rectangles, comme le montre la figure 3. Trouver le centre des masses de ces deux rectangles en tirant les diagonales. Tracez une ligne joignant le centre des masses. Le centre de masse de la forme en L doit se trouver sur cette ligne CD.
Comme le centre de masse de la forme doit se situer le long AB et également le long de CD, il est évident que ce est à l'intersection de ces deux lignes, à O. Le point O peut pas mentir intérieur de l'objet en forme de L.

Localisation du centre de masse d'une forme composite

Cette méthode est utile lorsque vous souhaitez trouver le centre de gravité d'un objet qui est facilement divisé en formes primaires, dont les centres de masse sont faciles à trouver (voir Liste des centres de gravité). Nous ne allons trouver le centre de masse dans la direction x ici. La même procédure peut être suivie pour localiser le centre de masse dans la direction y.

COG 1.svg La forme. Il est facilement divisé en un carré, triangle et cercle. Notez que le cercle aura zone négative.

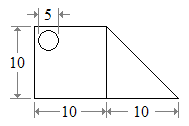COG 2.png Du Liste des centres de gravité, on note les coordonnées des centres de gravité individuels.

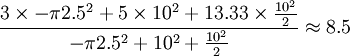COG 3.png D'après l'équation 1 ci-dessus: $\ frac {\ 3 fois - \ pi2.5 ^ 2 + 5 \ times 10 ^ 2 + 13,33 \ times \ frac {10 ^ 2} {2} {} - \ pi2.5 ^ 2 + 10 ^ 2 + \ frac {10 ^ 2} {2}} \ environ 8,5$ unités.

Le centre de masse de ce chiffre est à une distance de 8,5 unités à partir du coin gauche de la figure.

Localisation du centre de masse en traçant autour du périmètre de la forme

Un développement direct de la Planimètre connu comme un Integraph ou integerometer, peut être utilisé pour établir la position du centre de masse de forme irrégulière. Un meilleur terme est probablement instant planimètre. Cette méthode peut être appliquée à une forme avec une limite irrégulière, lisse ou complexe où d'autres méthodes sont trop difficiles. Il a été régulièrement utilisé par les constructeurs de navires pour assurer le navire ne serait pas chavirer. Voir Localisation du centre de masse par des moyens mécaniques.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Center_of_mass&oldid=206108460 "

Privacy Policy and Contacts (IT)