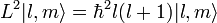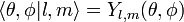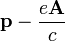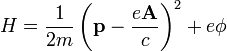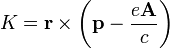Moment angulaire
Renseignements généraux
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| La mécanique classique |
|---|
|
Branches
|
Formulations Mécanique analytique ( Équations de Lagrange Mécanique hamiltonienne) |
Concepts fondamentaux
|
Les sujets fondamentaux Corps rigide
La loi de Newton de gravitation universelle
Inertiel / Non-inertielle cadre de référence
Mécanique des planaire mouvement des particules
|
Un mouvement de rotation Mouvement circulaire
Force centrifuge
|

En physique , le moment cinétique d'une particule sur l'origine est une grandeur vectorielle égale à la masse de la particule multipliée par le produit vectoriel du vecteur de position de la particule avec son vecteur vitesse. Le moment angulaire d'un système de particules est la somme de celle des particules en son sein.
Le moment cinétique est un concept important à la fois dans la physique et de l'ingénierie, de nombreuses applications. Le moment cinétique est importante en physique car ce est un quantité conservée: moment angulaire d'un système reste constante à moins qu'une externe couple agit sur elle. Une symétrie de rotation de l'espace est liée à la conservation du moment cinétique, par exemple, de Théorème de Noether. La conservation du moment angulaire explique beaucoup de phénomènes de la nature.
Moment angulaire en mécanique classique
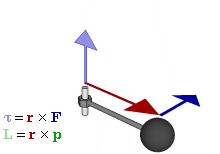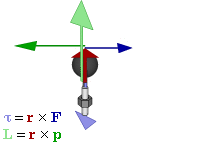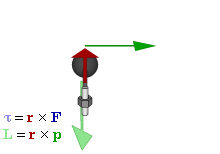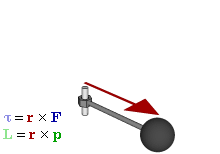
Définition
Le moment cinétique d'une particule sur une origine donnée est défini comme:
où:
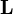 est le moment cinétique de la particule,
est le moment cinétique de la particule, 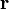 est le vecteur de position de la particule par rapport à l'origine,
est le vecteur de position de la particule par rapport à l'origine, 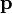 est la quantité de mouvement de la particule, et
est la quantité de mouvement de la particule, et 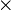 est le vecteur produit de croix .
est le vecteur produit de croix .
Comme on le voit à partir de la définition, la unités SI dérivées de moment angulaire sont newton mètre seconde (N · m · s ou kg · m 2 s -1). En raison du produit vectoriel, L est un pseudovector perpendiculaire à la fois le vecteur r radiale et le vecteur de mouvement p et il est attribué un signe par le Règle de la main droite.
Le moment cinétique d'un ensemble de particules
Si un système est constitué de plusieurs particules, le moment cinétique total sur l'origine peut être obtenue en ajoutant (ou d'intégration) tous les moments cinétiques des particules constitutives. Moment angulaire peut aussi être calculée en multipliant le carré du déplacement r, la masse de la particule et de la vitesse angulaire .
Moment angulaire dans le centre de masse
Il est très souvent commode de considérer le moment cinétique d'une collection de particules au sujet de leur centre de gravité , étant donné que cela simplifie considérablement les mathématiques. Le moment cinétique d'un ensemble de particules est la somme de la quantité de mouvement angulaire de chaque particule:
où  est la distance de la particule i du point de référence,
est la distance de la particule i du point de référence,  est sa masse, et
est sa masse, et  est sa vitesse. Le centre de gravité est défini par:
est sa vitesse. Le centre de gravité est défini par:
où la masse totale de toutes les particules est donnée par
Il se ensuit que la vitesse du centre de masse est
Si nous définissons  que le déplacement de la particule i du centre de masse, et
que le déplacement de la particule i du centre de masse, et 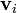 que la vitesse de la particule i par rapport au centre de masse, puis nous avons
que la vitesse de la particule i par rapport au centre de masse, puis nous avons
 et
et 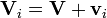
et aussi
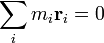 et
et 
de sorte que le moment cinétique total est
Le premier terme est que le moment angulaire du centre de masse. Ce est le même mouvement angulaire l'on obtiendrait se il y avait juste une particule de masse M se déplaçant à la vitesse V située au centre de la masse. Le deuxième terme est la vitesse angulaire qui est le résultat des particules qui se déplacent par rapport à leur centre de masse. Ce second terme peut être encore simplifié si les particules forment une corps rigide, auquel cas un rotation apparaît. Un résultat analogue est obtenu pour une distribution continue de la matière.
Axe de rotation fixe
Pour de nombreuses applications où l'on est seulement préoccupé par rotation autour d'un axe, il suffit de jeter la nature pseudovector du moment angulaire, et de le traiter comme un scalaire où il est positif quand il correspond à un compteur-horaire des rotations, et dans le sens négatif. Pour ce faire, il suffit de prendre la définition du produit croix et jeter le vecteur d'unité, de sorte que le moment angulaire devient:
où θ r, p est l'angle entre r et r p, mesurée à partir de p; une distinction importante parce que sans elle, le signe de la croix produit serait vide de sens. De ce qui précède, il est possible de reformuler la définition d'une des opérations suivantes:
où 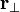 est appelé le distance de bras levier pour p.
est appelé le distance de bras levier pour p.
La meilleure façon de conceptualiser ce est de considérer la distance de bras de levier à la distance de l'origine à la ligne qui se déplace le long p. Avec cette définition, il est nécessaire de tenir compte de la direction de p (sens horaire pointue ou anti-horaire) pour déterminer le signe de L. équivalente:
où  est la composante de p qui est perpendiculaire à r. Comme ci-dessus, le signe est décidé sur la base du sens de rotation.
est la composante de p qui est perpendiculaire à r. Comme ci-dessus, le signe est décidé sur la base du sens de rotation.
Pour un objet avec une masse fixe qui tourne autour d'un axe de symétrie fixe, le moment angulaire est exprimé par le produit de la moment d'inertie de l'objet et son vecteur vitesse angulaire:
où
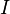 est le moment d'inertie de l'objet (en général, un quantité de tenseur)
est le moment d'inertie de l'objet (en général, un quantité de tenseur)  est la vitesse angulaire .
est la vitesse angulaire .
Comme l' énergie cinétique K d'un corps rotatif massif est donnée par
elle est proportionnelle au carré de la vitesse angulaire.
Conservation du moment cinétique
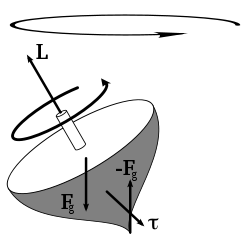
Dans un système fermé moment angulaire est constante. Cette loi de conservation suit mathématiquement de la symétrie directionnelle continue de l'espace (pas de direction dans l'espace est différente de toute autre direction). Voir Théorème de Noether.
La dérivée dans le temps du moment angulaire est appelé couple:
Donc exigeant que le système soit "fermé" ici est mathématiquement équivalente à zéro couple agissant externe sur le système:
où 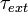 est tout couple appliqué au système de particules.
est tout couple appliqué au système de particules.
En orbite, le moment angulaire est réparti entre la rotation de la planète elle-même et le moment cinétique de son orbite:
 ;
;
Si une planète se trouve à tourner plus lentement que prévu, alors les astronomes soupçonnent que la planète est accompagné par un satellite, parce que le moment cinétique total est partagé entre la planète et son satellite afin d'être conservé.
La conservation du moment angulaire est largement utilisé dans l'analyse de ce qu'on appelle le mouvement de force centrale. Si la force nette sur un corps est dirigée toujours vers un point fixe, le centre, alors il n'y a pas de couple sur le corps par rapport au centre, et de sorte que le moment angulaire du corps autour du centre est constante. Moment angulaire constante est extrêmement utile lorsqu'il se agit de la orbites des planètes et satellites, ainsi que l'analyse de la Modèle de Bohr de l' atome .
La conservation du moment angulaire explique l'accélération angulaire d'un patineur sur glace comme elle apporte ses bras et ses jambes à proximité de l'axe de rotation vertical. En apportant une partie de la masse de son corps près de l'axe, elle diminue le moment d'inertie de son corps. Parce que le moment angulaire est constante en l'absence de couples extérieurs, la vitesse angulaire (vitesse de rotation) du patineur doit augmenter.
Les mêmes résultats phénomène de rotation extrêmement rapide des étoiles compactes (comme les naines blanches , étoiles à neutrons et les trous noirs ) quand ils sont formés sur beaucoup plus grandes et plus lents rotatifs étoiles (en effet, la diminution de la taille de l'objet 10 4 fois des résultats sur l'augmentation de sa vitesse angulaire par le facteur 10 8).
La conservation du moment angulaire dans les résultats de système Terre-Lune dans le transfert de moment angulaire de la Terre à la Lune (en raison de couple de marée la Lune exerce sur la Terre). Cette entraîne à son tour le ralentissement du taux de la Terre de rotation (à environ 42 ns / jour), et augmentation progressive du rayon de l'orbite de la Lune (à ~ 4,5 cm / taux de l'année).
Moment angulaire en mécanique relativiste
Dans moderne (fin du 20e siècle) la physique théorique, le moment angulaire est décrit en utilisant un formalisme différent. Sous ce formalisme, le moment angulaire est le 2-forme Responsable Noether associé à invariance par rotation (En conséquence, le moment angulaire ne est pas conservé pour espaces-temps courbes générales, à moins qu'il ne arrive à être asymptotiquement invariant par rotation). Pour un système de particules ponctuelles sans moment cinétique intrinsèque, il se avère être
(Ici, le produit de coin est utilisé.).
Le moment cinétique en mécanique quantique
En mécanique quantique , le moment angulaire est quantifiée - autrement dit, il ne peut pas varier de façon continue, mais seulement dans " pas de géant "entre certaines valeurs autorisées. Le moment cinétique d'une particule subatomique, en raison de son mouvement à travers l'espace, est toujours un multiple entier de 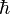 ("H-bar," connu sous le nom Constante de Dirac), définie comme La constante de Planck divisée par 2π. En outre, les expériences montrent que la plupart des particules subatomiques ont, une dynamique permanente intégré angulaire, qui ne est pas en raison de leur mouvement à travers l'espace. Cette moment angulaire de spin vient en unités de
("H-bar," connu sous le nom Constante de Dirac), définie comme La constante de Planck divisée par 2π. En outre, les expériences montrent que la plupart des particules subatomiques ont, une dynamique permanente intégré angulaire, qui ne est pas en raison de leur mouvement à travers l'espace. Cette moment angulaire de spin vient en unités de  . Par exemple, un électron debout au repos a un moment angulaire
. Par exemple, un électron debout au repos a un moment angulaire  .
.
Définition de base
La définition classique de moment cinétique  dépend de six chiffres:
dépend de six chiffres: 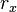 ,
, 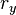 ,
,  ,
,  ,
, 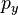 Et
Et 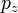 . Traduire cela en termes de mécanique quantique, le Principe d'incertitude de Heisenberg nous dit que ce ne est pas possible pour chacun de ces six numéros à mesurer simultanément avec une précision arbitraire. Par conséquent, il ya des limites à ce qui peut être connu ou mesuré autour de moment cinétique d'une particule. Il se avère que le meilleur que l'on peut faire est de mesurer simultanément l'ampleur de vecteur de moment cinétique et sa composante le long d'un axe.
. Traduire cela en termes de mécanique quantique, le Principe d'incertitude de Heisenberg nous dit que ce ne est pas possible pour chacun de ces six numéros à mesurer simultanément avec une précision arbitraire. Par conséquent, il ya des limites à ce qui peut être connu ou mesuré autour de moment cinétique d'une particule. Il se avère que le meilleur que l'on peut faire est de mesurer simultanément l'ampleur de vecteur de moment cinétique et sa composante le long d'un axe.
Mathématiquement, le moment angulaire en mécanique quantique est défini comme dynamique - non pas comme une quantité, mais comme un opérateur sur la fonction d'onde:
où r et p sont les opérateurs position et impulsion respectivement. En particulier, pour une seule particule sans charge électrique et aucune essorage, le Moment cinétique peut être écrit dans la base de position
où  est l'opérateur vecteur différentiel " Del "(également appelé" Nabla "). Cet opérateur de moment angulaire orbital est la forme la plus couramment rencontré de l'opérateur de moment angulaire, mais pas le seul. Il répond à la suivante canoniques relations de commutation:
est l'opérateur vecteur différentiel " Del "(également appelé" Nabla "). Cet opérateur de moment angulaire orbital est la forme la plus couramment rencontré de l'opérateur de moment angulaire, mais pas le seul. Il répond à la suivante canoniques relations de commutation:
![[L_l, L_m] = i \ hbar \ sum_ {n = 1} ^ 3 \ varepsilon_ {} lmn L_n](../../images/635/63558.png) ,
,
où ε est la lmn (antisymétrique) Symbole de Levi-Civita. De là découle
Depuis,
il se ensuit, par exemple,
Ajout de moments angulaires quantifié
Compte tenu d'un moment cinétique total quantifié 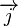 qui est la somme de deux moments cinétiques quantifiés individuelle
qui est la somme de deux moments cinétiques quantifiés individuelle  et
et 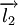 ,
,
la nombre quantique 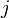 associée à son amplitude peut aller de
associée à son amplitude peut aller de  à
à  par pas entiers dont
par pas entiers dont 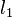 et
et 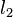 sont des nombres quantiques correspondant aux amplitudes des moments cinétiques individu.
sont des nombres quantiques correspondant aux amplitudes des moments cinétiques individu.
Moment angulaire en tant que générateur de rotations
Si  est l'angle autour d'un axe spécifique, par exemple l'angle azimutal autour de l'axe z, alors la quantité de mouvement angulaire le long de cet axe est le Générateur de rotations autour de cet axe:
est l'angle autour d'un axe spécifique, par exemple l'angle azimutal autour de l'axe z, alors la quantité de mouvement angulaire le long de cet axe est le Générateur de rotations autour de cet axe:
Le fonctions propres de L z sont donc  Et depuis
Et depuis  a une période de
a une période de  , L m doit être un entier.
, L m doit être un entier.
Pour une particule avec un spin S, cela prend en compte que la dépendance angulaire de l'emplacement de la particule, par exemple son orbite dans un atome. Il est par conséquent connu sous le nom moment angulaire orbital. Cependant, lorsque l'on fait tourner le système, on change aussi la essorage. Par conséquent, la moment cinétique total, qui est la pleine Générateur de rotations, est  Être un moment angulaire, J satisfait les mêmes relations de commutation que L, comme expliqué ci-dessous volonté. à savoir
Être un moment angulaire, J satisfait les mêmes relations de commutation que L, comme expliqué ci-dessous volonté. à savoir
à partir duquel suit
Agir avec J sur la fonction d'onde 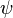 d'une particule génère une rotation:
d'une particule génère une rotation: 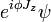 est le fonction d'onde
est le fonction d'onde 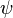 entraîné en rotation autour de l'axe z d'un angle
entraîné en rotation autour de l'axe z d'un angle  . Pour une rotation d'un angle infinitesmal
. Pour une rotation d'un angle infinitesmal  , La rotation fonction d'onde est
, La rotation fonction d'onde est  . Ceci est également vrai pour les rotations autour d'un axe quelconque.
. Ceci est également vrai pour les rotations autour d'un axe quelconque.
Dans une particule chargée l'élan obtient une contribution du champ électromagnétique et le moment cinétique L et J changements en conséquence.
Si le Hamiltonien est invariant par rotation, comme dans les problèmes à symétrie sphérique, puis en fonction de Théorème de Noether, il commute avec la moment cinétique total. Ainsi, le moment cinétique total est un quantité conservée
Depuis le moment angulaire est le générateur de rotations, les relations de commutation suivent les relations de commutation des générateurs de la tridimensionnel groupe de rotation SO (3). Ce est pourquoi J satisfait toujours ces relations de commutation. En d dimensions, le moment angulaire satisfera les mêmes relations de commutation que les générateurs du groupe de rotation de dimension d SO (d).
SO (3) a le même Algèbre de Lie (les mêmes relations de commutation) que SU (2). Générateurs de SU (2) peut avoir des demi-entiers valeurs propres , et ne peut donc m 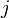 . En effet pour fermions la spin S et moment cinétique total J sont demi-entier. En fait, ce est le cas le plus général: j et m
. En effet pour fermions la spin S et moment cinétique total J sont demi-entier. En fait, ce est le cas le plus général: j et m 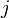 sont des nombres entiers ou demi-entiers.
sont des nombres entiers ou demi-entiers.
Techniquement, ce est parce que la revêtement universel de SO (3) est isomorphe SU (2), et le représentations de cette dernière sont entièrement connue. J i SPAN la Algèbre de Lie et J 2 est le Casimir invariant, et il peut être démontré que si les valeurs propres de J z et J 2 sont m j et j (j + 1) alors m j et j sont tous deux des multiples entiers de la moitié. j est non-négatif et m j prend des valeurs entre -j et j.
Rapport à harmoniques sphériques
Opérateurs de moment angulaire se produisent généralement lorsque la résolution d'un problème avec une symétrie sphérique en coordonnées sphériques . Puis, le moment angulaire dans la représentation de l'espace est:
Lors de la résolution de trouver états propres de cet opérateur, nous obtenons ce qui suit
où
sont les harmoniques sphériques.
Moment angulaire en électrodynamique
En décrivant le mouvement d'une particule chargée en présence d'un champ électromagnétique, le «moment cinétique" ne est pas p invariant de jauge. En conséquence, le moment cinétique canonique  invariant de jauge est pas non plus. Au lieu de cela, l'élan qui est physique, la soi-disant dynamique canonique, est
invariant de jauge est pas non plus. Au lieu de cela, l'élan qui est physique, la soi-disant dynamique canonique, est
où  est la charge électrique , c la vitesse de la lumière et de l'Un potentiel vecteur. Ainsi, par exemple, la Hamiltonien d'une particule chargée de masse m dans un champ électromagnétique est alors
est la charge électrique , c la vitesse de la lumière et de l'Un potentiel vecteur. Ainsi, par exemple, la Hamiltonien d'une particule chargée de masse m dans un champ électromagnétique est alors
où  est le potentiel scalaire. Ce est le hamiltonien qui donne le Droit de la force de Lorentz. La dynamique invariante de jauge angulaire, ou «moment angulaire cinétique» est donnée par
est le potentiel scalaire. Ce est le hamiltonien qui donne le Droit de la force de Lorentz. La dynamique invariante de jauge angulaire, ou «moment angulaire cinétique» est donnée par
L'interaction avec la mécanique quantique est discuté dans l'article sur relations de commutation canoniques.

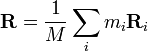
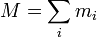


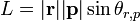

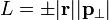
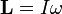

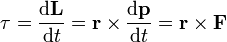
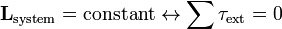


![\ Left [L_i, L ^ 2 \ right] = 0](../../images/635/63559.png)
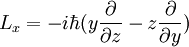
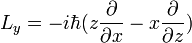

![\ Begin {align} \ left [L_x, L_y \ right] = & - \ hbar ^ 2 \ gauche ((y {\ \ partiel sur \ z partielle} - z {\ \ partiel sur \ y partielle}) (z { \ \ partiel sur \ x partielle} - {x \ \ partiel sur \ z partielle}) - (z {\ \ partiel sur \ x partielle} - {x \ \ partiel sur \ z partielle}) (y {\ partial \ over \ z partielle} - z {\ \ partiel sur \ y partielle}) \ right) = \\ & - \ hbar ^ 2 \ left (y {\ \ partiel sur \ x partielle} - {x \ \ partiel sur \ y partielle} \ right) = i \ HBAR L_z. \\ \ End {align}](../../images/635/63563.png)

![[J_ \ ell, J_m] = i \ hbar \ sum_n \ varepsilon_ {} lmn J_n](../../images/635/63575.png)
![\ Left [J_ \ ell, J ^ 2 \ right] = 0.](../../images/635/63576.png)
![\ Left [J_l, H \ right] = 0](../../images/635/63580.png)